文档内容
2024-2025 学年第一学期六校联合体 10 月联合调研
高三数学
2024.10.22
注意事项:
1.本试卷考试时间为120分钟,试卷满分150分,考试形式闭卷.
2.本试卷中所有试题必须作答在答题卡上规定的位置,否则不给分.
3.答题前,务必将自己的姓名、准考证号用 0.5 毫米黑色墨水签字笔填写在试卷及答题卡
上.
一、选择题:本题共 8小题,每小题 5分,共 40分.在每小题给出的四个选项
中,只有一项是符合题目要求的.
1.已知集合A={x| x2-2x-8<0},B={x| x≤4 },则“x∈A”是“x∈B”
A.充要条件 B.必要不充分条件
C.充分不必要条件 D.既不充分也不必要条件
-
2-i
2.若复数z满足z = ,则|z|=
3+i
5 10 2 1
A. B. C. D.
10 2 2 2
3.甲、乙、丙、丁去听同时举行的3个讲座,每人可自由选择听其中一个讲座,则恰好
只有甲、乙两人听同一个讲座的种数为
A.6 B.12 C. 18 D. 24
4.已知等比数列{a }满足a a a =64,则a a +a a 的最小值为
n 4 5 6 2 4 6 8
A.48 B.32 C.24 D.8
- 1 x3+ax2-a-4(x≥0)
5.已知函数 f(x)= 3 在R上单调,则实数a的取值范围为
ax-sinx(x<0)
A.(-∞,-1) B.(-∞,-1] C.[-4,-1) D.[-4,-1]
x2 y2
6.已知圆(x-2)2+y2=1与双曲线 - =1(a>0,b>0)的一条渐近线交于A,B两点,且
a2 b2
|AB|=1,则该双曲线的离心率为
2 13 4 13
A.2 B. 13 C. D.
13 13
7.已知函数f(x)=(x-4)3 cosωx(ω>0),存在常数a∈R,使f(x+a)为偶函数,则ω的最小
值为
π π π π
A.12 B.8 C.4 D. 2
8.已知 2024m=2025,2023m=x+2024 ,2025m=y+2026,则
A.0<x<y B.x<y<0 C.y<x<0 D.x<0<y
1
{#{QQABIQAAggCgAhBAAAhCQQ2ACkOQkhCCCSgOAAAIMAAASBFABAA=}#}二.多项选择题:本题共 3小题,每小题 6 分,共 18分.在每小题给出的选项中,
有多项符合题目要求.全部选对的得 6 分,部分选对的得部分分,有选错的得 0
分.
9.下列说法中正确的是
A.若随机变量X~B(10,p),且E(X)=3,则D(X)=2.1
B.某射击运动员在一次训练中10次射击成绩(单位:环)如下:6,5,7,9,6,8,9,
7,9,5,这组数据的75百分位数为7
1
C.若随机变量ξ~N(μ,σ2),且P(ξ>3)=P(ξ<-1)=p,则P(1≤ξ≤3)= -p
2
^ - - 4
D.若变量y关于变量x的线性回归方程为y=x+t,且x=4,y=2t,则t=
3
10.已知棱长为 4 的正方体 ABCD-A B C D ,球 O 是该正方体的内切球,E,F,P 分别
1 1 1 1
是棱AA ,BC,C D 的中点,M是正方形BCC B 的中心,则
1 1 1 1 1
π
A.球O与该正方体的表面积之比为
6
B.直线EF与OM所成的角的正切值为 2
C.直线EP被球O截得的线段的长度为2 2
D.球O的球面与平面APM的交线长为4π
11.已知函数 f(x)=x3+mx+1,则
A.当m=-1时,过点(2,2)可作3条直线与函数f(x)的图象相切
B.对任意实数m,函数 f(x)的图象都关于(0,1)对称
3
C.若f(x)存在极值点 x ,当 f(x )=f(x )且 x ≠x ,则 x + x =0
0 1 0 1 0 1 2 0
D.若有唯一正方形使其4个顶点都在函数f(x)的图象上,则m=-2 2
三、填空题:本题共 3 小题,每小题 5分,共 15 分.
12.已知向量a,b满足a+b=(2,1),a-b=(-2,4),则|a|-|b|=_______.
13.某个软件公司对软件进行升级, 将序列A=(a ,a ,a ,···)升级为新序列A*=(a -
1 2 3 2
a ,a -a ,a -a ,···), A*中的第n项为a -a , 若(A*)*的所有项都是3,且a =11,
1 3 2 4 3 n+1 n 4
a =18,则a =_______.
5 1
14.已知抛物线C:y2=4x的焦点为F,过点D(-1,0)的直线l在第一象限与C交于A,B
两点,且BF为∠AFD的平分线,则直线l的方程为_______.
2
{#{QQABIQAAggCgAhBAAAhCQQ2ACkOQkhCCCSgOAAAIMAAASBFABAA=}#}四、解答题:本题共 5 小题,共 77分.解答应写出文字说明、证明过程或演算步
骤.
15.(本题满分13分)
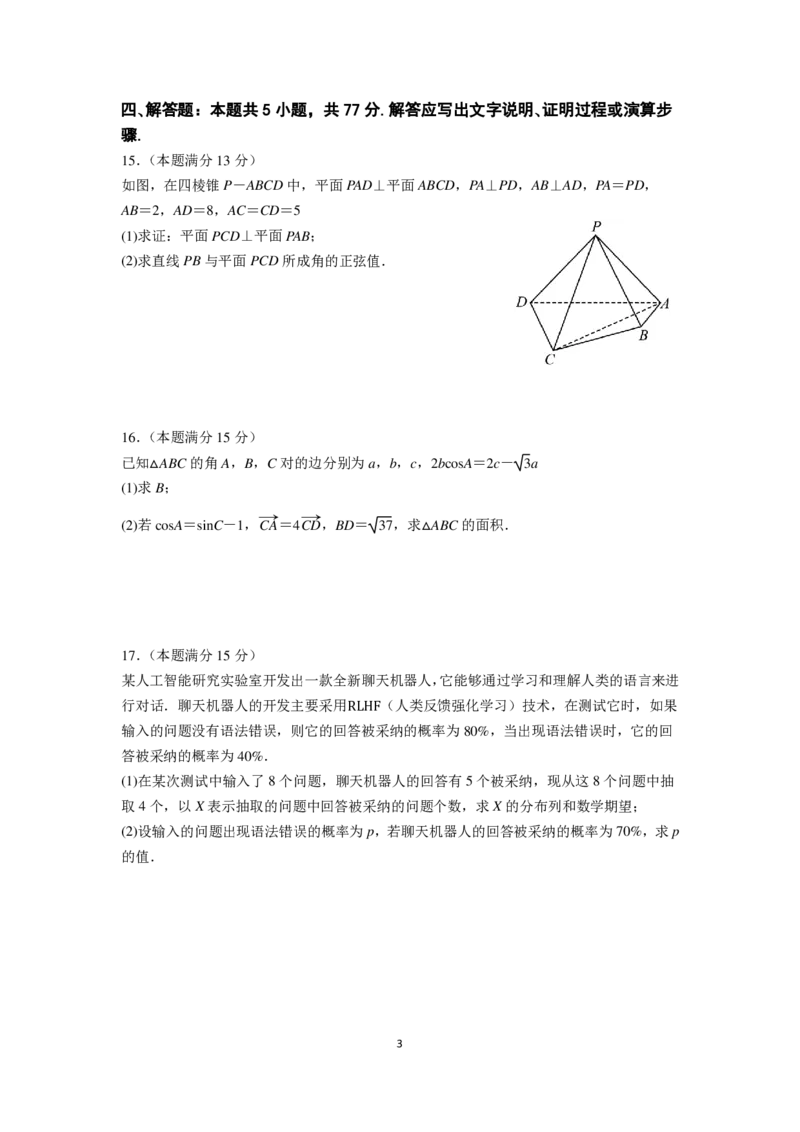
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,PA⊥PD,AB⊥AD,PA=PD,
AB=2,AD=8,AC=CD=5
(1)求证:平面PCD⊥平面PAB;
(2)求直线PB与平面PCD所成角的正弦值.
16.(本题满分15分)
已知△ABC的角A,B,C对的边分别为a,b,c,2bcosA=2c- 3a
(1)求B;
→ →
(2)若cosA=sinC-1,CA=4CD,BD= 37,求△ABC的面积.
17.(本题满分15分)
某人工智能研究实验室开发出一款全新聊天机器人,它能够通过学习和理解人类的语言来进
行对话.聊天机器人的开发主要采用RLHF(人类反馈强化学习)技术,在测试它时,如果
输入的问题没有语法错误,则它的回答被采纳的概率为80%,当出现语法错误时,它的回
答被采纳的概率为40%.
(1)在某次测试中输入了8个问题,聊天机器人的回答有5个被采纳,现从这8个问题中抽
取4个,以X表示抽取的问题中回答被采纳的问题个数,求X的分布列和数学期望;
(2)设输入的问题出现语法错误的概率为p,若聊天机器人的回答被采纳的概率为70%,求p
的值.
3
{#{QQABIQAAggCgAhBAAAhCQQ2ACkOQkhCCCSgOAAAIMAAASBFABAA=}#}18.(本题满分17分)
已知 f(x)=ln(x+1)
(1) 设h(x)=x f(x-1),求 h(x)的极值.
(2) 若 f(x)≤ax在[0,+∞)上恒成立,求a的取值范围.
(3) 若存在常数M,使得对任意x∈I,f(x)≤M恒成立,则称f(x)在I上有上界M,函数f(x)
称为有上界函数.如 y=ex是在 R 上没有上界的函数, y=lnx 是在(0,+∞)上没有上界的
1 1 1
函数;y=-ex,y=-x2都是在R上有上界的函数.若g(n)=1+ + +···+ (n∈N*),则
2 3 n
g(n)是否在N *上有上界? 若有,求出上界;若没有,给出证明.
19.(本题满分17分)
x2 y2
已知椭圆C: + =1(a>b>0),C的上顶点为B,左右顶点分别为A 、A ,左焦点为F ,
a2 b2 1 2 1
1
离心率为 .过F 作垂直于x轴的直线与C交于D,E两点,且| DE |=3.
2 1
(1)求C的方程;
(2)若M,N是C上任意两点
3
①若点M(1, ),点N位于x轴下方,直线MN交x轴于点G,设△MA G和△NA G
2 1 2
的面积分别为S ,S ,若2S -2S =3,求线段MN的长度;
1 2 1 2
②若直线MN与坐标轴不垂直,H为线段MN的中点,直线OH与C交于P,Q两点,
已知P,Q,M,N四点共圆, 求证:线段MN的长度不大于 14.
4
{#{QQABIQAAggCgAhBAAAhCQQ2ACkOQkhCCCSgOAAAIMAAASBFABAA=}#}