10月考_2024-2025高三（6-6月题库）_2024年10月试卷_1015四川省成都外国语学校2024-2025学年高三上学期10月月考_成都外国语学校高2022级高三上10月月考数学试题（含答案）

成都外国语学校高 2022 级十月月考 数学试卷 命题人：许桂兵 审题人：喻焰彬 注意事项： 1. 本试卷分第I卷（选择题）和第II卷（非选择题）两部分； 2. 本堂考试时间120分钟，满分150分； 3. 答题前考生务必先将自己的姓名、学号填写在答题卡上，并用2B铅笔填涂； 4. 考试结束后将答题卡交回。 第I卷（选择题部分，共 58 分） 一、单项选择题：本题共8个小题，每小题5分，共40分，在每小题给出的四个选项中只 有一项是符合题目要求的. 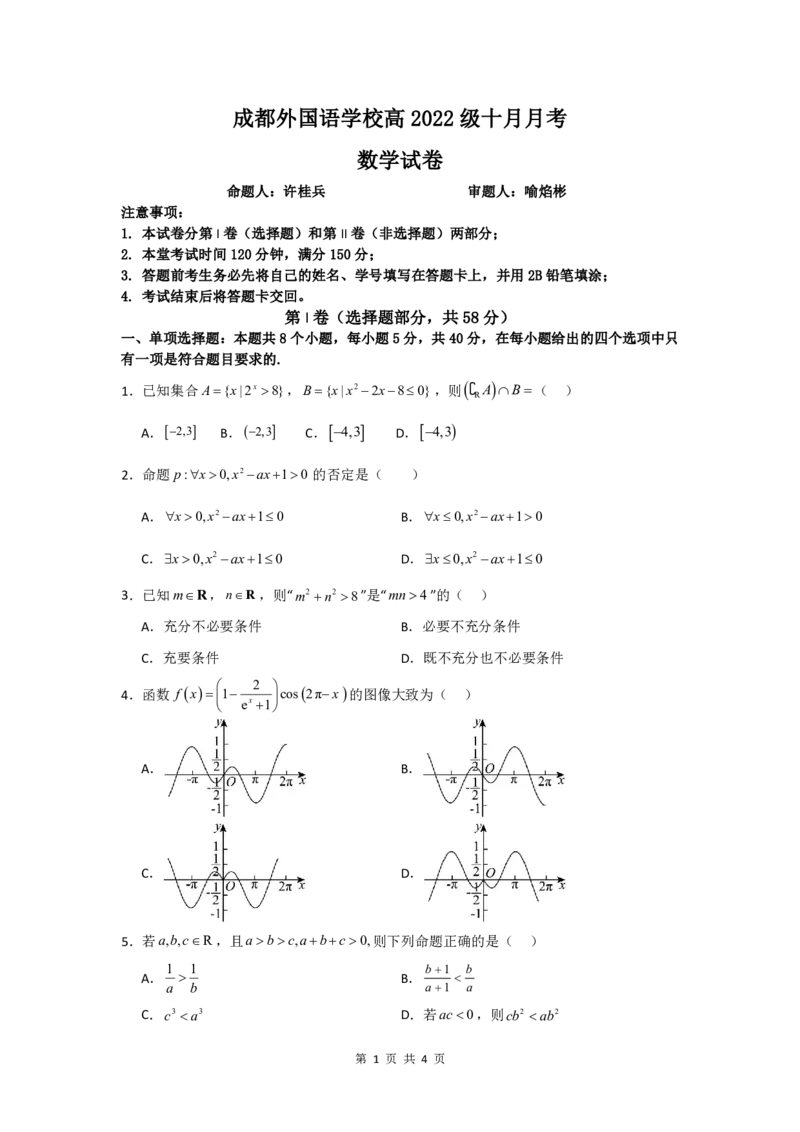1．已知集合A{x|2x 8}，B{x|x22x80}，则  ð A B（ ） R A．2,3 B．2,3 C．4,3  D．4,3 2．命题 p:x0,x2ax10 的否定是（ ） A．x0,x2ax10 B．x0,x2ax10 C．x0,x2ax10 D．x0,x2ax10 3．已知mR，nR，则“m2n2 8”是“mn4”的（ ） A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件  2  4．函数 f x1 cos2πx 的图像大致为（ ）  ex 1 A． B． C． D． 5．若a,b,cR，且abc,abc0,则下列命题正确的是（ ） 1 1 b1 b A．  B．  a b a1 a C．c3 a3 D．若ac0，则cb2 ab2 第 1 页 共 4 页 {#{QQABQQyAggAAAoAAAAgCQwG6CAGQkAEACQgGQBAIsAAACAFABCA=}#}6．下列说法正确的有是（ ） A.若函数 f(x)为奇函数，则 f(0)0； B.函数 f(x) 1 在(，1)  (1，)上是单调减函数； x1 1 C.若函数y f(2x1)的定义域为[2,3]，则函数 f(x)的定义域为[ ,1]； 2 1 D.将y f 2x的图像向右平移 个单位，可得y f 2x1的图像 2 7．已知定义在R上的函数 f(x)满足 f(x) f(2x)， f(x) f(x)0，且在(0,1]上有 x 1 f(x)  ，则 f(2020.5)（ ） 4 1 1 1 1 A． B． C． D． 16 16 4 2 8.定义min{p,q,r}表示 p，q，r中的最小值．已知实数a，b，c满足abc0，abc2， 则（ ） A．min{a,b,c}的最大值是2 B．min{a,b,c}的最大值是3 4 C．max{a,b,c}的最小值是2 D．max{a,b,c}的最小值是3 4 二、多项选择题：本题共3个小题，每小题6分，共18分.在每小题给出的四个选项中， 有多项符合题目要求；全部选对的得6分，部分选对得部分分，有选错的得0分. 9．已知正数x、y，满足x y2，则下列说法正确的是（ ） A．xy的最大值为1 B． x y 的最大值为2 2 1 x2 y2 C．  的最小值为2 2 D．  的最小值为1 x y x1 y1 10.函数 f(x)22x 2x12的定义域为M ，值域为[1,2]，下列结论中一定成立的结论的序号 是（ ） A．M (,1] B．M [2,1] C．1M D．0M 8 11.若2a1 3,2b  ，则以下 结论正确的有（ ） 3 1 1 3 A.ba>1 B.  2 C.ab D.b2 2a a b 4 第 2 页 共 4 页 {#{QQABQQyAggAAAoAAAAgCQwG6CAGQkAEACQgGQBAIsAAACAFABCA=}#}第II卷（非选择题部分，共 92分） 三、填空题:本题共3个小题，每小题5分，共15分. 4  1 7 12．计算( ) 2 ( )0 (2)2  . 9 6 13．已知函数 f(x) log (x1) ，若1ab，且 f(a) f(b)，则ab2的取值范围 2 是 . n 14.已知不等式xlnxmlnx xn对x0恒成立，则当 取最大值时，m________ m 四、解答题:本题共5个小题，共70分,其中15题13分，16、17题每题15分，18、19题 每题17分，解答应写出文字说明、证明过程或演算步骤. 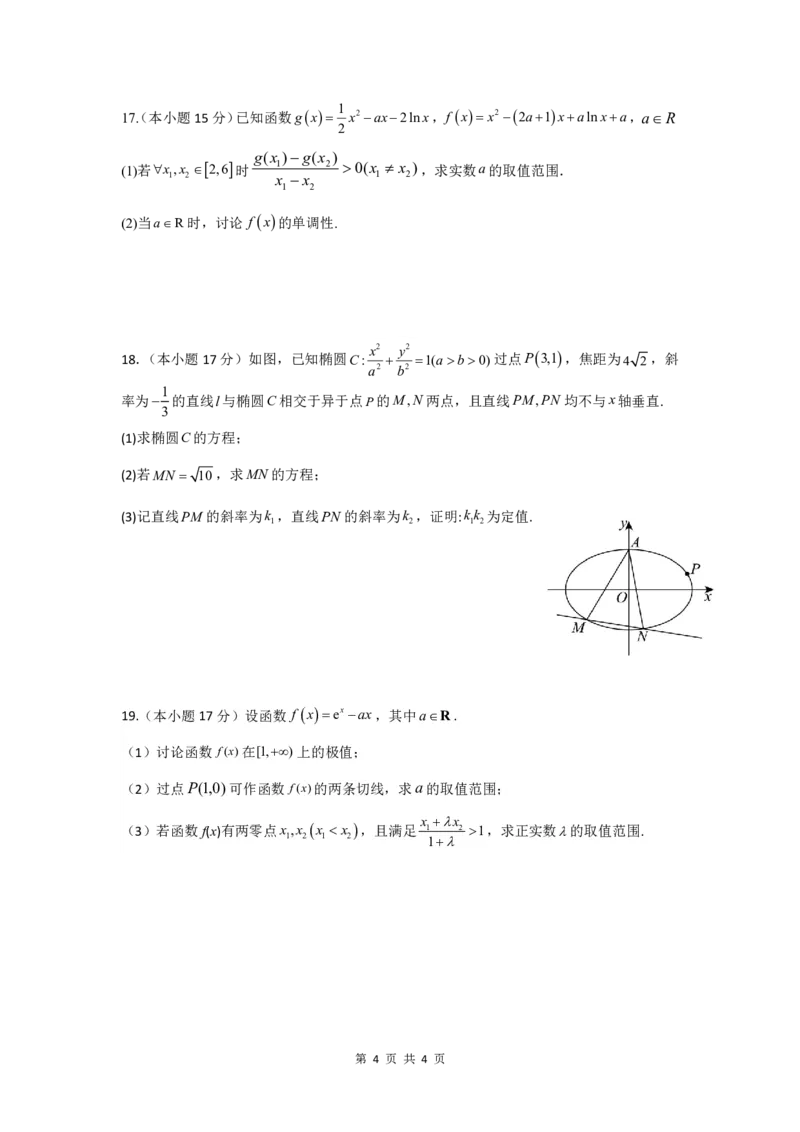15．（本小题13分）在VABC中，内角A，B，C的对边分别是a，b，c，且满足   bsinAacosB   6 (1)求B； (2)若b2，求VABC周长的取值范围． 16．（本小题15分）如图，在正三棱柱ABCABC 中，AB1,AA 4,D 是AA 中点，E在 1 1 1 1 1 棱BB 上，且BE3BE. 1 1 (1)求证：平面CDE 平面AACC； 1 1 1 (2)求平面CDE与平面ABC的夹角的余弦值. 1 第 3 页 共 4 页 {#{QQABQQyAggAAAoAAAAgCQwG6CAGQkAEACQgGQBAIsAAACAFABCA=}#}1 17（. 本小题15分）已知函数gx x2ax2lnx，f x x22a1xalnxa，aR 2 g(x )g(x ) (1)若x,x 2,6时 1 2 0(x  x )，求实数a的取值范围． 1 2 x x 1 2 1 2 (2)当aR时，讨论 f x的单调性. 18．（本小题17分）如图，已知椭圆C: x2  y2 1(ab0)过点P3,1，焦距为4 2，斜 a2 b2 1 率为 的直线l与椭圆C相交于异于点P的M,N两点，且直线PM,PN 均不与x轴垂直. 3 (1)求椭圆C的方程； (2)若MN  10，求MN的方程； (3)记直线PM 的斜率为k ，直线PN的斜率为k ，证明:kk 为定值. 1 2 1 2 19.（本小题17分）设函数 f xexax，其中aR. （1）讨论函数 f(x)在[1,)上的极值； （2）过点P(1,0)可作函数 f(x)的两条切线，求a的取值范围； x x （3）若函数f(x)有两零点x,x x x ，且满足 1 2 1，求正实数的取值范围. 1 2 1 2 1 第 4 页 共 4 页 {#{QQABQQyAggAAAoAAAAgCQwG6CAGQkAEACQgGQBAIsAAACAFABCA=}#}