10月考-答案_2024-2025高三（6-6月题库）_2024年10月试卷_1015四川省成都外国语学校2024-2025学年高三上学期10月月考_成都外国语学校高2022级高三上10月月考数学试题（含答案）

成都外国语学校高 2022 级十月月考数学参考答案 一．单选题：1.A 2. C 3.B 4.A 5.C 6.D 7.D 8.C 二．多选题：9.ABD 10.ACD 11.BC 1 三、填空题：12． ； 13．(2,)；14.e 2 四、解答题  π 15.（1）由正弦定理得sinBsinAsinAcosB ，  6  3 1  3 1 故sinBsinAsinA cosB sinB sinAcosB sinAsinB，    2 2  2 2 1 3 所以 sinBsinA sinAcosB ，…………………………3分 2 2 因为A0,π，sinA0， 1 3  π 所以 sinB cosBsin B  0， 2 2  3 π 因为B0,π，所以B ；………………………………6分 3 π （2）由（1）可知，B ，a2c2b2 ac， 3 又b2，所以a2c2 ac4，……………………………………8分 由基本不等式得：a2c2 2ac，即ac42ac， 所以ac4，当且仅当ac2时，等号成立. 又ac2 a2c22ac3ac416，…………………………10分 即0ac4，又acb2，所以2ac4， 所以4abc6， 即V ABC周长的取值范围是4,6  .………………………………13分 16．【详解】（1）设CD的中点为F ，过F 作GG ∥ AA分别交 1 1 1 AC,AC 于G,G ，连接EF、BG ，则G,G 分别为AC,AC 的中点， 1 1 1 1 1 1 1 1 1 所以FG  AD1， 1 2 1 由BB  AA 4,BE3BE，得BE1，即FG BE，又因为 1 1 1 1 1 1 第 1 页 共 5 页 {#{QQABQQyAggAAAoAAAAgCQwG6CAGQkAEACQgGQBAIsAAACAFABCA=}#}FG ∥BE， 1 1 所以四边形BEFG 是平行四边形， 1 1 所以EF ∥BG ，……………………………………………………………………3分 1 1 因为G 是AC 的中点，△ABC 为正三角形，所以BG  AC ， 1 1 1 1 1 1 1 1 1 1 由正三棱柱的性质得，AA 底面ABC ，且BG 底面ABC ， 1 1 1 1 1 1 1 1 1 所以BG  AA,AC AA  A，AC ,AA 平面AACC， 1 1 1 1 1 1 1 1 1 1 1 1 所以BG 平面AACC.………………………………………………………………6分 1 1 1 1 又因为EF ∥BG ，所以EF 平面AACC， 1 1 1 1 EF 平面CDE，所以平面CDE 平面AACC.……………………………………7分 1 1 1 1 （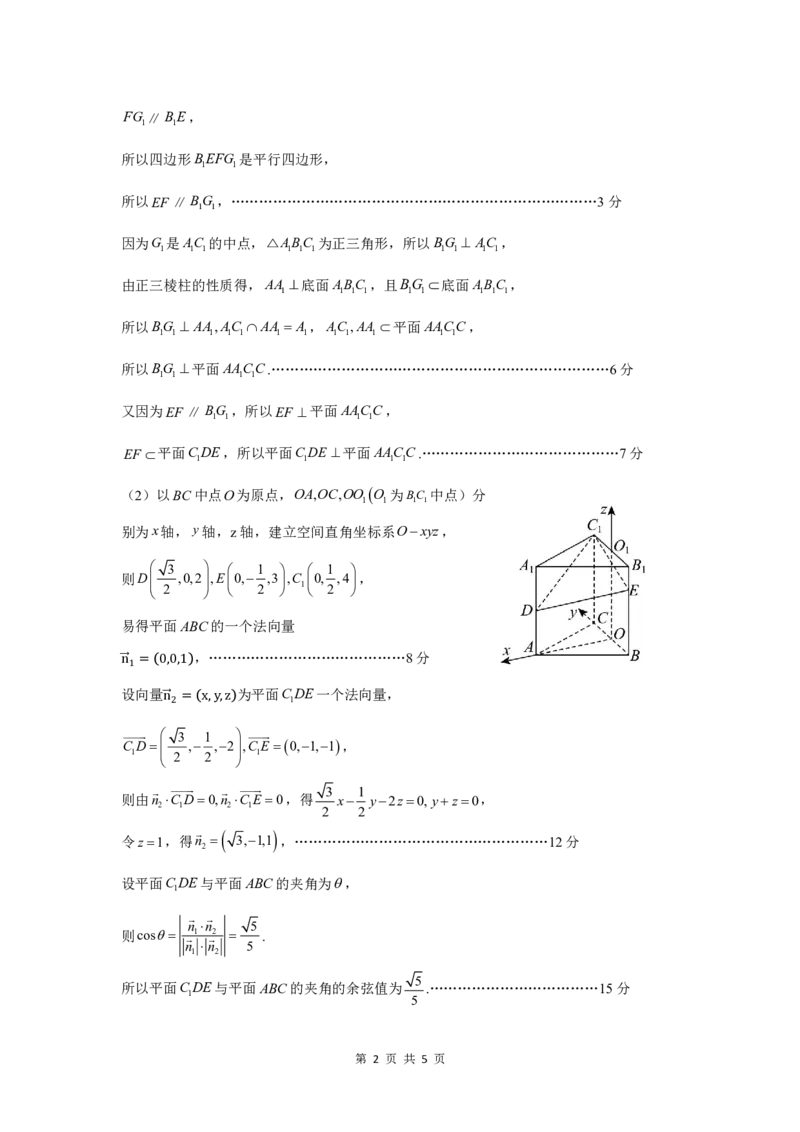2）以BC中点O为原点，OA,OC,OO O 为BC 中点）分 1 1 1 1 别为x轴，y轴，z轴，建立空间直角坐标系Oxyz，  3   1   1  则D   2 ,0,2   ,E  0, 2 ,3  ,C 1   0, 2 ,4  ， 易得平面ABC的一个法向量 ，……………………………………8分 n1 = 0,0,1 设向量 为平面CDE一个法向量， 1 n2 = x,y,z   3 1   CD , ,2,CE 0,1,1， 1   2 2   1     3 1 则由n CD0,n CE 0，得 x y2z0, yz0， 2 1 2 1 2 2    令z1，得n  3,1,1 ，………………………………………………12分 2 设平面CDE与平面ABC的夹角为， 1   n n 5 则cos  1  2  . n  n 5 1 2 5 所以平面CDE与平面ABC的夹角的余弦值为 .………………………………15分 1 5 第 2 页 共 5 页 {#{QQABQQyAggAAAoAAAAgCQwG6CAGQkAEACQgGQBAIsAAACAFABCA=}#}17.（1）依题意可得当x 2,6 时， ′ 恒成立， 所以xa 2 0在x 2,6 上恒成立 g ， x ≥0 x 即a x 2 在x 2,6 上恒成立，则a  x 2  .…………………………3分 x  x min 令hx x 2 ，x 2,6 ， x 由hx1 2 0，知hx在 2,6 上单调递增， x2 从而ahx h21. min 经检验知，当a1时，函数gx不是常函数， 所以a的取值范围是,1  .………………………………………………6分 （2） f x x22a1xalnxa，定义域为0,， fx2x2a1 a  2x1xa ，令 fx0，得x 1 或xa. x x 2  1 ①当a0时，当x0, 时， fx0， f x单调递减，  2 1  当x ,时， fx0， f x单调递增；…………………………………………8分 2  1 1  ②当0a 时，当x0,a和x ,时， fx0， f x单调递增， 2 2   1 当xa, 时， fx0， f x单调递减；…………………………………………10分  2 1 ③当a 时， fx0对x0,恒成立，所以 f x在0,单调递增；……12分 2 1  1 ④当a 时，当x0, 和xa,时， fx0， f x单调递增， 2  2 1  当x ,a时， fx0， f x单调递减.…………………………………………14分 2   1 1  综上所述：当a0时， f x在0, 单调递减，在 ,单调递增；  2 2  1  1 1  当0a 时， f x在a, 单调递减，在0,a和 ,单调递增； 2  2 2  1 当a 时， f x在0,单调递增； 2 1 1   1 当a 时， f x在 ,a单调递减，在0, 和a,单调递增.……………………15分 2 2   2 第 3 页 共 5 页 {#{QQABQQyAggAAAoAAAAgCQwG6CAGQkAEACQgGQBAIsAAACAFABCA=}#} 9 1  1  a2 b2 a2 3    18．【详解】（1）由题意得2c4 2 解得b2 ，    a2 b2c2 c2 2  x2 y2 故椭圆C的方程为  1.………………………………………………5分 12 4 1 （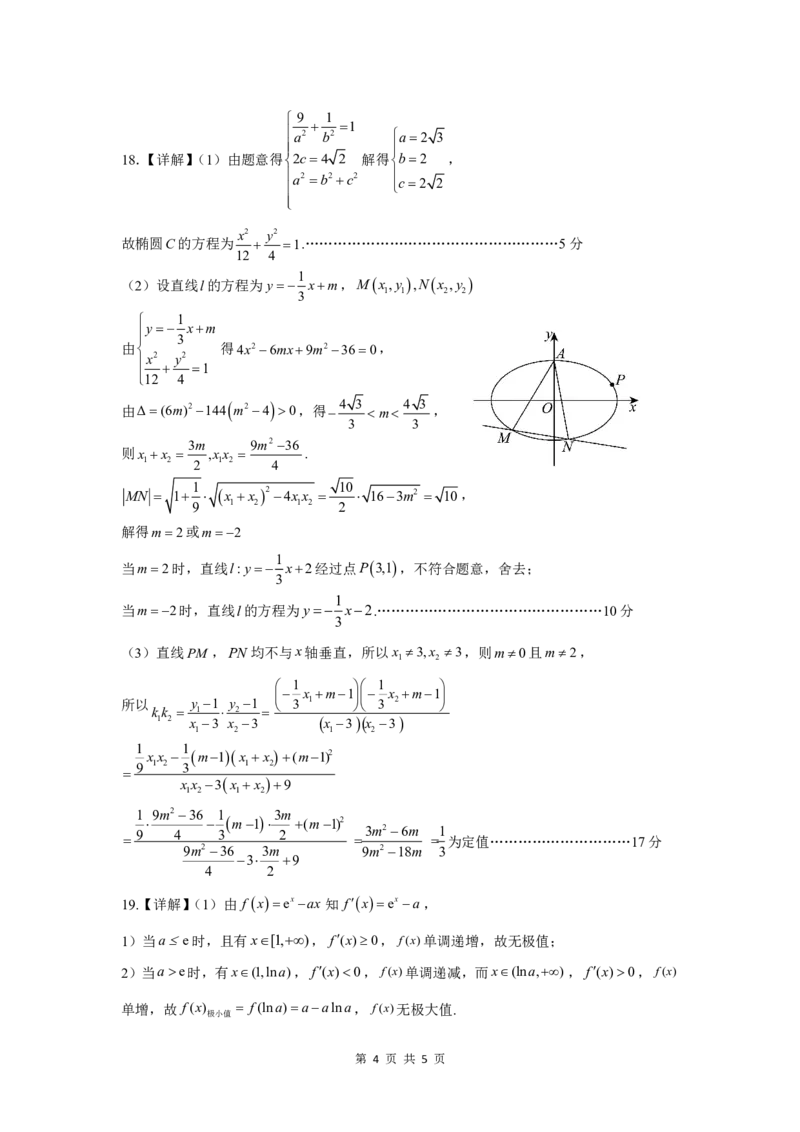2）设直线l的方程为y xm，Mx,y ,Nx ,y  1 1 2 2 3  1 y xm   3 由 得4x26mx9m2360， x2 y2  1 12 4 由Δ(6m)2144  m24  0，得 4 3  m 4 3 ， 3 3 3m 9m236 则x x  ,xx  . 1 2 2 1 2 4 1 10 MN  1  x x 24xx   163m2  10， 9 1 2 1 2 2 解得m2或m2 1 当m2时，直线l:y x2经过点P3,1，不符合题意，舍去； 3 1 当m2时，直线l的方程为y x2.…………………………………………10分 3 （3）直线PM ，PN均不与x轴垂直，所以x 3,x 3，则m0且m2， 1 2  1  1   x m1 x m1 所以 y 1 y 1  3 1  3 2  kk  1  2  1 2 x 3 x 3 x 3x 3 1 2 1 2 1 1 xx  m1x x  (m1)2 9 1 2 3 1 2  xx 3x x 9 1 2 1 2 1 9m236 1 3m   m1 (m1)2 9 4 3 2 3m26m 1    为定值…………………………17分 9m236 3m 9m218m 3 3 9 4 2 19.【详解】（1）由 f xexax 知 fxex a， 1）当ae时，且有x[1,)， f(x)0， f(x)单调递增，故无极值； 2）当ae时，有x(1,lna)，f(x)0，f(x)单调递减，而x(lna,)， f(x)0，f(x) 单增，故 f(x)  f(lna)aalna， f(x)无极大值. 极小值 第 4 页 共 5 页 {#{QQABQQyAggAAAoAAAAgCQwG6CAGQkAEACQgGQBAIsAAACAFABCA=}#}综上，当ae时， f(x)无极值； 当ae时， f(x)极小值为alna， f(x)无极大值；………………………………5分 （2）设点为Q(x ,ex 0 ax )为函数 f(x)图象上一点 0 0 则以点Q为切点的切线l方程为： y(ex 0 ax )(ex 0 a)(xx ) 0 0 又l过点P(1,0)则：0(ex 0 ax )(ex 0 a)(1x )即：a (2x )ex 0 0 0 0 令g(x )(2x )ex 0 ，则g(x )(1x )ex 0 0 0 0 0 当x 1时g(x )0，则g(x )当增；当x 1时g(x )0，则g(x )当减 0 0 0 0 0 0 g(x )  g(1)e 0 max x 时，g(x )；x 时，g(x )0 0 0 0 0 故0ae……………………………………………………………………11分 （3）由（1）可知当ae时， f(lna)a(1lna)0， f(0）10， 且x，（f x）， 由零点存在定理可知0 x lna x ，而题设可知ex1 ax ex2 ax 0，消去a可得 1 2 1 2 ex2 x x tlnt lnt ex2 x1  2 ，令t 2 1，且lntx x ，即x  ，x  ， …………14分 ex1 x x 2 1 2 t1 1 t1 1 1 x x (1)(t1) 将其代入 1 2 1，整理可令得F(t)lnt 0， 1 t1 1 (1)2  2t1  (t1) 而Ft   ， t (t1)2 t(t1)2 (t1)2 1)当1时，且t(1,)，有Ft 0，Ft单调递增，F(t)F(1)0，满足 t(t1)2 题设；  1  2)当01时，且t1, ，有F(t)0，Ft单调递减，F(t)F(1)0，不满足题设；  2  综上，的取值范围为[1,).…………………………………………………………17分 第 5 页 共 5 页 {#{QQABQQyAggAAAoAAAAgCQwG6CAGQkAEACQgGQBAIsAAACAFABCA=}#}