文档内容
兰州一中高三年级诊断考试试卷
高三数学
注意事项:
1.本试卷分第 I 卷(选择 )和第 II 卷(非选择题)两部分,满分150分,考试时间120分钟
2.答卷前,考生务必将自己的姓名、班级填写在答题卡上.
3.回答选择题时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号框涂黑.如需改动,用橡皮擦
干净后,再选涂其它答案标号框.回答非选择题时,将答案写在答题卡上,写在本试卷上无效.
第 I 卷(选择题
一、选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目
要求的.)
1.设全集 ,集合 满足 ,则( )
A. B. C. D.
={1,2,3,4,5} ∁ = 2,4
1⊆ 4⊆ 5∈ 3∉
2. “ ”是“ ”的( )
A. 充分不2 必要2 条件 2B. 必2 要不充分条件 C. 充要条件 D. 既不充分也不必要条件
( −1) + ⩽4 + ⩽1
3.已知向量 , , ,若 ,则实数 ( )
A. � �=(1,2) � �=B(.2,−2) � �=(1, ) C.� �⊥ (2� �+� �) D. =
1 1
4. 若复数2 满足 ,则复数 − 在复平面内对应的−点2位于( )
2 2
2024 2025
2+3i =i +8i �
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
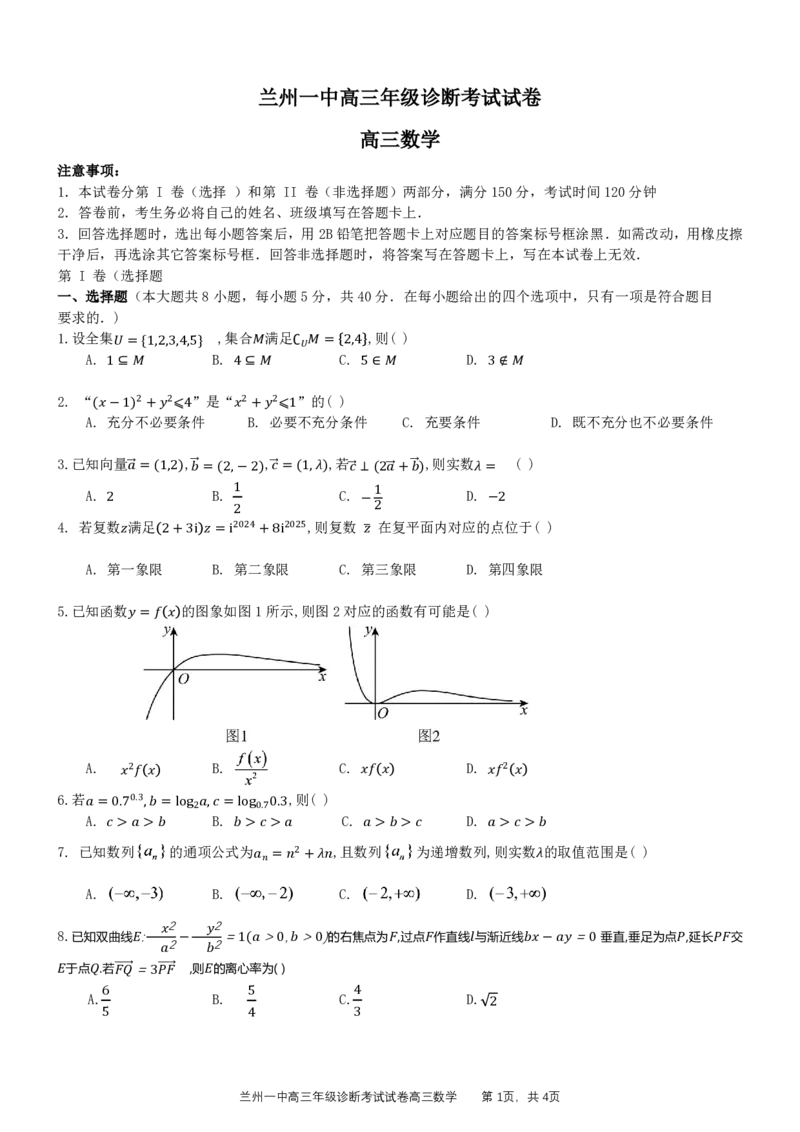
5.已知函数 的图象如图1所示,则图2对应的函数有可能是( )
=
A. B. C. D.
2 2
6.若 ,则( )
A. 0.3 B. C. D.
=0.7 , =log2 , =log0.70.3
7. 已知数 >列 > 的通项公式 为> > ,且数 列> > 为递增数列, 则>实 数> 的取值范围是( )
2
= +
A. B. C. D.
2 2
8.已知双曲线 : = > , > )的右焦点为 ,过点 作直线 与渐近线 = 垂直,垂足为点 ,延长 交
2 2
于点 .若 = −,则 的离心1(率 为(0) 0 − 0
A . ��� �� 3 ��� � B. C. D.
6 5 4
2
5 4 3
兰州一中高三年级诊断考试试卷高三数学 第1页,共4页
{#{QQABDYIEogigAIJAARgCQwUaCECQkAEACYgGBEAEsAAAwANABAA=}#}二、多选题(本大题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求,全部选
对得6分,部分选对得部分分,有选错的得0分.)
9.在下列函数中,最小值是 的是( )
A. 6 2 B.
2 2 1
= −4 + = −1+ 2 −1
C. D.
1 5 1
= −2 , ∈ (2,2 = +
10.已知 , 是两条不同的直线, , 是两个不同的平面,则下列说法正确的是( )
A. 若 , ,则 B. 若 , , ,则
⊥ ⊥ // ⊥ ⊥ ⊥ ⊥
C. 若 , , ,则 D. 若 , , ,则
// // // // // ⊥ ⊥ //
11.台球运动已有五、六百年的历史,参与者用球杆在台上击球.若和光线一样,台球在球台上碰到障碍物后也遵从
反射定律.如图,有一张长方形球台 ,其中 ,现从角落 沿角 的方向把球打出去,球经 次碰
3
撞球台内沿后进入角落 的球袋中, 则 的值 为 (=)5 2
A. B. C. D.
9 1 1 3
5 5 6 2
第 II 卷(非选择题)
三、填空题(本大题共3小题,每小题5分,共15分.)
12. 若命题“ , ”为假命题,则 的取值范围为.
2 2
∃ ∈ −1 + −1 −1⩾0
13. 若圆 与圆 有且仅有一条公切线,则 .
14. 一个不透明的袋子装有 个完全相同的小球,球上分别标有数字 , , , , .现甲从中随机摸出一个球记下
所标数字后放回,乙再从中随机摸出一个球记下所标数字,若摸出的球上所标数字大即获胜(若所标数字相同
5 1 2 3 4 4
则为平局),则在甲获胜的条件下,乙摸到 号球的概率为.
2
四、解答题(本大题共5小题,共77分.解答应写出必要的文字说明、证明过程或演算步骤。)
15. 在Δ 中,角 , , 的对边分别为 , , ,且 ,
Δ
.
2 2 2
(1)求ABC ; + − =24 ABC =12
(2)若 在边 上且 , ,求 的长.
=2 =2 5
兰州一中高三年级诊断考试试卷高三数学 第2页,共4页
{#{QQABDYIEogigAIJAARgCQwUaCECQkAEACYgGBEAEsAAAwANABAA=}#}16.函数 是定义在 上的奇函数,且当 时, .
2
>0 =− +2
(1)求函数 的解析式;
(2)若函数 在 上有三个零点,求 的取值范围.
= +
17.已知在四棱锥 中, 平面 ,四边形 是直角梯形, , ,若
, ,点 为 的中点,点 为 的四等分点(靠近点 ).
− ⊥ // ⊥
= =2 =2 2
(1)求证:平面 平面 ;
⊥
(2)求点 到平面 的距离.
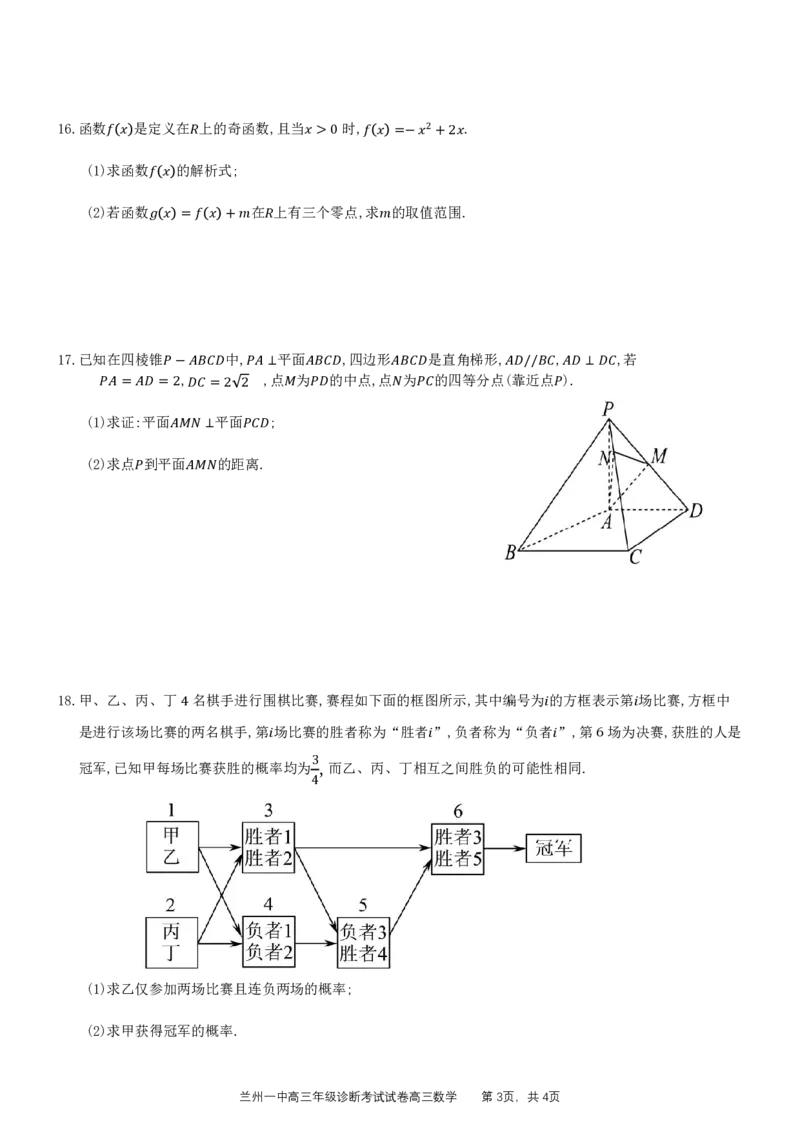
18.甲、乙、丙、丁 名棋手进行围棋比赛,赛程如下面的框图所示,其中编号为 的方框表示第 场比赛,方框中
是进行该场比赛的4两名棋手,第 场比赛的胜者称为“胜者 ”,负者称为“负者 ”,第 场为 决赛,获胜的人是
冠军,已知甲每场比赛获胜的概率 均为 ,而乙、丙、丁相互 之间胜负的可能性 相同. 6
3
4
(1)求乙仅参加两场比赛且连负两场的概率;
(2)求甲获得冠军的概率.
兰州一中高三年级诊断考试试卷高三数学 第3页,共4页
{#{QQABDYIEogigAIJAARgCQwUaCECQkAEACYgGBEAEsAAAwANABAA=}#}19.已知抛物线 ,过点 的直线与 交于 , 两点,设 在点 , 处的切线分别为 和 , 与 的交
点为 . 2
: = (1,2) 1 2 1 2
(1)若点 的坐标为 ,求Δ 的面积( 为坐标原点);
(−1,1) OAB
(2)证明:点 在定直线上.
兰州一中高三年级诊断考试试卷高三数学 第4页,共4页
{#{QQABDYIEogigAIJAARgCQwUaCECQkAEACYgGBEAEsAAAwANABAA=}#}