湖南省长沙市雅礼中学2023-2024学年高三下学期月考（八）数学试题+答案(1)_2024年4月_024月合集_2024届湖南长沙雅礼中学高三下学期月考（八）

炎德·英才大联考雅礼中学 2024 届高三月考试卷（八） 数学 命题人 李群丽 审题人 陈朝阳 注意事顶： 1．答卷前、考生务必将自己的姓名、考生号、考场号、座位号填写在答题卡上。 2．回答选择题时、选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。如需改 动、用橡皮擦干净后、再选涂其他答案标号。回答非选择题时，将答案写在答题卡上、写在 本试卷上无效。 3．考试结束后，将本试卷和答题卡一并交回。 一、选择题：本题共 8小题，每小题 5分，共40分、在每小题给出的四个选项中，只有一项 是符合题目要求的。 1．定义差集M N   x xM且xN  ，已知集合A 2,3,5  ,B 3,5,8 ，则A AB （ ） A． B． 2  C． 8  D． 3,5  1 2．已知一组数据x ,x ,x ,x ,x 的平均数为2，方差为 ，则另一组数据 1 2 3 4 5 2 3x 2,3x 2,3x 2,3x 2,3x 2 的平均数、标准差分别为（ ） 1 2 3 4 5 1 3 2 9 A．2, B．2,1 C．4, D．4, 2 2 2 3．设复数z满足 zi 2,z这在复平面内对应的点为P  x,y ，则（ ） A． x1 2  y2 4 B． x1 2  y2 2 C．x2  y1 2 2 D．x2  y1 2 4 4．向量的数量积可以表示为：以这组向量为邻边的平行四边形的“和对角线”与“差对角线”平方差的四分之   1  2  2  一，即如图所示，ab AD  BC ，我们称为极化恒等式、已知在△ABC中，M 是BC中点， 4   AM 3,BC 10，则ABAC （ ） A．16 B．16 C．8 D．8 5．南丁格尔玫瑰图是由近代护理学和护士教育创始人南丁格尔（FlorenceNightingale）设计的，图中每个扇 形圆心角都是相等的，半径长短表示数量大小，某机构统计了近几年中国知识付费用户数量（单位：亿人 次），并绘制成南丁格尔攻瑰图（如图所示）、根据此图，以下说法错误的是（ ） 学科网（北京）股份有限公司A．2015年至2022年，知识付费用户数量逐年增加 B．2015年至2022年，知识付费用户数量的逐年增加量在2018年最多 C．2015年至2022年，知识付费用户数量的逐年增加量逐年递增 D．2022年知识付费用户数量超过2015年知识付费用户数量的10倍 2  6．已知函数 f  x sin  2x (0)的图像关于点  ,0 中心对称，则（ ）  3  7 A．直线x  是函数 f  x 图象的对称轴 6   11 B． f  x 在区间   ,  上有两个极值点  12 12   5 C． f  x 在区间 0,  上单调递减  12   D．函数 f  x 的图象可由y cos2x向左平移 个单位长度得到 6 x2 y2 7．已知点O为坐标原点，椭圆  1的左、右焦点分别为F,F ，点P在椭圆上，设线段PF 的中 9 5 1 2 1 点为M ，且 OF  OM ，则△PFF 的面积为（ ） 2 1 2 15 A． 15 B． C．3 7 D．4 15 2 8．中国古建筑闻名于世，源远流长．如图甲所示的五脊殿是中国传统建筑中的一种屋顶形式，该屋顶的结 构示意图如图乙所示，在结构示意图中，已知四边形ABCD为矩形，EF∥AB,AB 2EF 4,△ADE与 △BCF都是边长为2的等边三角形，若点A,B,C,D,E,F 都在球O的球面上，则球O的表面积为（ ） 学科网（北京）股份有限公司11 11 A．22 B．11 C． D． 2 4 二、选择题：本题共 3小题，每小题 6分，共18分，在每小题给出的选项中，有多项符合题 目要求，全部选对的得6分，部分选对的得部分分，有选错的得 0分。 9．已知直线 2m1  x 1m  ym20  mR 与圆：x2  y2 4x 0，则下列结论正确的是（ ） A．对mR，直线恒过一定点 B．mR，使得直线与圆相切 C．对mR，直线与圆一定相交 D．直线与元相交且直线被圆所截得的最短弦长为2 2 10．已知△ABC满足sinA:sinB:sinC 2:3: 7 ，且△ABC的面积S 6 3，则下列命题正确的 △ABC 是（ ） A．△ABC的周长为5 7 B．△ABC的三个内角A、B、C满足关系AB2C 2 21 C．△ABC的外接圆半径为 3 19 D．△ABC的中线CD的长为 2 11．已知 f  x  xex,g  x  xlnx．若存在x R,x  0,，使得 f  x  g  x t 成立，则下列结 1 2 1 2 论正确的是（ ） 1 1 A．函数y  g  x 在  ,g  处的切线与函数 y f  x 在  1, f 1  处的切线吻合 e e B．当t 0时，x x t 1 2 C．当t 0时，elnt  x x 1 2 D．若 f  x  g  x mx恒成立，则m2 三、填空题：本题共 3小题，每小题 5分，共15分． 12．(13x)6的展开式中x3的系数为_________。  2 3 cos 13．若tan    ，则 _________。  3  5 sin 3cos 2n 14．已知数列 b 的通项公式为b n2cos ,T 是数列 b 的前n项和，则T _________。 n n 3 n n 3 n 四、解答题：本题共 5小题，共77分．请在答题卡指定区域内作答、解答时应写出文字说明、 学科网（北京）股份有限公司证明过程或演算步骤 15．（本小题满分13分） 已知函数 f  x  xk1  ex kR ． （1）当k 1时，求 f  x 在 0,2 处的切线方程 （2）讨论 f  x 在区间  0,3  上的最小值． 16．（本小题满分15分） 汽车尾气排放超标是全球变暖、海平面上升的重要因素．我国近几年着重强调可持续发展，加大在新能源 项目的支持力度，积极推动新能源汽车业发展，某汽车制造企业对某地区新能源汽车的销售情况进行调查， 得到下面的统计表： 年份t 2017 2018 2019 2020 2021 年份代码x  xt2016  1 2 3 1 5 销量 y/万辆 10 12 17 20 26 （1）统计表明销量 y 与年份代码x有较强的线性相关关系，求y 关于x的经验回归方程，并预测该地区新 能源汽车的销量最早在哪一年能突破50万辆； （2）某新能源汽车品牌销售商为了促销，采取“摸球定价格”的优惠方式，其规则为：盒子内装有编号为1， 2，3的三个相同的小球，有放回地摸三次，三次摸到相同编号的享受七折优惠，三次中仅有两次摸到相同 编号的享受八折优惠，其余情况均享受九折优惠，已知此款新能源汽车一台标价为100000元，设小李购买 此款新能源汽车的价格为X ，求X 的分布列与均值． n x y nxy 附： yb  xa 为经验回归方程，b   i1 i i ,a  yb  x ． n x2 nx2 i i1 17．（本小题满分15分） 如图，在四棱锥SABCD中，四边形ABCD是矩形，△SAD是正三角形，且平面SAD平面 2 3 ABCD,AB 1,P为梭AD的中点，四棱锥SABCD的体积为 ． 3 （1）若E为棱SB的中点，求证：PE∥平面SCD； 学科网（北京）股份有限公司2 3 （2）在棱SA上是否存在点M ，使得平面PMB与平面SAD所成夹角的余弦值为 ?若存在．求出线段 5 AM 的长度；若不存在，请说明理由． 18．（本小题满分17分） x2 y2 已知双曲线C:  1(a 0,b0)的右顶点E  1,0 ，它的一条渐近线的倾斜角为120． a2 b2 （1）求双曲线C的方程； （2）过点（2,0)作直线l交双曲线C于M,N 两点（不与点E重合），求证：EM EN ； （3）若过双曲线C上一点P作直线与两条渐近线相交，交点为A,B，且分别在第一象限和第四象限，若   1  AP PB, ,2 ，求△AOB面积的取值范围．   3  19．（本小题满分17分） 已知数列A:a ,a ,,a 为有穷正整数数列．若数列A满足如下两个性质，则称数列A为m的k减数列： 1 2 n ①a a a m ； 1 2 n ②对于1i j n，使得a a 的正整数对 i, j 有k个． i j （1）写出所有4的1减数列； （2）若存在m的6减数列，证明：m6； （3）若存在2024的k减数列，求k的最大值． 炎德·英才大联考雅礼中学 2024 届高三月考试卷（八） 数学参考答案 一、二、选择题 题号 1 2 3 4 5 6 7 8 9 10 11 答案 B C D A C C A A ACD BC ABC 1．B【解析】因为A 2,3,5  ,B 3,5,8 ，所以AB 3,5 ，所以A AB  2 ．故选B． 1 2．C【解析】因为一组数据x ,x ,x ,x ,x 的平均数为2，方差为 ，所以另一组数据3x 2,3x 2,3x 2， 1 2 3 4 5 2 1 2 3 1 9 3 2 3x 2,3x 2的平均数为3224，方差为32  ．平均数、标准差分别为4, ．故选C． 4 5 2 2 2 3．D     1     1 4．A【解析】由题设， AM 3, BC 10,ABAC   4 AM |2  BC|2   36100 16．故选 4 4 A． 学科网（北京）股份有限公司5．C【解析】对于A，由图可知，2015年至2022年，知识付费用户数量逐年增加，故A说法正确； 对于B和C，知识付费用户数量的逐年增加量分别为：2016年，0.960.480.48； 2017年，1.880.960.92;2018年，2.951.881.07; 2019年，3.562.950.61;2020年，4.153.560.59； 2021年，4.774.150.62;2022年，5.274.770.5； 则知识付费用户数量逐年增加量2018年最多，知识付费用户数量的逐年增加量不是逐年递增，故B说法正 确，C说法错误； 对于D，由5.27100.48，则2022年知识付费用户数量超过2015年知识付费用户数量的10倍，故D 说法正确．综上，说法错误的选项为C．故选C． 2   2  6．C【解析】因为函数 f  x 的图象关于点  ,0 中心对称，所以sin2   0，  3   3  4 2  2 可得 k kZ ，结合0，得 ，所以 f  x sin2x  ． 3 3  3  7  7 2 7 对于A，f   sin2   sin30，所以直线x  不是函数 f  x 图象的对称轴，故A  6   6 3  6 不正确；   11 2  5   11 对于B，当x   ,  时，2x   ,  ，所以函数 f  x 在区间   ,  上只有一个极  12 12  3  2 2   12 12  值点，故B不正确；  5 2 2 3  5 对于C当x 0,  时，2x   ,  ，所以函数 f  x 在区间 0,  上单调递减，故C正确；  12  3  3 2   12     对于D，y cos2x左移 个单位长度后得到 y cos2x  ，故D错误．故选C． 6  3  7．A【解析】由题意可得a 3,b 5,c 95 2． 如图，因为O,M 分别是FF 和PF 的中点，所以 PF 2OM 2OF 2c4，根据椭圆定义，可得 1 2 1 2 2 PF 2a2c2，又因为 FF 2c4， 1 1 2 PF 2  FF 2  PF 2 16164 7 所以cosPF F  2 1 2 1   ， 2 1 2 PF  FF 244 8 2 1 2 15 所以sinPF F  1cos2PF F  ， 2 1 2 1 8 学科网（北京）股份有限公司1 故△PFF 的面积为 PF  FF sinPF F  15．故选A． 1 2 2 2 1 2 2 1 另法：此题用等腰三角形求高或海伦公式更快捷． 8．A【解析】如图，根据球的性质可得OO 平面ABCD，根据中位线的性质和勾股定理可得MO  PQ 1 1 且MO  2 ，分类讨论当O在线段OM 上和O在线段MO 的延长线上时，由球的性质可得球半径的平 1 1 1 11 方为R2  ，再用球的表面积公式计算即可． 2 如图，连接AC,BD， 设ACBD O ，因为四边形ABCD为矩形，所以O 为矩形ABCD外接圆的圆心．连接OO ，则OO  1 1 1 1 平面ABCD，分别取EF,AD,BC的中点M,P,Q， 根据几何体ABCDEF 的对称性可知，直线OO 交EF 于点M ． 1 连接PQ，则PQ∥AB，且O 为PQ的中点， 1 因为EF∥AB，所以PQ∥EF ，连接EP,FQ， 在△ADE与△BCF，易知EP  FQ  2212  3 ，所以梯形EFQP为等腰梯形，所以MO  PQ， 1 42 2 且MO  ( 3)2    2 ． 1  2  设OO m，球O的半径为R，连接OE,OA， 1 当O在线段OM 上时，由球的性质可知R2 OE2 OA2，易得O A 22 12  5， 1 1 则( 2m)2 12 ( 5)2 m2，此时无解． 2 当O在线段MO 的延长线上时，由球的性质可知，( 5)2 m2 ( 2m)2 12，解得m ， 1 2 11 所以R2 OE2  ，所以球O的表面积S 4R2 22．故选A． 2 学科网（北京）股份有限公司2x y10, x1, 9．ACD【解析】由题设m  2xy1 x y20，令  x y20 y1, 所以直线 2m1  x 1m  ym20  mR 恒过定点 1,1 ，A对； 又x2  y2 4x 0的标准方程为(x2)2  y2 4 ，显然(12)2 12 24， 所以点 1,1 在圆x2  y2 4x 0内，故直线与圆必相交，B错，C对；要使直线与圆相交弦长最短，只需 定点 1,1 与圆心 2,0 的连线与已知直线垂直，此时定点与直线距离为 (12)2 (10)2  2 ，又圆的 半径为2，则最短相交弦长为2 22 ( 2)2 2 2 ，D对．故选ACD． 10．BC【解析】因为△ABC满足sin A:sinB:sinC 2:3: 7 所以a:b:c 2:3: 7 ， 设a 2t,b3t,c 7t,t 0， a2 b2 c2 4t2 9t2 7t2 1 利用余弦定理cosC    ， 2ab 12t2 2  由于C 0,，所以C  ． 3 对于A，因为S 6 3， △ABC 1 1 3 所以 absinC  2t3t 6 3，解得t 2． 2 2 2 所以a 4,b6,c2 7 ， 所以△ABC的周长为102 7，故A不正确；  2 对于B，因为C  ，所以AB ，故AB2C，故B正确； 3 3 7 2 21 对于C，由正弦定理得外接圆半径为  ，故C正确； sin60 3 对于D，如图所示， 学科网（北京）股份有限公司7 2 21 在△ABC中，利用正弦定理  ，解得sinA ， 3 sinA 7 2 2 7 又ac，所以cosA ， 7 在△ACD中，利用余弦定理CD2  AC2  AD2 2ACADcosA19，解得CD 19，故D不正确．故 选BC． 11．ABC【解析】选项A，由 f x ex x1  ,g x lnx10， 1 1 1 得 f1  g   0，又验证知 f 1  g   ， e e e 1 切线方程都为 y  ，故A正确； e 选项B， f  x  g  x t,t  xer 1  x lnx  lnx elnx 2 0， 1 2 1 2 2 2 则x 0,x 0,lnx 0，且t  f  x  f  lnx 0， 1 2 2 1 2 由 f  x  xex，得 f x ex x1 ， 当x0时， f x 0，则 f  x 在 0,上递增， 所以当t 0时， f  x t有唯一解，故x lnx ， 1 2 x x  x lnx t ，故B正确； 1 2 2 2 lnt lnt 选项C，由B正确，得  (t 0)， x x t 1 2 lnt 1lnt 设 t  ，则 t  ， t t2 令 t 0，解得t e， 易知 t 在 0,e  上单调递增，在  e,上单调递减， 学科网（北京）股份有限公司1 lnt 1  t  e  ,  ,elnt  x x ，故C正确； e x x e 1 2 1 2 选项D，由x0, f  x  g  x mx恒成立，即ex lnxm恒成立， 1 令r  x ex lnx，则r x ex  ， x 1 由r x 在 0,上递增，又r    e 20,r 1 e10， 2 1  存在x   ,1 ，使r x 0， 0 2  0 1 r  x 在 0,x 上递减，在 x ,上递增（其中x 满足ex 0  ，即x lnx ）． 0 0 0 x 0 0 0 1 r  x r  x ex 0 lnx  x 2， 0 0 x 0 0 要使mex lnx恒成立，mr  x ，存在2mr  x 满足题意，故D错误． 0 0 故选ABC． 三、填空题：本题共 3小题，每小题 5分，共15分． 12．540 2 3  2 tan 3 3 3 13． 【解析】依题意，tan     ，解得tan ， 3  3  1 3tan 5 2 cos 1 2 3 故   . sin 3cos tan 3 3 9n2 4n 2n 14． 【解析】因为b n2cos ， 2 n 3  4  2 设c b b b (3k2)2cos2k  (3k1)2cos2k  (3k)2cos2k k 3k2 3k1 3k  3   3  1  1 5  (3k2)2     (3k1)2 (3k)2 9k 2  2 2 所以T c c c c 3 1 2 3 n  5  5  5  5  9   92   93   9n   2  2  2  2 学科网（北京）股份有限公司5 9 123n  n 2 n  1n  5 9n2 4n 9  n 2 2 2 四、解答题：本题共 5小题，共77分．请在答题卡指定区域内作答．解答时应写出文字说明、 证明过程或演算步骤． 15．【解析】（1）当k 1时， f  x  x2  ex  f x  x1  ex, f 0 1， 所以k 1时，函数 f  x 在 0,2 处的切线方程为x y20． （2） f  x  xk1  ex  f x  xk  ex． 当xk时， f x 0，此时 f  x 单调递增；当xk时， f x 0，此时 f  x 单调递减， 当k 3时，函数在  0,3  上单调递减，故函数的最小值为： f(x)  f  3  2k  e3； min 当k 0时，函数在  0,3  上单调递增，故函数的最小值为： f(x)  f  0 1k； min 当0k 3时，函数的最小值为： f(x)  f  k ek． min 1k,k 0,  故 f(x) ek,0k 3, min  2k  e3,k 3.  12345 n 16．【解析】（1）由题意得x 3,x y 110212317420526295， 5 i1 i i 1012172026 n y  17,x2 12 22 32 42 52 55． 5 i1 i n x y nxy i i 2955317 所以b ˆ i1   4,aˆ y b ˆx 17 43 5.． n 5545 x2 nx2 i i1 所以 y关于x的经验回归方程为 y 4x5，令 y 4x550，得x11.25， 所以最小的整数为12,2016122028， 所以该地区新能源汽车的销量最早在2028年能突破50万辆． 1 （2）有放回地摸球，每次摸到某个编号的概率为 ， 3 3 1 1 则三次摸到相同编号的概率为3    ； 3 9 学科网（北京）股份有限公司1 1 2 2 三次中仅有两次摸到相同编号的概率为33    ； 5 5 2 5 X 70000 80000 90000 1 2 2 P 9 3 9 1 2 2 730000 故E  X 70000 80000 90000  ． 9 3 9 9 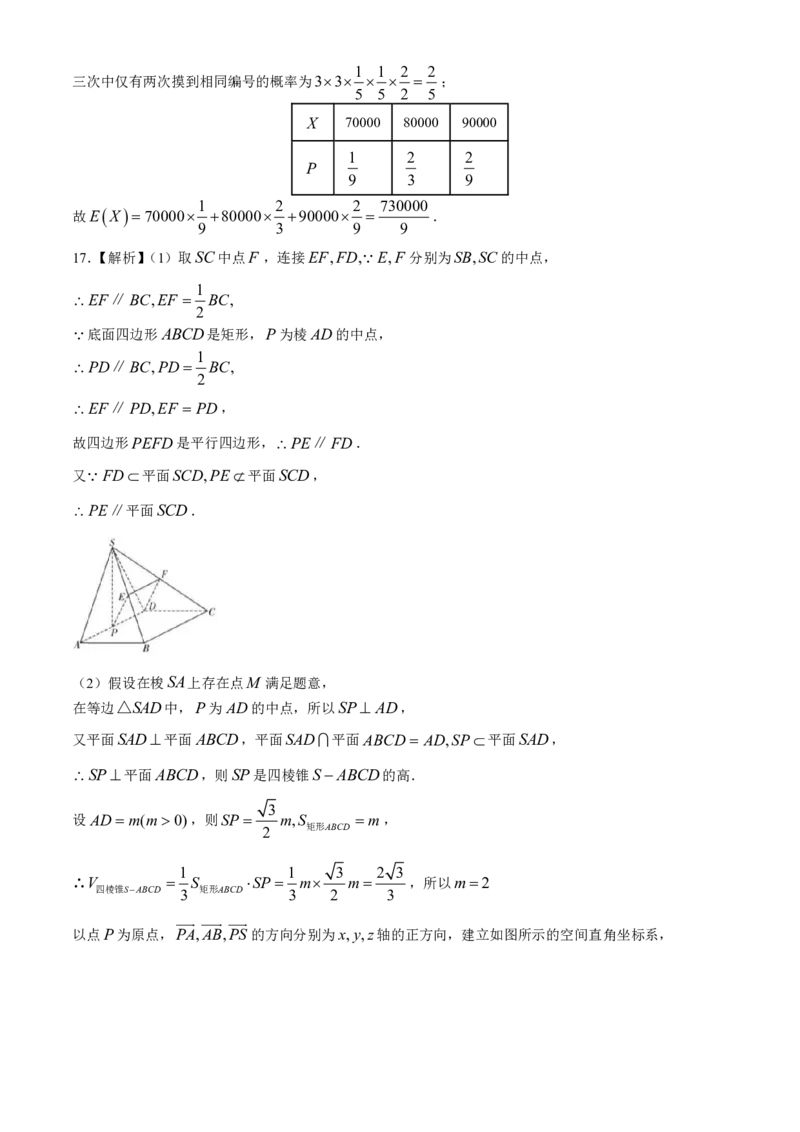17．【解析】（1）取SC中点F ，连接EF,FD,E,F 分别为SB,SC的中点， 1 EF∥BC,EF  BC, 2 底面四边形ABCD是矩形，P为棱AD的中点， 1 PD∥BC,PD  BC, 2 EF∥PD,EF  PD， 故四边形PEFD是平行四边形，PE∥FD． 又FD平面SCD,PE 平面SCD， PE∥平面SCD． （2）假设在梭SA上存在点M 满足题意， 在等边△SAD中，P为AD的中点，所以SP AD， 又平面SAD平面ABCD，平面SAD平面ABCD  AD,SP平面SAD， SP平面ABCD，则SP是四棱锥SABCD的高． 3 设AD m(m0)，则SP  m,S m， 2 矩形ABCD 1 1 3 2 3 ∴V  S SP  m m ，所以m2 四棱锥SABCD 3 矩形ABCD 3 2 3    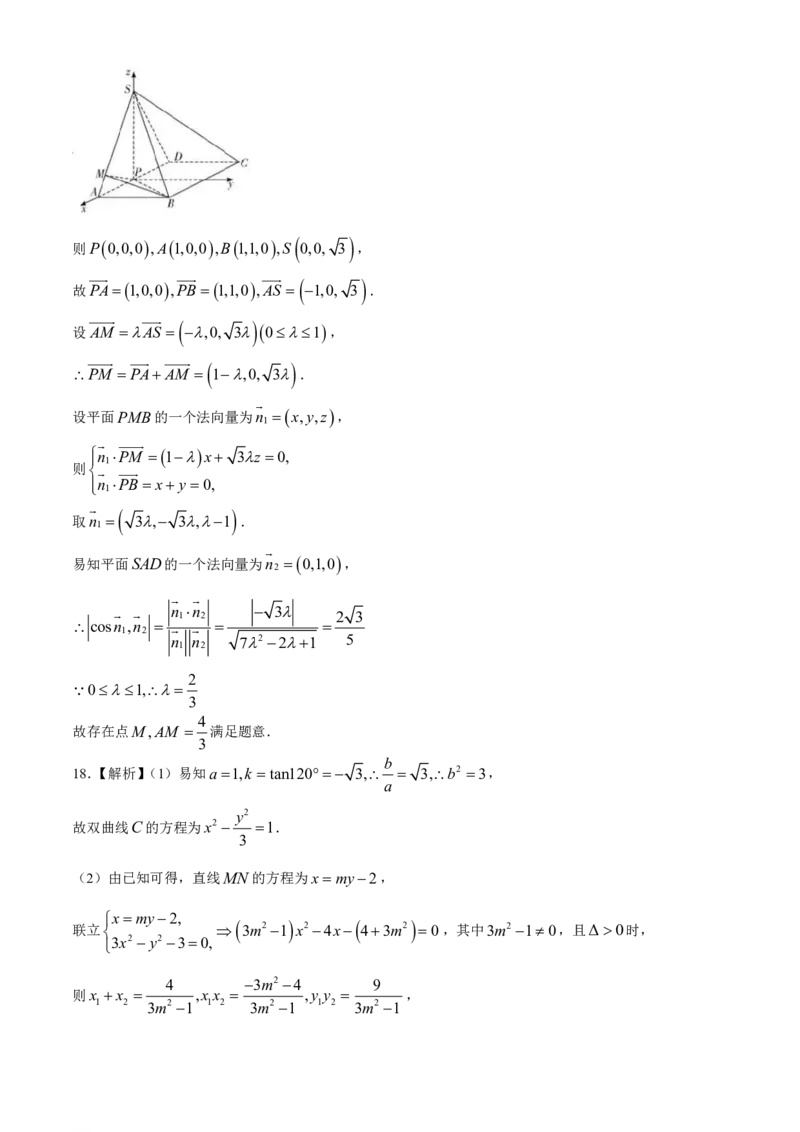以点P为原点，PA,AB,PS 的方向分别为x,y,z轴的正方向，建立如图所示的空间直角坐标系， 学科网（北京）股份有限公司  则P  0,0,0  ,A  1,0,0  ,B  1,1,0  ,S 0,0, 3 ，      故PA 1,0,0  ,PB   1,1,0  ,AS  1,0, 3 ．     设AM AS  ,0, 3  01 ，      PM  PA AM  1,0, 3 ．  设平面PMB的一个法向量为n  x,y,z ， 1    n PM  1 x 3z 0, 1 则  n 1 PB  x y  0,    取n  3, 3,1 ． 1  易知平面SAD的一个法向量为n  0,1,0 ， 2     n 1 n 2  3 2 3 cosn 1 ,n 2      n n 72 21 5 1 2 2 01, 3 4 故存在点M,AM  满足题意． 3 b 18．【解析】（1）易知a 1,k  tan120 3,  3,b2 3， a y2 故双曲线C的方程为x2  1． 3 （2）由已知可得，直线MN的方程为x my2， xmy2, 联立   3m21  x24x  43m2 0，其中3m2 10，且Δ0时， 3x2  y2 30, 4 3m2 4 9 则x x  ,x x  ,y y  ， 1 2 3m2 1 1 2 3m2 1 1 2 3m2 1 学科网（北京）股份有限公司  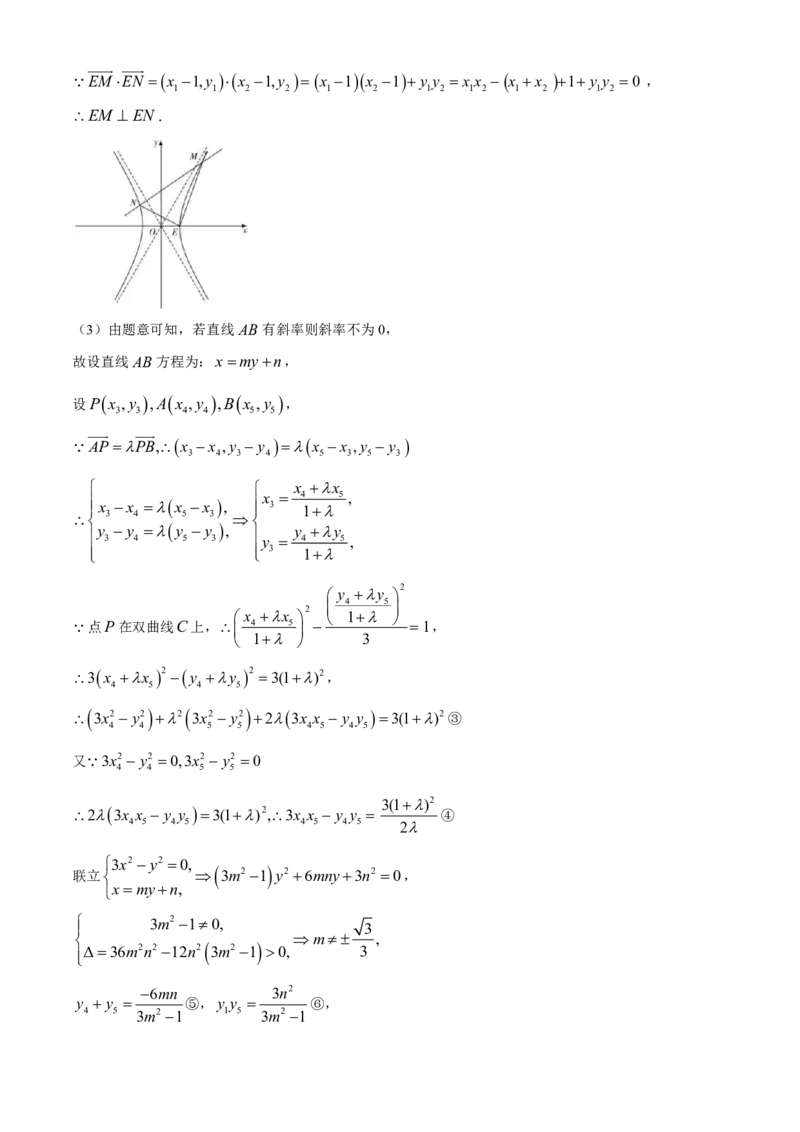EM EN  x 1,y  x 1,y   x 1  x 1  y y  x x   x x 1 y y 0 ， 1 1 2 2 1 2 1 2 1 2 1 2 1 2 EM EN． （3）由题意可知，若直线AB 有斜率则斜率不为0， 故设直线AB方程为：xmyn， 设P  x ,y  ,A  x ,y  ,B  x ,y ， 3 3 4 4 5 5   AP PB, x x ,y  y  x x ,y  y  3 4 3 4 5 3 5 3   x x  x x  x x  ,   x 3  4 1 5 ,  3 4 5 3  y  y  y  y  , y y   3 4 5 3 y  4 5 ,   3 1  y y  2 4 5  x x  2   1   点P在双曲线C上，  4 5   1，  1  3 3  x x 2  y y 2 3(1)2， 4 5 4 5   3x2  y2  2  3x2  y2  2 3x x  y y 3(1)2③ 4 4 5 5 4 5 4 5 又3x2  y2 0,3x2  y2 0 4 4 5 5 3(1)2 2 3x x  y y 3(1)2,3x x  y y  ④ 4 5 4 5 4 5 4 5 2 3x2  y2 0, 联立   3m2 1  y2 6mny3n2 0， xmyn,   3m2 10, 3  m ,  Δ36m2n2 12n2 3m2 1  0, 3 6mn 3n2 y  y  ⑤， y y  ⑥， 4 5 3m2 1 1 5 3m2 1 学科网（北京）股份有限公司A,B分别在第一象限和第四象限，y y 0,3m2 10， 4 5 3(1)2 由④式得：3  my n  my n y y  ， 4 5 4 5 2   3m21  y y 3mn  y  y 3n2  3(1)2 ⑦ 4 5 4 5 2 将⑤⑥代入⑦得：  3m2 1   3n2 3mn 6mn 3n2  3(1)2 ， 3m2 1 3m2 1 2 6n2 3(1)2   , 3m2 1 2 1 3 2 3 2 3 S  OA  OB sinAOB    y   y △AOB 2 4 3 4 3 5 3 3 3n2 n2  y y   3 3 4 5 3 3m2 1 3m2 1 1 3(1)2 3  1       2 2 3 2 4 3   1 1  令h  , ,2    3  1  由对勾函数性质可得h 在 ,1 上单调递减，在 1,2  上单调递增   3   10  4 3 h    2, 3   ,S △AOB   3, 3   . 19．【解析】（1）由题意得a a a  4，则1124或134， 1 2 n 故所有4的1减数列有数列1,2,1和数列3，1． （2）因为对于1i j n，使得a a 的正整数对 i, j 有k个， i j 且存在m的6减数列，所以C2 6，得n4． n ①当n4时，因为存在m的6减数列， 所以数列中各项均不相同，所以m1234106． ②当n5时，因为存在m的6减数列， 所以数列各项中必有不同的项，所以m6． 若m6，满足要求的数列中有四项为1，一项为2， 学科网（北京）股份有限公司所以k 4，不符合题意，所以m6． ③当n6时，因为存在m的6减数列， 所以数列各项中必有不同的项，所以m6． 综上所述，若存在m的6减数列，则m6． （3）若数列中的每一项都相等，则k 0，若k 0，所以数列A存在大于1的项，若末项a 1， n 将a 拆分成a 个1后k变大，所以此时k不是最大值， n n 所以a 1．当i 1,2,,n1时，若a a ，交换a ,a 的顺序后k变为k1， n i i1 i i1 所以此时k不是最大值，所以a a ．若a a  0,1 ，所以a a 2， i i1 i i1 i i1 所以将a 改为a 1，并在数列末尾添加一项1，所以k变大， i i 所以此时k不是最大值，所以a a  0,1 ． i i1 若数列A中存在相邻的两项a 3,a 2，设此时A中有x项为2， i i1 将a 改为2，并在数列末尾添加一项1后，k的值至少变为kx1xk1， i 所以此时k不是最大值，所以数列A的各项只能为2或1，所以数列A为2,2,,2,1,1,,1的形式． 设其中有x项为2，有 y 项为1， 因为存在2024的k减数列，所以2x y 2024， 所以k  xy  20242x  x2x2 2024x2(x506)2 512072， 所以，当且仅当x506,y 1012时，k取最大值为512072． 学科网（北京）股份有限公司