文档内容
试卷第1页,共11页
1.由z 1 + i = 2 −i,z =
2−i
1+i =
2−i
1−i
1+i
1−i =
2−2i−i−1
2
=
1−3i
2
=
1
2 −
3
2 i,
所以z 的虚部为−
3
2.
故选:C.
2.
1
x < 1,解得x > 1 或x < 0,
故使得条件p 成立的一个充分不必要条件应为x > 1 或x < 0 的真子集,
其中x <−1 满足要求,其他选项不满足.
故选:A
3.y = tan( −3x +
π
6 ) =−tan 3x −
π
6 ,
令kπ −
1
2 π<3x−
π
6 < kπ +
1
2 π,k ∈Z,
解得
kπ
3 −
1
9 π 0,则−1 < f x < 3,
又x ≥0 时,f x =−
1
e
x
−1 单调递增,又−
1
e
x
< 0,则−2 ≤f x <−1,
作出f x 的图象如图,
由f x + 2 < f x2 ,x2 ≥0,
则0 ≤x + 2 < x2,解得−2 ≤x <−1 或x > 2,
所以实数x 的取值范围为[ −2, −1) ∪2, + ∞.
故选:C.
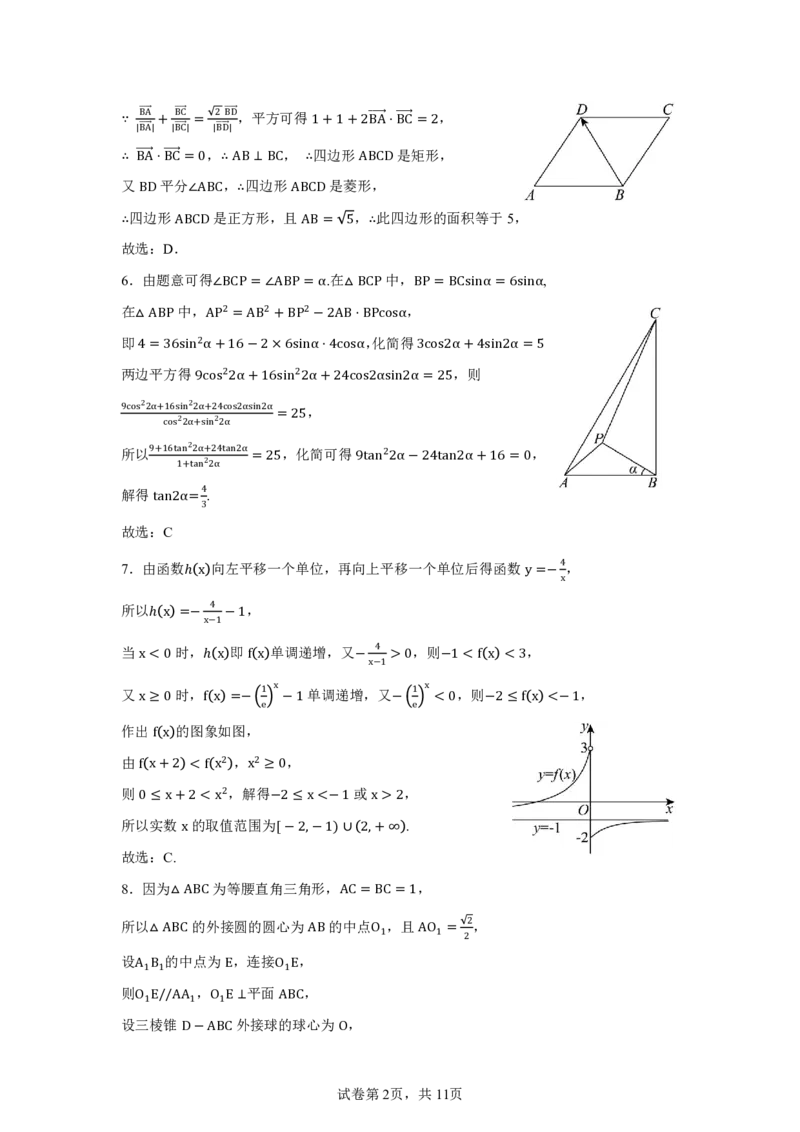
8.因为△ABC 为等腰直角三角形,AC = BC = 1,
所以△ABC 的外接圆的圆心为AB 的中点O1,且AO1 =
2
2 ,
设A1B1的中点为E,连接O1E,
则O1E//AA1,O1E ⊥平面ABC,
设三棱锥D −ABC 外接球的球心为O,
{#{QQABBYSUggggQBIAAQhCAQ2wCAAQkhAACQgGhAAMsAAByQFABAA=}#}
试卷第3页,共11页
由球的性质可得点O 在O1E 上,设OO1 = x,DE = t 0 ≤t ≤
2
2 ,
外接球的半径为R,因为OA = OD = R,
所以x2 +
2
2
2
=
(2 −x)2 + t2,即t2 = 4x −
7
2,
又0 ≤t ≤
2
2 ,则
7
8 ≤x ≤1,
因为R2 = x2 +
1
2,所以
81
64 ≤R2 ≤
3
2,则
9
8 ≤R ≤
6
2 ,
故选:B.
9.A 选项,a > 0,b > 0,ab ≤
a+b 2
4
=
9
4,当且仅当a = b =
3
2时,等号成立,A 正确;
B 选项,
a +
b
2 = a + b + 2 ab = 3 + 2 ab > 3,
故a +
b >
3,故B 错误.
C 选项,
b
a +
3+b
b =
b
a +
a+b+b
b
=
b
a +
a
b + 2 ≥2
b
a ⋅
a
b + 2 = 4,
当且仅当
b
a =
a
b,即a = b =
3
2时,等号成立,C 正确;
D 选项,
a2
a+1 +
b2
b+1 =
a+1 2−2 a+1 +1
a+1
+
b+1 2−2 b+1 +1
b+1
= a + 1 +
1
a+1 + b + 1 +
1
b+1 −4 =
1
a+1 +
1
b+1 + 1,
其中a > 0,b > 0,a + b = 3,故
a+1
5 +
b+1
5 = 1,
所以
1
a+1 +
1
b+1 =
1
a+1 +
1
b+1
a+1
5 +
b+1
5
=
2
5 +
a+1
5 b+1 +
b+1
5 a+1
≥
2
5 + 2
a+1
5 b+1 ⋅
b+1
5 a+1 =
4
5,
故
a2
a+1 +
b2
b+1 =
1
a+1 +
1
b+1 + 1 ≥
9
5,
当且仅当
a+1
5 b+1 =
b+1
5 a+1 ,即a = b =
3
2时,等号成立,D 正确.
故选:ACD
10.对于A,根据正弦定理可求得
a
sinA =
b
sinB,所以bsinA < a < b,
所以sinA <
a
b =
3
2 ,且A < B, 0 < A <
π
2,可求得0 < θ <
π
3,故A 错误;
对于B,直接根据aԦሬ在bԦሬ上的投影向量
aԦሬ·bԦሬ
|bԦሬ|2 ·bԦሬ=
10
( 5)2 ·(2,1) = (4,2),故B 正确;
对于C,aԦሬ−bԦሬ
=
(cosα −2)2 + (sinα −1)2 =
6 −4cosα −2sinα,
{#{QQABBYSUggggQBIAAQhCAQ2wCAAQkhAACQgGhAAMsAAByQFABAA=}#}
试卷第4页,共11页
则6 −4cosα −2sinα = 6 −2 5(
2
5 cosα +
1
5 sinα),令sinβ =
2
5 , cosβ =
1
5,
则aԦሬ−bԦሬ
=
5 −2 5sin(α + β) + 1,
当sin(α + β) =−1 时,aԦሬ−bԦሬ取最大值,最大值为5 + 1,故C 正确;
对于D,函数y = f x + 1 是偶函数,f x + 1 = f 1 −x ,f x = f 2 −x ,所以f x 的图象
关于直线x = 1 对称,函数y = f x + 2 是奇函数,所以f x 的图象关于2,0 对称,则f 2 −
x + f 2 + x = 0,可得f x + 4 =−f x + 2 = f x ,所以f x 是周期为4 的周期函数. 所以
f 2024 = f 4 × 506 = f 0 = 0,故D 正确.
故选:BCD.
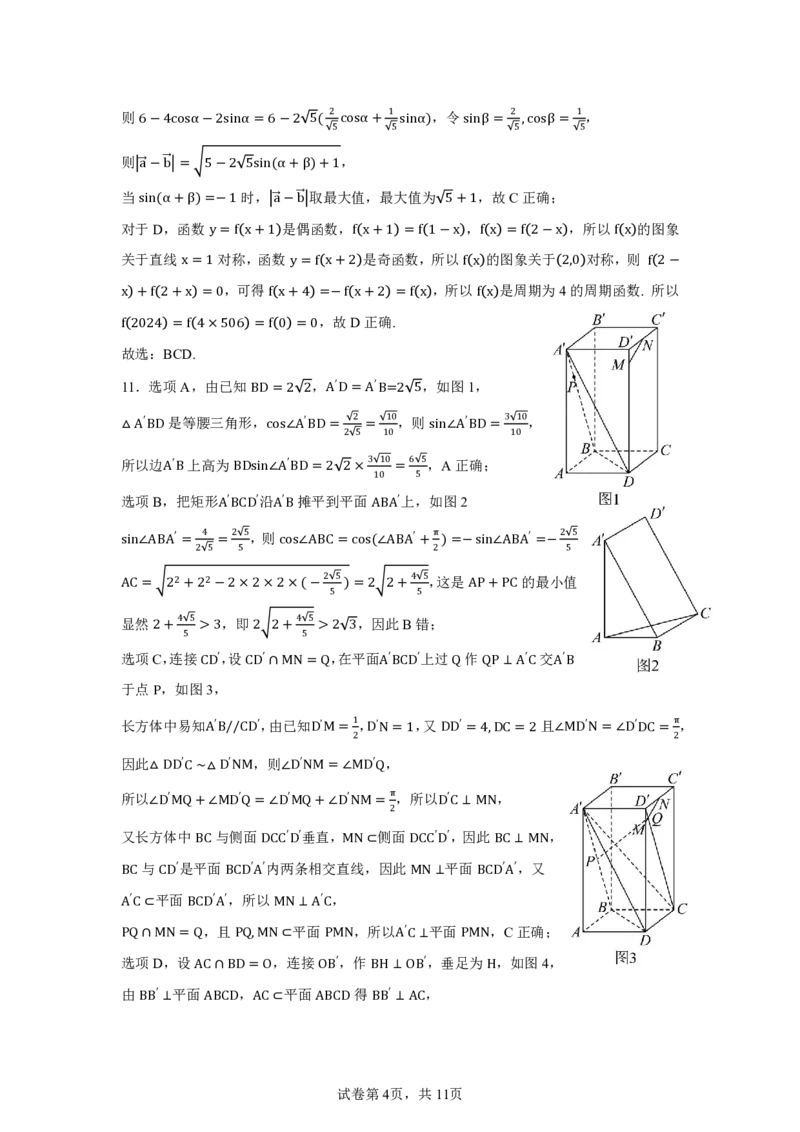
11.选项A,由已知BD = 2 2,A′D = A′ B=2 5,如图1,
△A′BD 是等腰三角形,cos∠A′BD =
2
2 5 =
10
10 ,则sin∠A′BD =
3 10
10 ,
所以边A′B 上高为BDsin∠A′BD = 2 2 ×
3 10
10 =
6 5
5 ,A 正确;
选项B,把矩形A′BCD′沿A′B 摊平到平面ABA′上,如图2
sin∠ABA′ =
4
2 5 =
2 5
5 ,则cos∠ABC = cos(∠ABA′ +
π
2 ) =−sin∠ABA′ =−
2 5
5
AC =
22 + 22 −2 × 2 × 2 × ( −
2 5
5 ) = 2 2 +
4 5
5 ,这是AP + PC 的最小值
显然2 +
4 5
5 > 3,即2 2 +
4 5
5 > 2 3,因此B 错;
选项C,连接CD′,设CD′ ∩MN = Q,在平面A′BCD′上过Q 作QP ⊥A′C 交A′B
于点P,如图3,
长方体中易知A′B//CD′,由已知D'M =
1
2,D'N = 1,又DD′ = 4, DC = 2 且∠MD′N = ∠D′DC =
π
2,
因此△DD′C ∼△D′NM,则∠D′NM = ∠MD′Q,
所以∠D′MQ + ∠MD′Q = ∠D′MQ + ∠D′NM =
π
2,所以D′C ⊥MN,
又长方体中BC 与侧面DCC′D′垂直,MN ⊂侧面DCC′D′,因此BC ⊥MN,
BC 与CD′是平面BCD′A′内两条相交直线,因此MN ⊥平面BCD′A′,又
A′C ⊂平面BCD′A′,所以MN ⊥A′C,
PQ ∩MN = Q,且PQ, MN ⊂平面PMN,所以A′C ⊥平面PMN,C 正确;
选项D,设AC ∩BD = O,连接OB′,作BH ⊥OB′,垂足为H,如图4,
由BB′ ⊥平面ABCD,AC ⊂平面ABCD 得BB′ ⊥AC,
{#{QQABBYSUggggQBIAAQhCAQ2wCAAQkhAACQgGhAAMsAAByQFABAA=}#}
试卷第5页,共11页
又正方形ABCD 中,AC ⊥BD,BD ∩BB′ = B,BD, BB′ ⊂平面BDD′B′,
所以AC ⊥平面BDD′B′,而BH ⊂平面BDD′B′,所以AC ⊥BH,
AC ∩B′O = O,AC, B′O ⊂平面AB′C,所以BH ⊥平面AB′C,
由已知BO =
2,BB′ = 4,则BH =
4 2
42+( 2)2 =
4
3,
平面AB'C 截球所得截面圆半径为r,则r =
(
17
6 )2 −(
4
3 )2 =
5
2,
所以截面圆面积为S = π × (
5
2 )2 =
25π
4 ,D 错.
故选:AC.
12.因为x0
2ex0 + lnx0 = 0 0 < x0 < 1 ,故x0ex0 =
1
x0 ln
1
x0 = ln
1
x0 e
ln 1
x0,
因为0 < x0 < 1,故
1
x0 > 1,所以ln
1
x0 > 0,设g x = xex, x > 0
则g′ x = x + 1 ex > 0,故g x 在0, + ∞上为增函数,
故x0 = ln
1
x0,故ex0 =
1
x0,且x0 =−lnx0,故ex0 −
3lnx0+1
x0
=−
3lnx0
x0 = 3,
故答案为:3.
13.根据向量加法三角形法则得到,AMԦ
ሬሬሬሬ= ABԦ
ሬሬሬ+ BMԦ
ሬሬሬሬ= ABԦ
ሬሬሬ+
1
2 (BCԦ
ሬሬሬ+ BB′Ԧ
ሬሬሬሬ),
即AMԦ
ሬሬሬሬ= ABԦ
ሬሬሬ+
1
2 ADԦ
ሬሬሬሬ+
1
2 AA′Ԧ
ሬሬሬሬ,即AM2 = (ABԦ
ሬሬሬ+
1
2 ADԦ
ሬሬሬሬ+
1
2 AA′Ԧ
ሬሬሬሬ)2,展开得到,
AMԦ
ሬሬሬሬ2 = ABԦ
ሬሬሬ2 +
1
4 ADԦ
ሬሬሬሬ2 +
1
4 AA′Ԧ
ሬሬሬሬ2
+ ABԦ
ሬሬሬ⋅ADԦ
ሬሬሬሬ+ ABԦ
ሬሬሬ⋅AA′Ԧ
ሬሬሬሬ+
1
2 ADԦ
ሬሬሬሬ⋅AA′Ԧ
ሬሬሬሬ,
运用数量积公式计算得到AMԦ
ሬሬሬሬ2 = 4 + 1 + 1 + 2 × 2 ×
1
2 + 2 × 2 ×
1
2 +
1
2 × 2 × 2 ×
1
2 = 11.
因为|AM
Ԧ
| =
AM
→
2,所以|AMԦ
ሬሬሬሬ| =
11.
故答案为:11.
14.∵f(x) = tanx,
∴f′(x) =
sinx
cosx
′
=
cosx⋅cosx−sinx⋅(−sinx)
cos2x
=
cos2x+sin2x
cos2x
= 1 + tan2x,
∵f(an+1) =
f′(an),
∴tanan+1 =
1 + tan2an,
∴tan2an+1 = 1 + tan2an,即tan2an+1 −tan2an = 1,
∵tana1 = tan
π
4 = 1,
∴tan2an 是以1 为首项,1 为公差的等差数列,
{#{QQABBYSUggggQBIAAQhCAQ2wCAAQkhAACQgGhAAMsAAByQFABAA=}#}
试卷第6页,共11页
∴tan2an = n,
∵an ∈0,
π
2 ,
∴tanan > 0,
∴tanan =
n,
∴bn =
(−1)n
tanan+1−tanan =
(−1)n
(n+1)−n = ( −1)n( (n + 1) +
n),
∴T440 = b1 + b2 + b3 + ⋯+ b439 + b440
=−( 2 + 1) + ( 3 +
2) −( 4 +
3) + ⋯−( 440 +
439) + ( 441 +
440)
=
441 −1 = 21 −1 = 20.
故答案为:20.
15.(1)f x = sin x +
π
3 ⋅sin x +
2π
3
−
1
2
=
1
2 sinx +
3
2 cosx
−1
2 sinx +
3
2 cosx
−1
2
= 3
4 cos2x −1
4 sin2x −1
2
=
1
4 −sin2x,
则f A =
1
4 −sin2A = 0,
因为A ∈0, π ,所以sinA > 0,所以sinA =
1
2,
所以A =
π
6或A =
5π
6 ;…………………………………………………………………………6 分
(2)若角A 为锐角,则A =
π
6,
设角A, B, C 的对边分别为a, b, c,
则S =
1
2 bcsinA =
3
4 b =
9 3
4 ,所以b = 3 3,………………………………………………8 分
如图,连接CF,
因为点E、F 为边AB 上的三等分点,所以E 为AF 的中点,
因为点D 为边AC 的中点,所以点M 为△ACF 的重心,
则CMԦ
ሬሬሬሬ=
2
3 CEԦ
ሬሬሬ=
2
3 AEԦ
ሬሬሬ−ACԦ
ሬሬሬ
=
2
3
1
2 AFԦ
ሬሬሬ−ACԦ
ሬሬሬ
=
1
3 AFԦ
ሬሬሬ−
2
3 ACԦ
ሬሬሬ,
所以AMԦ
ሬሬሬሬ= ACԦ
ሬሬሬ+ CMԦ
ሬሬሬሬ=
1
3 AFԦ
ሬሬሬ+ ACԦ
ሬሬሬ,
又AFԦ
ሬሬሬ
= 2, ACԦ
ሬሬሬ
= 3 3,
{#{QQABBYSUggggQBIAAQhCAQ2wCAAQkhAACQgGhAAMsAAByQFABAA=}#}
试卷第7页,共11页
所以AMԦ
ሬሬሬሬ
=
1
9 AFԦ
ሬሬሬ+ ACԦ
ሬሬሬ
2 =
1
3
AFԦ
ሬሬሬ2 + ACԦ
ሬሬሬ2 + 2AFԦ
ሬሬሬ⋅ACԦ
ሬሬሬ=
1
3
4 + 27 + 18 =
7
3,
即线段AM 的长为
7
3.………………………………………………………………………13 分
16.(1)因为cosA+cosB
cosA−cosB = sinC sinC−2sinA ,
所以cos2A −cos2B = sin2C −
2sinCsinA,
即sin2C + sin2A −sin2B =
2sinCsinA.
由正弦定理得c2 + a2 −b2 =
2ca,
由余弦定理得cosB=
2
2 ,
由B ∈0, π ,知B =
π
4.
………………………………………………………………………6
分
(2)由cosA=
10
10 ,可得A ∈0,
π
2 ,
进而可得sinA=
3 10
10 ,
由B =
π
4,可得sinB=
2
2 ,
则sinC=sin A + B = sinAcosB + sinBcosA =
3 10
10 ×
2
2 +
10
10 ×
2
2 =
2 5
5 ,……………10 分
由正弦定理可知
b
c =
sinB
sinC =
10
4 ,
又因为b + c =
5 + 2 2,解得b =
5, c = 2 2,
所以△ABC 的面积为
S =
1
2 bcsinA =
1
2 ×
5 × 2 2 ×
3 10
10 = 3.…………………………………………………15 分
17.(1)选择①②,可证明③.
由PA = PB,D 是线段AB 的中点,得PD⊥AB.
又平面PAB⊥平面ABC,平面PAB ∩平面ABC = AB,且PD ⊂平面PAB;
所以PD⊥平面ABC,
AC⊂平面ABC,得PD⊥AC,
又DE⊥AC;PD ∩DE = D,PD, DE ⊂平面PDE,
所以AC⊥平面PDE.
{#{QQABBYSUggggQBIAAQhCAQ2wCAAQkhAACQgGhAAMsAAByQFABAA=}#}
试卷第8页,共11页
因为PE ⊂平面PDE,所以
AC ⊥PE,
…………………………………………………………………………6 分
若选择①③,可证明②.
由PA = PB,D 是线段AB 的中点,得PD⊥AB.
又平面PAB⊥平面ABC,平面PAB ∩平面ABC = AB,且PD ⊂平面PAB;
所以PD⊥平面ABC,
AC ⊂平面ABC,得PD ⊥AC,
又PE⊥AC,PD ∩PE = P,PD, PE ⊂平面PDE,所以AC⊥平面PDE,
因为DE ⊂平面PDE,所以AC ⊥DE.………………………………………………………6 分
选择②③,可证明①.
由PA = PB,D 是线段AB 的中点,得PD⊥AB
因为PE⊥AC,DE⊥AC,PD, PE ⊂平面PDE,DE ∩PE = E,
所以AC⊥平面PDE.
PD⊂平面PDE,得PD⊥AC,
AB ∩AC = A,AB, AC ⊂平面ABC,所以PD⊥平面ABC.
又PD ⊂平面PAB,故平面PAB⊥平面ABC.
…………………………………………6 分
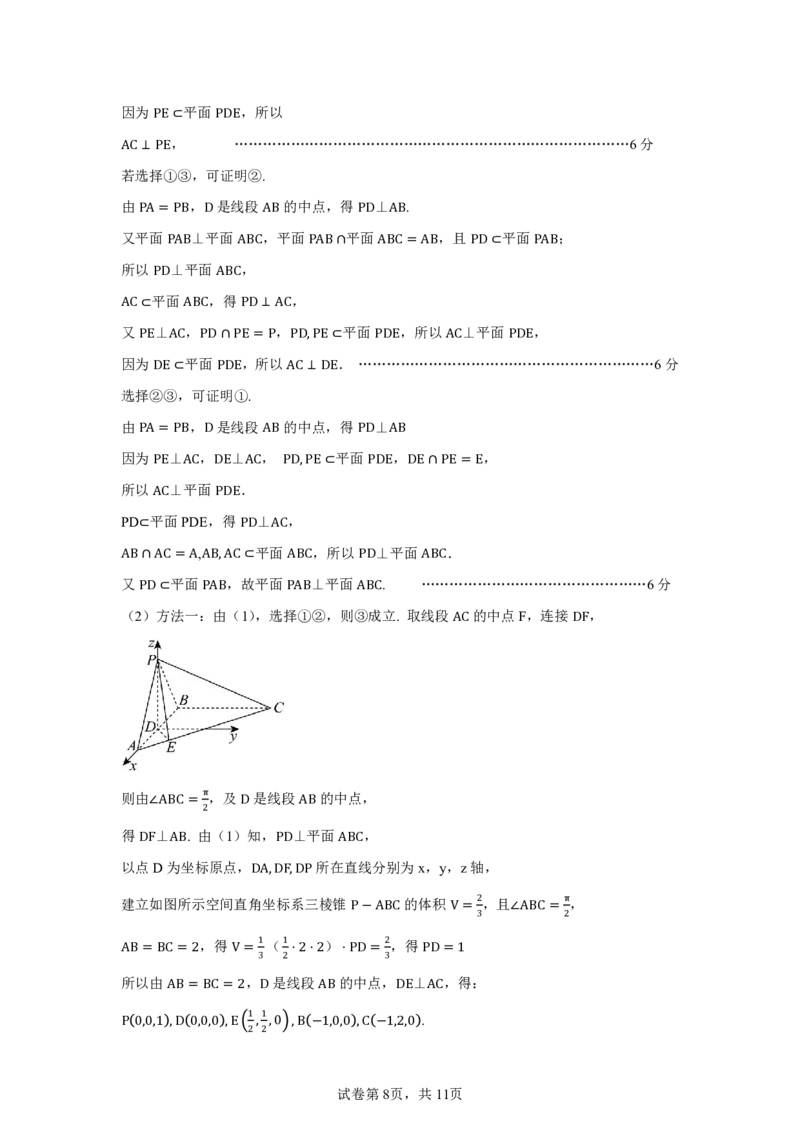
(2)方法一:由(1),选择①②,则③成立. 取线段AC 的中点F,连接DF,
则由∠ABC =
π
2,及D 是线段AB 的中点,
得DF⊥AB. 由(1)知,PD⊥平面ABC,
以点D 为坐标原点,DA, DF,DP 所在直线分别为x,y,z 轴,
建立如图所示空间直角坐标系三棱锥P −ABC 的体积V =
2
3,且∠ABC =
π
2,
AB = BC = 2,得V =
1
3 (
1
2 ⋅2 ⋅2)⋅PD =
2
3,得PD = 1
所以由AB = BC = 2,D 是线段AB 的中点,DE⊥AC,得:
P 0,0,1 , D 0,0,0 , E
1
2 ,
1
2 , 0 , B −1,0,0 , C −1,2,0 .
{#{QQABBYSUggggQBIAAQhCAQ2wCAAQkhAACQgGhAAMsAAByQFABAA=}#}
试卷第9页,共11页
所以DPԦ
ሬሬሬ= 0,0,1 ,DEԦ
ሬሬሬ=
1
2 ,
1
2 , 0 ,BPԦ
ሬሬሬ= 1,0,1 ,BCԦ
ሬሬሬ= 0,2,0 .
设面PDE 与面PBC 的法向量分别为n1Ԧ
ሬሬሬ= (x1, y1, z1),n2Ԧ
ሬሬሬ= (x2, y2, z2),
则
z1 = 0
1
2 x1 +
1
2 y1 = 0 ,得:
z1 = 0
x1 =−y1 ,所以面PDE 的一个法向量为n1Ԧ
ሬሬሬ= (1, −1,0).
x2 + z2 = 0
2y2 = 0
,得:x2 =−z2
y2 = 0 ,所以面PBC 的一个法向量为n2Ԧ
ሬሬሬ= (1,0, −1).
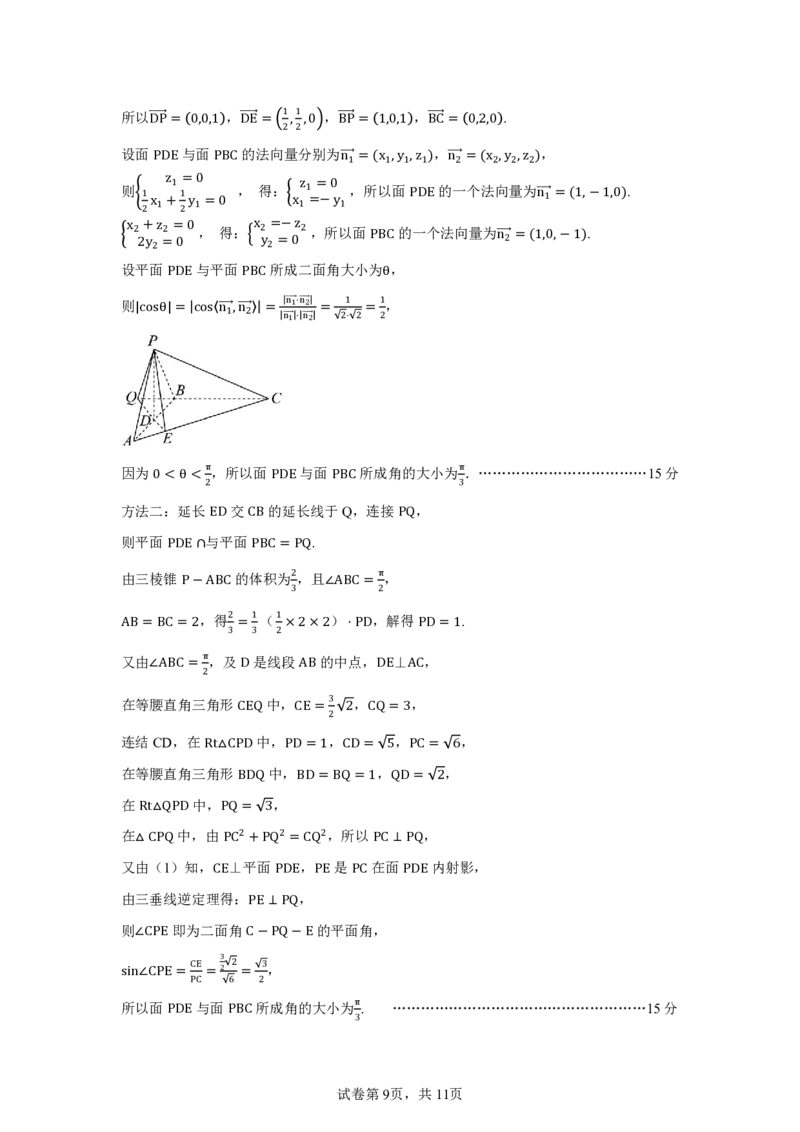
设平面PDE 与平面PBC 所成二面角大小为θ,
则|cosθ| = cos n1Ԧ
ሬሬሬ, n2Ԧ
ሬሬሬ
=
n1Ԧ
ሬሬሬ⋅n2Ԧ
ሬሬሬ
n1Ԧ
ሬሬሬ⋅n2Ԧ
ሬሬሬ=
1
2⋅2 =
1
2,
因为0 < θ <
π
2,所以面PDE 与面PBC 所成角的大小为
π
3.………………………………15 分
方法二:延长ED 交CB 的延长线于Q,连接PQ,
则平面PDE ∩与平面PBC = PQ.
由三棱锥P −ABC 的体积为
2
3,且∠ABC =
π
2,
AB = BC = 2,得
2
3 =
1
3 (
1
2 × 2 × 2)⋅PD,解得PD = 1.
又由∠ABC =
π
2,及D 是线段AB 的中点,DE⊥AC,
在等腰直角三角形CEQ 中,CE =
3
2
2,CQ = 3,
连结CD,在Rt△CPD 中,PD = 1,CD =
5,PC =
6,
在等腰直角三角形BDQ 中,BD = BQ = 1,QD =
2,
在Rt△QPD 中,PQ =
3,
在△CPQ 中,由PC2 + PQ2 = CQ2,所以PC ⊥PQ,
又由(1)知,CE⊥平面PDE,PE 是PC 在面PDE 内射影,
由三垂线逆定理得:PE ⊥PQ,
则∠CPE 即为二面角C −PQ −E 的平面角,
sin∠CPE =
CE
PC =
3
2 2
6 =
3
2 ,
所以面PDE 与面PBC 所成角的大小为
π
3.
………………………………………………15 分
{#{QQABBYSUggggQBIAAQhCAQ2wCAAQkhAACQgGhAAMsAAByQFABAA=}#}
试卷第10页,共11页
18.(1)如图:b3 = 7,b4 = 11,
………………………………………………………4 分
(2)记线段上n 个点最多将其划分成an段,则an = n + 1,
为使划分区域块尽可能多,
新添加的一条直线ln,与前n −1 条直线l1,l2,⋯,ln−1都相交,有n −1 个不同的交点,
这些点把直线ln分成n 段,每一段又把原区域一分为二,则新增an−1 = n 个区域块,
即bn −bn−1 = an−1 = n,
)
2
(
n
,且b1 = 2,,
故bn = b1 +
i=1
n−1 ai
σ
= 2 + 2 + 3 + ⋯+ n =
n2+n+2
2
.………………………………………10 分
(3)记第k 刀所形成的切面所在平面为αk,
若切第n 刀,新增切面平面αn与前n −1 个平面α1,α2,α3,⋯,αn−1都相交,有n −1 条
不同的直线l1,l2,l3,⋯,ln−1,
这些直线把平面αn划分的区块数即为新增的空间区块数,
由(2)可知为使此数最大,则cn −cn−1 = bn−1,
)
2
(
n
,且c1 = 2,
故cn = c1 +
i=1
n−1 bi
σ
=
i=1
n−1 i2+i+2
2
=
1 +
1
2
i=1
n−1 i2
+
1
2
i=1
n−1 i
σ
+
i=1
n−1 1
σ
= 2 +
1
12 (n −1)n(2n −1) +
n(n−1)
4
+ n −1 =
1
6 n3 +
5
6 n + 1,
则c4 =
1
6 × 43 +
5
6 × 4 + 1 = 15,故此时最少切4 下即可.…………………………………17 分
19.(1)由题可得f′ x =−2cosxsinx ⋅cos2x + cos2x ⋅−2sin2x =−2sinxcosx ⋅4cos2x −1
=−2sinxcosx 2cosx −1
2cosx + 1 .
令f′ x = 0 在x ∈(0, π)上的根为x1 =
π
3 , x2 =
π
2 , x3 =
2π
3 ,
当x ∈0,
π
3 时,f′ x < 0, f x 单调递减;当x ∈
π
3 ,
π
2 时,f′ x > 0, f x 单调递增;
当x ∈
π
2 ,
2π
3 时,f′ x < 0, f x 单调递减;当x ∈
2π
3 , π 时,f′ x > 0, f x 单调递增.
综上,f x 在0,
π
3 和
π
2 ,
2π
3 上单调递减,在
π
3 ,
π
2 和
2π
3 , π 上单调递增.
………………………………………………………………6 分
{#{QQABBYSUggggQBIAAQhCAQ2wCAAQkhAACQgGhAAMsAAByQFABAA=}#}
试卷第11页,共11页
(2)因为f x + π = cos2 x + π cos2 x + π = cos2xcos2x = f x ,
所以f x 的一个正周期为π.
故函数f(x)在0, π 的最大与最小值即f x 的最大值和最小值.
根据(1)中结论,又f 0 = 1, f
π
3
=−
1
8 , f
π
2
= 0, f
2π
3
=−
1
8 , f π = 1,
所以f x 在0, π 的最大值为1,最小值为−
1
8.
故f x 的最大值为1,最小值为−
1
8.
………………………………………………12 分
(3)证明:cosxsin33xf x f 2x f 4x ⋯f 2nx = sin33xcos3xcos32xcos34x⋯cos32nx ⋅cos2n+1x
≤sin33xcos3xcos32xcos34x⋯cos32nx ,
又sin3x=sinxcos2x+cosxsin2x=sinx 1 −2sin2x + 2sinx 1 −sin2x = 3sinx −4sin3x,
所以sin3x cosxcos2xcos4xcos8x⋯cos2nx
= 3 −4sin2x sinx cosxcos2xcos22x⋯cos2nx
≤3 sinx cosxcos2xcos4x⋯cos2nx ≤3 ⋅
sin2n+1x
2n+1
≤
3
2n+1,
所以cosxsin33xf x f 2x f 4x ⋯f 2nx ≤
27
23n+3,得证.
…………………………………………………………………………………17 分
{#{QQABBYSUggggQBIAAQhCAQ2wCAAQkhAACQgGhAAMsAAByQFABAA=}#}