文档内容
北京市朝阳区 2024~2025 学年度第一学期期中质量检测
高三数学试卷
2024.11
(考试时间120分钟 满分150分)
本试卷分为选择题40分和非选择题110分
第一部分(选择题 共40分)
一、选择题共10小题,每小题4分,共40分.在每小题列出的四个选项中,选出符合题目要
求的一项.
1. 设集合 ,集合 ,则 ( )
A. B.
C. D.
2. 若函数 在 处取得最小值,则 ( )
A. 1 B. C. 2 D. 4
的
3. 下列函数中,既是奇函数又在区间 上单调递增 是( )
.
A B.
C. D.
4. 如图,在 中, , ,则( )A. B.
C. D.
5. 已知单位向量 , 满足 ,设向量 ,则向量 与向量 夹角的余弦值是( )
A. B. C. D.
6. 《九章算术》是我国古代数学名著,书中有如下的问题:“今有女子善织,日自倍,五日织五尺,问日
织几何?”意思是:“一女子善于织布,每天织的布都是前一天的2倍,已知她5天共织布5尺,问这女子
每天分别织布多少?”.由此推算,在这5天中,织布超过1尺的天数共有( )
.
A 1天 B. 2天 C. 3天 D. 4天
7. 已知 均为第二象限角,则“ ”是“ ”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
8. 已知函数 若直线 与函数 的图象有且只有一个公共点,则实
数 的取值范围是( )
A. B.
C. D.
9. 在三棱锥 中,棱 , , 两两垂直,点 在底面 内,已知点 到 , ,所在直线的距离分别为1,2,2,则线段 的长为( )
A. B. C. 3 D.
10. 数学家康托尔创立了集合论,集合论的产生丰富了现代计数方法.记 为集合 的元素个数, 为
集合 的子集个数,若集合 满足:① , ;②
,则 的最大值是( )
A. 99 B. C. D. 96
第二部分(非选择题 共110分)
二、填空题共5小题,每小题5分,共25分.
11. 复数 __________.
12. 在 中,已知 ,则 __________; ________.
13. 已知数列 的前n项和为 (A,B为常数),写出一个有序数对 ________,
使得数列 是递增数列.
14. 某种灭活疫苗的有效保存时间 (单位: )与储藏的温度 (单位:℃)满足函数关系 (
为常数,其中 ).已知该疫苗在0℃时的有效保存时间是1440h,在5℃时的有效保存时
间是360h,则该疫苗在10℃时的有效保存时间是________h.
15. 对于无穷数列 ,若存在常数 ,使得对任意的 ,都有不等式
成立,则称数列 具有性质 . 给出下列四个结论:①存在公差不为 的等差数列 具有性质 ;
②以 为首项, 为公比的等比数列 具有性质 ;
③若由数列 的前 项和构成的数列 具有性质 ,则数列 也具有性质 ;
④若数列 和 均具有性质 ,则数列 也具有性质 .
其中所有正确结论的序号是________.
三、解答题共6小题,共85分.解答应写出文字说明,演算步骤或证明过程.
16. 在 中, .
(1)求 的值;
(2)若 , ,求b及 的面积.
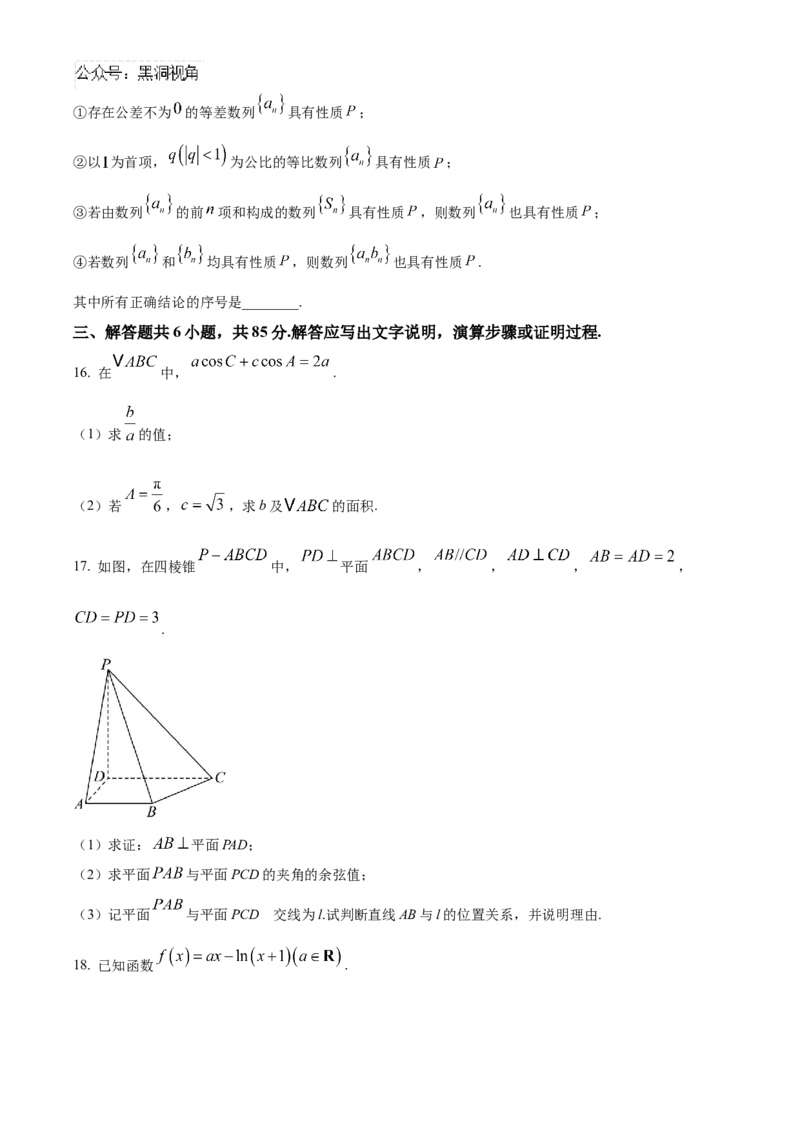
17. 如图,在四棱锥 中, 平面 , , , ,
.
(1)求证: 平面PAD;
(2)求平面 与平面PCD的夹角的余弦值;
的
(3)记平面 与平面PCD 交线为l.试判断直线AB与l的位置关系,并说明理由.
18. 已知函数 .(1)若 ,求 的最小值;
(2)若 存在极小值,求 的取值范围.
19. 设函数 .
(1)若 , ,求 的值;
(2)已知 在区间 上单调递增,且 是函数 的图象的对称轴,再从条件①、条
件②、条件③这三个条件中选择一个作为已知,使函数 存在,求ω,φ的值.
条件①:当 时, 取到最小值;
条件②: ;
条件③: 在区间 上单调递减.
注:如果选择的条件不符合要求,第(2)问得0分;如果选择多个符合要求的条件分别解答,按第一个解
答计分.
.
20 已知函数 .
(1)求曲线 在点 处的切线方程;
(2)讨论 在区间 上的零点个数;
(3)若 ,其中 ,求证: .
21. 若有穷正整数数列A: , , ,…, 满足如下两个性质,则称数列A为T数列:①;②对任意的 ,都存在正整数 ,使得
.
(1)判断数列A:1,1,1,3,3,5和数列B:1,1,2,2,4,4,4,12是否为T数列,说明理由;
(2)已知数列A: , , ,…, 是T数列.
(i)证明:对任意的 , 与 不能同时成立;
(ii)若n为奇数,求 的最大值.