文档内容
山东省实验中学 2023 级十月测试
数学试题
说明:试题分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第Ⅰ卷为第1页至第2页,
第Ⅱ卷为第2页至第4页.考试时间120分钟.
第Ⅰ卷(选择题 58分)
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是
符合题目要求的.
1. 已知点 关于z轴的对称点为B,则 等于( )
A. B. C. 2 D.
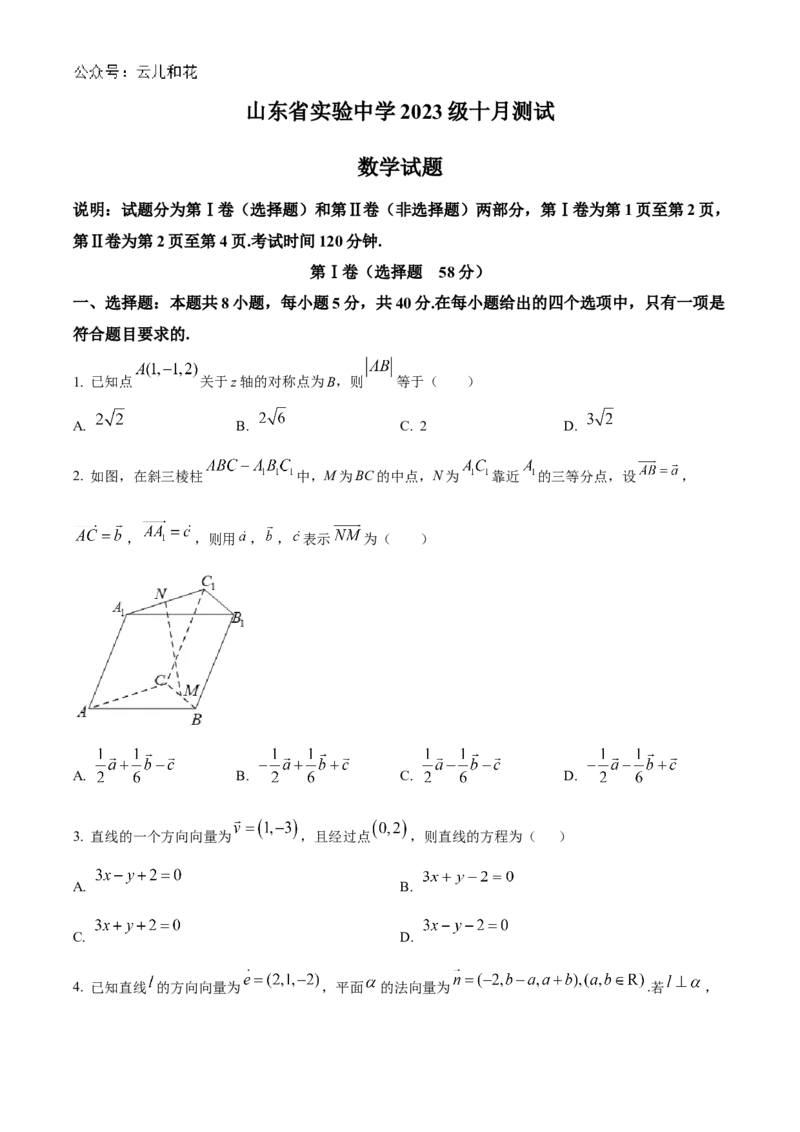
2. 如图,在斜三棱柱 中,M为BC的中点,N为 靠近 的三等分点,设 ,
, ,则用 , , 表示 为( )
A. B. C. D.
3. 直线的一个方向向量为 ,且经过点 ,则直线的方程为( )
A. B.
C. D.
4. 已知直线 的方向向量为 ,平面 的法向量为 .若 ,则 的值为( )
A. B. C. D.
5. “ ”是“直线 与 平行”的( )
A. 充分不必要条件 B. 必要不充分条件
.
C 充要条件 D. 既不充分也不必要条件
6. 正四面体 的棱长为2,点D是 的中点,则 的值为( )
A. B. C. D.
7. 已知正方形的一条对角线所在直线的斜率为 ,则其一条边所在直线的斜率是( )
A. B. C. D.
8. 设动点 在棱长为 的正方体 的对角线 上, ,当 为锐角时,
的取值范围是( )
A. B. C. D.
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的四个选项中,有多项符合
题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9. 已知向量 , , ,则下列结论正确的是( )A. 与 垂直 B. 与 共线
C. 与 所成角为锐角 D. , , ,可作为空间向量的一组基底
10. 已知两直线 , ,则下列说法正确的是( )
A. 对任意实数m,直线 , 的方向向量都不可能平行
在
B. 存 实数m,使直线 垂直于x轴
C. 存在实数m,使直线 , 互相垂直
D. 当 时,直线 的方向向量不存在
11. 在正三棱柱 中, ,点 满足⃑BP=λ⃑BC+μ⃑BB ,其中 ,
1
,则( )
A. 当 时, 的周长为定值
B. 当 时,三棱锥 的体积为定值
C. 当 时,有且仅有一个点 ,使得
D. 当 时,有且仅有一个点 ,使得 平面
第Ⅱ卷(非选择题 共92分)
三、填空题:本题共3小题,每小题5分,共15分.
12. 已知向量 , ,若 与 垂直,则 =_____.
13. 已知点 , ,直线 是过点 且与线段AB相交且斜率存在,则 的斜率 的取
值范围是____________14. 在 中,已知 , 边上的高线所在的直线方程为 , 边上的高线所在的直
线方程为 .则 边所在的直线方程为_______.
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15. 已知空间中三点 ,设 .
(1)若 ,且 ,求向量 ;
(2)求以 为一组邻边的平行四边形的面积 .
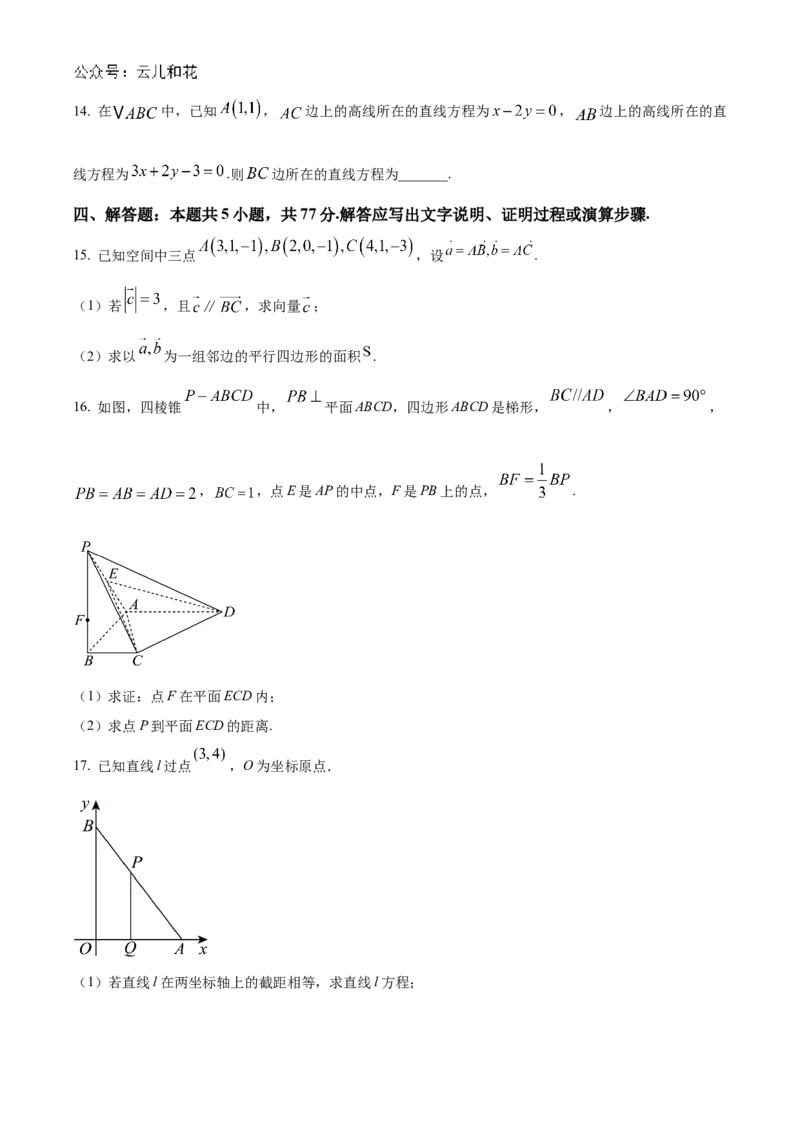
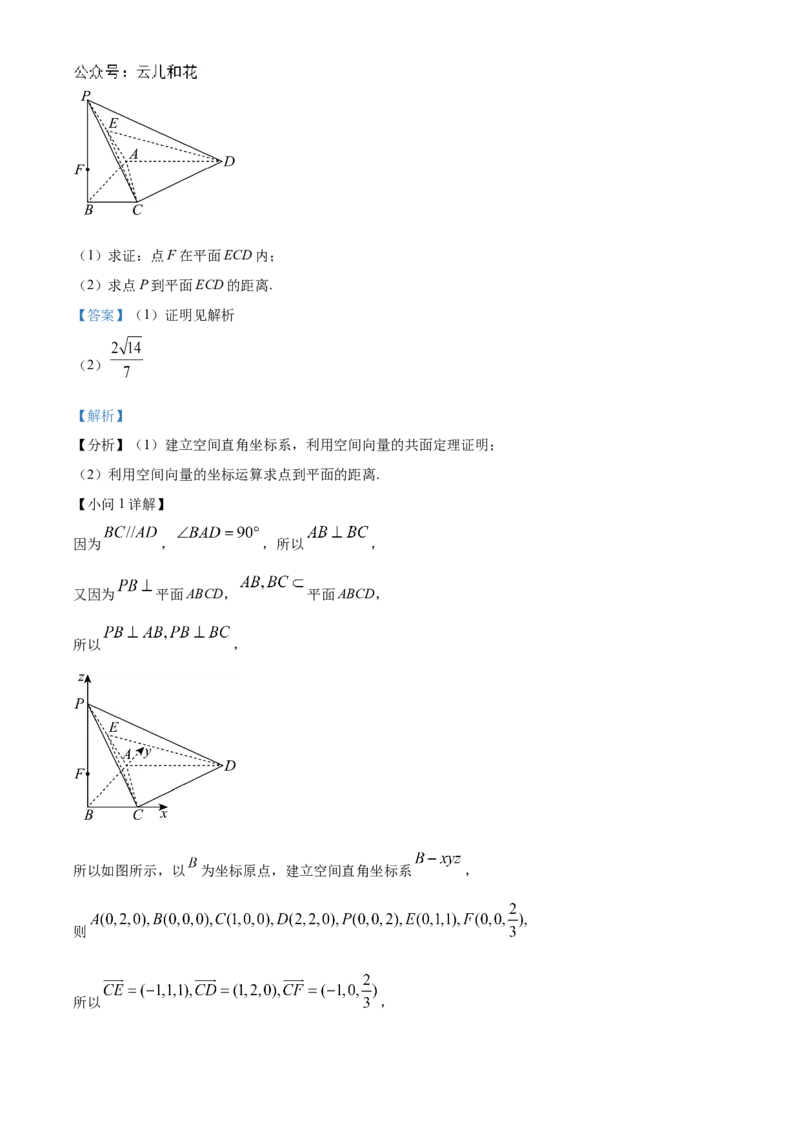
16. 如图,四棱锥 中, 平面ABCD,四边形ABCD是梯形, , ,
, ,点E是AP的中点,F是PB上的点, .
(1)求证:点F在平面ECD内;
(2)求点P到平面ECD的距离.
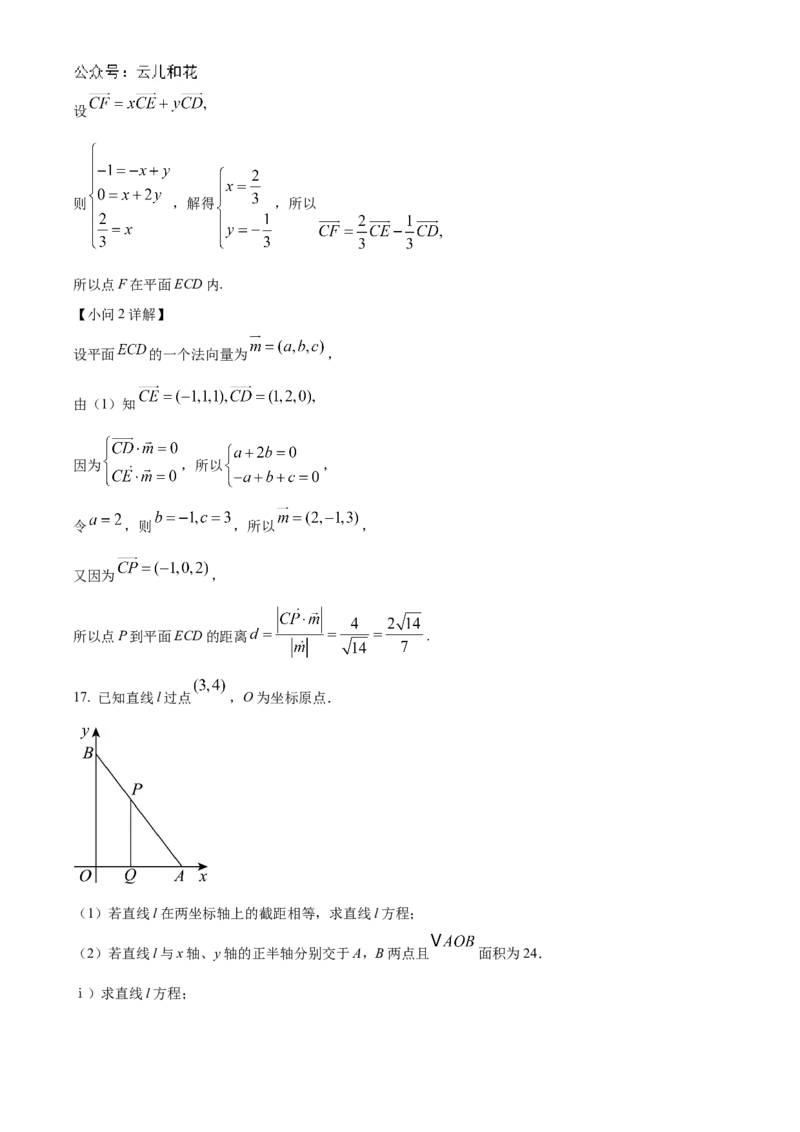
17. 已知直线l过点 ,O为坐标原点.
(1)若直线l在两坐标轴上的截距相等,求直线l方程;(2)若直线l与x轴、y轴的正半轴分别交于A,B两点且 面积为24.
ⅰ)求直线l方程;
ⅱ)若点P为线段AB上一动点,且 交OA于点Q.在y轴上是否存在点M,使 为等腰
直角三角形,若存在,求出点M的坐标;若不存在,说明理由.
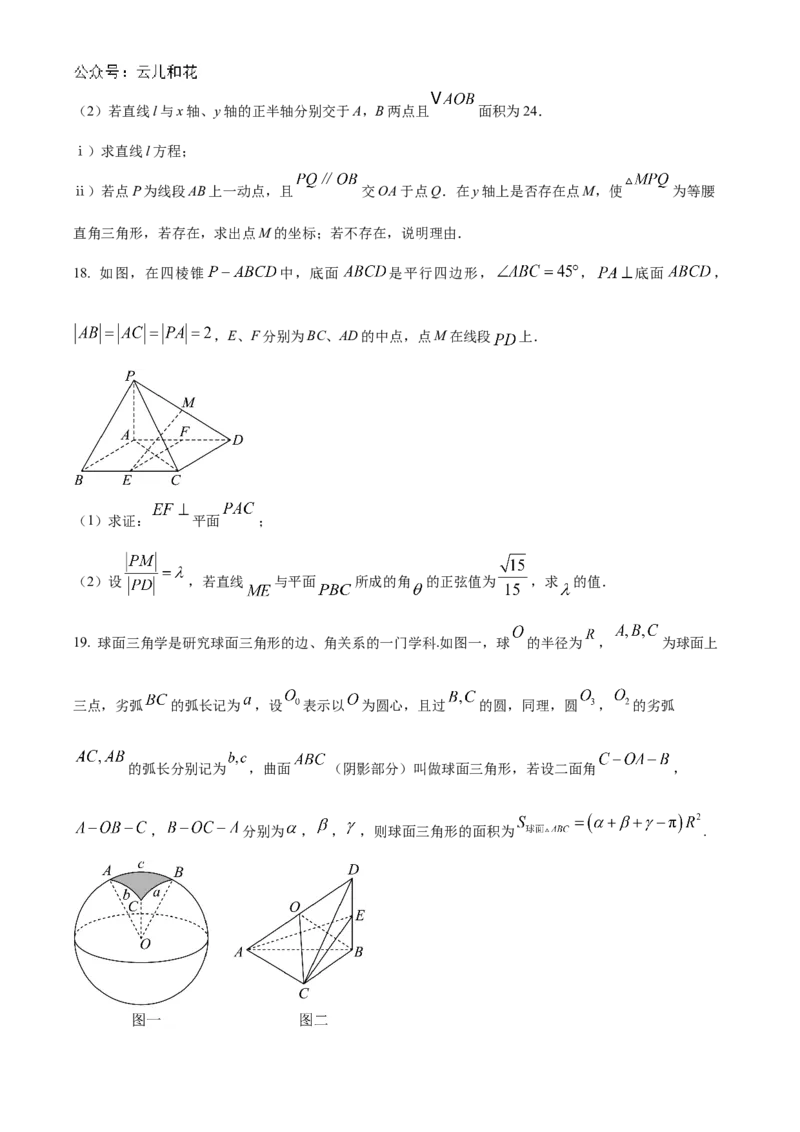
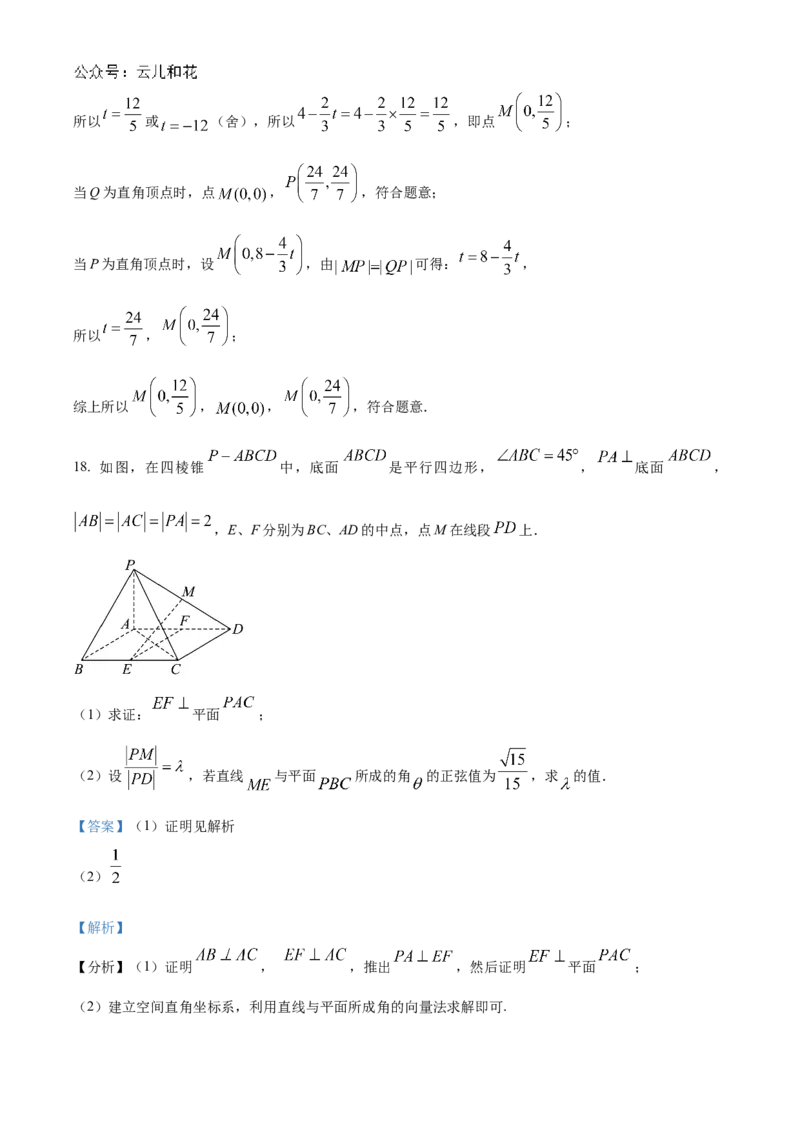
18. 如图,在四棱锥 中,底面 是平行四边形, , 底面 ,
,E、F分别为BC、AD的中点,点M在线段 上.
(1)求证: 平面 ;
(2)设 ,若直线 与平面 所成的角 的正弦值为 ,求 的值.
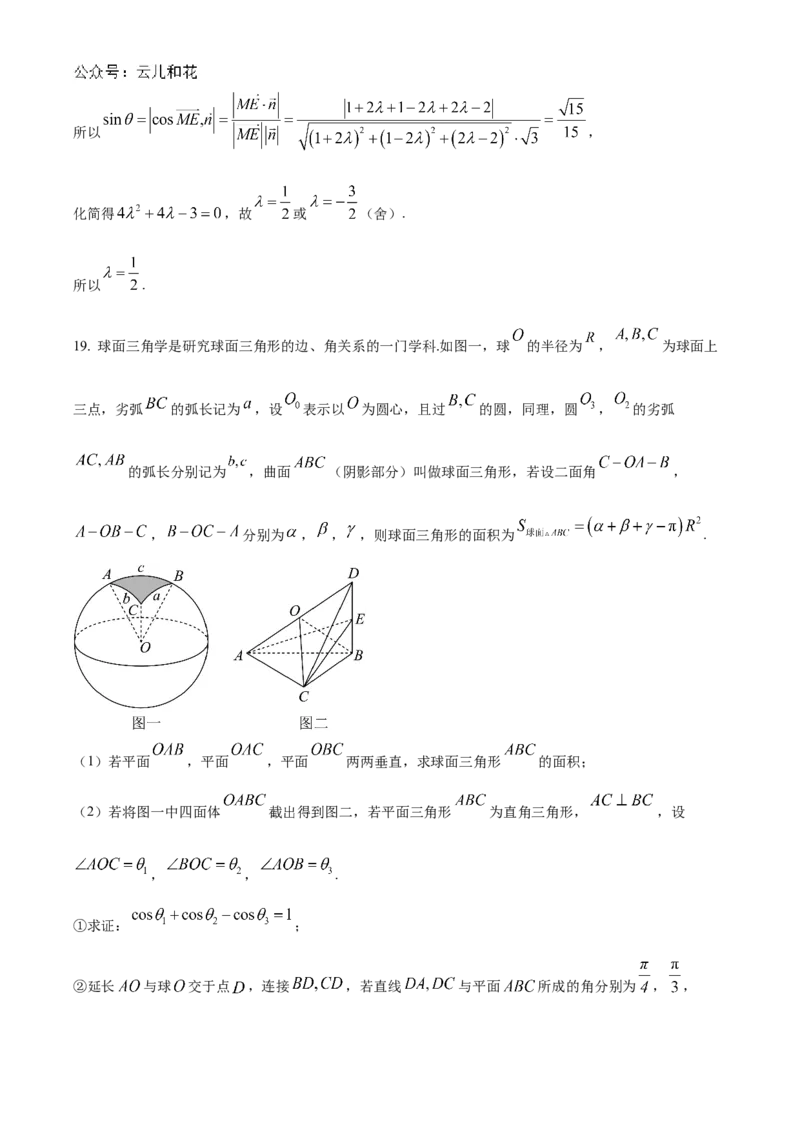
19. 球面三角学是研究球面三角形的边、角关系的一门学科.如图一,球 的半径为 , 为球面上
三点,劣弧 的弧长记为 ,设 表示以 为圆心,且过 的圆,同理,圆 , 的劣弧
的弧长分别记为 ,曲面 (阴影部分)叫做球面三角形,若设二面角 ,
, 分别为 , , ,则球面三角形的面积为 .的
(1)若平面 ,平面 ,平面 两两垂直,求球面三角形 面积;
(2)若将图一中四面体 截出得到图二,若平面三角形 为直角三角形, ,设
, , .
①求证: ;
②延长 与球 交于点 ,连接 ,若直线 与平面 所成 角的分别为 , ,
, , 为 中点, 为 中点,设平面 与平面 的夹角为 ,求
的最小值.山东省实验中学 2023 级十月测试
数学试题
说明:试题分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第Ⅰ卷为第1页至第2页,
第Ⅱ卷为第2页至第4页.考试时间120分钟.
第Ⅰ卷(选择题 58分)
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是
符合题目要求的.
1. 已知点 关于z轴的对称点为B,则 等于( )
A. B. C. 2 D.
【答案】A
【解析】
【分析】由点关于某坐标轴对称的点的特征以及两点距离公式即可求解.
【详解】点 关于z轴的对称点为B ,
所以 .
故选:A.
的
2. 如图,在斜三棱柱 中,M为BC 中点,N为 靠近 的三等分点,设 ,
, ,则用 , , 表示 为( )
A. B. C. D.【答案】A
【解析】
【分析】结合图形,根据空间向量的线性运算即可得到答案.
【详解】
故选:A
3. 直线的一个方向向量为 ,且经过点 ,则直线的方程为( )
A. B.
C. D.
【答案】B
【解析】
【分析】方法一:由直线的方向量求出直线斜率,然后利用点斜式可求出直线方程;方法二:由已知可得
直线的一个法向量为 ,则设直线为 ,再将 代入求出 ,从而可得直线方程.
【详解】方法一 ∵直线的一个方向向量为 ,∴ ,
∴直线的方程为 ,即 .
方法二 由题意知直线的一个法向量为 ,
∴直线的方程可设为 ,将点 代入得 ,
故所求直线的方程为 .
故选:B
4. 已知直线 的方向向量为 ,平面 的法向量为 .若 ,
则 的值为( )
A. B. C. D.【答案】B
【解析】
【分析】依题意可得 ,则 ,即可得到方程组,解得 、 的值,即可得解.
【详解】因为直线 的方向向量为 ,平面 的法向量为 且
,
所以 ,则 ,即 ,
所以 ,解得 ,所以 .
故选:B
的
5. “ ”是“直线 与 平行” ( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
【答案】C
【解析】
【分析】根据直线平行的条件,判断“ ”和“直线 与 平
行”之间的逻辑关系,即可得答案.
【详解】当 时,直线 与 平行;
当直线 与 平行时,
有 且 ,解得 ,
故“ ”是“直线 与 平行”的充要条件,
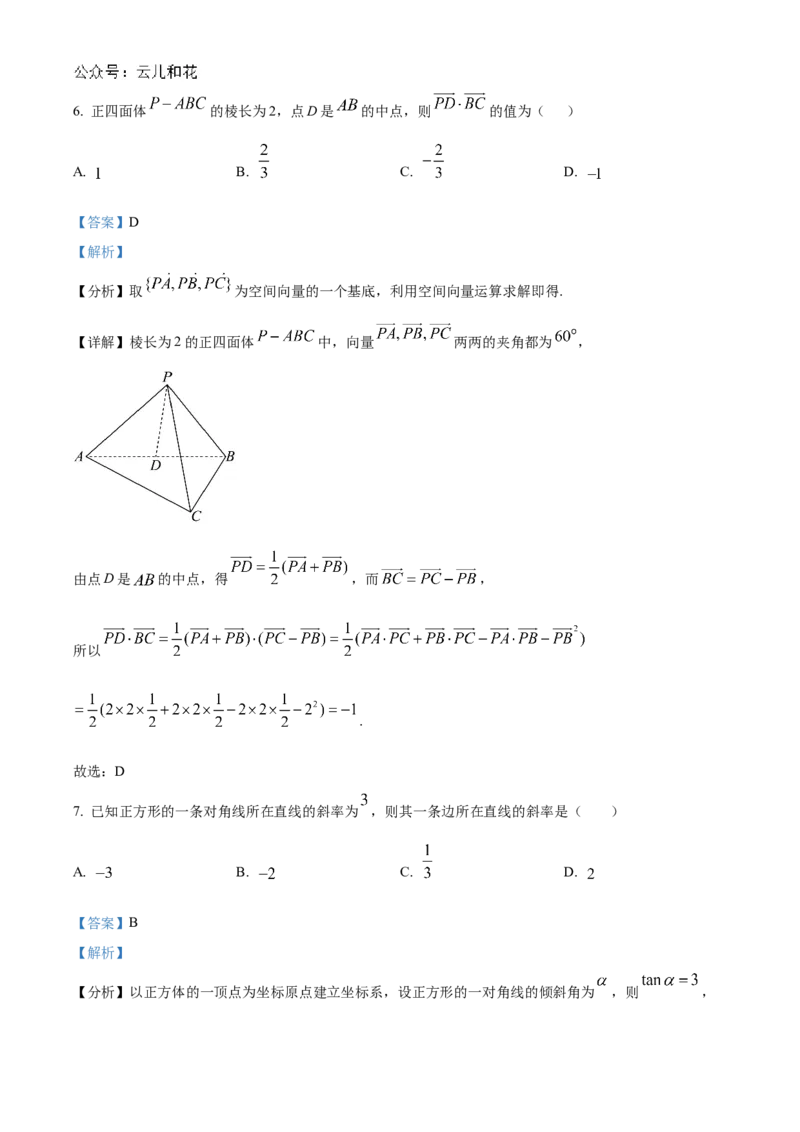
故选:C6. 正四面体 的棱长为2,点D是 的中点,则 的值为( )
A. B. C. D.
【答案】D
【解析】
【分析】取 为空间向量的一个基底,利用空间向量运算求解即得.
【详解】棱长为2的正四面体 中,向量 两两的夹角都为 ,
由点D是 的中点,得 ,而 ,
所以
.
故选:D
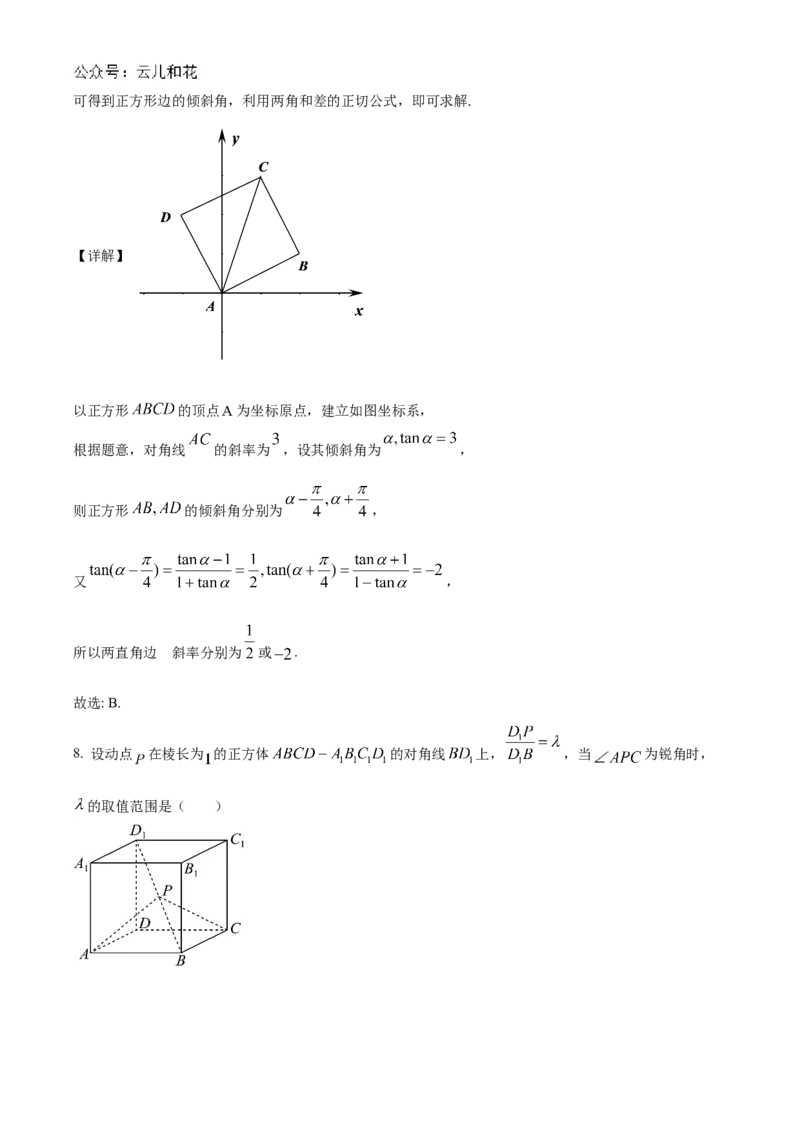
7. 已知正方形的一条对角线所在直线的斜率为 ,则其一条边所在直线的斜率是( )
A. B. C. D.
【答案】B
【解析】
【分析】以正方体的一顶点为坐标原点建立坐标系,设正方形的一对角线的倾斜角为 ,则 ,可得到正方形边的倾斜角,利用两角和差的正切公式,即可求解.
【详解】
以正方形 的顶点 为坐标原点,建立如图坐标系,
根据题意,对角线 的斜率为 ,设其倾斜角为 ,
则正方形 的倾斜角分别为 ,
又 ,
所以两直角边 的斜率分别为 或 .
故选: B.
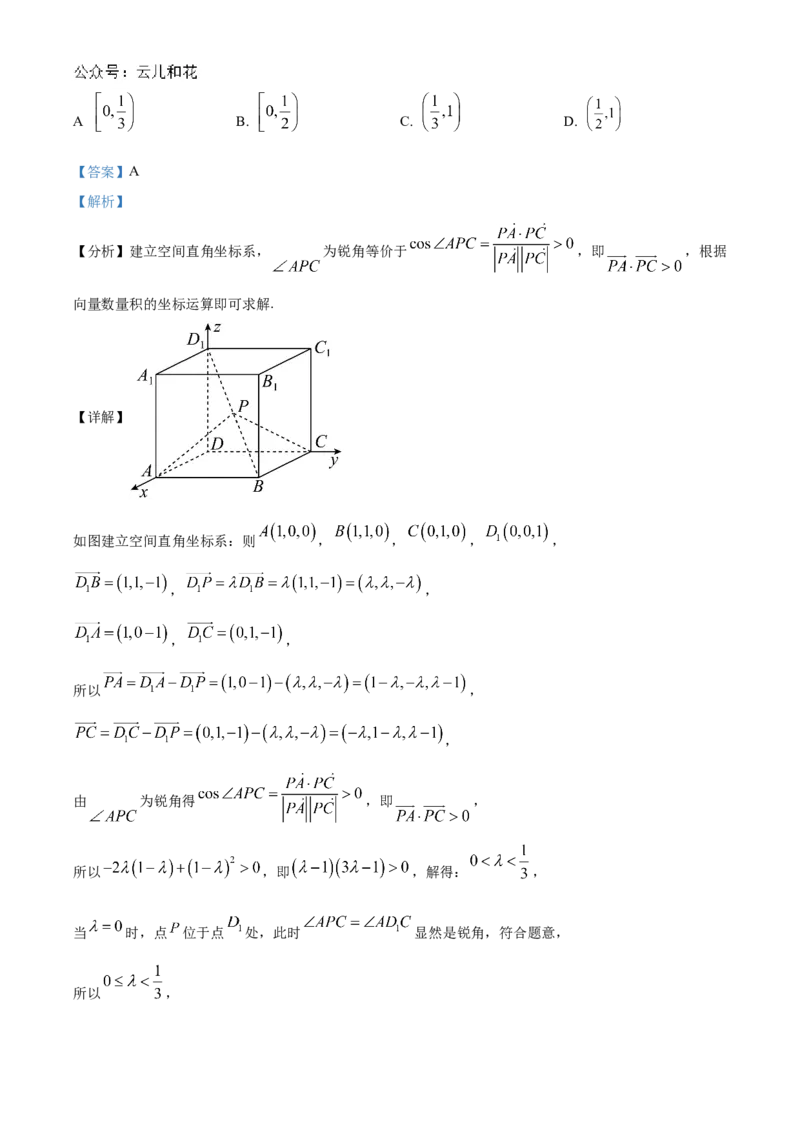
8. 设动点 在棱长为 的正方体 的对角线 上, ,当 为锐角时,
的取值范围是( ).
A B. C. D.
【答案】A
【解析】
【分析】建立空间直角坐标系, 为锐角等价于 ,即 ,根据
向量数量积的坐标运算即可求解.
【详解】
如图建立空间直角坐标系:则 , , , ,
, ,
, ,
所以 ,
,
由 为锐角得 ,即 ,
所以 ,即 ,解得: ,
当 时,点 位于点 处,此时 显然是锐角,符合题意,
所以 ,故选:A
【点睛】关键点点睛:本题的关键点是 为锐角等价于 ,即 ,
还需利用 , 求出⃑PA、 的坐标,根据向量数量积的坐标运算即可求
解.
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的四个选项中,有多项符合
题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9. 已知向量 , , ,则下列结论正确的是( )
A. 与 垂直 B. 与 共线
C. 与 所成角为锐角 D. , , ,可作为空间向量的一组基底
【答案】BC
【解析】
【分析】对A:计算出 即可得;对B:由向量共线定理计算即可得;对C:计算 并判断 与 是
否共线即可得;对D:借助空间向量基本定理即可得.
【详解】对A: ,故 与 不垂直,故A错误;
对B:由 、 ,有 ,故 与 共线,故B正确;
对C: ,且 与 不共线,
故 与 所成角为锐角,故C正确;
对D:由 与 共线,故 , , 不可作为空间向量的一组基底,故D错误.
故选:BC.
10. 已知两直线 , ,则下列说法正确的是( )A. 对任意实数m,直线 , 的方向向量都不可能平行
B. 存在实数m,使直线 垂直于x轴
C. 存在实数m,使直线 , 互相垂直
D. 当 时,直线 的方向向量不存在
【答案】AC
【解析】
【分析】根据直线平行以及垂直满足的系数关系,即可结合方向向量的定义逐一求解.
【详解】若两直线的方向向量平行,则 ,则 无实数解,故两直线的方向向量不可能平行,故
A正确,
由于 的斜率为 ,所以直线 不可能垂直于x轴,B错误,
当 时,此时 , ,此时两直线垂直,C正确,
当 时,直线 ,则其方向向量可以为 ,故D错误,
故选:AC
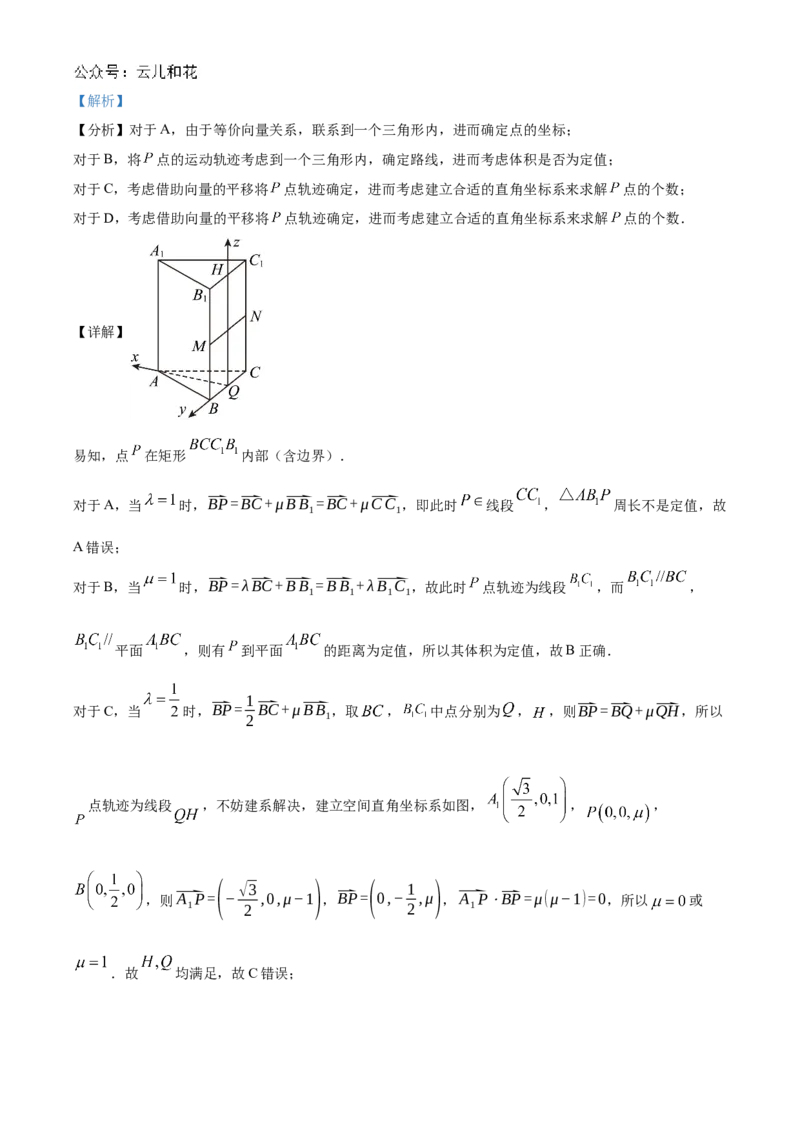
11. 在正三棱柱 中, ,点 满足⃑BP=λ⃑BC+μ⃑BB ,其中 ,
1
,则( )
A. 当 时, 的周长为定值
B. 当 时,三棱锥 的体积为定值
C. 当 时,有且仅有一个点 ,使得
D. 当 时,有且仅有一个点 ,使得 平面
【答案】BD【解析】
【分析】对于A,由于等价向量关系,联系到一个三角形内,进而确定点的坐标;
对于B,将 点的运动轨迹考虑到一个三角形内,确定路线,进而考虑体积是否为定值;
对于C,考虑借助向量的平移将 点轨迹确定,进而考虑建立合适的直角坐标系来求解 点的个数;
对于D,考虑借助向量的平移将 点轨迹确定,进而考虑建立合适的直角坐标系来求解 点的个数.
【详解】
易知,点 在矩形 内部(含边界).
对于A,当 时,⃑BP=⃑BC+μ⃑BB =⃑BC+μ⃑CC ,即此时 线段 , 周长不是定值,故
1 1
A错误;
对于B,当 时,⃑BP=λ⃑BC+⃑BB =⃑BB +λ⃑B C ,故此时 点轨迹为线段 ,而 ,
1 1 1 1
平面 ,则有 到平面 的距离为定值,所以其体积为定值,故B正确.
1
对于C,当 时,⃑BP= ⃑BC+μ⃑BB ,取 , 中点分别为 , ,则⃑BP=⃑BQ+μ⃑QH,所以
2 1
点轨迹为线段 ,不妨建系解决,建立空间直角坐标系如图, , ,
( √3 ) ( 1 )
,则⃑A P= − ,0,μ−1 ,⃑BP= 0,− ,μ ,⃑A P⋅⃑BP=μ(μ−1)=0,所以 或
1 2 2 1
.故 均满足,故C错误;1
对于D,当 时,⃑BP=λ⃑BC+ ⃑BB ,取 , 中点为 .⃑BP=⃑BM+λ⃑MN,所以 点轨
2 1
(√3 ) ( √3 1) ( √3 1 )
迹为线段 .设 ,因为A ,0,0 ,所以⃑AP= − ,y , ,⃑A B= − , ,−1 ,
2 2 0 2 1 2 2
所以 ,此时 与 重合,故D正确.
故选:BD.
【点睛】本题主要考查向量的等价替换,关键之处在于所求点的坐标放在三角形内.
第Ⅱ卷(非选择题 共92分)
三、填空题:本题共3小题,每小题5分,共15分.
12. 已知向量 , ,若 与 垂直,则 =_____.
【答案】
【解析】
【分析】根据给定条件,利用向量垂直关系求出x,再结合向量的坐标运算及模的运算计算作答.
【详解】向量 与 垂直,则有 ,解得 ,
于是 ,
所以 .
故答案为:
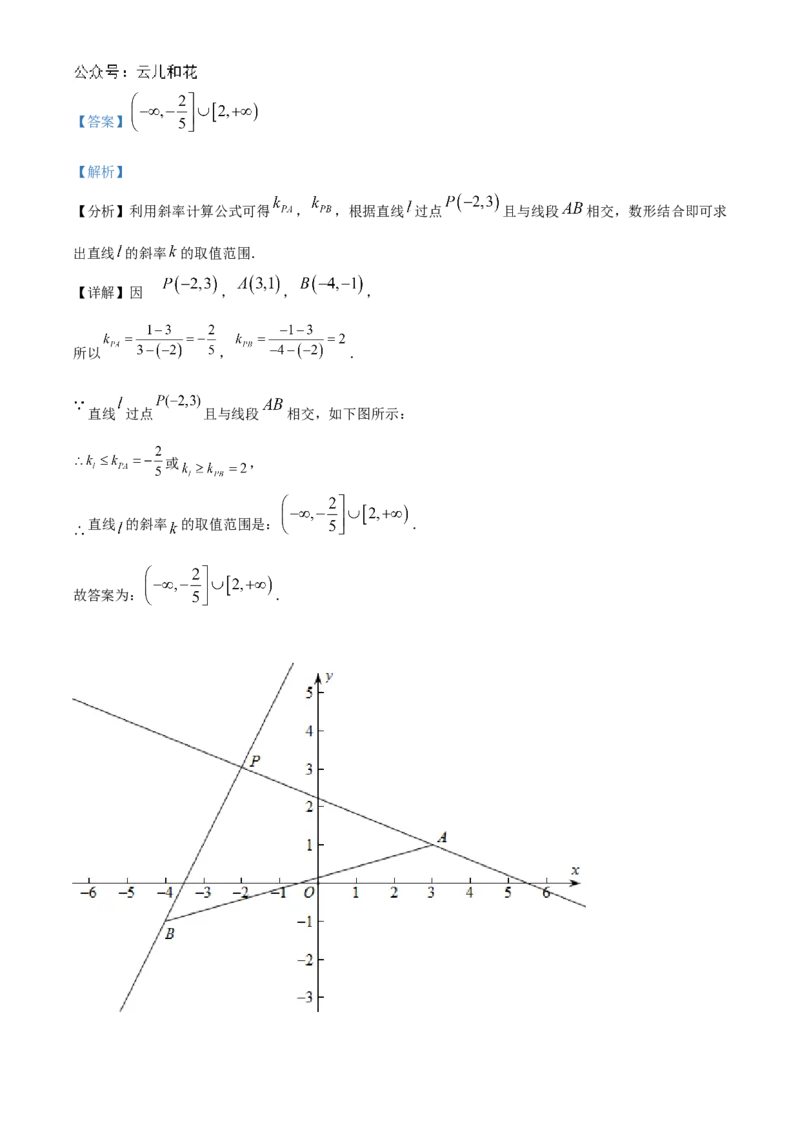
13. 已知点 , ,直线 是过点 且与线段AB相交且斜率存在,则 的斜率 的取
值范围是____________【答案】
【解析】
【分析】利用斜率计算公式可得 , ,根据直线 过点 且与线段 相交,数形结合即可求
出直线 的斜率 的取值范围.
【详解】因 为, , ,
所以 , .
直线 过点 且与线段 相交,如下图所示:
或 ,
直线 的斜率 的取值范围是: .
故答案为: .14. 在 中,已知 , 边上的高线所在的直线方程为 , 边上的高线所在的直
线方程为 .则 边所在的直线方程为_______.
【答案】
【解析】
【分析】由 边上和 边上的高线所在的直线方程,可得 边和 边所在直线的斜率,再由 点
坐标,可求 边和 边所在直线的方程,通过联立方程组,求出 两点的坐标,可求 边所在的
直线方程
【详解】 边上的高线所在的直线方程为 ,得 ,
边上的高线所在的直线方程为 ,得
已知 ,则AC边所在的直线方程为 ,即 ,
则AB边所在的直线方程为 ,即 .
由 ,得 .
由 ,得 .
则BC边所在的直线方程为 ,即 .
故答案为: .
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15. 已知空间中三点 ,设 .(1)若 ,且 ,求向量 ;
(2)求以 为一组邻边的平行四边形的面积 .
【答案】(1) 或
(2)
【解析】
【分析】(1)利用向量平行和向量模长的坐标表示列式求解即可;
(2)利用向量数量积和向量模长的坐标表示求出夹角进而求面积即可.
【小问1详解】
由 可得 ,
若 ,则 ,
又 ,所以 ,解得 ,
所以 或 .
【小问2详解】
由 可得 , ,
所以 , , ,
所以 ,所以 ,
所以 .
16. 如图,四棱锥 中, 平面ABCD,四边形ABCD是梯形, , ,
, ,点E是AP的中点,F是PB上的点, .(1)求证:点F在平面ECD内;
(2)求点P到平面ECD的距离.
【答案】(1)证明见解析
(2)
【解析】
【分析】(1)建立空间直角坐标系,利用空间向量的共面定理证明;
(2)利用空间向量的坐标运算求点到平面的距离.
【小问1详解】
因为 , ,所以 ,
又因为 平面ABCD, 平面ABCD,
所以 ,
所以如图所示,以 为坐标原点,建立空间直角坐标系 ,
则
所以 ,设
则 ,解得 ,所以
所以点F在平面ECD内.
【小问2详解】
设平面 的一个法向量为 ,
由(1)知
因为 ,所以 ,
令 ,则 ,所以 ,
又因为 ,
所以点P到平面ECD的距离 .
17. 已知直线l过点 ,O为坐标原点.
(1)若直线l在两坐标轴上的截距相等,求直线l方程;
(2)若直线l与x轴、y轴的正半轴分别交于A,B两点且 面积为24.
ⅰ)求直线l方程;ⅱ)若点P为线段AB上一动点,且 交OA于点Q.在y轴上是否存在点M,使 为等腰
直角三角形,若存在,求出点M的坐标;若不存在,说明理由.
【答案】(1) 或
(2)ⅰ) ,ⅱ) , ,
【解析】
【分析】(1)分类讨论截距是否为零,计算即可;
(2)利用截距式结合面积公式计算可得第一小问,利用等腰直角三角形的特征分类讨论计算即可.
【小问1详解】
若直线过原点,易知其方程为: ;
若直线不过原点,不妨设其方程为: ,
代入点 得 ,即 ;
【小问2详解】
i)由截距式设直线 的方程为 ,所以 ,
所以 ,即 ;
ⅱ)若存在 为等腰直角三角形,不妨设 , ,则 ,
因为 为等腰三角形,
当M为直角顶点时,设 , , ,
所以 ,即 ,所以 或 (舍),所以 ,即点 ;
当Q为直角顶点时,点 , ,符合题意;
当P为直角顶点时,设 ,由 可得: ,
所以 , ;
综上所以 , , ,符合题意.
18. 如图,在四棱锥 中,底面 是平行四边形, , 底面 ,
,E、F分别为BC、AD的中点,点M在线段 上.
(1)求证: 平面 ;
(2)设 ,若直线 与平面 所成的角 的正弦值为 ,求 的值.
【答案】(1)证明见解析
(2)
【解析】
【分析】(1)证明 , ,推出 ,然后证明 平面 ;
(2)建立空间直角坐标系,利用直线与平面所成角的向量法求解即可.【小问1详解】
在平行四边形 中,因为 , ,
所以 ,故 ,
由E、F分别为 的中点,得 ,所以 ,
因为 底面 , 底面ABCD,所以 ,
又因为 , 平面 , 平面 ,
所以 平面 .
【小问2详解】
因为 底面 , ,所以 两两垂直,
分别以 所在直线为x轴、y轴和z轴,建立如图所示的空间直角坐标系
则A(0,0,0),
所以 ,由已知 ,
即 ,所以
设平面 的一个法向量为 ,
由 ,得 ,
令 ,得 ,所以 ,
化简得 ,故 或 (舍).
所以 .
19. 球面三角学是研究球面三角形的边、角关系的一门学科.如图一,球 的半径为 , 为球面上
三点,劣弧 的弧长记为 ,设 表示以 为圆心,且过 的圆,同理,圆 , 的劣弧
的弧长分别记为 ,曲面 (阴影部分)叫做球面三角形,若设二面角 ,
, 分别为 , , ,则球面三角形的面积为 .
(1)若平面 ,平面 ,平面 两两垂直,求球面三角形 的面积;
(2)若将图一中四面体 截出得到图二,若平面三角形 为直角三角形, ,设
, , .
①求证: ;
②延长 与球 交于点 ,连接 ,若直线 与平面 所成的角分别为 , ,, , 为 中点, 为 中点,设平面 与平面 的夹角为 ,求
的最小值.
【答案】(1)
(2)①证明见解析;② .
【解析】
【分析】(1)根据平面 ,平面 ,平面 两两垂直,得 ,即可求解;
(2)①根据余弦定理及勾股定理即可证明;
②建立空间直角坐标系,分别求出平面 和平面 的法向量,利用向量夹角公式即可求解.
【小问1详解】
解:因为平面 ,平面 ,平面 两两垂直,
所以 ,
所以球面三角形ABC的面积 ;
【小问2详解】
解:①证明:由余弦定理可得:
,且 ,
所以 ,
即 ,
消去 ,则有:即 ;
②由题意可知 是球的直径,则有 ,
又 ,
所以 平面 ,
又因为 平面 ,
所以 ,
又因为 ,
所以 平面 , 平面 ,
所以 ,
又因为直线 与平面 所成的角分别为 , ,
所以 ,
不妨令 ,
则 , ,
又因为 , , ,
以 为坐标原点,以 所在直线为 轴,过点 作 的平行线为 轴,建立空间直角坐标系:
设 ,
则可得 ,
则 , ,
设平面 的一个法向量为 ,
则 ,
取 ,则 ,
所以 ;
设平面 的一个法向量为 ,
则 ,
取 ,则 ,
所以 ,
要使 取最小值,则 取最大值,
因为令 ,
则 ,
所以
当且仅当 时等号成立,
则 的最大值为 ,
所以 取最小值为 .
【点睛】方法点睛:在涉及求直线与平面、平面与平面所成角时,利用空间向量法求解更简单些.