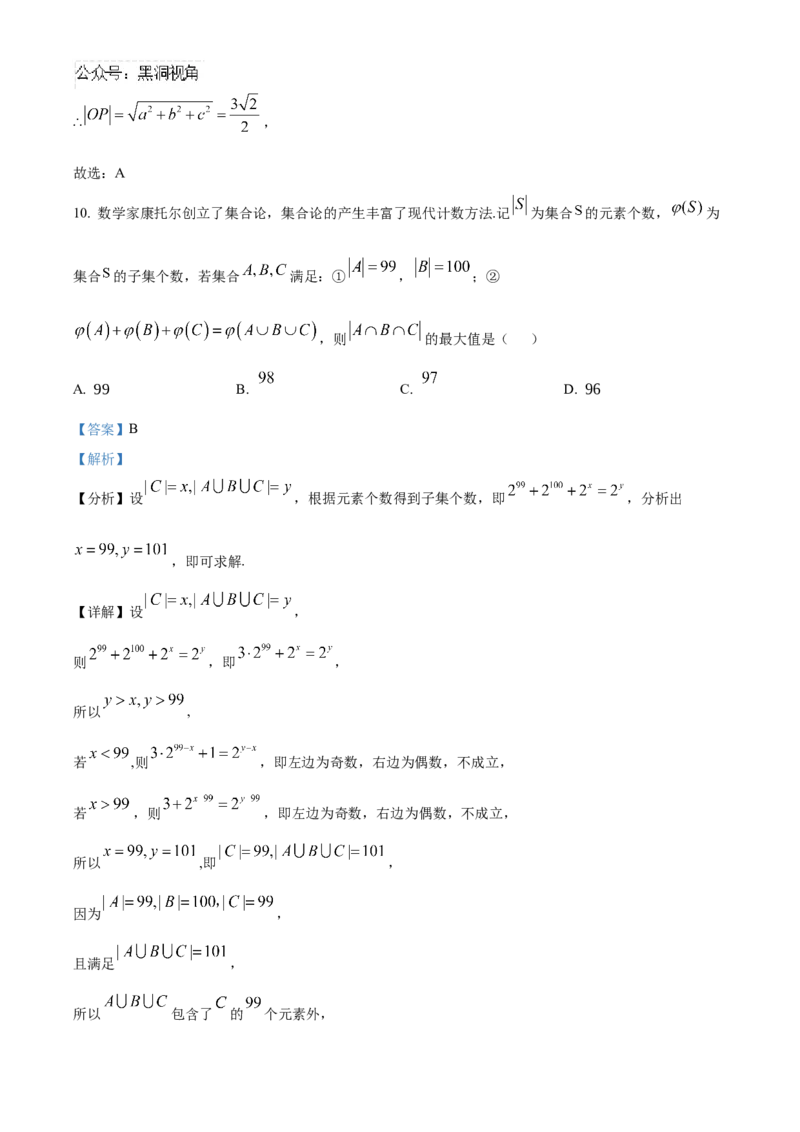文档内容
北京市朝阳区 2024~2025 学年度第一学期期中质量检测
高三数学试卷
2024.11
(考试时间120分钟 满分150分)
本试卷分为选择题40分和非选择题110分
第一部分(选择题 共40分)
一、选择题共10小题,每小题4分,共40分.在每小题列出的四个选项中,选出符合题目要
求的一项.
1. 设集合 ,集合 ,则 ( )
A. B.
C. D.
【答案】A
【解析】
【分析】根据集合的交集运算即可得答案.
【详解】因为集合 ,集合 ,
所以 .
.
故选:A
2. 若函数 在 处取得最小值,则 ( )
A. 1 B. C. 2 D. 4
【答案】C
【解析】
【分析】因为 ,所以用基本不等式求得最小值,并找到最小值点为 ,得出结果 .【详解】∵ ,∴ ,
∴ ,
当且仅当 ,即 时取等号,
∴最小值点 ,即 .
故选;C
3. 下列函数中,既是奇函数又在区间 上单调递增的是( )
A. B.
C. D.
【答案】D
【解析】
【分析】根据函数的奇偶性以及单调性,结合基本初等函数的性质,即可逐一判断.
【详解】对于A,函数 为指数函数,不具备奇偶性,故A错误;
对于B,函数 的定义域为 ,
由于 为偶函数,故B错误;
对于C,函数 ,由正切函数的性质可知 为奇函数,
且在 单调递增,故C错误;
对于D,函数 的定义域为 ,由 ,故函数 为奇函数,
因为 ,
所以函数 在 单调递增,故D正确.
故选:D.
4. 如图,在 中, , ,则( )
A. B.
C. D.
【答案】C
【解析】
【分析】由向量的线性关系即可得到结果.
【详解】∵ , ,
∴ , ,
∴ ,故AB选项错误;∴ ,故C选项正确,D选项错
误.
故选:C
5. 已知单位向量 , 满足 ,设向量 ,则向量 与向量 夹角的余弦值是( )
A. B. C. D.
【答案】C
【解析】
【分析】先算出 , ,再利用向量夹角公式即可得到答案
【详解】解: ,
,
所以 ,
故选:C.
6. 《九章算术》是我国古代数学名著,书中有如下的问题:“今有女子善织,日自倍,五日织五尺,问日
织几何?”意思是:“一女子善于织布,每天织的布都是前一天的2倍,已知她5天共织布5尺,问这女子
每天分别织布多少?”.由此推算,在这5天中,织布超过1尺的天数共有( )
A. 1天 B. 2天 C. 3天 D. 4天
【答案】B
【解析】
【分析】设这女子每天分别织布 尺,则数列 是等比数列,公比 .利用等比数列的通项公式及
其前 项和公式即可得出.
【详解】设这女子每天分别织布 尺,
则数列 是等比数列,公比 .则 ,解得 .
数列 的通项公式为 ,
,
当 时,则 ,
当 时,则 ,
故超过1尺的天数共有2天.
故选:B.
7. 已知 均为第二象限角,则“ ”是“ ”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
【答案】C
【解析】
【分析】结合三角函数的单调性、平方关系,并根据充分、必要条件的知识判断即可.
【详解】由题意, 若 ,因为 均为第二象限角,所以 ,
所以 ,即 ,
所以 ,且 均为第二象限角,
所以 ,所以 ,即充分性成立.
若 ,因为 均为第二象限角,
所以 ,即 ,所以 ,即 ,
因为 均为第二象限角,所以 ,
所以 ,故必要性成立,
所以“ ”是“ ”的充要条件.
故选:C.
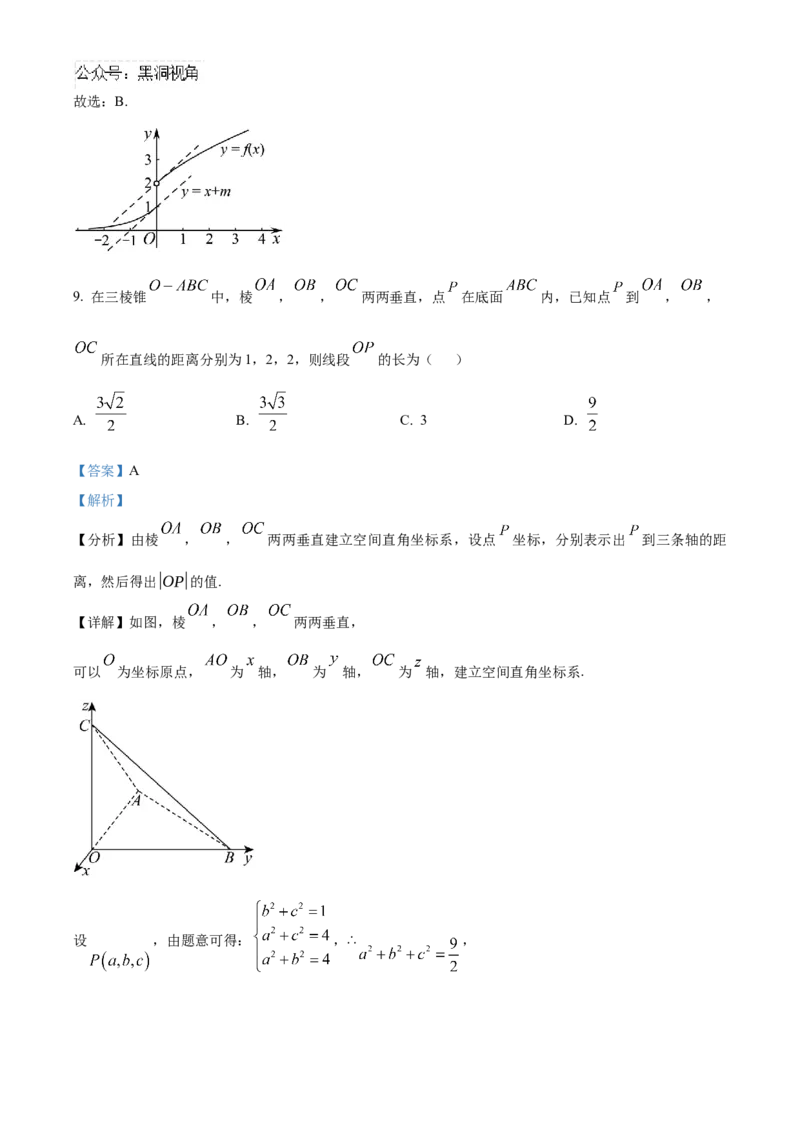
8. 已知函数 若直线 与函数 的图象有且只有一个公共点,则实
数 的取值范围是( )
A. B.
C. D.
【答案】B
【解析】
【分析】通过导数求出直线 与分段函数各段相切对应的 值,并结合图象即可求解.
【详解】当 时,函数 ,则 ,
令 ,解得 ,
故直线 与 相切,即 .
当 时,函数 ,则 ,
令 ,解得 ,
故直线 与 相切,即 .
如图所示,当 或 时,直线 与分段函数 有且仅有一个公共点.
故实数 的取值范围为 或 .故选:B.
9. 在三棱锥 中,棱 , , 两两垂直,点 在底面 内,已知点 到 , ,
所在直线的距离分别为1,2,2,则线段 的长为( )
A. B. C. 3 D.
【答案】A
【解析】
【分析】由棱 , , 两两垂直建立空间直角坐标系,设点 坐标,分别表示出 到三条轴的距
离,然后得出|OP|的值.
【详解】如图,棱 , , 两两垂直,
可以 为坐标原点, 为 轴, 为 轴, 为 轴,建立空间直角坐标系.
设 ,由题意可得: ,∴ ,∴ ,
故选:A
10. 数学家康托尔创立了集合论,集合论的产生丰富了现代计数方法.记 为集合 的元素个数, 为
集合 的子集个数,若集合 满足:① , ;②
,则 的最大值是( )
A. 99 B. C. D. 96
【答案】B
【解析】
【分析】设 ,根据元素个数得到子集个数,即 ,分析出
,即可求解.
【详解】设 ,
则 ,即 ,
所以 ,
若 ,则 ,即左边为奇数,右边为偶数,不成立,
若 ,则 ,即左边为奇数,右边为偶数,不成立,
所以 ,即 ,
因为 ,
且满足 ,
所以 包含了 的 个元素外,还包含 个属于 而不属于 的元素,
当 时,则 ,
如 ,符合题意.
当 时,则 ,
如 ,符合题意.
所以 的最大值为 ,
故选:B.
【点睛】关键点点睛:本题考查交集与并集的混合运算,及集合的元素个数与集合子集间的关系,解题的
关键由已知条件求 ,再分 和 讨论,体现了分类讨论的数学思想方法,难度较
大.
第二部分(非选择题 共110分)
二、填空题共5小题,每小题5分,共25分.
11. 复数 __________.
【答案】 ;
【解析】
【详解】 ,故答案为
12. 在 中,已知 ,则 __________; ________.
【答案】 ①. ## ②. ##
【解析】
【分析】根据同角三角函数关系,结合诱导公式即可求解.【详解】因为 , ,又 ,故 ;
.
故答案为: ; .
13. 已知数列 的前n项和为 (A,B为常数),写出一个有序数对 ________,
使得数列 是递增数列.
【答案】 (答案不唯一)
【解析】
【分析】根据数列的前n项和 与数列通项 的关系根据相减法即可得 的通项,再根据数列的单调
性可得 的范围,从而可得有序数对 的取值.
【详解】数列 的前n项和为 ,
当 时, ,
所以 ,
即 ,
当 时, 符合上式,
综上, ,
若数列 是递增数列,则 ,即 ,
故符合的有序数对 可以为 .故答案为: (答案不唯一).
14. 某种灭活疫苗的有效保存时间 (单位: )与储藏的温度 (单位:℃)满足函数关系 (
为常数,其中 ).已知该疫苗在0℃时的有效保存时间是1440h,在5℃时的有效保存时
间是360h,则该疫苗在10℃时的有效保存时间是________h.
【答案】90
【解析】
【分析】根据已知的函数模型以及已知数据,通过待定系数法即可求得结果.
【详解】由题意, ,
解得 ,
当 时, ,
故该疫苗在 时的有效保存时间是 小时.
故答案为: .
15. 对于无穷数列 ,若存在常数 ,使得对任意的 ,都有不等式
成立,则称数列 具有性质 . 给出下列四个结论:
①存在公差不为 的等差数列 具有性质 ;
②以 为首项, 为公比的等比数列 具有性质 ;
③若由数列 的前 项和构成的数列 具有性质 ,则数列 也具有性质 ;
④若数列 和 均具有性质 ,则数列 也具有性质 .的
其中所有正确结论 序号是________.
【答案】②③④
【解析】
【分析】对于①,可使用反证法证明①错误;对于②,取 ,并验证{a }具有性质 即可;
n
对于③和④,结合已知条件取适当的常数,并验证相应的数列具有性质即可.
【详解】对于①,假设存在公差为 的等差数列{a }具有性质 ,则存在常数 ,
n
使得对任意 的,都有不等式 成立.
则对任意的 ,都有 ,
但这对大于 的正整数 显然不成立,矛盾,故①错误;
对于②,设{a }是以 为首项, 为公比的等比数列,则 , .
n
所以正实数 满足对任意的 ,都有
.故②正确;
对于③,若由数列{a }的前 项和构成的数列 具有性质 ,则存在常数 ,
n
使得对任意的 ,都有不等式 成立.
从而正实数 满足对任意的 ,都有.故③正确;
对于④,若数列{a }和{b }均具有性质 ,存在常数 ,使得对任意的 ,
n n
都有不等式 成立;也存在常数 ,
使得对任意的 ,都有不等式 成立.
从而正实数 满足对任意的 ,都有
.故④正确.
故答案为:②③④
【点睛】关键点点睛:本题的关键在于理解性质 的定义,只有理解了定义,方可解决相应的问题.
三、解答题共6小题,共85分.解答应写出文字说明,演算步骤或证明过程.
16. 在 中, .
(1)求 的值;
(2)若 , ,求b及 的面积.【答案】(1)2 (2) ,
【解析】
【分析】(1)结合正弦定理边化角化简已知等式,再根据三角形中角度关系与正弦函数取值即可得结论;
(2)结合余弦定理求得 关系,从而可得 大小,再根据面积公式求解即可得答案.
【小问1详解】
因为 ,有正弦定理得 ,
所以 ,
由 ,得 ,
又因为 ,所以 , 所以 ,
由正弦定理可得 ;
【小问2详解】
因为 , ,
所以由余弦定理得 ,
又由(1)可知, ,所以 ,
整理得 ,即 ,
所以 , 所以 ,
所以 面积为 .
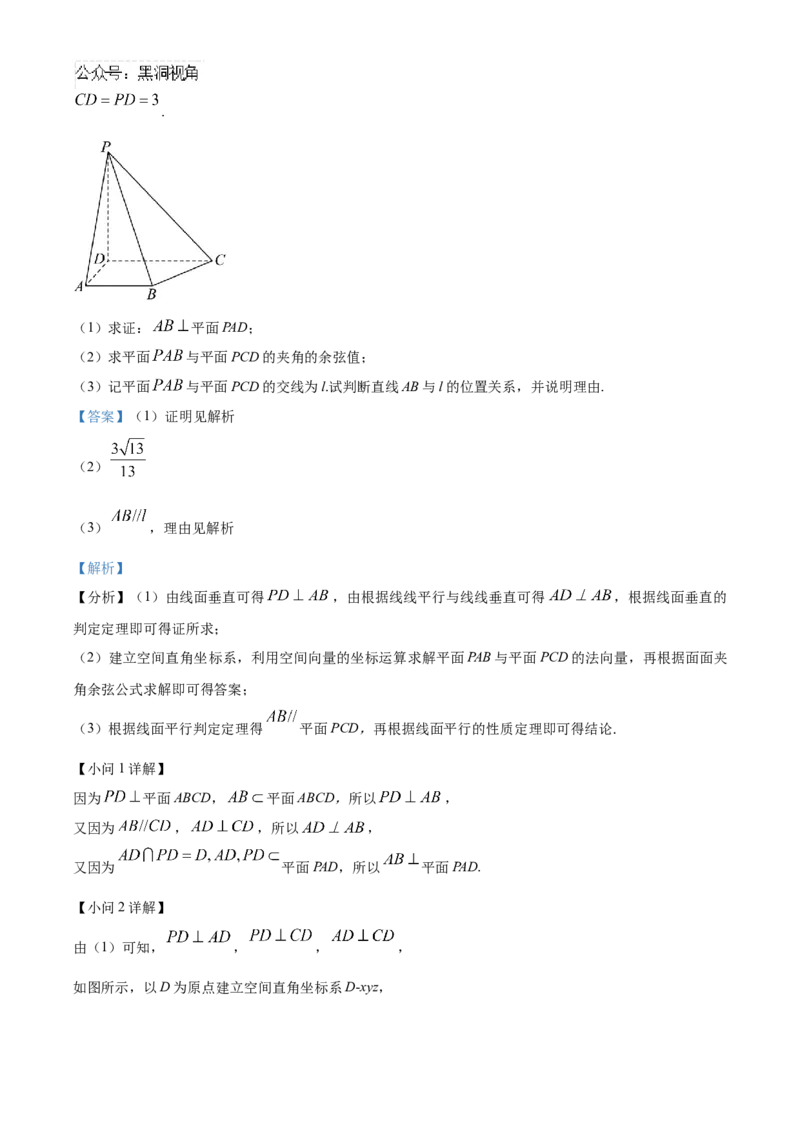
17. 如图,在四棱锥 中, 平面 , , , ,.
(1)求证: 平面PAD;
(2)求平面 与平面PCD的夹角的余弦值;
(3)记平面 与平面PCD的交线为l.试判断直线AB与l的位置关系,并说明理由.
【答案】(1)证明见解析
(2)
(3) ,理由见解析
【解析】
【分析】(1)由线面垂直可得 ,由根据线线平行与线线垂直可得 ,根据线面垂直的
判定定理即可得证所求;
(2)建立空间直角坐标系,利用空间向量的坐标运算求解平面PAB与平面PCD的法向量,再根据面面夹
角余弦公式求解即可得答案;
(3)根据线面平行判定定理得 平面PCD,再根据线面平行的性质定理即可得结论.
【小问1详解】
因为 平面ABCD, 平面ABCD,所以 ,
又因为 , ,所以 ,
又因为 平面PAD,所以 平面PAD.
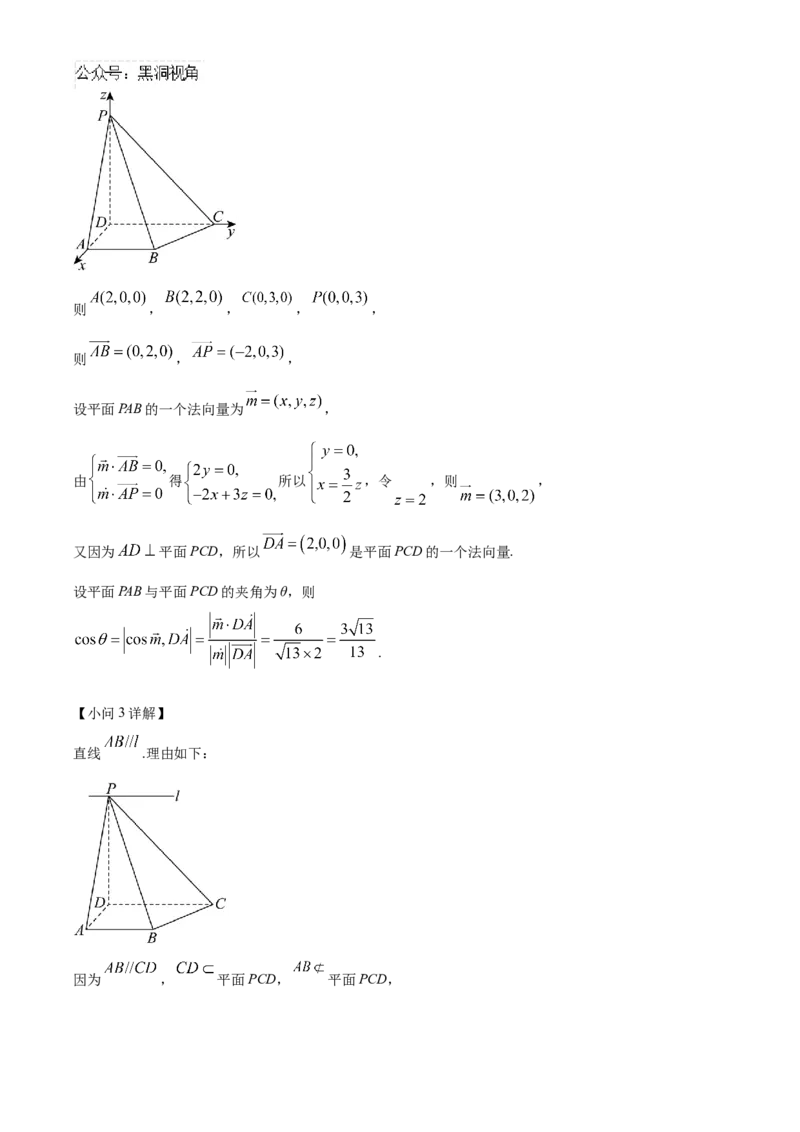
【小问2详解】
由(1)可知, , , ,
如图所示,以D为原点建立空间直角坐标系D-xyz,则 , , , ,
则 , ,
设平面PAB的一个法向量为 ,
由 得 所以 ,令 ,则 ,
又因为 平面PCD,所以 是平面PCD的一个法向量.
设平面PAB与平面PCD的夹角为θ,则
.
【小问3详解】
直线 .理由如下:
因为 , 平面PCD, 平面PCD,所以 平面PCD,
又因为 平面PAB,平面 平面 ,所以 .
18. 已知函数 .
(1)若 ,求 的最小值;
(2)若 存在极小值,求 的取值范围.
【答案】(1)
(2)
【解析】
【分析】(1)代入 ,得 ,求导并利用导函数判定函数的单调性,即可求得函数
的最值;
(2)先求导数,分类讨论 和 时函数 的单调性,并根据函数有极小值求解 的取值范围.
【小问1详解】
函数 的定义域为 ,
当 时, ,
时, , 在区间 上单调递减,
时, , 在区间 上单调递增.
所以当 时, 取得最小值 .
【小问2详解】
函数 的导函数为 .(1)当 时, , 在区间 上单调递减,
所以 无极值.
(2)当 时,令 ,得 .
当 变化时, 与 的变化情况如下表:
x
- 0 +
↘ 极小值 ↗
.
由上表知,当 时, 取得极小值
综上, 的取值范围为 .
19. 设函数 .
(1)若 , ,求 的值;
(2)已知 在区间 上单调递增,且 是函数 的图象的对称轴,再从条件①、条
件②、条件③这三个条件中选择一个作为已知,使函数 存在,求ω,φ的值.
条件①:当 时, 取到最小值;
条件②: ;条件③: 在区间 上单调递减.
注:如果选择的条件不符合要求,第(2)问得0分;如果选择多个符合要求的条件分别解答,按第一个解
答计分.
【答案】(1)
(2)答案见解析.
【解析】
【分析】(1)代入参数值得到函数关系,求函数值;
(2)先由三角恒等变换化简三角函数,选择条件①由函数图像的性质得到两条对称轴即可求出周期,从
而解出 的值,代入函数值求得 的值;选择条件③由函数图像的性质得到两条对称轴即可求出周期,从
而解出 的值,代入函数值求得 的值;选择条件②不能求出参数值,故不能选条件②.
【小问1详解】
由 , ,得 .
则 ;
【小问2详解】
,
,
.
选择条件①:
因为 在区间 上单调递增,
且 是函数 的图象的对称轴,又当 时, 取到最小值,所以 ,
故 .
因为 ,所以 .
所以 , .
又因为 ,
所以 ,得 .
又因为 ,所以 .
选择条件③:
因为 在区间 上单调递增,
且 是函数 的图象的对称轴,
又 在区间 上单调递减,所以 ,
故 .
因为 ,所以 .
所以 , .
又因为 ,所以 ,得 .
又因为 ,所以 .
选择条件②不能求出参数值,故不能选条件②.
20. 已知函数 .
(1)求曲线 在点 处的切线方程;
(2)讨论 在区间 上的零点个数;
(3)若 ,其中 ,求证: .
【答案】(1)
(2)1 (3)证明见解析
【解析】
【分析】(1)根据导数的几何意义分别求切点坐标与切线斜率,再根据直线的点斜式方程化简转化可得
所求;
(2)分当 和 两段分别确定函数的单调性与取值情况,从而判断每段函数零点个数,从而
得结论;
(3)设 ,求导确定函数 的单调性与取值情况,从而可得结论.
【小问1详解】
由 ,得 且 ,所以 ,
所以曲线 在 处的切线方程为: ,即 .
【小问2详解】
①当 时, , ,所以 .
所以 在区间 上无零点;②当 时, , ,所以 ,
所以 在区间 上单调递增,
又 , ,
所以 在区间 上仅有一个零点,
综上, 在区间 上的零点个数为1.
【小问3详解】
设 ,即 ,
所以 ,
设 , ,
因为 时, , ,所以 ,
所以 在区间 上单调递增,
即 在区间 上单调递增,
故 ,所以 在区间 上单调递增.
故 ,所以 .
因为 ,所以 ,
又 ,所以 .
21. 若有穷正整数数列A: , , ,…, 满足如下两个性质,则称数列A为T数列:①
;②对任意的 ,都存在正整数 ,使得.
(1)判断数列A:1,1,1,3,3,5和数列B:1,1,2,2,4,4,4,12是否为T数列,说明理由;
(2)已知数列A: , , ,…, 是T数列.
(i)证明:对任意的 , 与 不能同时成立;
(ii)若n为奇数,求 的最大值.
【答案】(1)数列A不是T数列,理由见解析
(2)(i)证明见解析;(ii)
【解析】
【分析】(1)根据T数列的定义分别验证条件①②即可判断数 是否为T数列;
(2)(i)利用反证法假设存在 ,使得 ,分别根据条件①②验证假
设,即可得结论;(ii)由条件①②可得 ,根据数列不等式以及数列求和即可得结论.
【小问1详解】
数列A不是T数列,理由如下:
对于数列A,因为 , ,且对任意的正整数 ,有
,
所以数列A不满足性质②,所以数列A不是T数列;
数列B是T数列,理由如下:
对于数列B,因为 , , , ,
所以数列B满足性质①,
又因为 , , , ,
, , ,所以数列B满足性质②.
所以数列B是T数列.
【小问2详解】
(i)假设存在 ,使得 ,
由性质①,可得 ,
由性质②,存在正整数 ,使得 ,
又因为 ,所以 ,故 ,
所以 ,
而 ,矛盾,
所以 与 不能同时成立;
(ii)由性质①,当 时,可得 ,
又因为 , 为正整数,所以 ,
由性质②,对任意的 ,有 ,
因为对任意 , ,
所以 ,
所以
,
当 , ,
( )时,上述不等式取到等号,且此时数列A满足①和②,是T数列,
综上, 的最大值为 .
【点睛】关键点点睛:本题关键是对“T数列”的定义与理解,证明部分关键是灵活运用反证法,求和部
分结合不等式的性质进行放缩处理.