文档内容
2024-2025 学年浙江省嘉兴市高二上学期期末测试数学试卷
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
π
1.经过点P(1,2)且倾斜角为 的直线方程是( )
2
A. x=1 B. x=2 C. y=1 D. y=2
2.在空间直角坐标系中,已知⃗ ,⃗ ,则 ⃗ ⃗ ( )
a=(−2,2,1) b=(2,0,−1) 2a−b=
A. (−2,4,1) B. (6,4,−3) C. (−6,4,3) D. (2,4,−1)
3.已知等差数列{a }的前n项和为S ,a =3,a +a =12,则S =( )
n n 1 2 3 5
A. 9 B. 15 C. 24 D. 35
4.抛物线x2=4 y的准线方程为( )
A. y=−2 B. y=−1 C. x=−2 D. x=−1
x2
5.已知椭圆C: + y2=1的左、右焦点分别为F ,F ,P为C上一点,满足PF ⊥PF ,则
4 1 2 1 2
|PF ||PF |=
( )
1 2
A. 1 B. 2 C. 3 D. 4
6.已知二面角α−l−β的大小为60∘,棱l上有A,B两点,线段AC与BD分别在这个二面角的两个半平面
内,并且线段AC与BD都垂直于l.若AB=5,AC=3,BD=6,则CD的长为( )
A. 2√13 B. 2√17 C. 2√21 D. 2√22
7.已知 , 为圆 上的两个动点,且 ,若直线 上存在点 ,且
A B C:(x−m) 2+ y2=4 |AB|=2√3 y=2x−m P
P为线段AB的中点,则实数m的取值范围是( )
A. [−2,2] B. [−√5,√5] C. [−2√3,2√3] D. [−2√5,2√5]
{a,a≥b,
8.定义max{a,b}= 若数列{a }的前n项和S =λn2+(10+λ)n(λ≠0,n∈N∗),数列{b }满足
b,a1,a a >1,(a −1)(a −1)<0.记T =a a a ⋯a ,则
n 1 100 101 100 101 n 1 2 3 n
下列结论正确的是( )
A. 00
100 102
C. T ≥T D. 使T <1成立的最小自然数n等于201
n 100 n
11.四棱锥 P−ABCD 的底面为正方形, PD⊥ 底面 ABCD , PD=1 , AD=√2 ,
P
⃗
M=λC
⃗
B
,
P
⃗
N=λA
⃗
B
,
其中λ≠0,下列说法正确的是( )
π
A. 存在实数λ,使得异面直线BP与MN的所成角为
3
1
B. 三棱锥B−MCD的体积为
3
√15
C. 直线PB与平面MCD所成角的正弦值的最大值为
5
π
D. 二面角B−MN−D的最大值为
2
三、填空题:本题共3小题,每小题5分,共15分。
12.在空间直角坐标系中,已知平面 的法向量为⃗ ,平面 的法向量为⃗ ,若
α a=(4,2,−2k) β b=(k−3,−1,1)
α//β,则实数k的值为 .
13.任取一个正整数,若是奇数,就将该数乘3再加上1;若是偶数,就将该数除以2.反复进行上述两种运算,
经过有限次步骤后,必进入循环圈1→4→2→1.这就是数学史上著名的“冰雹猜想”(又称“角谷猜想”
等).如取正整数m=8,根据上述运算法则得出8→4→2→1,共需经过3个步骤变成1(简称为3步“雹
第 页,共 页
2 1程”).现给出冰雹猜想的递推关系如下:已知数列{a }满足:a =m(m为正整数),
n 1
{ a
a = 2
n,当a
n
为偶数时,
当 m=20 时,使得 a =1 需要 步雹程.
n+1 n
3a +1,当a 为奇数时,
n n
14.已知抛物线 ,点 在 上, 为常数, 按照如下方式依次构造点
C:y2=2px(p>0) P (1,−2) C k k>0. Q
1 n−1
和P (n=2,3,⋯):过点P 作斜率为k的直线与C的另一交点为Q ,过点Q 作斜率为−k的直线与C
n n−1 n−1 n−1
的另一交点为P ,记P 的坐标为(x ,y ),Q 的坐标为(a ,b ),直线P P 的斜率为k ,则k b =
n n n n n n n n n+1 n 2025 2025
.
四、解答题:本题共5小题,共60分。解答应写出文字说明,证明过程或演算步骤。
15.(本小题12分)
在平面直角坐标系中,圆 经过点 ,且与圆 相切于点 .
C M(3,1) C :x2+ y2−2x−8 y+12=0 N(3,3)
1 2
(1)求直线C N的方程;
2
(2)求圆C 的标准方程.
1
16.(本小题12分)
π
如图,在直三棱柱ABC−A B C 中,∠BAC= ,AB=AC=2,BB =3,E为AB的中点,点F满足
1 1 1 2 1
⃗ ⃗
CF=λCC ,其中λ∈(0,1).
1
(1)若EF//平面A BC ,求λ的值;
1 1
第 页,共 页
3 11
(2)当λ= 时,求平面A BC 与平面AEF夹角的余弦值.
3 1 1
17.(本小题12分)
已知双曲线 x2 y2 的渐近线方程为 √2 ,点 在双曲线 上.
C: − =1(a>0,b>0) y=± x P(2,1) C
a2 b2 2
(1)求C的方程;
(2)过点M(−1,0)的直线l交双曲线C的左支于A,B两点,记直线PA,PB的斜率分别为k ,k ,是否存
1 2
在常数λ,使得k +k =λk k 恒成立?若存在,求λ的值;若不存在,请说明理由.
1 2 1 2
18.(本小题12分)
已知 为等差数列, , ,记
{a } a =6 a =15 b =a (n∈N∗).
n 2 5 n 3n
(1)求数列{a },{b }的通项公式;
n n
(2)在b 与b 之间插入n个数,使这n+2个数组成一个公差为d 的等差数列,
n n+1 n
1
(ⅰ)求数列{ }的前n项和T ;
d n
n
(ⅱ)在数列{d }中是否存在3项d ,d ,d (其中m,k,p成等差数列)成等比数列?若存在,求出这样的3
n m k p
项;若不存在,请说明理由.
19.(本小题12分)
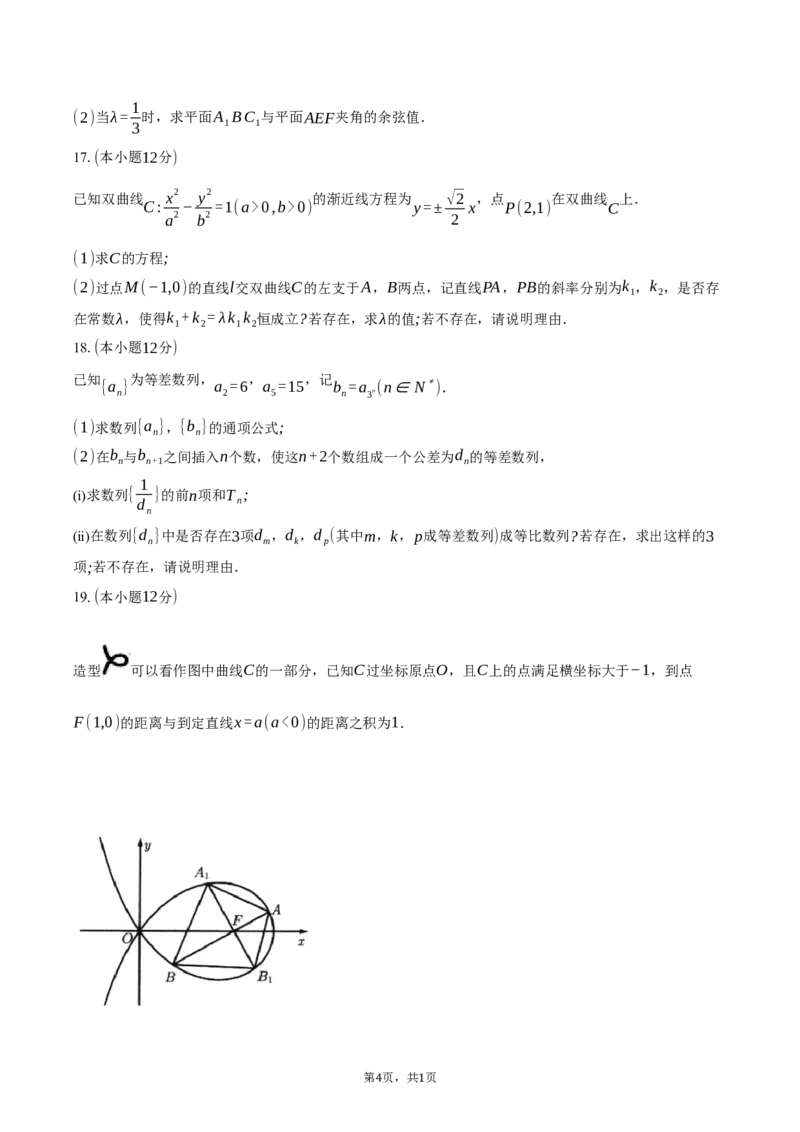
造型 可以看作图中曲线C的一部分,已知C过坐标原点O,且C上的点满足横坐标大于−1,到点
F(1,0)的距离与到定直线x=a(a<0)的距离之积为1.
第 页,共 页
4 1(1)求a的值;
−1
(2)当点(x ,y )在C上时,求证:y ≥ ;
0 0 0 x +1
0
(3)如图,过点F作两条互相垂直的弦,分别交曲线C于A(x ,y ),B(x ,y ),A (x ,y ),B (x ,y ),
1 1 2 2 1 3 3 1 4 4
其中x ≥0(i=1,2,3,4),求四边形A A BB 面积的最小值.
i 1 1
第 页,共 页
5 1参考答案
1.A
2.C
3.D
4.B
5.B
6.A
7.B
8.B
9.ABD
10.AD
11.BCD
12.1
13.7
14.−2
15.解: 把圆 化为标准方程,
(1) C :x2+ y2−2x−8 y+12=0
2
1
(x−1) 2+(y−4) 2=29,得圆心C (1,4),k =− ,
2 C 2 N 2
1
则直线C N:y−3=− (x−3),即x+2y−9=0.
2 2
方法一:设圆 的方程为 ,
(2) C (x−a) 2+(y−b) 2=r2 (r>0)
1
则
{(3−a) 2+(1−b) 2=r2,
(3−a) 2+(3−b) 2=r2,
两式相减得8−4b=0,则b=2,又因为a+2b−9=0,
所以 ,故所求圆 的方程为 .
a=5 C (x−5) 2+(y−2) 2=5
1
方法二:圆心C 线段MN的中垂线方程为y=2,
1
则圆心C 在直线y=2上,
1
第 页,共 页
6 1也在直线C N:x+2y−9=0上,
2
解得圆心C (5,2),
1
圆 的半径 ,
C r=|C M|=√5
1 1
圆 的标准方程 .
C (x−5) 2+(y−2) 2=5
1
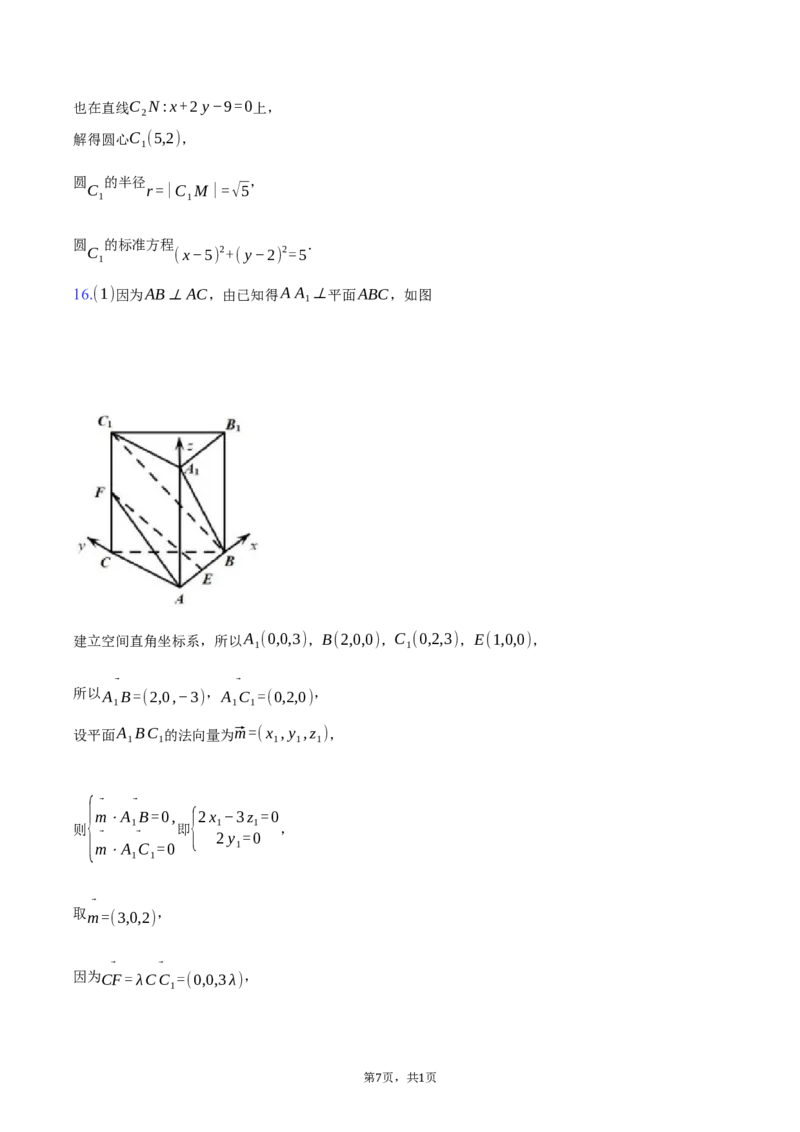
16.(1)因为AB⊥AC,由已知得A A ⊥平面ABC,如图
1
建立空间直角坐标系,所以A (0,0,3),B(2,0,0),C (0,2,3),E(1,0,0),
1 1
⃗ ⃗
所以A B=(2,0,−3) ,A C =(0,2,0) ,
1 1 1
设平面A BC 的法向量为⃗m=(x ,y ,z ),
1 1 1 1 1
{⃗ ⃗
m⋅A B=0, {2x −3z =0
1 1 1
则 即 ,
⃗ ⃗ 2y =0
m⋅A C =0 1
1 1
⃗
取m=(3,0,2) ,
⃗ ⃗
因为CF=λCC =(0,0,3λ) ,
1
第 页,共 页
7 1⃗
所以F(0,2,3λ),EF=(−1,2,3λ) ,
因为EF//平面A BC ,
1 1
⃗ ⃗
所以 EF⋅m=−3+6λ=0 ,
1
则λ= .
2
1
(2)因为λ=
3
,所以F(0,2,1),A ⃗ E=(1,0,0) ,⃗AE=(0,2,1),
设平面AEF的法向量为⃗n=(x ,y ,z ),
2 2 2
{⃗
n⋅A
⃗
E=0, { x =0
2
则 即 ,
⃗ ⃗ 2y +z =0
n⋅AF=0 2 2
⃗
取向量n=(0,1,−2) .
设平面A BC 与平面AEF所成角为θ,
1 1
| ⃗ ⃗ |
m⋅n 4 4√65
则cosθ= = = .
⃗ √13×√5 65
|m||n|
4√65
所以平面AB C 与平面DBE所成角的余弦值为 .
1 1 65
17.
{ b = √2 ,
解: 由已知得 a 2 解得 , ,
(1) a=√2 b=1
4 1
− =1,
a2 b2
第 页,共 页
8 1x2
所以双曲线C的方程为 −y2=1.
2
(2)设A(x ,y ),B(x ,y ),由题意知直线l的斜率不为0,设直线l的方程为x=my−1,
1 1 2 2
{
m2−2≠0,
{x2
联立
2
−y2=1,
消x得(m2−2)y2−2my−1=0,
Δ=4m2+4(m2−2)>0,
−1
x=my−1, y y = >0,
1 2 m2−2
解得10,
π −1
θ∈(0, ),则直线AB的方程为y=k(x−1),其中k=tanθ,直线A B 的方程为y= (x−1),
2 1 1 k
{(x+1) 2 [(x−1) 2+ y2 ]=1,
联立
y=k(x−1),
化简得到(1+k2 )x4−2(1+k2 )x2+k2=0,
{
x2+x2=2,
1 2
所以 k2
x 2x2=
1 2 1+k2
k tanθ
则x x = = =sinθ,
1 2 √1+k2 √1+tan2θ
故|x −x |=√x2+x2−2x x =√2−2sinθ,
1 2 1 2 1 2
第 页,共 页
12 1√ sin2θ √2−2sinθ √ 2
|AB|=√1+k2|x −x |= 1+ √2−2sinθ= = ,
1 2 cos2θ cos2θ 1+sinθ
2 √ 2
|A B |= =
同理 1 1 √ π 1+cosθ,所以
1+sin(θ+ )
2
1 1
S = |AB||A B |= ,
AA 1 BB 1 2 1 1 √1+sinθ+cosθ+sinθcosθ
令y=1+sinθ+cosθ+sinθcosθ,
π
令t=sinθ+cosθ=√2sin(θ+ ),
4
π
因为θ∈(0, ),
2
t2−1
所以t∈(1,√2],t2=1+2sinθcosθ,即sinθcosθ= ,
2
t2 1 π 3+2√2
所以y= +t+ 在(1,√2]上单调递增,当t=√2,即θ= 时,y = ,
2 2 4 max 2
√ 2 √2
此时S = =√2(3−2√2)=2−√2< ,
AABB 3+2√2 2
综上所述四边形A A BB 面积的最小值为2−√2.
1 1
第 页,共 页
13 1