2024学年第一学期质量检测高二数学试卷_2024-2025高二（7-7月题库）_2024年11月试卷_1107浙江省宁波市余姚中学2024-2025学年高二上学期10月月考

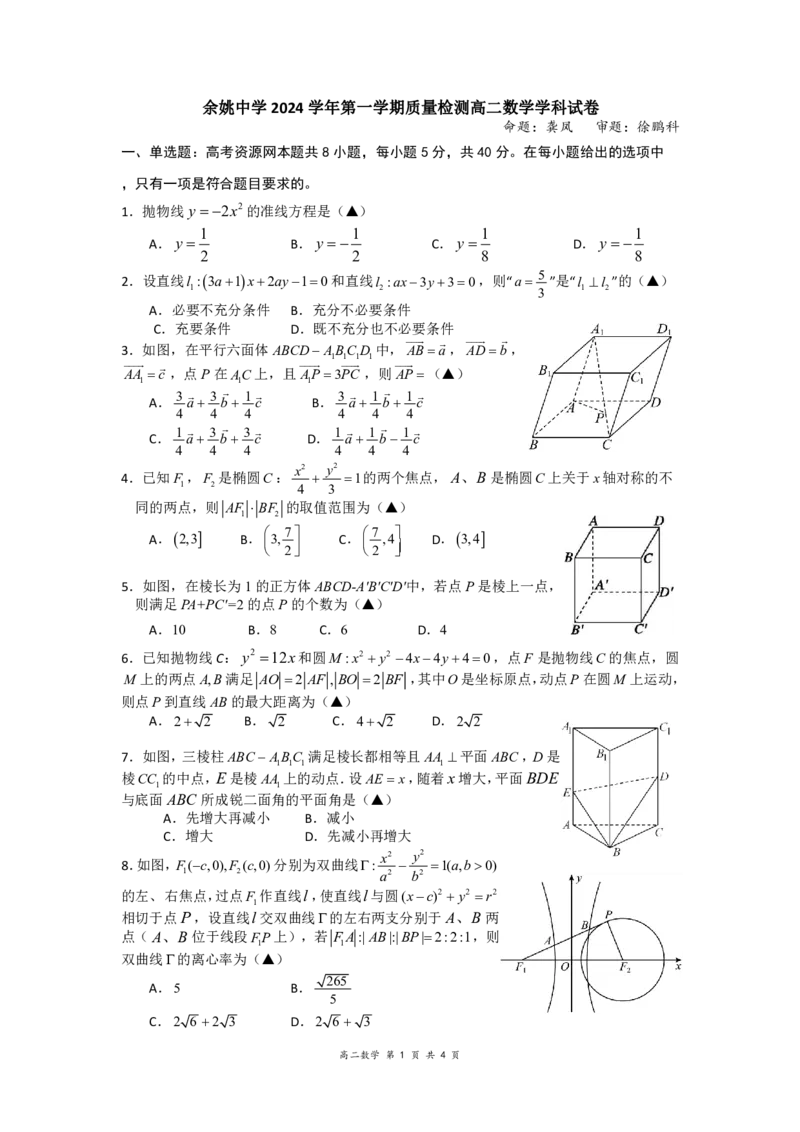
余姚中学 2024 学年第一学期质量检测高二数学学科试卷 命题：龚凤 审题：徐鹏科 一、单选题：高考资源网本题共8小题，每小题5分，共40分。在每小题给出的选项中 ，只有一项是符合题目要求的。 1．抛物线 y 2x2的准线方程是（▲） 1 1 1 1 A． y  B． y  C． y  D．y  2 2 8 8 2．设直线l :3a1x2ay10和直线l :ax3y30，则“a 5 ”是“l l ”的（▲） 1 2 3 1 2 A．必要不充分条件 B．充分不必要条件 C．充要条件 D．既不充分也不必要条件     3．如图，在平行六面体ABCDABCD 中，ABa，ADb， 1 1 1 1      AA c ，点P在AC上，且AP3PC ，则AP（▲） 1 1 1 3  3  1  3  1  1  A． a b c B． a b c 4 4 4 4 4 4 1  3  3  1  1  1  C． a b c D． a b c 4 4 4 4 4 4 4．已知F ，F 是椭圆C： x2  y2 1的两个焦点，A、B是椭圆C上关于x轴对称的不 1 2 4 3 同的两点，则 AF  BF 的取值范围为（▲） 1 2 A．2,3  B．  3, 7 C．   7 ,4  D．3,4   2   2  5．如图，在棱长为1的正方体ABCD-A'B'C'D'中，若点P是棱上一点， 则满足PA+PC'=2的点P的个数为（▲） A．10 B．8 C．6 D．4 6．已知抛物线C： y2 12x和圆M :x2  y2 4x4y40，点F 是抛物线C的焦点，圆 M 上的两点A,B满足 AO 2 AF , BO 2 BF ，其中O是坐标原点，动点P在圆M 上运动， 则点P到直线AB的最大距离为（▲） A．2 2 B． 2 C．4 2 D．2 2 7．如图，三棱柱ABC ABC 满足棱长都相等且AA 平面ABC，D是 1 1 1 1 棱CC 的中点，E是棱AA 上的动点．设AE x，随着x增大，平面BDE 1 1 与底面ABC 所成锐二面角的平面角是（▲） A．先增大再减小 B．减小 C．增大 D．先减小再增大 x2 y2 8．如图，F(c,0),F (c,0)分别为双曲线:  1(a,b0) 1 2 a2 b2 的左、右焦点，过点F 作直线l，使直线l与圆(xc)2  y2 r2 1 相切于点P，设直线l交双曲线的左右两支分别于A、B两 点（A、B位于线段FP上），若 FA:|AB|:|BP|2:2:1，则 1 1 双曲线的离心率为（▲） 265 A．5 B． 5 C．2 6 2 3 D．2 6  3 高二数学 第 1 页 共 4 页二、多选题：本题共3小题，共18分。在每小题给出的选项中，有多项符合题目要求。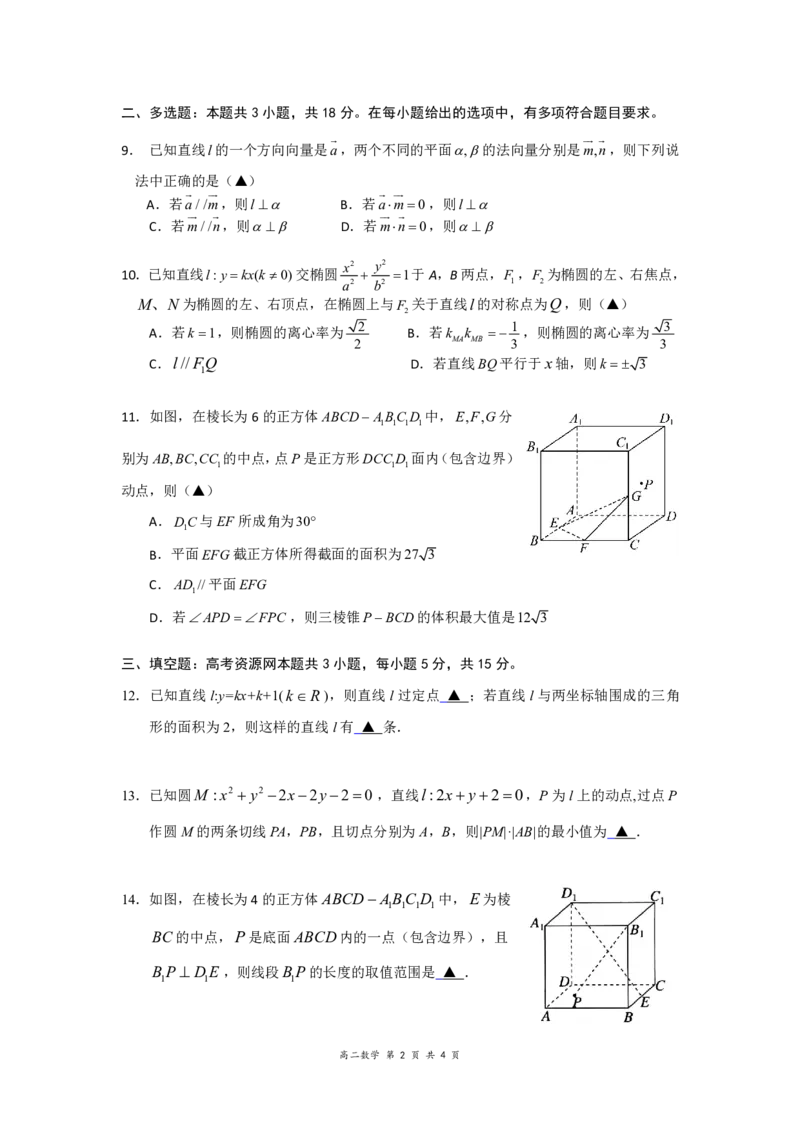    9． 已知直线l的一个方向向量是a，两个不同的平面,的法向量分别是m,n，则下列说 法中正确的是（▲）     A．若a//m，则l B．若am0，则l     C．若m//n，则 D．若mn0，则 x2 y2 10．已知直线l:ykx(k 0)交椭圆  1于A，B两点，F ，F 为椭圆的左、右焦点， a2 b2 1 2 M、N 为椭圆的左、右顶点，在椭圆上与F 关于直线l的对称点为Q，则（▲） 2 2 1 3 A．若k 1，则椭圆的离心率为 B．若k k  ，则椭圆的离心率为 2 MA MB 3 3 C．l//FQ D．若直线BQ平行于x轴，则k  3 1 11．如图，在棱长为6的正方体ABCDABCD 中，E,F,G分 1 1 1 1 别为AB,BC,CC 的中点，点P是正方形DCC D 面内（包含边界） 1 1 1 动点，则（▲） A．DC与EF 所成角为30 1 B．平面EFG截正方体所得截面的面积为27 3 C．AD //平面EFG 1 D．若APDFPC ，则三棱锥PBCD的体积最大值是12 3 三、填空题：高考资源网本题共3小题，每小题5分，共15分。 12．已知直线l:y=kx+k+1(kR)，则直线l过定点 ▲ ；若直线l与两坐标轴围成的三角 形的面积为2，则这样的直线l有 ▲ 条． 13．已知圆M :x2  y2 2x2y20 ，直线l:2x y20，P为l上的动点,过点P 作圆M的两条切线PA，PB，且切点分别为A，B，则|PM|·|AB|的最小值为 ▲ ． 14．如图，在棱长为4的正方体ABCDABC D 中，E为棱 1 1 1 1 BC的中点，P是底面ABCD内的一点（包含边界），且 BP  DE，则线段BP的长度的取值范围是 ▲ ． 1 1 1 高二数学 第 2 页 共 4 页四、解答题：本题共5小题，共77分。解答应写出文字说明、证明过程或演算步骤。 （本小题13分） 15. 已知圆C：x32 y42 4，点P(5，1)，点Q(1，2). （1）过点P作圆C的切线l，求出l的方程； （2）设A为圆C上的动点，G为三角形APQ的重心，求动点G的轨迹方程. 16．（本小题15分） 如图，在梯形ABCD中，AB∥CD， ADDC CB1， ABC 60，四边形ACFE为矩形，平面ACFE 平面ABCD， CF 1，点M 是线段EF 的中点． （1）求平面MAB与平面EAD所成锐二面角的余弦值； （2）求出直线CD到平面MAB的距离d ． 17．（本小题15分） 1 已知平面内两个定点A(2,0)，B(2,0)，满足直线PA与PB的斜率之积为 的动点P的 4 轨迹为曲线C，直线l与曲线C交于不同两点M，N . （1）求曲线C的轨迹方程； 1 （2）若直线AM 和AN的斜率之积为 ，试证明直线l过定点，并求出这个定点坐标. 12 高二数学 第 3 页 共 4 页．（本小题17分）   18 图1是直角梯形ABCD，AB//CD，D90，AB2，DC3，AD 3，CE 2ED， 以BE为折痕将△BCE折起，使点C到达C 的位置，且AC  6，如图2． 1 1 （1）求证：平面BCE平面ABED； 1 6 （2）在棱DC 上是否存在点P，使得点C 到平面PBE的距离为 ？若存在，求出二面 1 1 2 角PBEA的大小；若不存在，说明理由． ．（本小题17分） 19 已知椭圆C: x2  y2 1ab0的焦距为2，且过点  1, 3 ． a2 b2  2 （1）求椭圆C的方程； （2）记F 和F 分别是椭圆C的左、右焦点．设D是椭圆C上一个动点且纵坐标不为0． 1 2 直线DF交椭圆C于点A（异于D），直线DF 交椭圆C于点B（异于D）．若线段AB的 1 2 中点为M ，求三角形FF M 面积的最大值． 1 2 高二数学 第 4 页 共 4 页