2023学年顺德区普通高中教学质量检测（一）数学参考答案(1)_2023年11月_0211月合集_2024届广东省顺德区高三上学期教学质量检测（一）

2023 学年顺德区普通高中教学质量检测（一） 高三数学参考答案 2023．11 一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合 题目要求的． 1．C【解析】因为全集U {xZ ||x4|5}{1,0,1,2,3,4,5,6,7,8,9}，所以C A{1,0,2,4,6}， U 故答案选C． 2．D【解析】因为z是纯虚数，故设zbi(bR且b0)，又因为(z2)2 8i4b2 (4b8)i是纯虚数， 所以4b2 0且4b80，解得：b2，所以z2i，故答案选D． 3．C【解析】因为 f(x) axb ，所以 f(1) ab ．因为函数 f (x)在点(1, f (1))处的切线与直线 ab 1 1 x y10垂直，所以 f(1)1，即ab 1，所以ab( )2  ，当且仅当a b  时 2 4 2 等号成立，故答案选C．  1 1  2 1 2 1  2 1  1 1 1 4．A【解析】因为AE  AC AB，所以AE  AC  AB  ABAC  9 9 3 2 6 4 36 6 4 36 6  3，所以| AE| 3，故答案选A． x2  y2 6x40 x1 x6 5．B【解析】联立 ，解得： 或 ，所以圆M 的半径为： x2  y2 6y280 y 3 y 2 11 2 32 2 5，所以M 的面积为25，故答案选B． 3b 3b 6．A【解析】由题意可知F( 3,0)，准线l的方程为：x 3，所以A( 3, )，B( 3, )， a a 因为ABF 是正三角形，ABF 的高为焦点F( 3,0)到准线l的距离，即2 3，所以ABF 的边 2 3b b 2 3 c c2 a2 b2 长为4，所以| AB|4，所以 4，即  ，所以双曲线的离心率e   a a 3 a a2 a2 b2 7 21  1   ，故答案选A． a2 3 3 4 2tan 4 1 7．A【解析】因为tan2 ，所以  ，解得tan 或者tan2，因为 3 1tan2 3 2 3   cos( ) cos( ) cos( )  4 4 4 ( ,)，所以tan2，所以      2 sin( ) sin( ) sin( ) 4 4 4 高三数学试卷 第 1 页（共 8 页） {#{QQABCYCEogCgAAJAAAgCUwHCCECQkAGCAIoGAFAEsAABQBFABAA=}#}1  1tan 1    ，故答案选A． tan( ) tan1 3 4 8．D【解析】由 f(x1)2为奇函数得： f(x1) f(x1)4，即 f(x) f(2x)4，又因 为 f(x1)=f(3x)，所以 f(x2)=f(2x)，所以 f(x) f(x2)4，所以 f(x+2) f(x4） =4，两式相减得： f(x) f(x4)，所以函数 f(x)的周期T 4，所以 f(2023) f(3)，因为 f(x1)2为奇函数，所以 f(01)2=0，即 f(1)=2，在 f(x1) f(3x)0中，令x 0得： f(3) f(1)2，所以 f(2023) f(3)2，故答案选D． 二、多项选择题：本题共4小题，每小题5分，共20分．在每小题给出的四个选项中，有多项符合题目 要求．全部选对的得5分，部分选对的得2分，有选错的得0分． 0104 9．ABC【解析】甲机床次品数据的平均数为x  2， 甲 10 1 方差为D  [(02)2 (22)2 (42)2]1.6； 甲 10 131 乙机床次品数据的平均数为 y  1， 乙 10 1 方差为D  [(11)2 (31)2 (11)2]0.8． 乙 10 比较发现乙机床次品数据的平均数较小而且方差也较小，说明乙机床生产的次品数比甲机床生产的次 品数少，而且更为稳定，所以乙机床的性能较好，故答案ABC正确，D错误． 10．AD【解析】因为S 4S 4S 16，S 4S 4S 32，故A正确； 3 2 1 4 3 2 因为a 2a S S 2(S S )0，故B错误；因为4S S 4S (n2)， 3 2 3 2 2 1 n n1 n1 即S 4S 4S (n2)，所以S 2S 2(S 2S )2(S 2S )0 ， n1 n n1 n1 n n n1 2 1 S S 8 所以S 2S 0，即 n1 2，又因为 2  2，所以S 是以2为公比的等比数列， n1 n n S S 4 n 1 4,n1 所以S 42n1 2n1，所以a  ，故D正确． n n 2n,n2 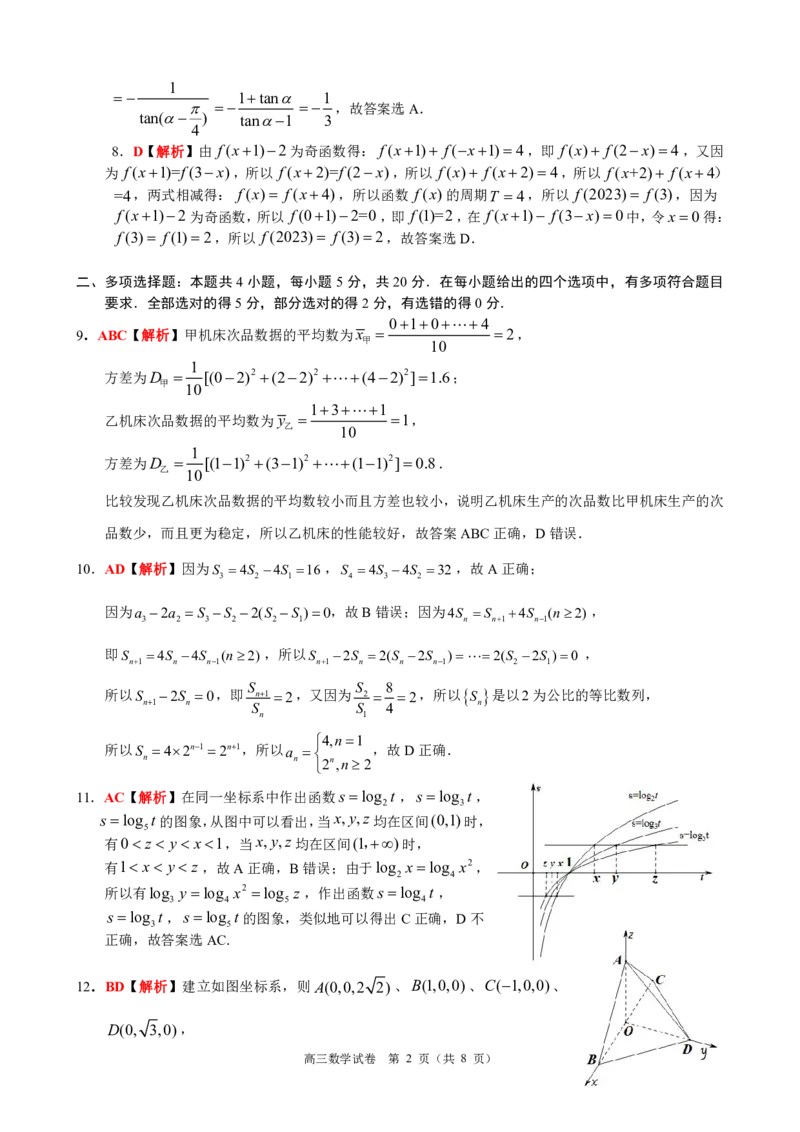11．AC【解析】在同一坐标系中作出函数s log t ，s log t， 2 3 s log t的图象，从图中可以看出，当x,y,z均在区间(0,1)时， 5 有0 z y x1，当x,y,z均在区间(1，)时， 有1 x y z ，故A正确，B错误；由于log xlog x2， 2 4 所以有log y log x2 log z ，作出函数s log t ， 3 4 5 4 s log t，s log t的图象，类似地可以得出C正确，D不 3 5 正确，故答案选AC. 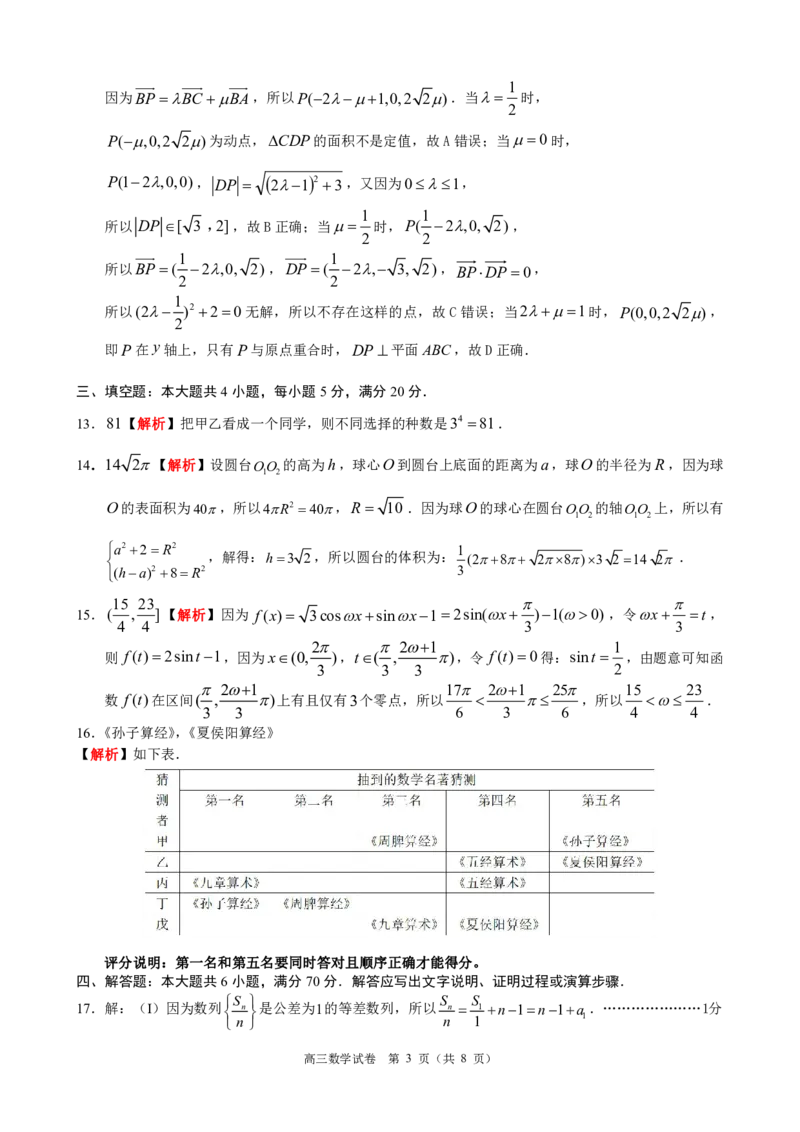12．BD【解析】建立如图坐标系，则A(0,0,2 2)、B(1,0,0)、C(1,0,0)、 D(0, 3,0)， 高三数学试卷 第 2 页（共 8 页） {#{QQABCYCEogCgAAJAAAgCUwHCCECQkAGCAIoGAFAEsAABQBFABAA=}#}   1 因为BP BCBA，所以P(21,0,2 2)．当 时， 2 P(,0,2 2)为动点，CDP的面积不是定值，故A错误；当0时， P(12,0,0)， DP   21 2 3，又因为01， 1 1 所以 DP [ 3 ， 2]，故B正确；当 时，P( 2,0, 2)， 2 2  1  1 所以BP ( 2,0, 2)，DP ( 2, 3, 2)， BPDP 0 ， 2 2 1 所以(2 )2 20无解，所以不存在这样的点，故C错误；当21时，P(0,0,2 2)， 2 即P在 y轴上，只有P与原点重合时，DP 平面ABC，故D正确． 三、填空题：本大题共4小题，每小题5分，满分20分． 13．81【解析】把甲乙看成一个同学，则不同选择的种数是34 81． 14．14 2【解析】设圆台OO 的高为h，球心O到圆台上底面的距离为a，球O的半径为R，因为球 1 2 O的表面积为40，所以4R2 40，R  10 ．因为球O的球心在圆台OO 的轴OO 上，所以有 1 2 1 2 a22 R2 1  ，解得：h3 2，所以圆台的体积为： (28 28)3 2 14 2 ． (ha)2 8R2 3 15 23   15．( , ]【解析】因为 f(x) 3cosxsinx12sin(x )1(0)，令x t， 4 4 3 3 2  21 1 则 f(t)2sint1，因为x(0, )，t( , )，令 f(t)0得：sint  ，由题意可知函 3 3 3 2  21 17 21 25 15 23 数 f(t)在区间( , )上有且仅有3个零点，所以   ，所以  ． 3 3 6 3 6 4 4 16．《孙子算经》，《夏侯阳算经》 【解析】如下表． 评分说明：第一名和第五名要同时答对且顺序正确才能得分。 四、解答题：本大题共6小题，满分70分．解答应写出文字说明、证明过程或演算步骤． S  S S 17．解：（I）因为数列  n 是公差为1的等差数列，所以 n  1 n1n1a ．…………………1分  n  n 1 1 高三数学试卷 第 3 页（共 8 页） {#{QQABCYCEogCgAAJAAAgCUwHCCECQkAGCAIoGAFAEsAABQBFABAA=}#}从而可得S n2 (a 1)n．………………………………………………………………………………2分 n 1 当n2时，a S S a 2(n1)．………………………………………………………………3分 n n n1 1 即可得a a 2，所以数列{a }是公差为2的等差数列；…………………………………………4分 n n1 n （II）根据第（1）问数列{a }是公差为2的等差数列可得S 3a 323a 69，………………5分 n 3 1 1 从而可得a 1．……………………………………………………………………………………………6分 1 所以数列{a }的通项公式a 2n1．……………………………………………………………………7分 n n 1 1 1 1 1  所以      ………………………………………………………8分 a a (2n1)(2n1) 22n1 2n1 n n1 11 1 1 1 1 1  1 1 从而可得T          ………………………………………9分 n 21 3 3 5 2n1 2n1 2 4n 2 1 所以T  成立．…………………………………………………………………………………………10分 n 2 18．解：（I）对函数 f(x)求导可得 f(x)ex a ．……………………………………………………1分 当a0时， f(x)0恒成立，可得函数 f(x)的单调递增区间为R，无单调递减区间；………3分 当a 0时，令 f(x)0，可得x(,lna)，可得函数 f(x)的单调递减区间为(,lna)； 令 f(x)0，可得x(lna,)，可得函数 f(x)的单调递增区间为(lna,)；………………5分 ex （II）法一：当x(1,)时， f(x)0恒成立等价于a ……………………………………6分 x1 ex exx 令g(x) ，则g(x) ……………………………………………………………………8分 x1 (x1)2 令g(x)0，可得x(1,0)，即有g(x)在(1,0)上单调递减；令g(x)0，可得x(0,)， 即有g(x)在(0,)上单调递增．………………………………………………………………………10分 从而可得函数g(x)的最小值为g(0)1. ……………………………………………………………11分 综上即可得a的取值范围是(,1]．…………………………………………………………………12分 法二：由（I）知，当a0时，函数 f(x)在(1,)上单调递增， 所以 f(x) f(1)e1 0满足题意，…………………………………………………………………7分 高三数学试卷 第 4 页（共 8 页） {#{QQABCYCEogCgAAJAAAgCUwHCCECQkAGCAIoGAFAEsAABQBFABAA=}#}当0ae1时，lna1，所以函数 f(x)的在(1,)上单调递增， 所以 f(x) f(1)e1 0满足题意，…………………………………………………………………9分 当a e1时，lna 1，函数 f(x)的在(1,lna)上单调递减，在(lna,)上单调递增， 所以[f(x)]  f(lna)aa(lna1)alna， min 因为 f(x)0，所以[f(x)] 0，即alna0，解得：e1 a1，………………………11分 min 综上，实数a的取值范围是(,1]．…………………………………………………………………12分 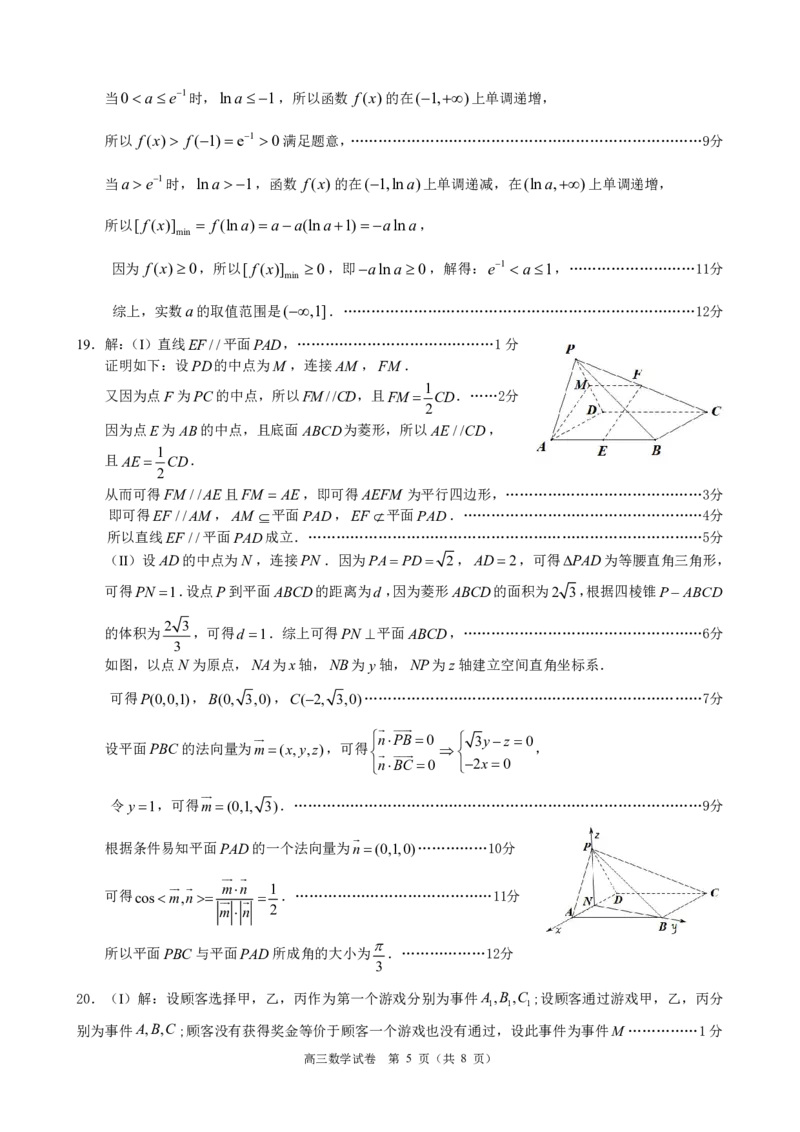19．解：（I）直线EF//平面PAD，……………………………………1分 证明如下：设PD的中点为M ，连接AM ，FM． 1 又因为点F 为PC的中点，所以FM//CD，且FM  CD．……2分 2 因为点E为AB的中点，且底面ABCD为菱形，所以AE//CD， 1 且AE CD． 2 从而可得FM //AE且FM  AE，即可得AEFM 为平行四边形，……………………………………3分 即可得EF//AM，AM 平面PAD，EF 平面PAD．……………………………………………4分 所以直线EF//平面PAD成立．…………………………………………………………………………5分 （II）设AD的中点为N ，连接PN．因为PA PD 2，AD2，可得PAD为等腰直角三角形， 可得PN 1．设点P到平面ABCD的距离为d，因为菱形ABCD的面积为2 3，根据四棱锥PABCD 2 3 的体积为 ，可得d 1．综上可得PN 平面ABCD，……………………………………………6分 3 如图，以点N 为原点，NA为x轴，NB为y轴，NP为z轴建立空间直角坐标系． 可得P(0,0,1)，B(0, 3,0)，C(2, 3,0)………………………………………………………………7分     nPB0  3yz0 设平面PBC的法向量为m(x,y,z)，可得    ， nBC 0 2x0  令y1，可得m(0,1, 3)．……………………………………………………………………………9分  根据条件易知平面PAD的一个法向量为n(0,1,0)……………10分     mn 1 可得cosm,n    ．……………………………………11分 m  n 2  所以平面PBC与平面PAD所成角的大小为 ．………………12分 3 20．（I）解：设顾客选择甲，乙，丙作为第一个游戏分别为事件A,B,C ;设顾客通过游戏甲，乙，丙分 1 1 1 别为事件A,B,C;顾客没有获得奖金等价于顾客一个游戏也没有通过，设此事件为事件M ……………1分 高三数学试卷 第 5 页（共 8 页） {#{QQABCYCEogCgAAJAAAgCUwHCCECQkAGCAIoGAFAEsAABQBFABAA=}#}1 由已知得P(A) P(B) P(C ) ,P(A| A)0.8,P(B|B)0.6,P(C|C )0.4………………………2分 1 1 1 3 1 1 1 由全概率公式得： P(M)P(A)P(A|A)P(B)P(B|B)P(C )P(C|C )…………………………………………………3分 1 1 1 1 1 1 1 1 1  (10.8）+ (10.6） (10.4）0.4……………………………………………………………4分 3 3 3 （II）设王先生获得奖金总额为X .按甲乙丙的顺序进行， 则X 的可能取值有0,100,300,600………………………………………………………………………5分 PX 00.2，PX 1000.80.40.32…………………………………………………………6分 PX 3000.80.60.60.288，PX 6000.80.60.40.192.……………………………7分 概率分布表为： X 0 100 300 600 P 0.2 0.32 0.288 0.192 EX00.21000.323000.2886000.192233.6.…………………………………………9分 同理，李先生按C B A的顺序获得奖金金额的均值为187.2元.………………………………11分 综上可知甲顾客获得奖金的期望值较大．………………………………………………………………12分 （注：若先算李先生的奖金情况，可参照上面的评分标准类似给分） 21．（I）解：因为(sinAsinB)(sinAsinB) sinBsinC，由正弦定理得a2 b2bc…………………1分 由余弦定理得a2 b2c22bccosA,所以有bc2bcosA…………………………………………………2分 1 因为c2b，所以b2b2bcosA，即cosA= ………………………………………………………………3分 2  因为0A，所以A= ……………………………………………………………………………………4分 3 （II）（i）证明：由（I）知bc2bcosA，由正弦定理得sinBsinC2sinBcosA…………………5分 因为sinC=sin((AB))sin（AB)，所以sinBsin（AB)2sinBcosAsin（AB)………………6分 因为0B,0AB,所以B=(AB)或B(AB)（舍），所以A2B…………………………7分 （II）（ii）由（i）得A2B，所以cosAcosBcosC=cos2BcosBcos3B…………………………8分 =cosB+2cos2B1cos(B2B)4cos32cos2B4cosB1………………………………………………9分  1 因为A2B，所以0B ，令xcosB, f(x)4x32x24x1,x( ,1）……………………………10分 3 2 1 131 131 因为 f(x)4(3x2x1)，由 f(x)0得 x ，由 f(x)0得 x1，所以 f(x)在 2 6 6 1 131 131 （ ， ）上递增，在（ ，1）上递减………………………………………………………………11分 2 6 6 1 因为 f( ) f(1)=1，所以 f(x) f(1)1，所以cosAcosBcosC1…………………………………12分 2 22．解：（I）设点A，B的坐标为(x,y )，(x ,y )． 1 1 2 2 x2 y2 x2 y2 将其代入椭圆方程可得 1  1 1； 2  2 1；……………………………………………………1分 a2 b2 a2 b2 高三数学试卷 第 6 页（共 8 页） {#{QQABCYCEogCgAAJAAAgCUwHCCECQkAGCAIoGAFAEsAABQBFABAA=}#}x2 x2 y2  y2 1 (y y )(y  y ) 两式相减可得 1 2  1 2 0，整理可得  1 2 1 2 0．………………………2分 a2 b2 a2 (x x )(x x )b2 1 2 1 2 y y 其中 1 2 为直线AB的斜率， x x 1 2 y y 1 可利用点P(1,1)及点F (3,0)计算可得 1 2  ．…………………………………………………3分 2 x x 2 1 2 y  y 2y 1 1 其中 1 2  P 1，代入上式可得  0，即可得a2 2b2．………………………………4分 x x 2x a2 2b2 1 2 P 根据椭圆三个参数间的关系：c2 a2b2 b2 9，可得a2 18． x2 y2 综上可得椭圆C的方程为  1．…………………………………………………………………5分 18 9 （II）解法一：设直线l的方程为ykxk1，设点F 关于直线l的对称点为F ，从椭圆C的左焦点F 1 1 1 发射一束光线经过直线l进行反射后的反射光线必经过点F ． 1 现计算点F 的坐标，设过点F(3,0)且与直线l垂直的直线为l:xky3． 1 1 直线l与直线l的交点为T   k2k3 , 14k  ，从而可得点F 的坐标为   5k22k3 , 28k  ．……7分  k21 k21 1  k21 k21 为了保证经过椭圆反射后再回到点F，根据椭圆的光学性质可知上述反射光线会经过椭圆的右焦点 1 F (3,0)，综上可知点P(1,1)，F (3,0)，F 三点共线．………………………………………………8分 2 2 1 9 85 即可知k k ，即有k29k10，经计算可得k  ．…………………………………9分 PF2 F1 F2 2 9 85 符合条件的直线方程为y (x1)1．…………………………………………………………10分 2 9 85 当直线l为y (x1)1时，根据条件易知PF  17，PF  5．根据椭圆的定义经过点P的 1 2 2 反射光线及经过椭圆的后的反射光线的和为2aPF 6 2 5． 2 此时光线闭合三角形的周长为6 2 17 5．………………………………………………………11分 9 85 当直线l为y (x1)1时，根据条件易知PF  17，PF  5．根据椭圆的定义经过点P的 1 2 2 反射光线及经过椭圆的后的反射光线的和为2aPF 6 2 5． 2 此时“光线三角形”的周长为6 2 17 5．………………………………………………………12分 （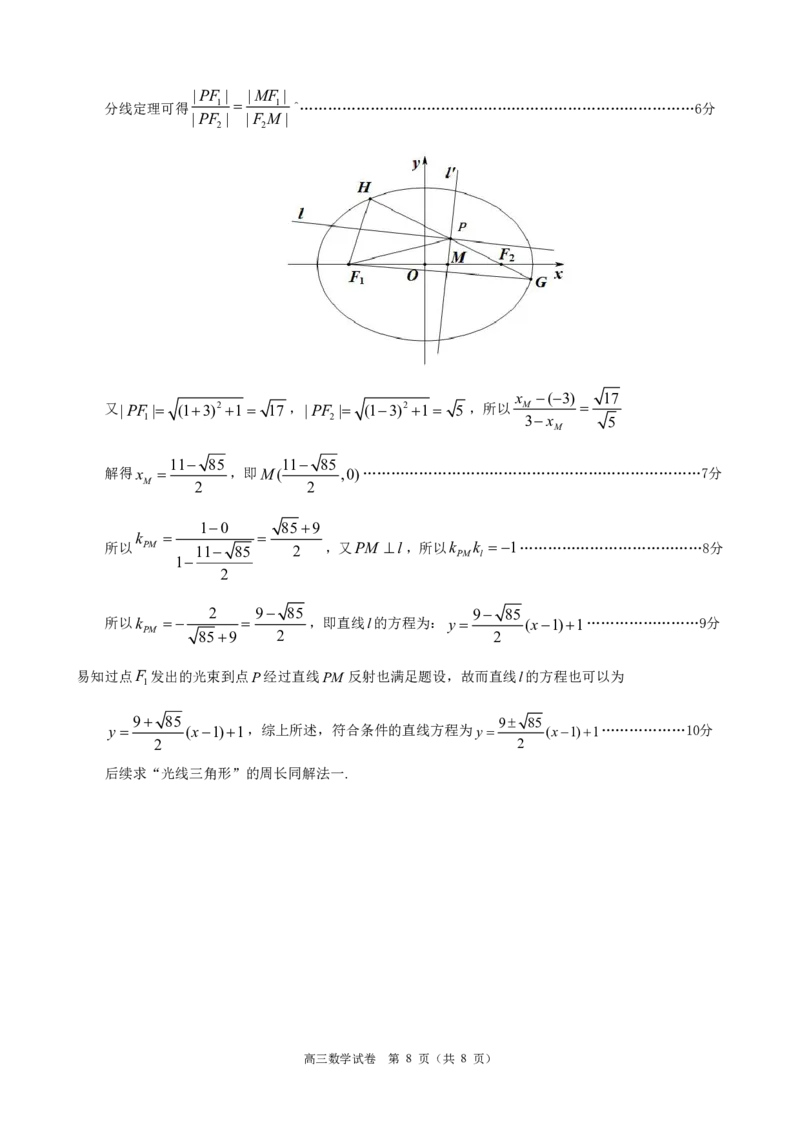II）解法二：如图，如果过点 F 的光线经过点 P 被直线 l 反射后经过点 F 交下半椭圆于点 G ，过设 1 1 过点P且与直线l垂直的直线为 l ，直线 l 与x轴交于点M ，由题意可知，FPM F PM ,由角平 1 2 高三数学试卷 第 7 页（共 8 页） {#{QQABCYCEogCgAAJAAAgCUwHCCECQkAGCAIoGAFAEsAABQBFABAA=}#}|PF | |MF | 分线定理可得 1  1 ^…………………………………………………………………………6分 |PF | |F M | 2 2 x (3) 17 又|PF | (13)21 17 ，|PF | (13)21 5 ，所以 M  1 2 3x 5 M 11 85 11 85 解得x  ，即M( ,0)………………………………………………………………7分 M 2 2 10 859 k   所以 PM 11 85 2 ，又PM l，所以k PM k l 1…………………………………8分 1 2 2 9 85 9 85 所以k   ，即直线l的方程为： y  (x1)1……………………9分 PM 859 2 2 易知过点F 发出的光束到点P经过直线PM 反射也满足题设，故而直线l的方程也可以为 1 9 85 9 85 y  (x1)1，综上所述，符合条件的直线方程为y (x1)1………………10分 2 2 后续求“光线三角形”的周长同解法一. 高三数学试卷 第 8 页（共 8 页） {#{QQABCYCEogCgAAJAAAgCUwHCCECQkAGCAIoGAFAEsAABQBFABAA=}#}