文档内容
专题 1.3 空间向量基本定理【八大题型】
【人教A版(2019)】
【题型1 空间向量基底的判断】..............................................................................................................................1
【题型2 用空间基底表示向量】..............................................................................................................................3
【题型3 由空间向量基本定理求参数】..................................................................................................................6
【题型4 正交分解】..................................................................................................................................................8
【题型5 利用空间向量基本定理证明平行、共线、共面问题】.......................................................................11
【题型6 利用空间向量基本定理求夹角】...........................................................................................................13
【题型7 利用空间向量基本定理证明垂直问题】...............................................................................................16
【题型8 利用空间向量基本定理求距离(长度)问题】.........................................................................................20
【知识点1 空间向量基本定理】
1.空间向量基本定理
如果三个向量a,b,c不共面,那么对任意一个空间向量p,存在唯一的有序实数组(x,y,z),使得p
=xa+yb+zc.
我们把{a,b,c}叫做空间的一个基底,a,b,c都叫做基向量.
2.用基底表示向量的步骤:
(1)定基底:根据已知条件,确定三个不共面的向量构成空间的一个基底.
(2)找目标:用确定的基底(或已知基底)表示目标向量,需要根据三角形法则及平行四边形法则,结
合
相等向量的代换、向量的运算进行变形、化简,最后求出结果.
(3)下结论:利用空间的一个基底{ , , }可以表示出空间所有向量.表示要彻底,结果中只能含
有 , , ,不能含有其他形式的向量.
【题型1 空间向量基底的判断】
【例1】(2023春·河南开封·高二统考期末)若{⃗a,⃗b,⃗c}构成空间的一个基底,则下列向量可以构成空间基
底的是( )
学科网(北京)股份有限公司A.⃗a+⃗b,⃗a−⃗b,⃗a B.⃗a+⃗b,⃗a−⃗b,⃗b C.⃗a+⃗b,⃗a−⃗b,⃗b+⃗c D.⃗a+⃗b,⃗a+⃗b+⃗c,⃗c
【解题思路】根据空间基底的概念逐项判断,可得出合适的选项.
1
【解答过程】对于A,⃗a= [(⃗a+⃗b)+(⃗a−⃗b)] ,因此向量⃗a+⃗b,⃗a−⃗b,⃗a共面,故不能构成基底,故A错误;
2
1
对于B,⃗b= [(⃗a+⃗b)−(⃗a−⃗b)] ,因此向量⃗a+⃗b,⃗a−⃗b,⃗b共面,故不能构成基底,故B错误;
2
对于C,假设向量⃗a+⃗b,⃗a−⃗b,⃗b+⃗c共面,则⃗b+⃗c=λ(⃗a+⃗b)+μ(⃗a−⃗b),
即⃗c=(λ+μ)⃗a+(λ−μ−1)⃗b,这与题设矛盾,假设不成立,可以构成基底,故C正确;
对于D,(⃗a+⃗b)+⃗c=⃗a+⃗b+⃗c,因此向量⃗a+⃗b,⃗a+⃗b+⃗c,⃗c共面,故不能构成基底,故D错误;
故选:C.
【变式1-1】(2023春·湖南·高一校联考期末)已知{⃗a,⃗b,⃗c}是空间的一个基底,若⃗p=⃗a+⃗b,⃗q=⃗a+⃗c,则
下列与⃗p,⃗q构成一组空间基底的是( )
A.r⃗=2⃗b−3⃗c B.r⃗=⃗a−⃗b+2⃗c
C.r⃗=⃗a+2⃗b−⃗c D.r⃗=2⃗a+⃗b+⃗c
【解题思路】根据构成空间基底的条件对选项进行分析,从而确定正确答案.
【解答过程】A.设r⃗=x⃗p+ y⃗q,所以2⃗b−3⃗c=x(⃗a+⃗b)+ y(⃗a+⃗c),
整理得,2⃗b−3⃗c=(x+ y)⃗a+x⃗b+ y⃗c,
因为{⃗a,⃗b,⃗c}是空间的一个基底,所以¿,无解.
所以⃗p,⃗q与r⃗构成一个基底.
B.因为r⃗=⃗a−⃗b+2⃗c,所以r⃗=2⃗q−⃗p,所以排除B;
C.因为r⃗=⃗a+2⃗b−⃗c,所以r⃗=2⃗p−⃗q,所以排除C;
D.设r⃗=x⃗p+ y⃗q,所以2⃗a+⃗b+⃗c=x(⃗a+⃗b)+ y(⃗a+⃗c),
整理得,2⃗a+⃗b+⃗c=(x+ y)⃗a+x⃗b+ y⃗c,
因为{⃗a,⃗b,⃗c}是空间的一个基底,所以¿,所以¿,
所以⃗p,⃗q与r⃗不构成一个基底,排除D.
学科网(北京)股份有限公司故选:A.
【变式1-2】(2023春·内蒙古兴安盟·高二校考阶段练习)若⃗a,⃗b,⃗c构成空间的一个基底,则下列向量
能构成空间的一个基底的是( )
A.⃗a+⃗b,⃗a−⃗c,⃗b B.⃗c,⃗b+⃗c,⃗b−⃗c
C.⃗b+⃗c,⃗a+⃗b+⃗c,⃗a D.⃗a,⃗a+⃗b,⃗a−⃗b
【解题思路】根据空间向量共面定理可知BCD选项中的向量共面,无法作为一组基底;假设A中向量共
面,可知不存在满足条件的实数λ,μ,由此知假设错误,则A中向量可以作为基底.
【解答过程】对于A,假设⃗a+⃗b,⃗a−⃗c,⃗b共面,则可设⃗a+⃗b=λ(⃗a−⃗c)+μ⃗b(λ,μ∈R)
∴¿,方程组无解,⃗a+⃗b,⃗a−⃗c,⃗b不共面,可以作为空间一组基底,A正确;
→ 1(→ →) 1(→ →)
对于B,c= b+c − b−c ,∴⃗c,⃗b+⃗c,⃗b−⃗c共面,不能作为空间一组基底,B错误;
2 2
对于C, → b+ → c= (→ a+ → b+ → c ) − → a ,∴⃗b+⃗c,⃗a+⃗b+⃗c,⃗a共面,不能作为空间一组基底,C错误;
1 1
对于D,∵⃗a= (⃗a+⃗b)+ (⃗a−⃗b),∴⃗a,⃗a+⃗b,⃗a−⃗b共面,不能作为空间一组基底,D错误.
2 2
故选:A.
【变式1-3】(2023秋·云南大理·高二统考期末)若{⃗e ,⃗e ,⃗e }是空间的一个基底,且向量
1 2 3
{⃗OA=⃗e +⃗e +⃗e ,⃗OB=⃗e −2⃗e +2⃗e ,⃗OC=⃗ke +3⃗e +⃗2e }不能构成空间的一个基底,则k=( )
1 2 3 1 2 3 1 2 3
8 5 1 9
A. B. C.− D.
3 2 4 4
【解题思路】由题意可知,向量⃗OA、⃗OB、⃗OC共面,则存在实数x、y使得⃗OC=x⃗OA+ y⃗OB,根据空
间向量的基本定理可得出关于x、y、k的方程组,即可解得k的值.
【解答过程】因为向量⃗OA=⃗e +⃗e +⃗e ,⃗OB=⃗e −2⃗e +2⃗e ,⃗OC=k⃗e +3⃗e +2⃗e 不能构成空间的一个
1 2 3 1 2 3 1 2 3
基底,
所以⃗OA、⃗OB、⃗OC共面,故存在实数x、y使得⃗OC=x⃗OA+ y⃗OB,
即k⃗e +3⃗e +2⃗e =x(⃗e +⃗e +⃗e )+ y(⃗e −2⃗e +2⃗e )=(x+ y)⃗e +(x−2y)⃗e +(x+2y)⃗e ,
1 2 3 1 2 3 1 2 3 1 2 3
因为{⃗e ,⃗e ,⃗e }是空间的一个基底,则¿,解得¿.
1 2 3
学科网(北京)股份有限公司故选:D.
【题型2 用空间基底表示向量】
【例2】(2023·全国·高二专题练习)在四面体O−ABC中,⃗PA=2⃗OP,Q是BC的中点,且M为PQ的
中点,若⃗OA=⃗a,⃗OB=⃗b,⃗OC=⃗c,则⃗OM=( )
1 1 1 1 1 1
A. ⃗a+ ⃗b+ ⃗c B. ⃗a+ ⃗b+ ⃗c
6 4 4 6 2 2
1 1 1 1 1 1
C. ⃗a+ ⃗b+ ⃗c D. ⃗a+ ⃗b+ ⃗c
3 2 2 3 4 4
【解题思路】利用基底⃗a,⃗b,⃗c表示⃗OP,⃗OQ,再利用向量线性运算求解即可.
1
【解答过程】因为 2O → P=P → A ,所以⃗OP= ⃗OA,
3
1
因为Q是BC的中点,所以⃗OQ= (⃗OB+⃗OC),
2
1 1 1 1 1 1 1 1
因为M为PQ的中点,所以⃗OM= (⃗OP+⃗OQ) = ⃗OP+ ⃗OQ = ⃗OA+ (⃗OB+⃗OC) = ⃗a+ ⃗b+ ⃗c,
2 2 2 6 4 6 4 4
故选:A.
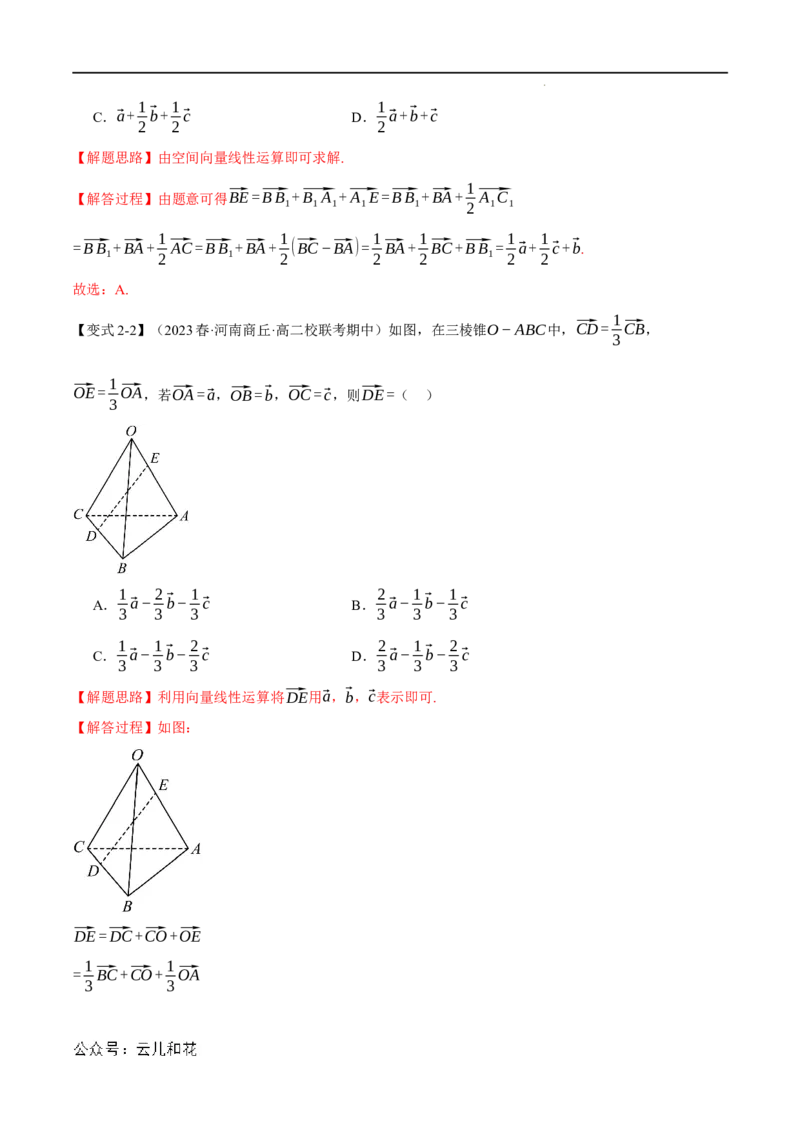
【变式2-1】(2023春·福建龙岩·高二校联考期中)如图,在直三棱柱ABC−A B C 中,E为棱A C 的
1 1 1 1 1
中点.设⃗BA=⃗a,⃗BB =⃗b,⃗BC=⃗c,则⃗BE=( )
1
1 1 1 1
A. ⃗a+⃗b+ ⃗c B. ⃗a+ ⃗b+⃗c
2 2 2 2
学科网(北京)股份有限公司1 1 1
C.⃗a+ ⃗b+ ⃗c D. ⃗a+⃗b+⃗c
2 2 2
【解题思路】由空间向量线性运算即可求解.
1
【解答过程】由题意可得⃗BE=⃗BB +⃗B A +⃗A E=⃗BB +⃗BA+ ⃗A C
1 1 1 1 1 2 1 1
1 1 1 1 1 1
=⃗BB +⃗BA+ ⃗AC=⃗BB +⃗BA+ (⃗BC−⃗BA)= ⃗BA+ ⃗BC+⃗BB = ⃗a+ ⃗c+⃗b.
1 2 1 2 2 2 1 2 2
故选:A.
1
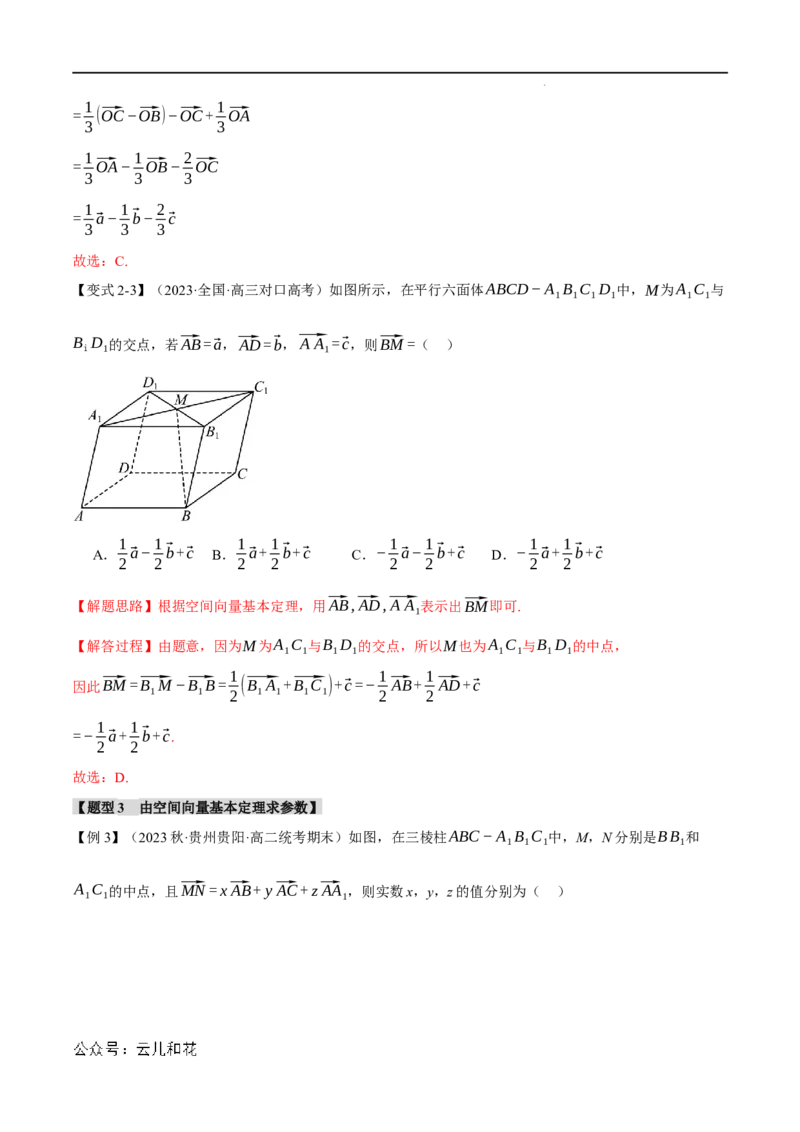
【变式2-2】(2023春·河南商丘·高二校联考期中)如图,在三棱锥O−ABC中,⃗CD= ⃗CB,
3
1
⃗OE= ⃗OA,若⃗OA=⃗a,⃗OB=⃗b,⃗OC=⃗c,则⃗DE=( )
3
1 2 1 2 1 1
A. ⃗a− ⃗b− ⃗c B. ⃗a− ⃗b− ⃗c
3 3 3 3 3 3
1 1 2 2 1 2
C. ⃗a− ⃗b− ⃗c D. ⃗a− ⃗b− ⃗c
3 3 3 3 3 3
【解题思路】利用向量线性运算将⃗DE用⃗a,⃗b,⃗c表示即可.
【解答过程】如图:
⃗DE=⃗DC+⃗CO+⃗OE
1 1
= ⃗BC+⃗CO+ ⃗OA
3 3
学科网(北京)股份有限公司1 1
= (⃗OC−⃗OB)−⃗OC+ ⃗OA
3 3
1 1 2
= ⃗OA− ⃗OB− ⃗OC
3 3 3
1 1 2
= ⃗a− ⃗b− ⃗c
3 3 3
故选:C.
【变式2-3】(2023·全国·高三对口高考)如图所示,在平行六面体ABCD−A B C D 中,M为A C 与
1 1 1 1 1 1
B D 的交点,若⃗AB=⃗a,⃗AD=⃗b,⃗A A =⃗c,则⃗BM=( )
i 1 1
1 1 1 1 1 1 1 1
A. ⃗a− ⃗b+⃗c B. ⃗a+ ⃗b+⃗c C.− ⃗a− ⃗b+⃗c D.− ⃗a+ ⃗b+⃗c
2 2 2 2 2 2 2 2
【解题思路】根据空间向量基本定理,用⃗AB,⃗AD,⃗A A 表示出⃗BM即可.
1
【解答过程】由题意,因为M为A C 与B D 的交点,所以M也为A C 与B D 的中点,
1 1 1 1 1 1 1 1
1 1 1
因此⃗BM=⃗B M−⃗B B= (⃗B A +⃗B C )+⃗c=− ⃗AB+ ⃗AD+⃗c
1 1 2 1 1 1 1 2 2
1 1
=− ⃗a+ ⃗b+⃗c.
2 2
故选:D.
【题型3 由空间向量基本定理求参数】
【例3】(2023秋·贵州贵阳·高二统考期末)如图,在三棱柱ABC−A B C 中,M,N分别是BB 和
1 1 1 1
A C 的中点,且⃗MN=x⃗AB+ y⃗AC+z⃗AA ,则实数x,y,z的值分别为( )
1 1 1
学科网(北京)股份有限公司1 1 1 1 1 1 1 1
A.−1, , B.−1, ,− C.−1,− ,− D.1,− ,
2 2 2 2 2 2 2 2
【解题思路】根据题意用空间基底向量表示向量,结合空间向量的线性运算求解.
【解答过程】由题意可得:
1 1 1 1
⃗MN=⃗MB +⃗B C +⃗C N= ⃗A A +(⃗AC−⃗AB)− ⃗AC=−⃗AB+ ⃗AC+ ⃗A A ,
1 1 1 1 2 1 2 2 2 1
1 1
故x=−1,y= ,z=
.
2 2
故选:A.
【变式3-1】(2023秋·高二课时练习)已知BA,BC,BB 为三条不共面的线段,若
1
⃗AC =x⃗AB+2y⃗BC+3z⃗C C,那么x+ y+z=( )
1 1
7 5 11
A.1 B. C. D.
6 6 6
【解题思路】直接利用共面向量的基本定理求出结果.
【解答过程】根据向量加法法则可得:⃗AC =⃗AB+⃗BC+⃗CC ,
1 1
即⃗AC =⃗AB+⃗BC−⃗C C,
1 1
因为⃗AC =x⃗AB+2y⃗BC+3z⃗C C,
1 1
所以x=1,2y=1,3z=−1,
1 1 1 1 7
所以x=1,y= ,z=− ,所以x+ y+z=1+ − = .
2 3 2 3 6
故选:B.
【变式3-2】(2023春·四川绵阳·高二校考阶段练习)已知四面体O-ABC,G 是 ABC的重心,G是OG
1 1
上一点,且OG=3GG ,若⃗OG=x⃗OA+ y⃗OB+z⃗OC,则(x,y,z)为( ) △
1
(1 1 1) (3 3 3)
A. , , B. , ,
4 4 4 4 4 4
学科网(北京)股份有限公司(1 1 1) (2 2 2)
C. , , D. , ,
3 3 3 3 3 3
【解题思路】连接AG 并延长,交BC于点E,利用向量加减、数乘几何意义用⃗OA,⃗OB,⃗OC表示出⃗OG,
1
即可得答案.
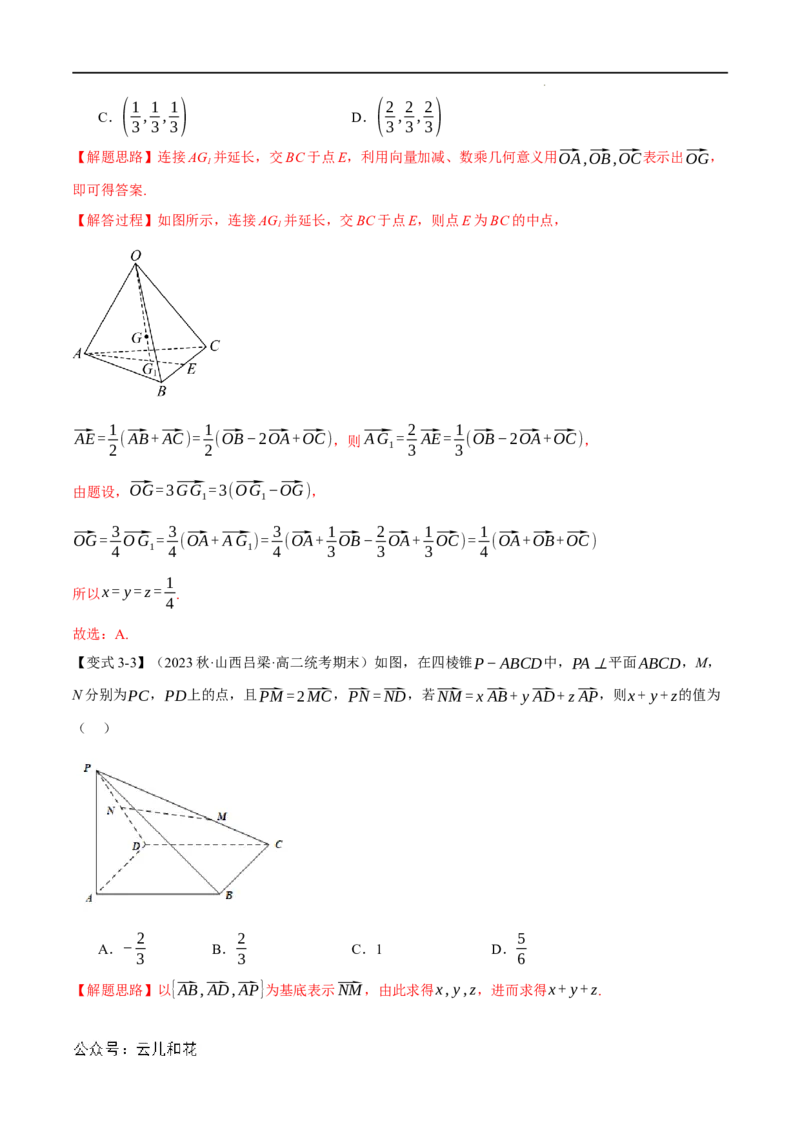
【解答过程】如图所示,连接AG 并延长,交BC于点E,则点E为BC的中点,
1
1 1 2 1
⃗AE= (⃗AB+⃗AC)= (⃗OB−2⃗OA+⃗OC),则⃗AG = ⃗AE= (⃗OB−2⃗OA+⃗OC),
2 2 1 3 3
由题设,⃗OG=3⃗GG =3(⃗OG −⃗OG),
1 1
3 3 3 1 2 1 1
⃗OG= ⃗OG = (⃗OA+⃗AG )= (⃗OA+ ⃗OB− ⃗OA+ ⃗OC)= (⃗OA+⃗OB+⃗OC)
4 1 4 1 4 3 3 3 4
1
所以x= y=z=
.
4
故选:A.
【变式3-3】(2023秋·山西吕梁·高二统考期末)如图,在四棱锥P−ABCD中,PA⊥平面ABCD,M,
N分别为PC,PD上的点,且⃑PM=2⃑MC,⃑PN=⃑ND,若⃑NM=x⃑AB+ y⃑AD+z⃑AP,则x+ y+z的值为
( )
2 2 5
A.− B. C.1 D.
3 3 6
【解题思路】以{⃑AB,⃑AD,⃑AP}为基底表示⃑NM,由此求得x,y,z,进而求得x+ y+z.
学科网(北京)股份有限公司1
【解答过程】⃑NM=⃑AM−⃑AN=⃑AC+⃑CM− (⃑AD+⃑AP)
2
1 1 1
=⃑AB+⃑AD+ ⃑CP− ⃑AD− ⃑AP
3 2 2
1 1 1
=⃑AB+ ⃑AD+ (⃑AP−⃑AC)− ⃑AP
2 3 2
1 1 1 1
=⃑AB+ ⃑AD+ ⃑AP− ⃑AC− ⃑AP
2 3 3 2
1 1 1
=⃑AB+ ⃑AD− (⃑AB+⃑AD)− ⃑AP
2 3 6
2 1 1
= ⃑AB+ ⃑AD− ⃑AP,
3 6 6
2 1 1 2
所以x= ,y= ,z=− ,x+ y+z=
.
3 6 6 3
故选:B.
【知识点2 空间向量的正交分解】
1.空间向量的正交分解
(1)单位正交基底
如果空间的一个基底中的三个基向量两两垂直,且长度都是1,那么这个基底叫做单位正交基底 ,常
用{i,j,k}表示.
(2)向量的正交分解
由空间向量基本定理可知,对空间任一向量a,均可以分解为三个向量xi,yj,zk使得a=xi+yj+zk.
像这样把一个空间向量分解为三个两两垂直的向量,叫做把空间向量进行正交分解.
【题型4 正交分解】
【例4】(2022·全国·高一假期作业)设{i⃗,⃗j,⃗k}是单位正交基底,已知向量⃗p在基底{⃗a,⃗b,⃗c}下的坐标为
(8,6,4),其中⃗a=i⃗+⃗j,⃗b=⃗j+⃗k,⃗c=⃗k+i⃗,则向量⃗p在基底{i⃗,⃗j,⃗k}下的坐标是( )
A.(10,12,14) B.(12,14,10) C.(14,12,10) D.(4,3,2)
【解题思路】由题设得⃗p=8⃗a+6⃗b+4⃗c,结合已知条件求⃗p关于i⃗,⃗j,⃗k的线性表达式,即可知在基底
{i⃗,⃗j,⃗k}下的坐标.
【解答过程】由题设知:⃗p=8⃗a+6⃗b+4⃗c,而⃗a=i⃗+⃗j,⃗b=⃗j+⃗k,⃗c=⃗k+i⃗,
∴⃗p=8(i⃗+⃗j)+6(⃗j+⃗k)+4(⃗k+i⃗)=12i⃗+14⃗j+10⃗k,
学科网(北京)股份有限公司∴⃗p在基底{i⃗,⃗j,⃗k}下的坐标是(12,14,10).
故选:B.
【变式4-1】(2023春·高二课时练习)已知{⃗a,⃗b,⃗c}是空间的一个单位正交基底,向量⃗p=⃗a+2⃗b+3⃗c,
{⃗a+⃗b,⃗a−⃗b,⃗c}是空间的另一个基底,向量⃗p在基底{⃗a+⃗b,⃗a−⃗b,⃗c}下的坐标为( )
(3 1 ) ( 3 1 ) (1 3 ) ( 1 3 )
A. ,− ,3 B. − , ,3 C. ,− ,3 D. − , ,3
2 2 2 2 2 2 2 2
【解题思路】设p=x(⃗a+⃗b)+ y(⃗a−⃗b)+z⃗c,根据空间向量基本定理建立关于x,y,z的方程,解之即可得
解.
【解答过程】解:设p=x(⃗a+⃗b)+ y(⃗a−⃗b)+z⃗c
=(x+ y)⃗a+(x−y)⃗b+z⃗c=⃗a+2⃗b+3⃗c,
所以¿,解得¿,
(3 1 )
所以向量⃗p在基底{⃗a+⃗b,⃗a−⃗b,⃗c}下的坐标为 ,− ,3 .
2 2
故选:A.
【变式4-2】(2023秋·河北邯郸·高二统考期末)已知SA⊥平面ABC,AB⊥AC,SA=AB=1,
BC=√5,则空间的一个单位正交基底可以为( )
{ 1 }
A. ⃗AB, ⃗AC,⃗AS B.{⃗AB,⃗AC,⃗AS}
2
{ 1 1 } { √5 }
C. ⃗AB, ⃗AC, ⃗AS D. ⃗AS,⃗AB, ⃗BC
2 2 5
【解题思路】根据正交基地的定义可知,三个向量两两互相垂直,且模长为1.
【解答过程】因为SA⊥平面ABC,AB、AC都在面ABC内,
所以SA⊥AB,SA⊥AC.
因为AB⊥AC,AB=1,BC=√5,所以AC=2,又SA=1,
{ 1 }
所以空间的一个单位正交基底可以为 ⃗AB, ⃗AC,⃗AS .
2
故选:A.
学科网(北京)股份有限公司【变式4-3】(2022秋·山西大同·高二校考阶段练习)已知向量⃗a,⃗b,⃗c是空间的一个单位正交基底,向量
⃗a+⃗b,⃗a−⃗b,⃗a+⃗c是空间的另一个基底,若向量⃗p在基底⃗a,⃗b,⃗c下的坐标为(2,3,4),则⃗p在⃗a+⃗b,⃗a−⃗b,
⃗a+⃗c下的坐标为( )
( 1 5 ) (5 1 )
A. − , ,4 B. , ,4
2 2 2 2
(1 5 ) (5 1 )
C. ,− ,4 D. ,− ,4
2 2 2 2
【解题思路】可设向量⃗a=(1,0,0),⃗b=(0,1,0),⃗c=(0,0,1),由此把向量⃗a+⃗b,⃗a−⃗b,⃗a+⃗c分别用坐标
表示,列方程组解出x,y,z,即可得到⃗p的坐标.
【解答过程】不妨设向量⃗a=(1,0,0),⃗b=(0,1,0),⃗c=(0,0,1);
则向量⃑a+⃗b=(1,1,0),⃑a−⃗b=(1,−1,0),⃗a+⃗c=(1,0,1).
设⃗p=x(⃑a+⃑b)+ y(⃑a−⃗b)+z(⃗a+⃗c),
即(2,3,4)=x(1,1,0)+ y(1,−1,0)+z(1,0,1),
∴¿解得¿
(1 5 )
即⃗p在⃗a+⃗b,⃗a−⃗b,⃗a+⃗c下的坐标为 ,− ,4 .
2 2
故选:C.
【知识点3 用空间向量基本定理解决相关的几何问题】
1.证明平行、共线、共面问题
(1)对于空间任意两个向量a,b(b≠0),a∥b的充要条件是存在实数λ,使a=λb.
(2)如果两个向量a,b不共线,那么向量p与向量a,b共面的充要条件是存在唯一的有序实数对(x,
y),使p=xa+yb.
2.求夹角、证明垂直问题
(1)θ为a,b的夹角,则cos θ=.
(2)若a,b是非零向量,则a⊥b⇔a·b=0.
3.求距离(长度)问题
=( = ).
4.利用空间向量基本定理解决几何问题的思路:
(1)平行和点共线都可以转化为向量共线问题;点线共面可以转化为向量共面问题;
(2)几何中的求夹角、证明垂直都可以转化为向量的夹角问题,解题中要注意角的范围;
(3)几何中求距离(长度)都可以转化为向量的模,用向量的数量积可以求得.
【注】用已知向量表示某一向量的三个关键点:
学科网(北京)股份有限公司(1)用已知向量来表示某一向量,一定要结合图形,以图形为指导是解题的关键.
(2)要正确理解向量加法、减法与数乘运算的几何意义,如首尾相接的若干向量之和,等于由起始向量
的始点指向末尾向量的终点的向量.
(3)在立体几何中三角形法则、平行四边形法则仍然成立.
【题型5 利用空间向量基本定理证明平行、共线、共面问题】
【例5】(2022·高二课时练习)A是△BCD所在平面外一点,G是△BCD的重心,M、E分别是BD、AG
2
的中点,点F在线段AM上,|AF|= |AM|,判断三点C、E、F是否共线.
5
【解题思路】利用空间向量的基本定理和共线向量定理求解.
【解答过程】解:设⃑AD=⃗a,⃑AC=⃗b,⃑AB=⃗c,
1 1 2 1
⃑CE= (⃑CG−⃗b)= ⋅ ⃑CM− ⃗b,
2 2 3 2
1 1 1[1 ] 1
= (⃑AM−⃗b)− ⃗b= (⃗a+⃗c)−⃗b − ⃗b,
3 2 3 2 2
1 5 1
= ⃗a− ⃗b+ ⃗c,
6 6 6
2 1 1 1
⃑CF=⃑AF−⃗b= ⃑AM−⃗b= (⃗a+⃗c)−⃗b= ⃗a−⃗b+ ⃗c,
5 5 5 5
5
因为⃑CE= ⃑CF,
6
所以⃑CE∥⃑CF,
又因为⃑CE、⃑CF有公共点C,
所以C、E、F三点共线.
【变式5-1】(2023春·高二课时练习)如图,正方体ABCD−A B C D 中,O为A C上一点,且
1 1 1 1 1
2
⃗A O= ⃗A C,BD与AC交于点M.求证:C ,O,M三点共线.
1 3 1 1
学科网(北京)股份有限公司【解题思路】取空间的基底,利用空间向量基本定理探求⃗MC ,⃗MO的关系,即可推理作答.
1
【解答过程】在正方体ABCD−A B C D 中,令⃗AB=⃗a,⃗AD=⃗b,⃗A A =⃗c,
1 1 1 1 1
2
⃗A O= ⃗A C,BD与AC交于点M,即点M是AC的中点,
1 3 1
1 1 1 1 1 1
于是⃗MO=⃗MC+⃗CO= ⃗AC+ ⃗C A = ⃗AC+ (⃗A A −⃗AC)= ⃗AC+ ⃗A A
2 3 1 2 3 1 6 3 1
1 1 1 1 1
= (⃗AB+⃗AD)+ ⃗A A = ⃗a+ ⃗b+ ⃗c,
6 3 1 6 6 3
1 1 1 1
⃗MC =⃗MC+⃗CC = ⃗AC+⃗A A = (⃗AB+⃗AD)+⃗A A = ⃗a+ ⃗b+⃗c,
1 1 2 1 2 1 2 2
因此⃗MC =3⃗MO,即⃗MC //⃗MO,而直线MC 与直线MO有公共点M,
1 1 1
所以C ,O,M三点共线.
1
【变式5-2】(2022秋·广东中山·高二校考阶段练习)在空间四边形ABCD中,H,G分别是AD,CD的中
CF AE 1
点,E,F分别边AB,BC上的点,且 = = ,⃗CA=⃗a,⃗CB=⃗b,⃗DC=⃗c
FB EB 3
(1)求⃗FH(用向量⃗a,⃗b,⃗c表示);
(2)求证:点E,F,G,H四点共面.
【解题思路】(1)根据向量的线性运算结合空间向量基本定理运算求解;(2)根据中位线和平行线的性
质,结合平行线的传递性证明EF∥HG,即可证结论.
【解答过程】(1)
1 1 1 1 1 1 1
∵⃗FH=⃗FC+⃗CD+⃗DH=− ⃗CB+⃗CD+ ⃗DA=− ⃗CB−⃗DC+ (⃗DC+⃗CA)= ⃗CA− ⃗CB− ⃗DC
4 2 4 2 2 4 2
1 1 1
∴⃗FH= ⃗a− ⃗b− ⃗c
2 4 2
(2)
学科网(北京)股份有限公司连接HG,EF
∵H,G分别是AD,CD的中点,∴HG∥AC.
CF AE 1
又∵ = = ,∴EF∥AC,
FB EB 3
∴EF∥HG,则E,F,G,H四点共面.
【变式5-3】(2023秋·高二课时练习)已知A,B,C三点不共线,对平面ABC外的任一点O,若点M满
1
足⃑OM= (⃑OA+⃑OB+⃑OC).
3
(1)判断⃑MA,⃑MB,⃑MC三个向量是否共面;
(2)判断点M是否在平面ABC内.
【解题思路】(1)根据空间向量的线性运算,结合平面向量基本定理证明即可;
(2)根据(1)结合平面向量的基本定理判断即可.
【解答过程】(1)由题知⃑OA+⃑OB+⃑OC=3⃑OM,
∴⃑OA−⃑OM=⃑OM−⃑OB+⃑OM−⃑OC,
即⃑MA=⃑BM+⃑CM=−⃑MB−⃑MC,
∴⃑MA,⃑MB,⃑MC共面.
(2)由(1)知,⃑MA,⃑MB,⃑MC共面且基线过同一点M,
∴M,A,B,C四点共面,从而点M在平面ABC内.
【题型6 利用空间向量基本定理求夹角】
【例6】(2022秋·湖北省直辖县级单位·高二校考期中)如图,正四面体ABCD(所有棱长均相等)的棱
长为1,E,F,G,H分别是正四面体ABCD中各棱的中点,设⃗AB=⃗a,⃗AC=⃗b,⃗AD=⃗c.
学科网(北京)股份有限公司(1)用⃗AB=⃗a,⃗AC=⃗b,⃗AD=⃗c表示⃗EF,并求⃗EF的长;
(2)求⃗EF与⃗GH的夹角.
【解题思路】(1)根据给定条件,利用空间向量基底表示⃗EF,再利用向量数量积的运算律求出⃗EF的长
作答.
(2)用空间向量基底表示⃗GH,再求出⃗EF与⃗GH的数量积即可作答.
【解答过程】(1)因E,F分别为棱BC,AD的中点,而⃗AB=⃗a,⃗AC=⃗b,⃗AD=⃗c,
1 1 1 1 1 1 1
所以⃗EF=⃗EB+⃗BA+⃗AF= ⃗CB−⃗AB+ ⃗AD= (⃗AB−⃗AC)−⃗AB+ ⃗AD=− ⃗a− ⃗b+ ⃗c,
2 2 2 2 2 2 2
1
因正四面体ABCD的棱长为1,则⃗a⋅⃗b=⃗b⋅⃗c=⃗c⋅⃗a=|⃗c||⃗a|cos60∘= ,
2
1 1 √2
所以|⃗EF|= √(−⃗a−⃗b+⃗c) 2= √⃗a2+⃗b2+⃗c2+2⃗a⋅⃗b−2⃗b⋅⃗c−2⃗c⋅⃗a=
.
2 2 2
1 1 1 1 1
(2)依题意,⃗GH=⃗GA+⃗AD+⃗DH=− ⃗a+⃗c+ (⃗b−⃗c)=− ⃗a+ ⃗b+ ⃗c,
2 2 2 2 2
1
因正四面体ABCD的棱长为1,有⃗c⋅⃗a=|⃗c||⃗a|cos60∘= ,
2
1 1 1 1
因此⃗EF⋅⃗GH=− (⃗a+⃗b−⃗c)⋅(− )(⃗a−⃗b−⃗c)= [(⃗a−⃗c) 2−⃗b2 ]= (⃗a2+⃗c2−2⃗a⋅⃗c−⃗b2 )=0,
2 2 4 4
所以⃗EF⊥⃗GH,即⃗EF与⃗GH的夹角为90∘.
【变式6-1】(2023秋·上海浦东新·高三校考期末)如图,在圆柱中,底面直径AB等于母线A A .
1
学科网(北京)股份有限公司(1)若AB=2,求圆柱的侧面积;
(2)设AB与CD是底面互相垂直的两条直径,求异面直线AC与A B所成角的大小.
1
【解题思路】(1)由已知得到底面半径r以及母线l的值,代入公式即可求出;
(2)用向量⃗AB、⃗DC、⃗A A 来表示出⃗AC、⃗A B,进而求出它们的夹角,即可求出结果.
1 1
【解答过程】(1)由已知可得,底面半径r=1,母线l=A A =2,
1
所以圆柱的侧面积S=2πrl=4π.
(2)由已知可得,AB,CD,A A 两两垂直,且相等,
1
设AB=2,则OA=OC=1,AC=√OA2+OC2=√2,A B=√A A 2+AB2=2√2.
1 1
1 1
又⃗AC=⃗OC−⃗OA= ⃗DC+ ⃗AB, ⃗A B=⃗AB−⃗A A ,
2 2 1 1
则⃗AC⋅⃗A B= (1 ⃗DC+ 1 ⃗AB ) ⋅(⃗AB−⃗A A ) = 1 ⃗DC⋅⃗AB− 1 ⃗DC⋅⃗A A + 1 ⃗AB2− 1 ⃗AB⋅⃗A A
1 2 2 1 2 2 1 2 2 1
1
= ⃗AB2=2.
2
⃗AC⋅⃗A B 2 1
所以cos⟨⃗AC,⃗A B⟩= 1 = =
,
1 |⃗AC||⃗A B| √2×2√2 2
1
π
又0≤⟨⃗AC,⃗A B⟩≤π,所以 ⟨⃗AC,⃗A B⟩= ,
1 1 3
π
所以异面直线AC与A B所成角的大小为 .
1 3
【变式6-2】(2022秋·山东聊城·高二校考阶段练习)如图,在棱长为1的正四面体OABC中,M,N分别
是边OA,BC的中点,点G在MN上,且MG=2GN,设⃑OA=⃑a,⃑OB=⃑b,⃑OC=⃑c.
(1)试用向量⃑a,⃑b,⃑c表示向量⃑OG;
(2)求cos<⃑OG,⃑BA>.
学科网(北京)股份有限公司【解题思路】(1)根据平面向量基底运算即可得到结果.
(2)分别求出|⃑BA|,|⃑OG|,⃑BA⋅⃑OG的值,再结合向量的夹角公式即可求得结果.
【解答过程】(1)
1 2
⃑OG=⃑OM+⃑MG= ⃑OA+ (⃑MA+⃑AB+⃑BN)
2 3
1 2(1 1 ) 1 2[ 1 1 ]
= ⃑OA+ ⃑OA+⃑OB−⃑OA+ ⃑BC = ⃑OA+ ⃑OB− ⃑OA+ (⃑OC−⃑OB)
2 3 2 2 2 3 2 2
1 2(1 1 1 ) 1 1 1 1
= ⃑OA+ ⃑OB− ⃑OA+ ⃑OC = ⃑OA+ ⃑OB− ⃑OA+ ⃑OC
2 3 2 2 2 2 3 3 3
1 1 1 1 1 1
= ⃑OA+ ⃑OB+ ⃑OC= ⃑a+ ⃑b+ ⃑c
6 3 3 6 3 3
(2)
1
由题意知,|⃑a|=|⃑b|=|⃑c|=1,⃑a⋅⃑b=⃑a⋅⃑c=⃑b⋅⃑c= ,⃑BA=⃑a−⃑b,
2
则|⃑BA|=√(⃑a−⃑b) 2=√ |⃑a| 2 −2⃑a⋅⃑b+|⃑b| 2 =1,
|⃑OG|= √ (1 ⃑a+ 1 ⃑b+ 1 ⃑c ) 2 = √ 1 |⃑a| 2+ 1 |⃑b| 2 + 1 |⃑c| 2+ 1 ⃑a⋅⃑b+ 1 ⃑a⋅⃑c+ 2 ⃑b⋅⃑c= √17 ,
6 3 3 36 9 9 9 9 9 6
(1 1 1 )
⃑OG⋅⃑BA=(⃑a−⃑b)⋅ ⃑a+ ⃑b+ ⃑c
6 3 3
1 1 1 1 1 1 1
= ⃑a2+ ⃑a⋅⃑b+ ⃑a⋅⃑c− ⃑a⋅⃑b− ⃑b2− ⃑b⋅⃑c=− ,
6 3 3 6 3 3 12
⃑OG⋅⃑BA √17
所以cos<⃑OG,⃑BA>= =−
.
|⃑OG||⃑BA| 34
【变式6-3】(2023春·广西南宁·高二统考开学考试)已知在平行六面体ABCD−A B C D 中,AB=2,
1 1 1 1
π
A A =3,AD=1且∠DAB=∠BA A =∠DA A = .
1 1 1 3
(1)求DB 的长;
1
学科网(北京)股份有限公司(2)求向量⃗DB 与⃗AB夹角的余弦值.
1
【解题思路】(1)用空间的一个基底{⃗AB,⃗AD,⃗A A }表示向量⃗DB ,再利用空间向量数量积的运算律求
1 1
解作答.
(2)利用(1)中信息,结合空间向量的夹角公式计算作答.
【解答过程】(1)在平行六面体ABCD−A B C D 中,{⃗AB,⃗AD,⃗A A }为空间的一个基底,
1 1 1 1 1
π
因为AB=2,A A =3,AD=1且∠DAB=∠BA A =∠DA A = ,
1 1 1 3
π π π 3
则⃗AB⋅⃗AD=2×1×cos =1,⃗AB⋅⃗A A =2×3×cos =3,⃗AD⋅⃗A A =1×3×cos = ,
3 1 3 1 3 2
⃗DB =⃗DA+⃗AB+⃗BB =⃗AB−⃗AD+⃗A A ,
1 1 1
所以|⃗DB |=√⃗AB2+⃗AD2+⃗A A 2−2⃗AB⋅⃗AD−2⃗AD⋅⃗A A +2⃗AB⋅⃗A A
1 1 1 1
√ 3
= 22+12+32−2×1−2× +2×3=√15.
2
(2)由(1)知,⃗DB =⃗AB−⃗AD+⃗A A ,则⃗DB ⋅⃗AB=⃗AB2−⃗AB⋅⃗AD+⃗AB⋅⃗A A =22−1+3=6,
1 1 1 1
又|DB →
1
|=√15,所以向量⃗DB
1
与⃗AB夹角的余弦值cos〈⃗DB
1
,⃗AB〉=
|⃗D
⃗D
B
B 1
|
⋅
|
⃗A
⃗A
B
B|
=
√15
6
×2
= √
5
15 .
1
【题型7 利用空间向量基本定理证明垂直问题】
【例7】(2023·江苏·高二专题练习)已知空间四边形OABC中,∠AOB=∠BOC=∠AOC,且
OA=OB=OC,M,N分别是OA,BC的中点,G是MN的中点,求证:OG⊥BC.
【解题思路】取定基底向量⃑OA,⃑OB,⃑OC,并分别记为⃑a,⃑b,⃑c,再用基底表示出⃑OG和⃑BC,然后借助数量
积即可计算作答.
【解答过程】在空间四边形OABC中,令⃑OA=⃑a,⃑OB=⃑b,⃑OC=⃑c,则|⃑a|=|⃑b|=|⃑c|,
令∠AOB=∠BOC=∠AOC=θ,G是MN的中点,如图,
学科网(北京)股份有限公司1 1 1 1 1
则⃑OG= (⃑OM+⃑ON)= [ ⃑OA+ (⃑OB+⃑OC)]= (⃑a+⃑b+⃑c),⃑BC=⃑OC−⃑OB=⃑c−⃑b,
2 2 2 2 4
1 1
于是得⃑OG⋅⃑BC= (⃑a+⃑b+⃑c)⋅(⃑c−⃑b)= (⃑a⋅⃑c−⃑a⋅⃑b+⃑b⋅⃑c−⃑b2+⃑c2−⃑b⋅⃑c)
4 4
1
= (|⃑a|2cosθ−|⃑a|2cosθ−|⃑a|2+|⃑a|2 )=0,
4
因此,⃑OG⊥⃑BC,
所以OG⊥BC.
【变式7-1】(2023春·安徽合肥·高二校考开学考试)如图所示,三棱柱ABC−A B C 中,⃑CA=⃗a,
1 1 1
2π π
⃑CB=⃗b,⃑CC =⃗c,CA=CB=CC =1, ⟨⃗a,⃗b⟩=⟨⃗a,⃗c⟩= , ⟨⃗b,⃗c⟩= ,N是AB中点.
1 1 3 2
(1)用⃗a,⃗b,⃗c表示向量⃑A N;
1
(2)在线段C B 上是否存在点M,使AM⊥A N?若存在,求出M的位置,若不存在,说明理由.
1 1 1
【解题思路】(1)根据空间向量线性运算的几何意义进行求解即可;
(2)设⃑C M=λ⃑C B ,(λ∈[0,1]),用⃗a,⃗b,⃗c表示向量⃑AM,依题意可得⃑AM⋅⃑A N=0,根据空间
1 1 1 1
向量数量积的运算律求出λ,即可得解.
1
【解答过程】(1)解:因为N是AB中点,所以⃑AN= ⃑AB,
2
1
所以⃑A N=⃑A A+⃑AN=⃑C C+ ⃑AB
1 1 1 2
1 1 1
=−⃑CC + (⃑CB−⃑CA)=− ⃗a+ ⃗b−⃗c;
1 2 2 2
学科网(北京)股份有限公司(2)解:假设存在点M,使AM⊥A N,设⃑C M=λ⃑C B ,(λ∈[0,1]),
1 1 1 1
显然λ⃑C B =λ⃗b,⃑AM=⃑A A +⃑A C +⃑C M=⃗c−⃗a+λ⃗b,
1 1 1 1 1 1
因为AM⊥A N,所以⃑AM⋅⃑A N=0,
1 1
1 1
即(⃗c−⃗a+λ⃗b)⋅(− ⃗a+ ⃗b−⃗c)=0,
2 2
1 1 1 1 1 1
∴− ⃗c⋅⃗a+ ⃗c⋅⃗b−⃗c2+ ⃗a2− ⃗a⋅⃗b+⃗c⋅⃗a− λ⃗a⋅⃗b+ λ⃗b2−λ⃗b⋅⃗c=0
2 2 2 2 2 2
2π π
∵CA=CB=CC =1, ⟨⃗a,⃗b⟩=⟨⃗a,⃗c⟩= , ⟨⃗b,⃗c⟩= ,
1 3 2
1 1 1 1 1
∴ ⃗c⋅⃗a−⃗c2+ ⃗a2−( + λ)⃗a⋅⃗b+ λ⃗b2=0
2 2 2 2 2
1 1 1 1 1 1 1
即 ×1×1×(− )−12+ ×12−( + λ)×1×1×(− )+ λ⋅12=0,
2 2 2 2 2 2 2
2 2
解得λ= ,所以当C M= C B 时,AM⊥A N.
3 1 3 1 1 1
【变式7-2】(2022秋·全国·高二专题练习)已知四面体中三组相对棱的中点间的距离都相等,求证: 这个
四面体相对的棱两两垂直.
已知:如图,四面体ABCD,E,F,G,H,K,M分别为棱AB,BC,CD,DA,BD,AC
的中点,且|EG|=|FH|=|KM|求证 AB⊥CD,AC⊥BD,AD⊥BC.
【解题思路】设⃑AB=⃗a,⃑AC=⃗b,⃑AD=⃗c,由空间向量的运算证明AC⊥DB,AD⊥BC,AB⊥CD.
【解答过程】证明:设⃑AB=⃗a,⃑AC=⃗b,⃑AD=⃗c
1 1 1 1 1 1
则⃑EG=⃑AG−⃑AE= (⃑AC+⃑AD)− ⃑AB=− ⃗a+ ⃗b+ ⃗c= (−⃗a+⃗b+⃗c)
2 2 2 2 2 2
1 1 1 1 1
⃑FH=⃑AH−⃑AF= ⃑AD− (⃑AB+⃑AC)= ⃗c− (⃗a+⃗b)= (−⃗a−⃗b+⃗c),
2 2 2 2 2
学科网(北京)股份有限公司1 1 1 1 1
⃑KM=⃑AM−⃑AK= ⃑AC− (⃑AB+⃑AD)= ⃗b− (⃗a+⃗c)= (−⃗a+⃗b−⃗c),
2 2 2 2 2
|1 | |1 |
∵|⃑EG|=|⃑FH|,∴ (−⃗a+⃗b+⃗c) = (−⃗a−⃗b+⃗c) ,
2 2
∴(−⃗a+⃗b+⃗c) 2 =(−⃗a−⃗b+⃗c) 2 ,
∴⃗a2+⃗b2+⃗c2−2⃗a⋅⃗b−2⃗a⋅⃗c+2⃗b⋅⃗c=⃗a2+⃗b2+⃗c2+2⃗a⋅⃗b−2⃗a⋅⃗c−2⃗b⋅⃗c,
∴4⃗a⋅⃗b=4⃗b⋅⃗c,∴⃗a⋅⃗b−⃗b⋅⃗c=0,∴⃗b⋅(⃗a−⃗c)=0
又⃗b=⃑AC,⃗a−⃗c=⃑DB,∴⃑AC⋅⃑DB=0
∴⃑AC⊥⃑DB,∴AC⊥DB,同理可证AD⊥BC,AB⊥CD,
∴这个四面体相对的棱两两垂直.
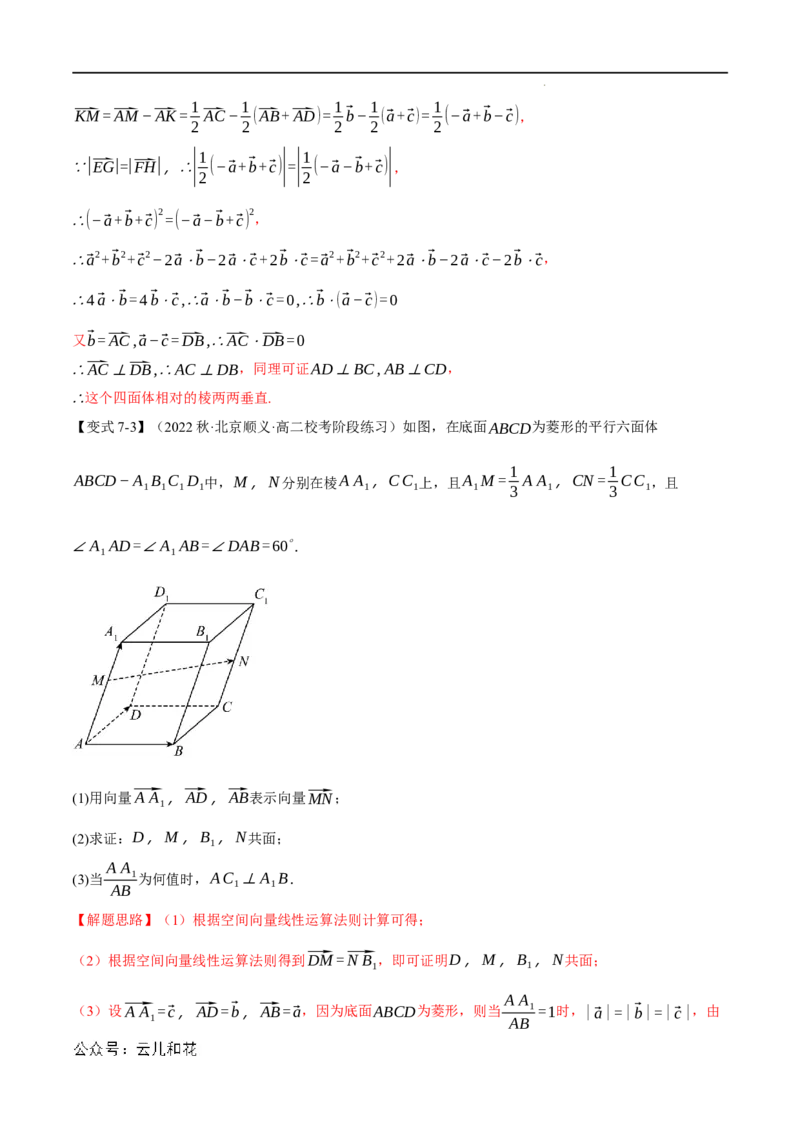
【变式7-3】(2022秋·北京顺义·高二校考阶段练习)如图,在底面ABCD为菱形的平行六面体
1 1
ABCD−A B C D 中,M,N分别在棱A A ,CC 上,且A M= A A ,CN= CC ,且
1 1 1 1 1 1 1 3 1 3 1
∠A AD=∠A AB=∠DAB=60∘.
1 1
(1)用向量⃗A A ,⃗AD,⃗AB表示向量⃗MN;
1
(2)求证:D,M,B ,N共面;
1
A A
(3)当 1为何值时,AC ⊥A B.
AB 1 1
【解题思路】(1)根据空间向量线性运算法则计算可得;
(2)根据空间向量线性运算法则得到⃗DM=⃗NB ,即可证明D,M,B ,N共面;
1 1
A A
(3)设⃗A A =⃗c,⃗AD=⃗b,⃗AB=⃗a,因为底面ABCD为菱形,则当 1=1时,|⃗a|=|⃗b|=|⃗c|,由
1 AB
学科网(北京)股份有限公司,即可得出答案.
⃗AC ⋅⃗A B=(⃗a+⃗b+⃗c)⋅(⃗a−⃗c)=0
1 1
2 1 1
【解答过程】(1)⃗MN=⃗MA+⃗AB+⃗BC+⃗CN=− ⃗A A +⃗AB+⃗BC+ ⃗A A =⃗AB+⃗AD− ⃗A A .
3 1 3 1 3 1
2 2
(2)证明:∵⃗DM=⃗AM−⃗AD= ⃗A A −⃗AD,⃗NB =⃗C B −⃗C N= ⃗A A −⃗AD,
3 1 1 1 1 1 3 1
∴⃗DM=⃗NB ,∴D,M,B ,N共面.
1 1
A A
(3)当 1=1,AC ⊥A B,
AB 1 1
证明:设⃗A A =⃗c,⃗AD=⃗b,⃗AB=⃗a,
1
A A
∵底面ABCD为菱形,则当 1=1时,|⃗a|=|⃗b|=|⃗c|,
AB
∵⃗AC =⃗AB+⃗BC+⃗CC =⃗a+⃗b+⃗c,⃗A B=⃗AB−⃗A A =⃗a−⃗c,
1 1 1 1
∠A AD=∠A AB=∠DAB=60∘,
1 1
∴⃗AC ⋅⃗A B=(⃗a+⃗b+⃗c)⋅(⃗a−⃗c)=⃗a2+⃗a⋅⃗b−⃗b⋅⃗c−⃗c2=0,
1 1
∴AC ⊥A B.
1 1
【题型8 利用空间向量基本定理求距离(长度)问题】
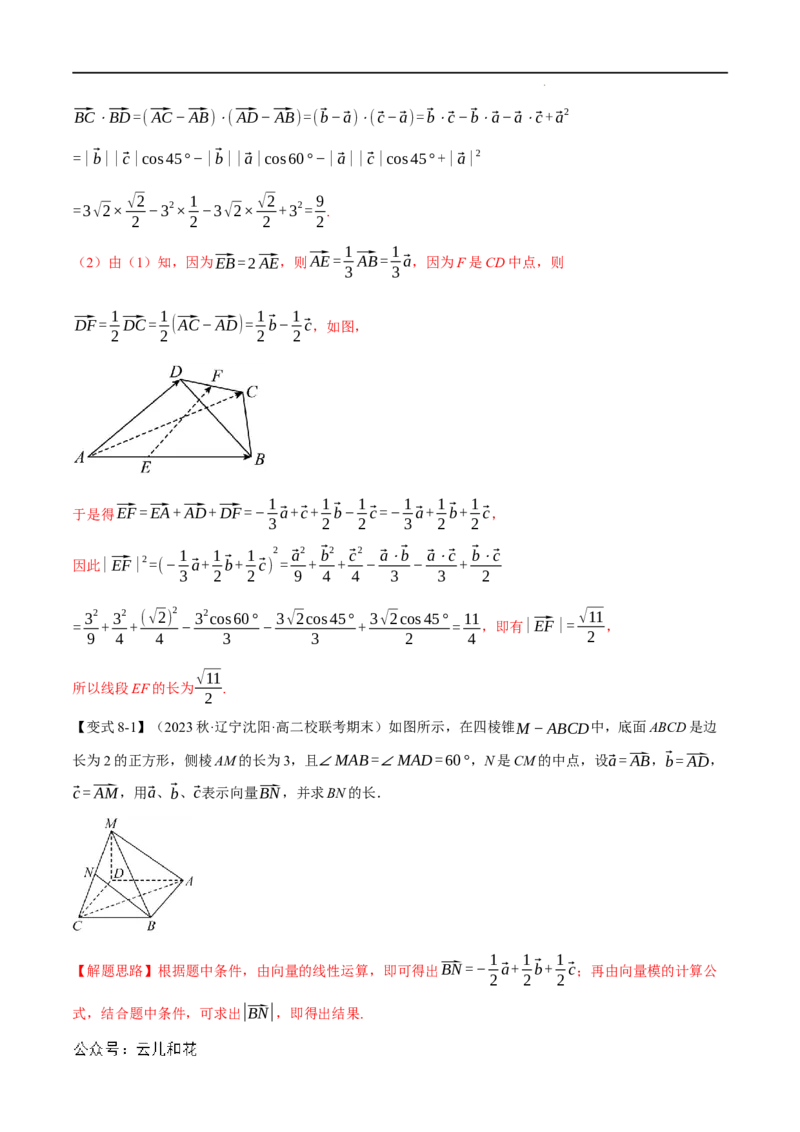
【例8】(2023秋·福建三明·高二统考期末)如图,在四面体ABCD中,∠BAC=60°,
∠BAD=∠CAD=45°,AD=√2,AB=AC=3.
(1)求⃗BC⋅⃗BD的值;
(2)已知F是线段CD中点,点E满足⃗EB=2⃗AE,求线段EF的长.
【解题思路】(1)取⃗AB,⃗AC,⃗AD为空间的一个基底,表示出⃗BC,⃗BD,再利用空间向量数量积求解作答.
(2)利用(1)中的信息,利用空间向量数量积计算空间向量的模作答.
【解答过程】(1)在四面体ABCD中,设⃗AB=⃗a,⃗AC=⃗b,⃗AD=⃗c,则|⃗a|=|⃗b|=3,|⃗c|=√2,
〈⃗a,⃗b〉=∠BAC=60°,〈⃗a,⃗c〉=∠BAD=45°,〈⃗b,⃗c〉=∠CAD=45°,
学科网(北京)股份有限公司⃗BC⋅⃗BD=(⃗AC−⃗AB)⋅(⃗AD−⃗AB)=(⃗b−⃗a)⋅(⃗c−⃗a)=⃗b⋅⃗c−⃗b⋅⃗a−⃗a⋅⃗c+⃗a2
=|⃗b||⃗c|cos45°−|⃗b||⃗a|cos60°−|⃗a||⃗c|cos45°+|⃗a|2
√2 1 √2 9
=3√2× −32× −3√2× +32= .
2 2 2 2
1 1
(2)由(1)知,因为⃗EB=2⃗AE,则⃗AE= ⃗AB= ⃗a,因为F是CD中点,则
3 3
1 1 1 1
⃗DF= ⃗DC= (⃗AC−⃗AD)= ⃗b− ⃗c,如图,
2 2 2 2
1 1 1 1 1 1
于是得⃗EF=⃗EA+⃗AD+⃗DF=− ⃗a+⃗c+ ⃗b− ⃗c=− ⃗a+ ⃗b+ ⃗c,
3 2 2 3 2 2
1 1 1 2 ⃗a2 ⃗b2 ⃗c2 ⃗a⋅⃗b ⃗a⋅⃗c ⃗b⋅⃗c
因此|⃗EF|2=(− ⃗a+ ⃗b+ ⃗c) = + + − − +
3 2 2 9 4 4 3 3 2
32 32 (√2) 2 32cos60° 3√2cos45° 3√2cos45° 11 √11
= + + − − + = ,即有|⃗EF|= ,
9 4 4 3 3 2 4 2
√11
所以线段EF的长为 .
2
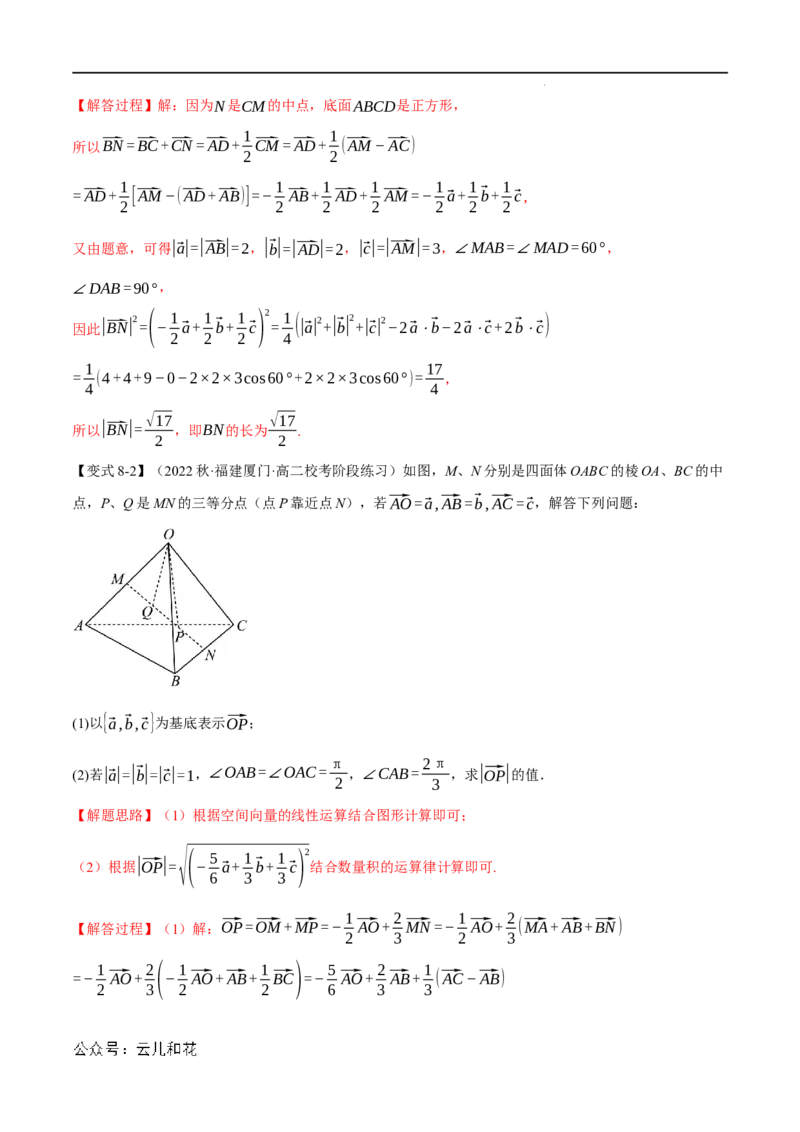
【变式8-1】(2023秋·辽宁沈阳·高二校联考期末)如图所示,在四棱锥M−ABCD中,底面ABCD是边
长为2的正方形,侧棱AM的长为3,且∠MAB=∠MAD=60°,N是CM的中点,设⃗a=⃑AB,⃗b=⃑AD,
⃗c=⃑AM,用⃗a、⃗b、⃗c表示向量⃑BN,并求BN的长.
1 1 1
【解题思路】根据题中条件,由向量的线性运算,即可得出⃑BN=− ⃗a+ ⃗b+ ⃗c;再由向量模的计算公
2 2 2
式,结合题中条件,可求出|⃑BN|,即得出结果.
学科网(北京)股份有限公司【解答过程】解:因为N是CM的中点,底面ABCD是正方形,
1 1
所以⃑BN=⃑BC+⃑CN=⃑AD+ ⃑CM=⃑AD+ (⃑AM−⃑AC)
2 2
1 1 1 1 1 1 1
=⃑AD+ [⃑AM−(⃑AD+⃑AB)]=− ⃑AB+ ⃑AD+ ⃑AM=− ⃗a+ ⃗b+ ⃗c,
2 2 2 2 2 2 2
又由题意,可得|⃗a|=|⃑AB|=2,|⃗b|=|⃑AD|=2,|⃗c|=|⃑AM|=3,∠MAB=∠MAD=60°,
∠DAB=90°,
因此|⃑BN| 2 = ( − 1 ⃗a+ 1 ⃗b+ 1 ⃗c ) 2 = 1 ( |⃗a| 2+|⃗b| 2 +|⃗c| 2 −2⃗a⋅⃗b−2⃗a⋅⃗c+2⃗b⋅⃗c )
2 2 2 4
1 17
= (4+4+9−0−2×2×3cos60°+2×2×3cos60°)= ,
4 4
√17 √17
所以|⃑BN|= ,即BN的长为 .
2 2
【变式8-2】(2022秋·福建厦门·高二校考阶段练习)如图,M、N分别是四面体OABC的棱OA、BC的中
点,P、Q是MN的三等分点(点P靠近点N),若⃗AO=⃗a,⃗AB=⃗b,⃗AC=⃗c,解答下列问题:
(1)以{⃗a,⃗b,⃗c}为基底表示⃗OP;
π 2π
(2)若|⃗a|=|⃗b|=|⃗c|=1,∠OAB=∠OAC= ,∠CAB= ,求|⃗OP|的值.
2 3
【解题思路】(1)根据空间向量的线性运算结合图形计算即可;
(2)根据|⃗OP|= √ ( − 5 ⃗a+ 1 ⃗b+ 1 ⃗c ) 2 结合数量积的运算律计算即可.
6 3 3
1 2 1 2
【解答过程】(1)解:⃗OP=⃗OM+⃗MP=− ⃗AO+ ⃗MN=− ⃗AO+ (⃗MA+⃗AB+⃗BN)
2 3 2 3
=− 1 ⃗AO+ 2( − 1 ⃗AO+⃗AB+ 1 ⃗BC ) =− 5 ⃗AO+ 2 ⃗AB+ 1 (⃗AC−⃗AB)
2 3 2 2 6 3 3
学科网(北京)股份有限公司5 1 1 5 1 1
=− ⃗AO+ ⃗AB+ ⃗AC=− ⃗a+ ⃗b+ ⃗c;
6 3 3 6 3 3
(2)解:|⃗OP|= √ ( − 5 ⃗a+ 1 ⃗b+ 1 ⃗c ) 2
6 3 3
√25 1 1 5 5 2
= ⃗a2+ ⃗b2+ ⃗c2− ⃗a⋅⃗b− ⃗a⋅⃗c+ ⃗c⋅⃗b
36 9 9 9 9 9
√25 1 1 2 ( 1) √29
= + + −0−0+ ×1×1× − = .
36 9 9 9 2 6
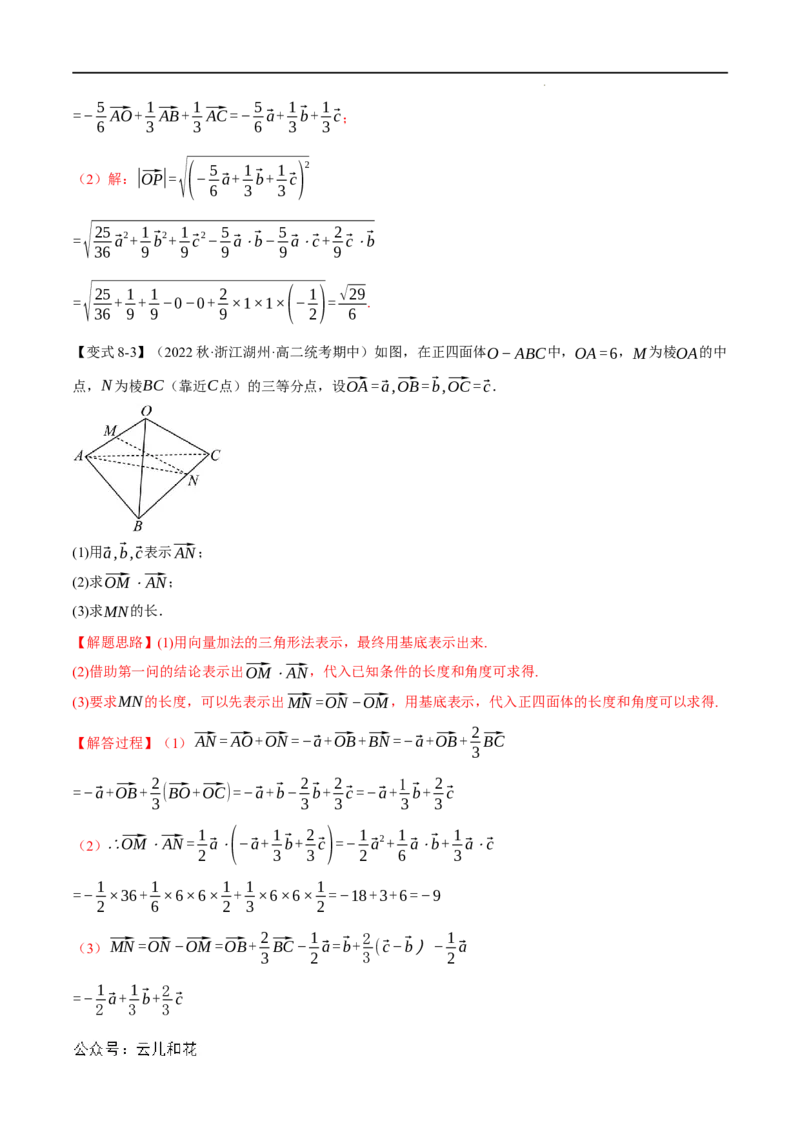
【变式8-3】(2022秋·浙江湖州·高二统考期中)如图,在正四面体O−ABC中,OA=6,M为棱OA的中
点,N为棱BC(靠近C点)的三等分点,设⃗OA=⃗a,⃗OB=⃗b,⃗OC=⃗c.
(1)用⃗a,⃗b,⃗c表示⃗AN;
(2)求⃗OM⋅⃗AN;
(3)求MN的长.
【解题思路】(1)用向量加法的三角形法表示,最终用基底表示出来.
(2)借助第一问的结论表示出⃗OM⋅⃗AN,代入已知条件的长度和角度可求得.
(3)要求MN的长度,可以先表示出⃗MN=⃗ON−⃗OM,用基底表示,代入正四面体的长度和角度可以求得.
2
【解答过程】(1)⃗AN=⃗AO+⃗ON=−⃗a+⃗OB+⃗BN=−⃗a+⃗OB+ ⃗BC
3
2 2 2 1 2
=−⃗a+⃗OB+ (⃗BO+⃗OC)=−⃗a+⃗b− ⃗b+ ⃗c=−⃗a+ ⃗b+ ⃗c
3 3 3 3 3
(2)∴⃗OM⋅⃗AN= 1 ⃗a⋅ ( −⃗a+ 1 ⃗b+ 2 ⃗c ) =− 1 ⃗a2+ 1 ⃗a⋅⃗b+ 1 ⃗a⋅⃗c
2 3 3 2 6 3
1 1 1 1 1
=− ×36+ ×6×6× + ×6×6× =−18+3+6=−9
2 6 2 3 2
2 1 2 1
(3)⃗MN=⃗ON−⃗OM=⃗OB+ ⃗BC− ⃗a=⃗b+ (⃗c−⃗b)− ⃗a
3 2 3 2
1 1 2
=− ⃗a+ ⃗b+ ⃗c
2 3 3
学科网(北京)股份有限公司∴|⃗MN|= √ ( − 1 ⃗a+ 1 ⃗b+ 2 ⃗c ) 2
2 3 3
= √1 ⃗a2+ 1 ⃗b2+ 4 ⃗c2+2⋅ ( − 1) ⋅ 1 ⃗a⋅⃗b+2⋅ ( − 1) ⋅ 2 ⃗a⋅⃗c+2⋅ 1 ⋅ 2 ⃗b⋅⃗c
4 9 9 2 3 2 3 3 3
√1 1 4
= ×36+ ×36+ ×36−6−12+8 =√19.
4 9 9
学科网(北京)股份有限公司