文档内容
专题 1.4 空间向量及其运算的坐标表示【八大题型】
【人教A版(2019)】
【题型1 求空间点的坐标】......................................................................................................................................1
【题型2 空间向量运算的坐标表示】......................................................................................................................3
【题型3 空间向量数量积运算的坐标表示】.........................................................................................................4
【题型4 根据空间向量的坐标运算求参数】.........................................................................................................6
【题型5 空间向量模长的坐标表示】......................................................................................................................8
【题型6 空间向量平行的坐标表示】....................................................................................................................11
【题型7 空间向量垂直的坐标表示】....................................................................................................................13
【题型8 空间向量夹角余弦的坐标表示】...........................................................................................................15
【知识点1 空间直角坐标系】
1.空间直角坐标系
(1)空间直角坐标系及相关概念
①空间直角坐标系:在空间选定一点O和一个单位正交基底,以O为原点,分别以i,j,k 的方向为
正方向,以它们的长为单位长度建立三条数轴:x轴、y轴、z轴,它们都叫做坐标轴,这时我们就建立了
一个空间直角坐标系O-xyz.
②相关概念:O叫做原点,i,j,k 都叫做坐标向量,通过每两个坐标轴的平面叫做坐标平面,分别
称为Oxy平面、Oyz平面、Ozx平面,它们把空间分成八个部分.
(2)右手直角坐标系
在空间直角坐标系中,让右手拇指指向 x轴的正方向,食指指向y轴的正方向,如果中指指向z轴的
正方向,则称这个坐标系为右手直角坐标系.
2.空间一点的坐标
在空间直角坐标系O-xyz中,i,j,k为坐标向量,对空间任意一点A,对应一个向量OA,且点A的位
置由向量OA唯一确定,由空间向量基本定理,存在唯一的有序实数组(x,y,z),使OA=xi+yj+zk.在单位
正交基底 {i,j,k}下与向量 OA 对应的有序实数组(x,y,z)叫做点A在此空间直角坐标系中的坐标,记
作A(x,y,z),其中x叫做点A的横坐标,y叫做点A的纵坐标,z叫做点A的竖坐标.
【题型1 求空间点的坐标】
【例1】(2023春·山东青岛·高二校联考期中)空间直角坐标系中,已知A(−1,1,3),则点A关于yOz平面
的对称点的坐标为( )
学科网(北京)股份有限公司A.(1,1,−3) B.(−1,−1,−3) C.(1,1,3) D.(−1,−1,3)
【解题思路】根据空间直角坐标系中点关于yOz平面的对称点的特征可得答案.
【解答过程】根据空间直角坐标系的对称性可得A(−1,1,3)关于yOz平面的对称点的坐标为(1,1,3),
故选:C.
【变式1-1】(2023秋·陕西宝鸡·高二统考期末)已知点A(3,−1,0),若向量⃗AB=(−1,6,−3),则点B的
坐标是( )
A.(1,−6,3) B.(5,4,−3) C.(−1,6,−3) D.(2,5,−3)
【解题思路】设B(x,y,z),表达出⃗AB=(x−3,y+1,z),从而列出方程组,求出点B的坐标为(2,5,−3).
【解答过程】设B(x,y,z),则⃗AB=(x−3,y+1,z),
因为⃗AB=(−1,6,−3),所以x−3=−1,y+1=6,z=−3,解得:x=2,y=5,z=−3,
故点B的坐标为(2,5,−3).
故选:D.
【变式1-2】(2023秋·北京怀柔·高二统考期末)若点A(1,2,3),点B(4,−1,0),且⃗AC=2⃗CB,则点C的
坐标为( )
A.(3,0,1) B.(2,1,2)
(3 3 3) (5 1 3)
C. ,− ,− D. , ,
2 2 2 2 2 2
【解题思路】设C(x,y,z),根据⃗AC=2⃗CB列方程组即可求解.
【解答过程】设C(x,y,z),则⃗AC=(x−1,y−2,z−3),⃗CB=(4−x,−1−y,−z),
因为⃗AC=2⃗CB,所以¿,解得¿.
故点C的坐标为(3,0,1).
故选:A.
【变式1-3】(2023·高二单元测试)在空间直角坐标系中,已知点P(x,y,z)下列叙述中正确的是( )
①点P关于x轴的对称点是P (x,−y,z)
1
②点P关于yOz平面的对称点是P (−x,y,z)
2
③点P关于y轴的对称点是P (x,−y,z)
3
④点P关于原点的对称点是P (−x,−y,−z)
4
A.①② B.①③ C.②④ D.②③
【解题思路】根据空间坐标的对称性进行判断即可.
【解答过程】点P关于x轴的对称点的坐标是(x,−y,−z),故①错误;
点P关于yOz平面的对称点的坐标是(−x,y,z),则②正确;
学科网(北京)股份有限公司点P关于y轴的对称点的坐标是(−x,y,−z),则③错误;
点P关于原点的对称点的坐标是(−x,−y,−z),故④正确,
故正确的命题的序号是②④,
故选:C.
【知识点2 空间向量的坐标运算】
1.空间向量的坐标
在空间直角坐标系Oxyz中,给定向量a,作OA=a.由空间向量基本定理,存在唯一的有序实数组(x,
y,z),使a=xi+yj+zk.有序实数组(x,y,z)叫做a在空间直角坐标系O-xyz中的坐标,上式可简记作a=
(x,y,z).
2.空间向量的坐标运算
设a=(a,a,a),b=(b,b,b),有
1 2 3 1 2 3
向量运算 向量表示 坐标表示
加法 a+b a+b=(a+b,a+b,a+b)
1 1 2 2 3 3
减法 a-b a-b=(a-b,a-b,a-b)
1 1 2 2 3 3
数乘 λa λa=(λa,λa,λa),λ∈R
1 2 3
数量积 a·b a·b=ab+ab+ab
1 1 2 2 3 3
【题型2 空间向量运算的坐标表示】
【例2】(2023春·全国·高二校联考开学考试)已知向量⃗a=(3,−4,2),⃗b=(2,−3,1),则⃗a−2⃗b=( )
A.(7,−10,4) B.(5,−7,3) C.(1,−1,1) D.(−1,2,0)
【解题思路】根据向量线性运算的坐标表示得出答案.
【解答过程】⃗a−2⃗b=(3−2×2,−4−2×(−3),2−2×1)=(−1,2,0),
故选:D.
【变式2-1】(2023秋·江西吉安·高二校考期末)已知向量⃗AB=(2,3,1),⃗AC=(4,5,3),那么⃗BC=(
)
A.(−2,−2,−2) B.(8,15,3)C.(6,8,4) D.(2,2,2)
【解题思路】利用向量减法的法则及坐标运算即可求解.
【解答过程】因为⃗AB=(2,3,1),⃗AC=(4,5,3),
所以⃗BC=⃗AC−⃗AB=(4−2,5−3,3−1)=(2,2,2).
故选:D.
1
【变式2-2】(2022·全国·高二专题练习)已知向量⃗a=(2,3,−4),⃗b=(−4,−3,−2),⃗b= ⃗c−2⃗a,则⃗c=
2
学科网(北京)股份有限公司( )
A.(0,3,−6) B.(0,6,−20) C.(0,6,−6) D.(6,6,−6)
【解题思路】推导出⃗c=4⃗a+2⃗b,利用向量坐标运算法则直接求解.
1
【解答过程】∵向量⃗a=(2,3,−4),⃗b=(−4,−3,−2),⃗b= ⃗c−2⃗a,
2
∴⃗c=4⃗a+2⃗b=(8,12,−16)+(−8,−6,−4)=(0,6,−20).
故选:B.
【变式2-3】(2022秋·河南信阳·高二校考阶段练习)在空间四边形ABCD中,若向量⃑AB=(﹣3,5,
2),⃑CD=(﹣7,-1,﹣4),点E,F分别为线段BC,AD的中点,则⃑EF的坐标为( )
A.(2,3,3) B.(﹣2,﹣3,﹣3)
C.(5,﹣2,1) D.(﹣5,2,﹣1)
【解题思路】根据空间向量的加法减法运算及三角形中线的性质求解.
【解答过程】如图,取AC中点M,连接ME,MF, 如图,
1 3 5 1 7 1
则⃑ME= ⃑AB=(− , ,1), ⃑MF= ⃑CD=(− ,− ,−2),
2 2 2 2 2 2
而⃑EF=⃑MF−⃑ME=(−2,−3,−3),
故选:B.
【题型3 空间向量数量积运算的坐标表示】
【例3】(2022·全国·高二专题练习)若A(2,−4,−1),B(−1,5,1),C(3,−4,1),则⃗CA⋅⃗CB=( )
A.-11 B.3 C.4 D.15
【解题思路】先求出⃗CA,⃗CB的坐标表示,再利用向量数量积的坐标表示计算即可
学科网(北京)股份有限公司【解答过程】由已知,⃗CA=(2−3,−4−(−4),−1−1)=(−1,0,−2),
⃗CB=(−1−3,5−(−4),1−1)=(−4,9,0),
∴⃗CA⋅⃗CB=4+0+0=4.
故选:C.
【变式3-1】(2023春·高二课时练习)若 ,则 的值为( )
⃗a=(2,3,2),⃗b=(1,2,2),⃗c=(−1,2,2) (⃗a−⃗b)⋅⃗c
A.−1 B.0 C.1 D.2
【解题思路】直接利用数量积的坐标运算即可求得.
【解答过程】因为 ,
⃗a=(2,3,2),⃗b=(1,2,2),⃗c=(−1,2,2)
所以 .
(⃗a−⃗b)⋅⃗c=(1,1,0)⋅(−1,2,2)=−1+2+0=1
故选:C.
【变式3-2】(2023春·山东济宁·高三校考阶段练习)已知棱长为1的正方体ABCD−A B C D 的上底
1 1 1 1
面A B C D 的中心为O ,则⃑AO ⋅⃑AC 的值为( )
1 1 1 1 1 1 1
A.-1 B.0 C.1 D.2
【解题思路】建立空间直角坐标系,利用向量法计算出⃑AO ⋅⃑AC .
1 1
【解答过程】建立如图所示空间直角坐标系,
(1 1 )
A(1,0,0),O , ,1 ,C (0,1,1),
1 2 2 1
( 1 1 )
⃑AO = − , ,1 ,⃑AC =(−1,1,1),
1 2 2 1
( 1 1 ) 1 1
⃑AO ⋅⃑AC = − , ,1 ⋅(−1,1,1)= + +1=2
1 1 2 2 2 2
故选:D.
学科网(北京)股份有限公司【变式3-3】(2022春·广西桂林·高二校考期中)已知正六棱柱ABCDEF−A B C D E F 的底面边长
1 1 1 1 1 1
为1,P是正六棱柱内(不含表面)的一点,则⃗AP⋅⃗AB的取值范围是( )
1 3 3 1
A.(− , ) B.(− , )
2 2 2 2
1 3
C.(− ,1) D.(0, )
2 2
1 3
【解题思路】建立空间直角坐标系,设P(x,y,z),由正六边形的性质可知− 的值;
2
(2)若 ,求实数 的值.
(k⃗a+⃗b)∥(⃗a−3⃗b) k
【解题思路】(1)利用空间向量夹角公式的坐标运算直接求解;(2)根据两向量的共线定理,利用坐标运算求
解.
1
【解答过程】(1)由已知可得⃗c= ⃗b=(−1,1,2),⃗a=(1,4,−2),
2
⃗a⋅⃗c 1×(−1)+4×1+(−2)×2 −1 √14
∴cos<⃗a,⃗c>= = = =− .
|⃗a||⃗c| √1+16+4×√1+1+4 √21√6 42
(2) , ,
k⃗a+⃗b=(k−2,4k+2,−2k+4) ⃗a−3⃗b=(7,−2,−14)
∵ ,∴存在实数 使得 ,
(k⃗a+⃗b)∥(⃗a−3⃗b) m k⃗a+⃗b=m(⃗a−3⃗b)
1
∴k−2=7m,4k+2=−2m,−2k+4=−14m,联立解得k=− .
3
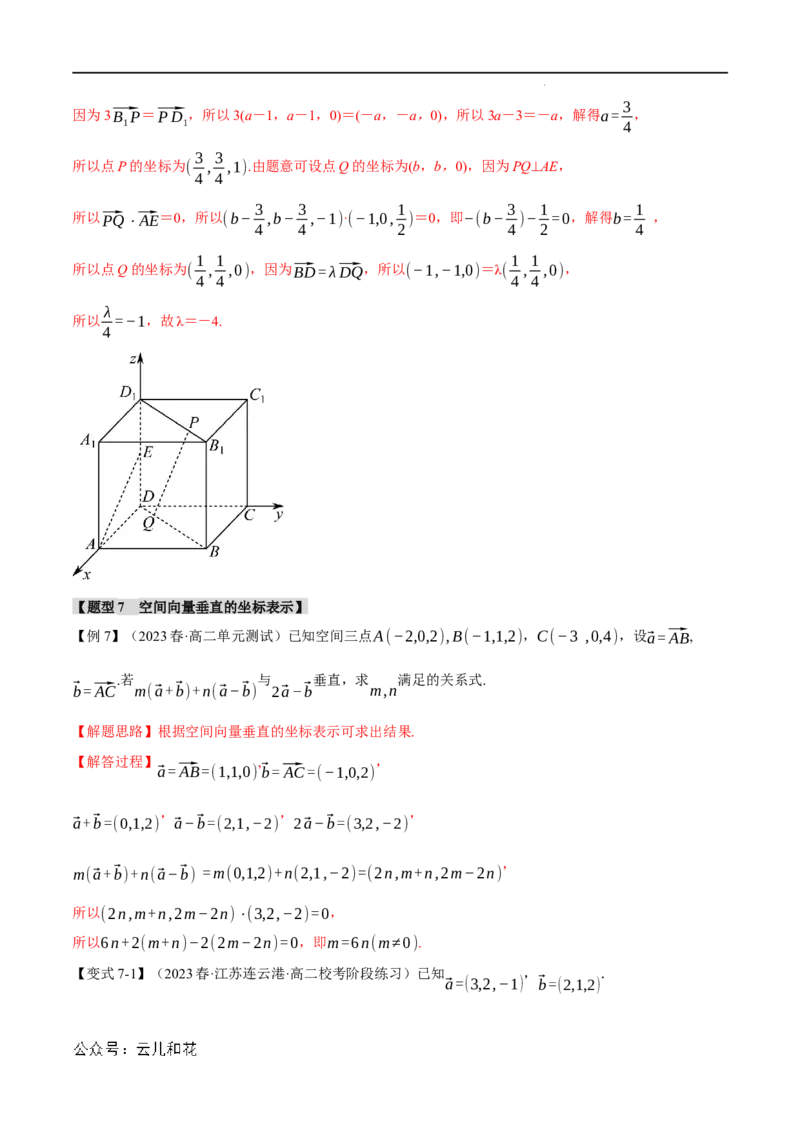
【变式6-3】(2022·高二课时练习)正方体ABCDABC D 中,E是棱DD的中点,P、Q分别为线段
1 1 1 1 1
BD,BD上的点,且3 = ,若PQ⊥AE, =λ ,求λ的值.
1 1 ⃗B P ⃗PD ⃗BD ⃗DQ
1 1
【解题思路】建立空间直角坐标系,设正方体棱长为1,求出A,E,B,B ,D 的坐标,设点P的坐标为
1 1
(a,a,1)和Q的坐标为(b,b,0),结合已知向量共线和向量垂直即可求出未知数的值,从而求出Q的坐
标,进而可求出λ.
【解答过程】以D为原点, , , 的方向分别为x轴,y轴,z轴的正方向,
⃗DA ⃗DC ⃗DD
1
1
建立空间直角坐标系,设正方体棱长为1,则A(1,0,0),E(0,0, ),B(1,1,0),
2
B(1,1,1),D(0,0,1),由题意,可设点P的坐标为(a,a,1),
1 1
学科网(北京)股份有限公司3
因为3⃗B P=⃗PD ,所以3(a-1,a-1,0)=(-a,-a,0),所以3a-3=-a,解得a= ,
1 1 4
3 3
所以点P的坐标为( , ,1).由题意可设点Q的坐标为(b,b,0),因为PQ⊥AE,
4 4
3 3 1 3 1 1
所以⃗PQ⋅⃗AE=0,所以(b− ,b− ,−1)·(−1,0, )=0,即−(b− )− =0,解得b= ,
4 4 2 4 2 4
1 1 1 1
所以点Q的坐标为( , ,0),因为⃗BD=λ⃗DQ,所以(−1,−1,0)=λ( , ,0),
4 4 4 4
λ
所以 =−1,故λ=-4.
4
【题型7 空间向量垂直的坐标表示】
【例7】(2023春·高二单元测试)已知空间三点A(−2,0,2),B(−1,1,2),C(−3 ,0,4),设⃗a=⃗AB,
.若 与 垂直,求 满足的关系式.
⃗b=⃗AC m(⃗a+⃗b)+n(⃗a−⃗b) 2⃗a−⃗b m,n
【解题思路】根据空间向量垂直的坐标表示可求出结果.
【解答过程】 , ,
⃗a=⃗AB=(1,1,0)⃗b=⃗AC=(−1,0,2)
, , ,
⃗a+⃗b=(0,1,2) ⃗a−⃗b=(2,1,−2) 2⃗a−⃗b=(3,2,−2)
,
m(⃗a+⃗b)+n(⃗a−⃗b) =m(0,1,2)+n(2,1,−2)=(2n,m+n,2m−2n)
所以(2n,m+n,2m−2n)⋅(3,2,−2)=0,
所以6n+2(m+n)−2(2m−2n)=0,即m=6n(m≠0).
【变式7-1】(2023春·江苏连云港·高二校考阶段练习)已知 , .
⃗a=(3,2,−1) ⃗b=(2,1,2)
学科网(北京)股份有限公司(1)求 ;
(⃗a−⃗b)⋅(⃗a+2⃗b)
(2)当 时,求实数k的值.
(⃗a−⃗b)⊥(⃗a+k⃗b)
【解题思路】(1)根据空间向量的运算,先求出⃗a−⃗b,⃗a+2⃗b,然后计算数量积;
(2)根据空间向量的运算,先求出⃗a−⃗b,⃗a+k⃗b,根据垂直关系可知它们数量积为0,据此计算.
【解答过程】(1)因为 , ,
⃗a=(3,2,−1) ⃗b=(2,1,2)
所以 , ,
⃗a−⃗b=(1,1,−3) ⃗a+2⃗b=(3,2,−1)+2(2,1,2)=(7,4,3)
所以
(⃗a−⃗b)⋅(⃗a+2⃗b)=1×7+1×4+(−3)×3=2
(2)因为 , ,
⃗a=(3,2,−1) ⃗b=(2,1,2)
所以 ,由(1) ,
⃗a+k⃗b=(3,2,−1)+k(2,1,2)=(3+2k,2+k,−1+2k) ⃗a−⃗b=(1,1,−3)
因为 ,所以 ,
(⃗a−⃗b)⊥(⃗a+k⃗b) (⃗a−⃗b)⋅(⃗a+k⃗b)=0
8
所以3+2k+2+k−3(2k−1)=0,解得k= .
3
【变式7-2】(2023春·江苏连云港·高二校联考期中)已知空间中三点A(2,0,−2),B(1,−1,3),
C(3,0,1),设⃗a=⃗AB,⃗b=⃗AC.
(1)若|⃗c|=3,且⃗c∥⃗BC,求向量⃗c;
(2)已知向量⃗a+k⃗b与⃗b互相垂直,求k的值.
【解题思路】(1)由⃗c∥⃗BC可得存在非零实数m,使得⃗c=m⃗BC,根据向量的坐标运算结合|⃗c|=3,即可
求解;
(2)根据向量垂直的条件即可解答.
【解答过程】(1)∵A(2,0,−2),B(1,−1,3),C(3,0,1),
∴⃗BC=(3,0,1)−(1,−1,3)=(2,1,−2),
又|⃗c|=3,且⃗c∥⃗BC,
∴存在非零实数m,使得⃗c=m⃗BC=(2m,m,−2m),
∴ ,
|⃗c|=√(2m)2+(m)2+(−2m)2=3
∴m=±1,
学科网(北京)股份有限公司∴⃗c=(2,1,−2)或⃗c=(− 2,)−;1,2
(2)⃗a=⃗AB=(− 1,)−,1⃗b,5=⃗AC=(1,0,3),
∴ ,
⃗a+k⃗b=(−1+k,−1,5+3 k)
∵向量⃗a+k⃗b与⃗b互相垂直,
7
∴(⃗a+k⃗b)⋅⃗b=−1+ k+0+3(5+3k)=0,解得k=− ,
5
7
故k=− .
5
【变式7-3】(2023秋·江西吉安·高二校考期末)已知 , ,点 ,
⃗a=(1,−4,5) ⃗b=(−2,3,2) A(−3,−2,3)
B(−2,−3,2).
(1)求 的值.
|2⃗a+⃗b|
(2)在线段AB上,是否存在一点E,使得⃗OE⊥⃗b?若存在,求出点E的坐标;若不存在,请说明理由.
(O为坐标原点)
【解题思路】(1)利用空间向量的线性运算及模的运算公式即可得解;
(2)利用空间向量共线定理得到⃗OE关于λ的关系式,再由空间向量垂直的坐标表示求得λ,从而得到点E
的坐标.
【解答过程】(1)因为 , ,
⃗a=(1,−4,5) ⃗b=(−2,3,2)
所以 ,
2⃗a+⃗b=2×(1,−4,5)+(−2,3,2)=(2,−8,10)+(−2,3,2)=(0,−5,12)
则 .
|2⃗a+⃗b|=√02+(−5) 2+122=13
(2)假设线段AB上存在一点E,使得⃗OE⊥⃗b,则设⃗AE=λ⃗AB(0≤λ≤1),
因为A(−3,−2,3),B(−2,−3,2),所以⃗AB=(−2,−3,2)−(−3,−2,3)=(1,−1,−1),
又因为⃗OE−⃗OA=⃗AE=λ⃗AB,
所以⃗OE=λ⃗AB+⃗OA=(λ,−λ,−λ)+(−3,−2,3)=(λ−3,−λ−2,−λ+3),
因为 , ,
⃗OE⊥⃗b ⃗b=(−2,3,2)
6
所以−2(λ−3)+3(−λ−2)+2(−λ+3)=0,解得λ= ,满足0≤λ≤1,
7
学科网(北京)股份有限公司所以⃗OE= (6 −3,− 6 −2,− 6 +3 ) = ( − 15 ,− 20 , 15) ,即E ( − 15 ,− 20 , 15) ,
7 7 7 7 7 7 7 7 7
( 15 20 15)
所以线段AB上存在一点E,使得⃗OE⊥⃗b,且E − ,− , .
7 7 7
【题型8 空间向量夹角余弦的坐标表示】
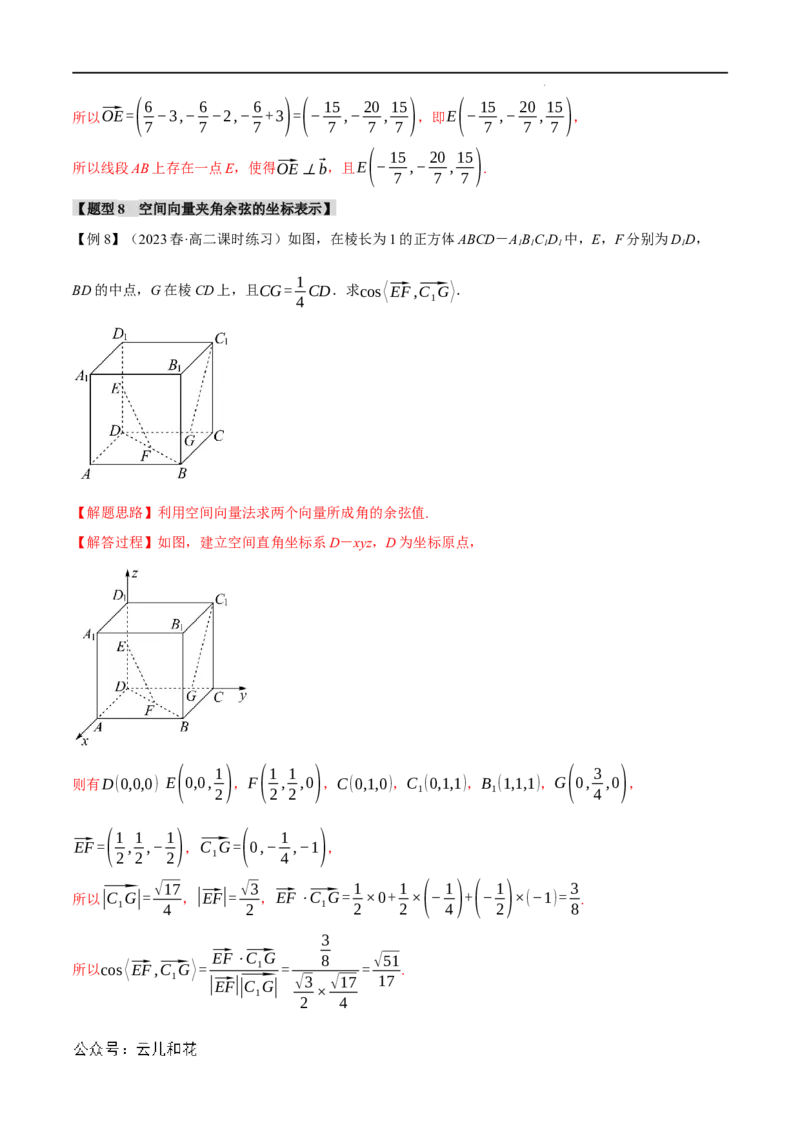
【例8】(2023春·高二课时练习)如图,在棱长为1的正方体ABCD-ABC D 中,E,F分别为DD,
1 1 1 1 1
1
BD的中点,G在棱CD上,且CG= CD.求cos⟨⃗EF,⃗C G⟩.
4 1
【解题思路】利用空间向量法求两个向量所成角的余弦值.
【解答过程】如图,建立空间直角坐标系D-xyz,D为坐标原点,
( 1) (1 1 ) ( 3 )
则有D(0,0,0) E 0,0, ,F , ,0 ,C(0,1,0),C (0,1,1),B (1,1,1),G 0, ,0 ,
2 2 2 1 1 4
⃗EF= (1 , 1 ,− 1) ,⃗C G= ( 0,− 1 ,−1 ) ,
2 2 2 1 4
所以 ⃗ |C G|= √17 ,|⃗EF|= √3 ,⃗EF⋅⃗C G= 1 ×0+ 1 × ( − 1) + ( − 1) ×(−1)= 3 .
1 4 2 1 2 2 4 2 8
3
⃗EF⋅⃗C G 8 √51
所以cos⟨⃗EF,⃗C G⟩= 1 = = .
1 |⃗EF|⃗
|C G|
√3 √17 17
×
1
2 4
学科网(北京)股份有限公司【变式8-1】(2023秋·河南周口·高二统考期末)已知向量⃗a=(−4,2,4),b=(−6,3,−2).
(1)求|a|;
(2)求向量⃑a与⃑b夹角的余弦值.
【解题思路】(1)由向量的模长坐标公式,可得答案;
(2)根据向量数量积的公式,结合模长公式,再由夹角公式,可得答案.
【解答过程】(1)因为 ,所以 .
a=(−4,2,4) |a|=√(−4) 2+22+42=√36=6
(2)因为a=(−4,2,4),b=(−6,3,−2),所以a⋅b=(−4,2,4)⋅(−6,3,−2)=24+6−8=22,
22 11
又因为|⃗a|=6,|b|=√(−6) 2+32+(−2) 2=7,所以cos⟨ ⃑a,⃗b⟩= = .
6×7 21
11
故⃑a与⃑b夹角的余弦值为 .
12
【变式8-2】(2023春·高二课时练习)已知空间中的三点P(−2,0,2),M(−1,1,2),N(−3,0,4),⃗a=⃗PM,
⃗b=⃗PN.
(1)求△PMN的面积;
(2)当k⃗a+⃗b与k⃗a−2⃗b的夹角为钝角时,求k的范围.
【解题思路】(1)应用向量坐标表示有 , ,由向量夹角的坐标运算可得
⃗a=(1,1,0) ⃗b=(−1,0,2)
√10
cos<⃗a,⃗b>=− ,再求其正弦值,应用三角形面积公式求面积;
10
(2)向量坐标表示得 , ,它们的夹角 为钝角,即 ,
k⃗a+⃗b=(k−1,k,2) k⃗a−2⃗b=(k+2,k,−4) θ cosθ<0
即可求参数范围,注意排除向量反向共线的情况.
【解答过程】(1)由题设 , ,则 ⃗a⋅⃗b −1 √10,
⃗a=(1,1,0) ⃗b=(−1,0,2) cos<⃗a,⃗b>= = =−
|⃗a||⃗b| √2×√5 10
√10 3√10
所以cos∠MPN=− ,故在△PMN中sin∠MPN= ,
10 10
1 3√10 3
故△PMN的面积为 ×√2×√5× = .
2 10 2
(2)由(1)知: , ,且它们夹角 为钝角,
k⃗a+⃗b=(k−1,k,2) k⃗a−2⃗b=(k+2,k,−4) θ
学科网(北京)股份有限公司所以
(k−1)(k+2)+k2−8
,即 ,
cosθ= <0 (k−1)(k+2)+k2−8<0
√(k−1) 2+k2+4⋅ √(k+2) 2+k2+16
5
所以2k2+k−10=(2k+5)(k−2)<0,可得− ;
1
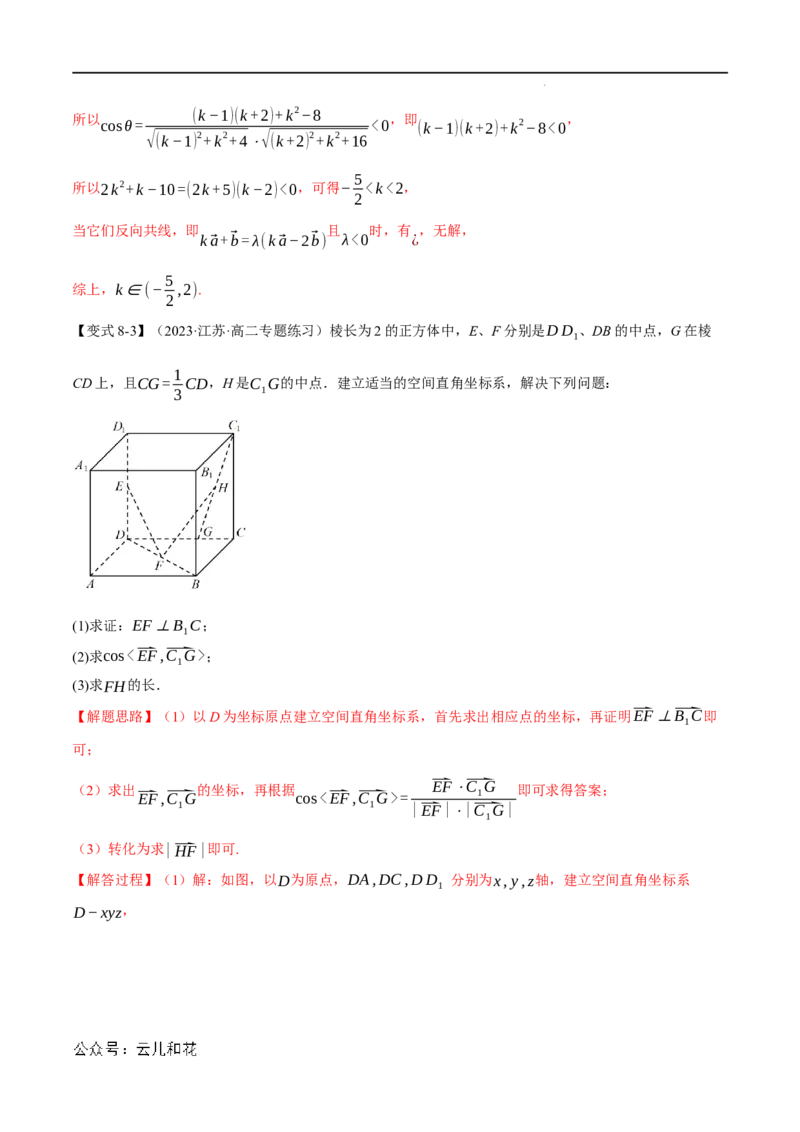
(3)求FH的长.
【解题思路】(1)以D为坐标原点建立空间直角坐标系,首先求出相应点的坐标,再证明⃑EF⊥⃑B C即
1
可;
(2)求出 的坐标,再根据 ⃑EF⋅⃑C G 即可求得答案;
⃑EF,⃑C G cos<⃑EF,⃑C G>= 1
1 1 |⃑EF|⋅|⃑C G|
1
(3)转化为求|⃑HF|即可.
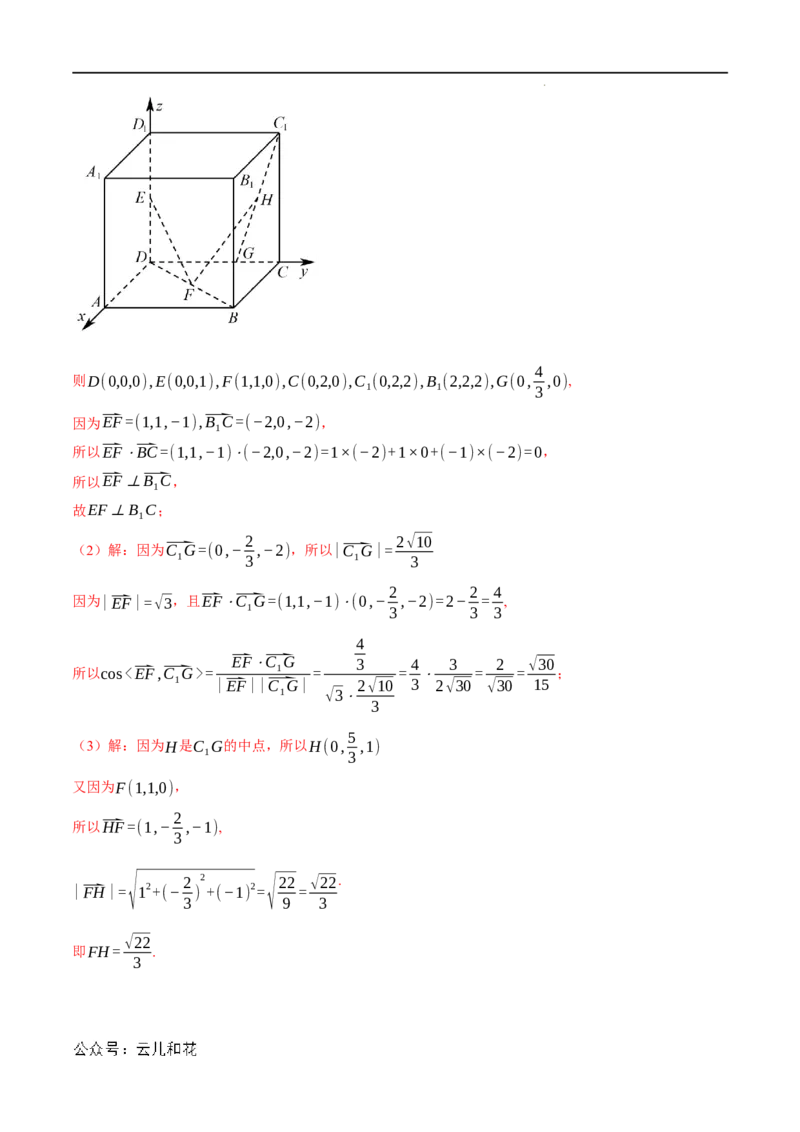
【解答过程】(1)解:如图,以D为原点,DA,DC,DD 分别为x,y,z轴,建立空间直角坐标系
1
D−xyz,
学科网(北京)股份有限公司4
则D(0,0,0),E(0,0,1),F(1,1,0),C(0,2,0),C (0,2,2),B (2,2,2),G(0, ,0),
1 1 3
因为⃑EF=(1,1,−1),⃑B C=(−2,0,−2),
1
所以⃑EF⋅⃑BC=(1,1,−1)⋅(−2,0,−2)=1×(−2)+1×0+(−1)×(−2)=0,
所以⃑EF⊥⃑B C,
1
故EF⊥B C;
1
2 2√10
(2)解:因为⃑C G=(0,− ,−2),所以|⃑C G|=
1 3 1 3
2 2 4
因为|⃑EF|=√3,且⃑EF⋅⃑C G=(1,1,−1)⋅(0,− ,−2)=2− = ,
1 3 3 3
4
⃑EF⋅⃑C G 3 4 3 2 √30
所以cos<⃑EF,⃑C G>= 1 = = ⋅ = = ;
1 |⃑EF||⃑C G| 2√10 3 2√30 √30 15
1 √3⋅
3
5
(3)解:因为H是C G的中点,所以H(0, ,1)
1 3
又因为F(1,1,0),
2
所以⃑HF=(1,− ,−1),
3
√ 2 2 √22 √22.
|⃑FH|= 12+(− ) +(−1) 2= =
3 9 3
√22
即FH= .
3
学科网(北京)股份有限公司