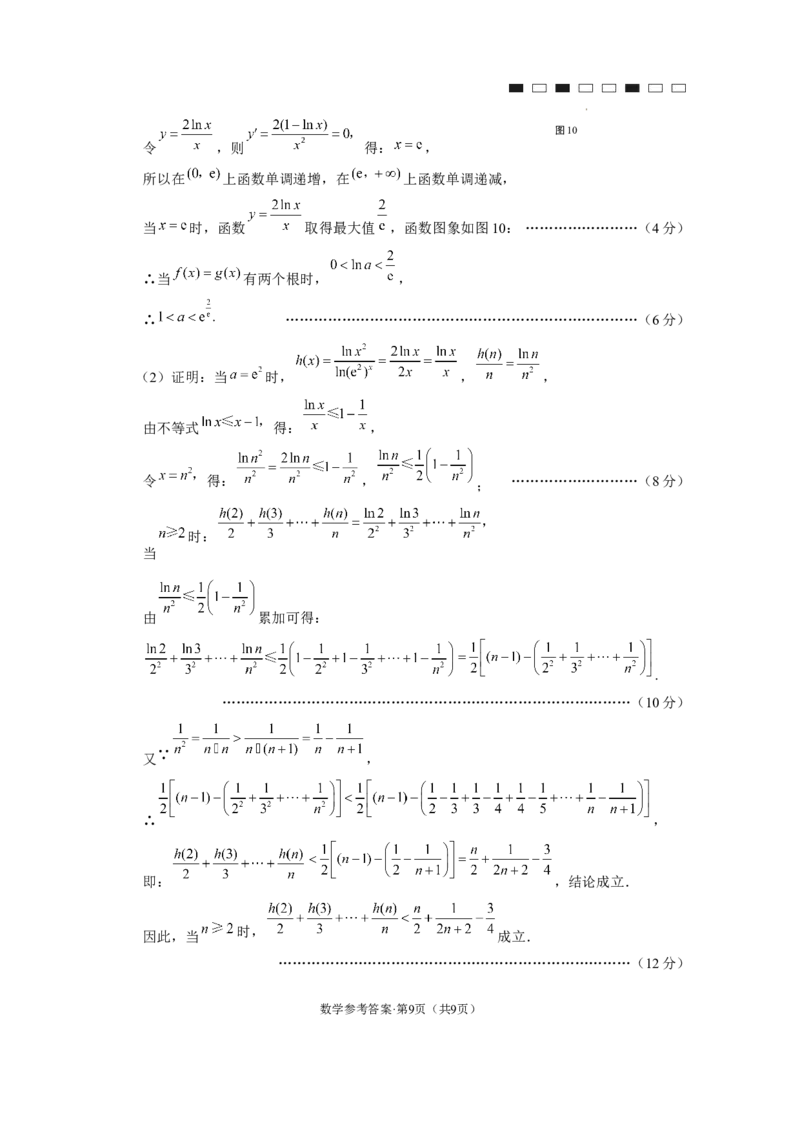文档内容
数学参考答案
一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只
有一项符合题目要求)
题号 1 2 3 4 5 6 7 8
答案 D C A C B D D A
【解析】
1.复数 则z的共轭复数 在复平面内对应的点 位于第一象限,
故选D.
3. 且向量 与 的夹角为
,
向量 在 上的投影为
,
又 ,
向量 在 上的投影向量为 ,故选A.
4.棱长为 的正方体的棱切球,其半径为面对角线的一半,即: ,所以该球的表面积
,故选C.
5.
,故选B.
6.记小明步行上班为事件 ,骑共享单车上班为事件 ,乘坐地铁上班为事件 ,小明上
班迟到为事件 .则 , , , ,
, , 所 以
,所以某天上班他迟到的概率是 ,故选D.
7.以 为直径的圆的方程为 ,若直线上存在一点 ,使得 ,则点
是在以 为直径的圆的内部.所以直线与圆相交. 即圆心 到直线 的距离
,所以 或 . 或 是“ ”成立的
数学参考答案·第1页(共9页)
学科网(北京)股份有限公司既不充分也不必要条件,故选D.
8.对于双曲线,原点到右支的最短距离为 ,所以在函数 上找一点 到原点的
最小值即为 .设点 ,则
所以当 时, ,所以实轴长为 ,故选A.
二、多项选择题(本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有
多项符合题目要求,全部选对的得5分,选对但不全的得2分,有选错的得0分)
题号 9 10 11 12
答案 BCD ABC ACD AD
【解析】
9.对于不等式 成立的条件之一是: 所以 :令 ,
,当 ,即 时取等号, 正确; :令 ,不
满足上述基本不等式的条件, 错误; :令 ,不满足上述基本
不等式的条件, 错误; : ,不满足上述基本不等式的条件
错误,故选BCD.
10.对于随机事件 , :若 为事件 的对立事件,由条件概率的性质可知:在事
件A的条件下,事件 发生和事件 发生的概率之和为1,所以 ,
正确; :若事件 互斥,则在事件 的条件下, 发生的概率等于在事件
的条件下, 发生的概率与 发生的概率之和.即 ,
正确; : , , 事件 独立, 正
确; :比如投掷一枚骰子,随机事件 为:向上的点数为奇数,则 ,随机事
件 为:向上的点数不小于4,则 ,
虽然 ,但事件 与事件 不
是对立事件, 错误,故选ABC.
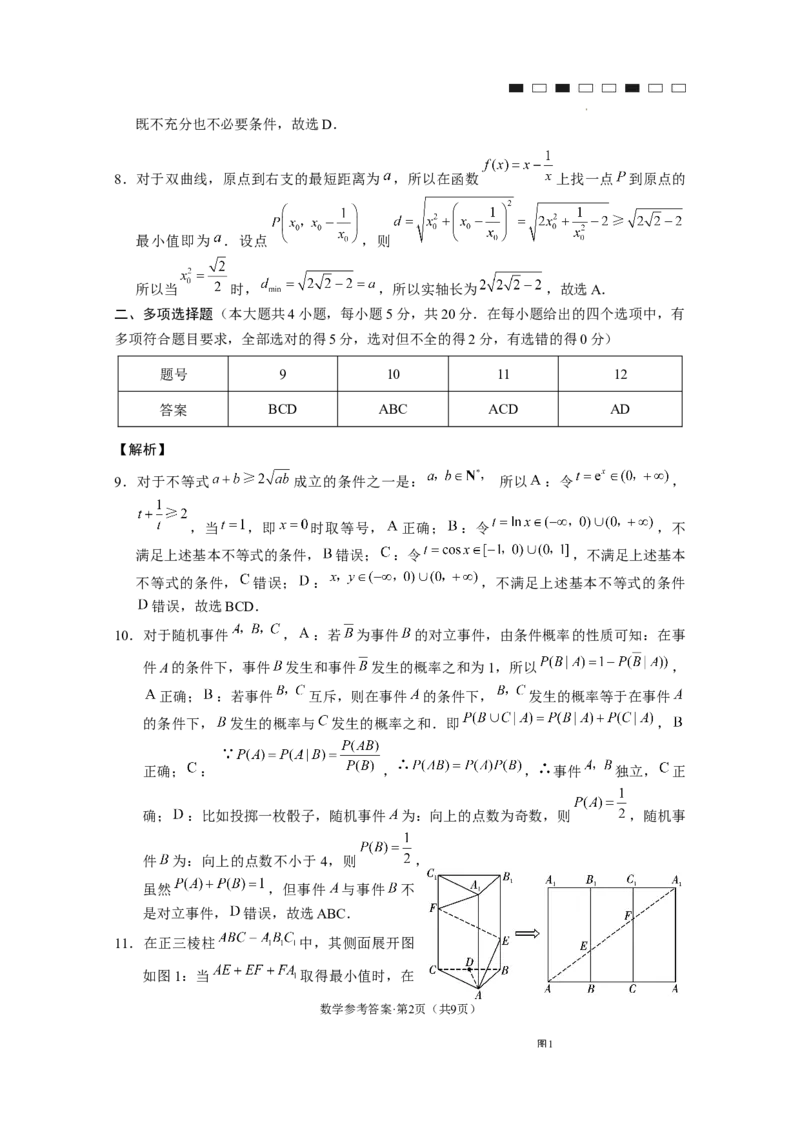
11.在正三棱柱 中,其侧面展开图
如图1:当 取得最小值时,在
数学参考答案·第2页(共9页)
学科网(北京)股份有限公司
图1侧面展开图中连接 ,分别为交 于点 ,由相似可知,
点 分别为 的三等分点, :如图2,过点 作
交 于 点 , 由 勾 股 定 理 得 : ,
, , ,∴ ,
正确; :由 选项知: ,所以 与平面 所成的角即
为 与平面 所成的角, ,∴ 为 与平面 所成的
角.又 且 为三等分点, , 错误;
:在正三棱柱 中, , . 又∵
且点 为中点,∴ . 又∵ , ,∴ ,
即直线 与 所成角为 , 正确; : , ,取
的中点 ,连接 ,则 , ,所以点 到平面 的距离等
于点 到平面 的距离,∴ , 正确,故选ACD.
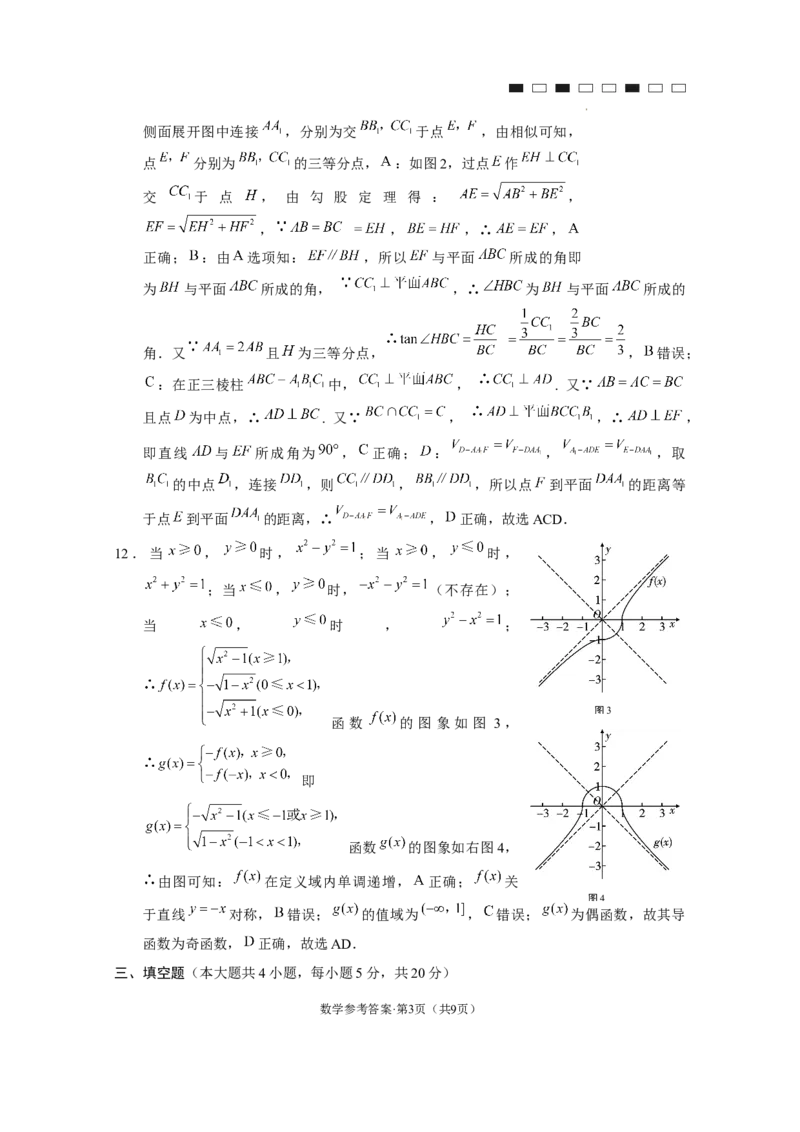
12.当 , 时, ;当 , 时,
;当 , 时, (不存在);
当 , 时 , ;
图3
函 数 的 图 象 如 图 3 ,
即
函数 的图象如右图4,
由图可知: 在定义域内单调递增, 正确; 关
图4
于直线 对称, 错误; 的值域为 , 错误; 为偶函数,故其导
函数为奇函数, 正确,故选AD.
三、填空题(本大题共4小题,每小题5分,共20分)
数学参考答案·第3页(共9页)
学科网(北京)股份有限公司题号 13 14 15 16
答案
【解析】
13. 展开式中的常数项是: .
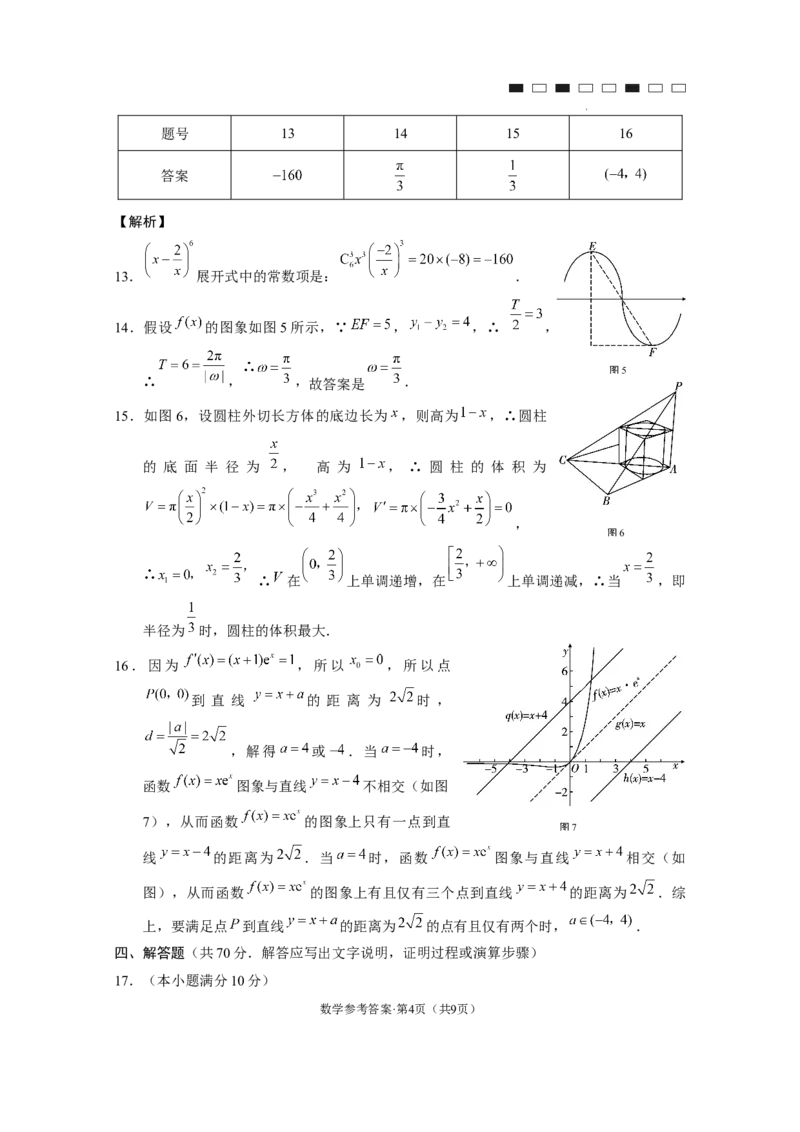
14.假设 的图象如图5所示,∵ , ,∴ ,
图5
∴ , ,故答案是 .
15.如图6,设圆柱外切长方体的底边长为 ,则高为 ,∴圆柱
的 底 面 半 径 为 , 高 为 , ∴ 圆 柱 的 体 积 为
,
图6
∴ 在 上单调递增,在 上单调递减,∴当 ,即
半径为 时,圆柱的体积最大.
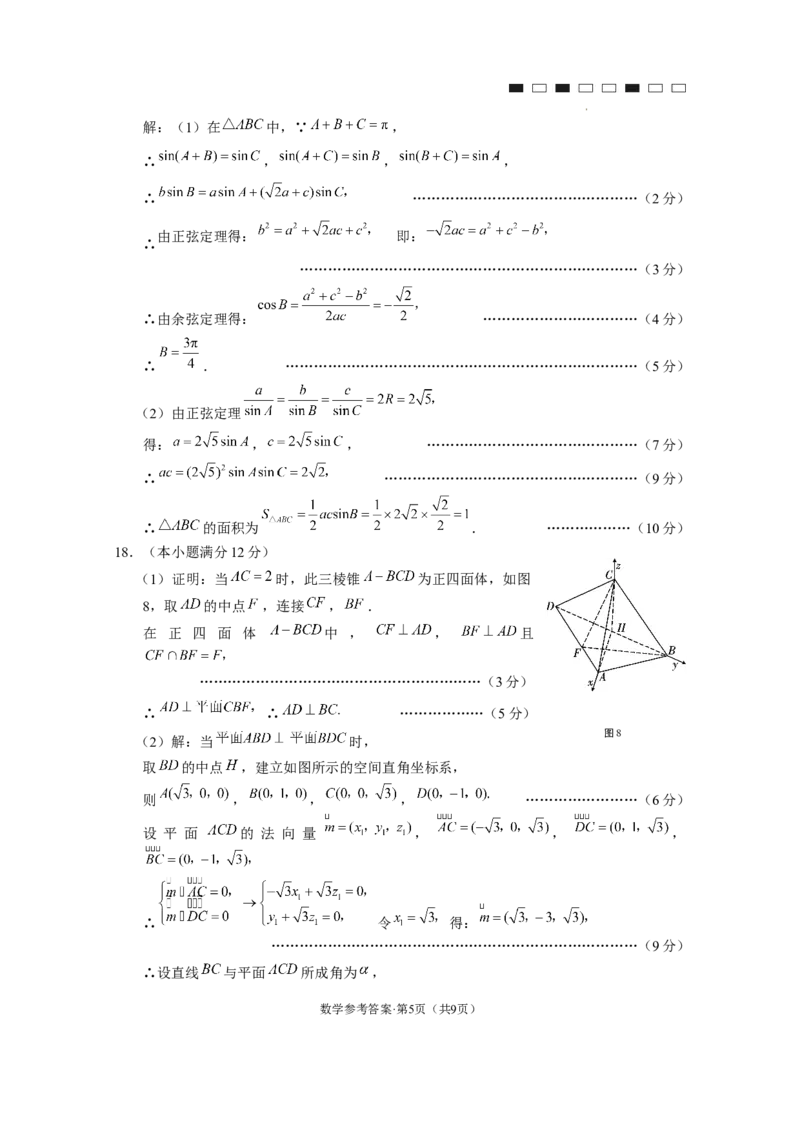
16.因为 ,所以 ,所以点
到 直 线 的 距 离 为 时 ,
,解得 或 .当 时,
函数 图象与直线 不相交(如图
7),从而函数 的图象上只有一点到直
图7
线 的距离为 .当 时,函数 图象与直线 相交(如
图),从而函数 的图象上有且仅有三个点到直线 的距离为 .综
上,要满足点 到直线 的距离为 的点有且仅有两个时, .
四、解答题(共70分.解答应写出文字说明,证明过程或演算步骤)
17.(本小题满分10分)
数学参考答案·第4页(共9页)
学科网(北京)股份有限公司解:(1)在 中,∵ ,
∴ , , ,
∴ …………………………………………(2分)
由正弦定理得: 即:
∴
………………………………………………………………(3分)
∴由余弦定理得: ……………………………(4分)
∴ . …………………………………………………………………(5分)
(2)由正弦定理
得: , , ………………………………………(7分)
∴ ………………………………………………(9分)
∴ 的面积为 . ………………(10分)
18.(本小题满分12分)
(1)证明:当 时,此三棱锥 为正四面体,如图
8,取 的中点 ,连接 , .
在 正 四 面 体 中 , , 且
……………………………………………………(3分)
∴ ∴ ………………(5分)
图8
(2)解:当 时,
取 的中点 ,建立如图所示的空间直角坐标系,
则 , , , ……………………(6分)
设 平 面 的 法 向 量 , , ,
∴ 令 得:
……………………………………………………………………(9分)
∴设直线 与平面 所成角为 ,
数学参考答案·第5页(共9页)
学科网(北京)股份有限公司则
∴
∴直线 与平面 所成角的余弦值为 . ………………………(12分)
19.(本小题满分12分)
解:(1)当小灯泡亮的时候,后一个元件A一定是合格的.在质检员犯错误的情况下,
对于前面的元件A,B分为两大类:
第一类:元件A合格,元件B不合格,故 ………………(2分)
第二类:元件B合格,元件A不合格,故 …………………(4分)
所以该质检员犯错误的概率为: …………………(5分)
甲中,记小灯泡亮的概率为 则
,
(2)在图
…………………………………………………………………(7分)
服从二项分布:
所以 ,
则
.
…………………………………………………………………(11分)
∴X的分布列为:
0 1 2 3
…………………………………………………………………………(
分)
20.(本小题满分12分)
数学参考答案·第6页(共9页)
学科网(北京)股份有限公司解:(1)当 时, ; …………………………………………………(2分)
时, ①,
当
②, ……………………………………………(4分)
①−②得:
∴ ,当 时, ,
∴ …………………………………………………………………(6分)
(2)∵
∴
………………………(8分)
∴ ①,
②,
又∵ ∴①+②得: …………………(10分)
∴ = …………………………………………………(12分)
21.(本小题满分12分)
(1)解:在椭圆 中,由题意可得: …………………(2分)
又∵ 的周长为 ,
∴由椭圆的定义可知: ,即
∴
图9
∴椭圆 的标准方程为 . ………………………(5分)
(2)证明:如图9,设: : , , ,
数学参考答案·第7页(共9页)
学科网(北京)股份有限公司联立方程: 得:
∴ , . ………………………………………(7分)
∵点 三点共线,
∴ ,即 ,
∴
∴
…………………………………………………………………(10分)
把 , 代入得:
∴ 三点共线. …………………………………………………(12分)
22.(本小题满分12分)
(1)解:当 时, ,
两 边 同 时 取 对 数 得 : , 即
,
∴ ……………………………(2
分)
数学参考答案·第8页(共9页)
学科网(北京)股份有限公司图10
令 ,则 得: ,
所以在 上函数单调递增,在 上函数单调递减,
当 时,函数 取得最大值 ,函数图象如图10: ……………………(4分)
∴当 有两个根时, ,
∴ …………………………………………………………………(6分)
(2)证明:当 时, , ,
由不等式 得: ,
令 得: ,
;
………………………(8分)
时:
当
由 累加可得:
.
……………………………………………………………………………(10分)
∵
又 ,
∴ ,
即: ,结论成立.
时,
因此,当 成立.
…………………………………………………………………(12分)
数学参考答案·第9页(共9页)
学科网(北京)股份有限公司数学参考答案·第10页(共9页)
学科网(北京)股份有限公司