文档内容
1
泸县普通高中共同体 2024 年秋期高二期中联合考试
数学试题
数学试卷分为第I卷(选择题)和第II卷(非选择题)两部分,共4页,满分150分.
注意事项:
1.答题前,考生务必将自己的姓名、班级、考号填写在答题卷上相应位置.
2.选择题答案使用2B铅笔填涂在答题卷对应题目号的位置上,填涂在试卷上无效.
3.非选择题答案请使用黑色签字笔填写在答题卷对应题目号的位置上,填写在试卷上无效.
第1卷(选择题共58分)
一、单选题:本题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只
有一项是符合题目要求的.
1. 某校为了解学生学习的情况,采用分层抽样的方法从高一240人、高二 200人、高三160人中,抽取60
人进行问卷调查,则高一年级被抽取的人数为
A. B. C. D.
2. 已知复数 满足 ,则复数 在复平面内的对应点位于()
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
3. 向量 在正方形网格中的位置如图所示.若向量 与 共线,则实数 ()
A. -2 B. -1 C. 1 D. 2
4. 已知空间中三点 ,则点 到直线 的距离为()
A B. C. D.
的
5. 空间中有两个不同 平面 和两条不同的直线 ,则下列说法中正确的是()
第1页1
A. 若 ,则 B. 若 ,则
C. 若 ,则 D. 若 ,则
6. 空气质量指数是评估空气质量状况的一组数字,空气质量指数划分为 、 、 、
、 和 六档,分别对应“优”、“良”、“轻度污染”、“中度污染”、“重度污染”
和“严重污染”六个等级.如图是某市2月1日至14日连续14天的空气质量指数趋势图,则下面说法中正
确的是().
A. 这14天中有5天空气质量为“中度污染”
B从2日到5日空气质量越来越好
C. 这14天中空气质量指数的中位数是214
D. 连续三天中空气质量指数方差最小是5日到7日
7. 三棱锥 中, 平面 , , , , ,则三棱锥
外接球的表面积为()
A. B. C. D.
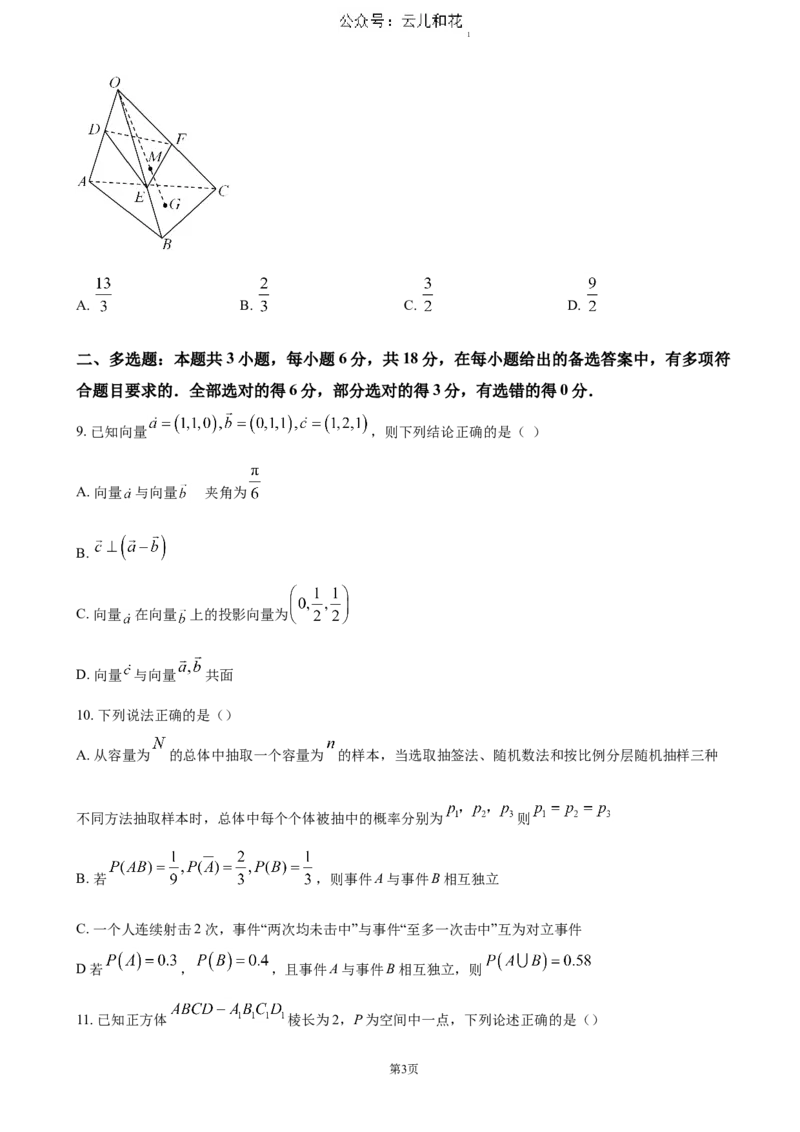
8. 如图,在三棱锥 中,点 为底面 的重心,点 是线段 上靠近点 的三等分点,
过点 的平面分别交棱 , , 于点 , , ,若 , , ,
则 ()
第2页1
A. B. C. D.
二、多选题:本题共3小题,每小题6分,共18分,在每小题给出的备选答案中,有多项符
合题目要求的.全部选对的得6分,部分选对的得3分,有选错的得0分.
9. 已知向量 ,则下列结论正确的是( )
A. 向量 与向量 的夹角为
B.
C. 向量 在向量 上的投影向量为
D. 向量 与向量 共面
10. 下列说法正确的是()
A. 从容量为 的总体中抽取一个容量为 的样本,当选取抽签法、随机数法和按比例分层随机抽样三种
不同方法抽取样本时,总体中每个个体被抽中的概率分别为 则
B. 若 ,则事件A与事件B相互独立
C. 一个人连续射击2次,事件“两次均未击中”与事件“至多一次击中”互为对立事件
D若 , ,且事件A与事件B相互独立,则
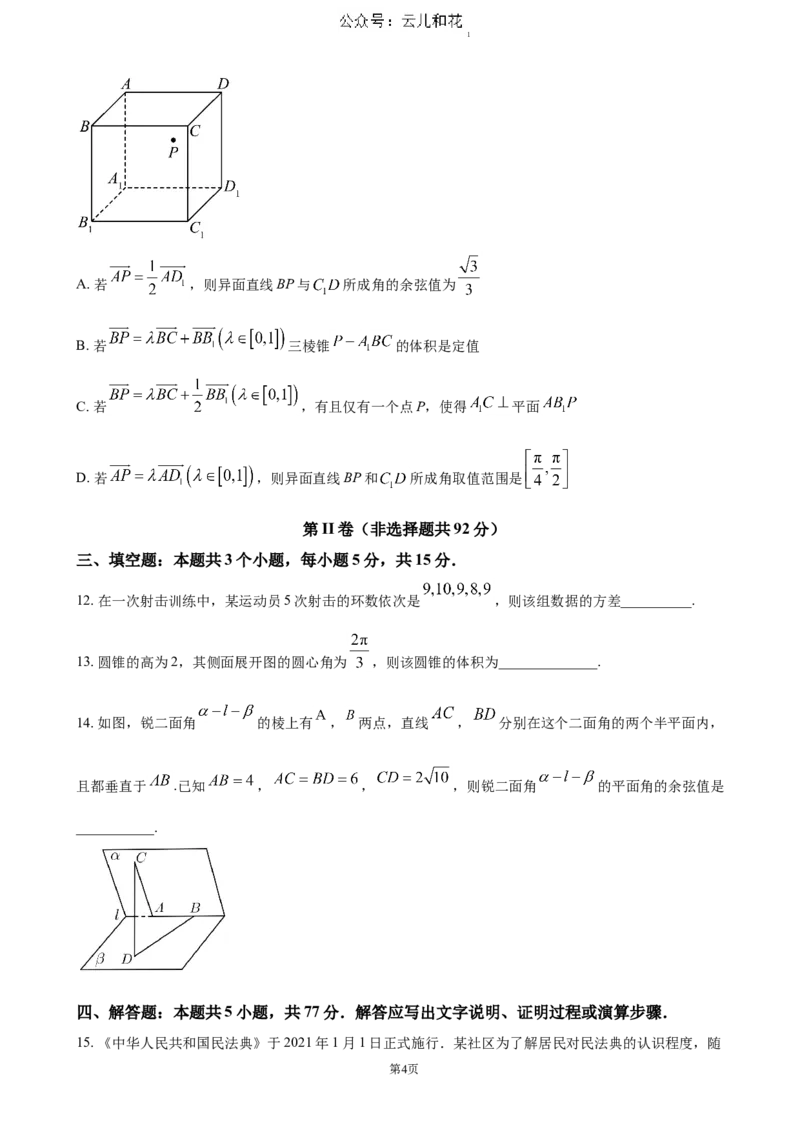
11. 已知正方体 棱长为2,P为空间中一点,下列论述正确的是()
第3页1
A. 若 ,则异面直线BP与 所成角的余弦值为
B. 若 三棱锥 的体积是定值
C. 若 ,有且仅有一个点P,使得 平面
D. 若 ,则异面直线BP和 所成角取值范围是
第II卷(非选择题共92分)
三、填空题:本题共3个小题,每小题5分,共15分.
12. 在一次射击训练中,某运动员5次射击的环数依次是 ,则该组数据的方差__________.
13. 圆锥的高为2,其侧面展开图的圆心角为 ,则该圆锥的体积为______________.
14. 如图,锐二面角 的棱上有 , 两点,直线 , 分别在这个二面角的两个半平面内,
且都垂直于 .已知 , , ,则锐二面角 的平面角的余弦值是
___________.
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15. 《中华人民共和国民法典》于2021年1月1日正式施行.某社区为了解居民对民法典的认识程度,随
第4页1
机抽取了一定数量的居民进行问卷测试(满分:100分),并根据测试成绩绘制了如图所示的频率分布直
方图.
(1)估计该组测试成绩的平均数和第57百分位数;
(2)该社区在参加问卷且测试成绩位于区间 和 的居民中,采用分层随机抽样,确定了5
人.若从这5人中随机抽取2人作为该社区民法典宣讲员,设事件 “两人的测试成绩分别位于 和
”,求 .
16. 记 的内角 , , 所对的边分别为 ,已知 .
(1)求 ;
(2)若 是 的中线,且 , 的面积为 ,求 的周长.
17. 某足球俱乐部举办新一届足球赛,按比赛规则,进入淘汰赛的两支球队如果在 120分钟内未分出
胜负,则需进行点球大战.点球大战规则如下:第一阶段,双方各派5名球员轮流罚球,双方各罚一
球为一轮,球员每罚进一球则为本方获得1分,未罚进不得分,当分差拉大到即使落后一方剩下的球
员全部罚进也不能追上的时候,比赛即宣告结束,剩下的球员无需出场罚球.若5名球员全部罚球后
双方得分一样,则进入第二阶段的比赛.设甲、乙两支球队进入点球大战,由甲队球员先罚球,甲队
每位球员罚进点球的概率均为 ,乙队每位球员罚进点球的概率均为 .假设每轮罚球中,两队进球
与否互不影响,各轮结果也互不影响.
(1)求每一轮罚球中,甲、乙两队打成平局的概率;
(2)若在点球大战的第一阶段,甲队前两名球员均得分而乙队前两名球员均未得分,甲队暂时以 领
第5页1
先,求甲队第5个球员需出场罚球的概率.
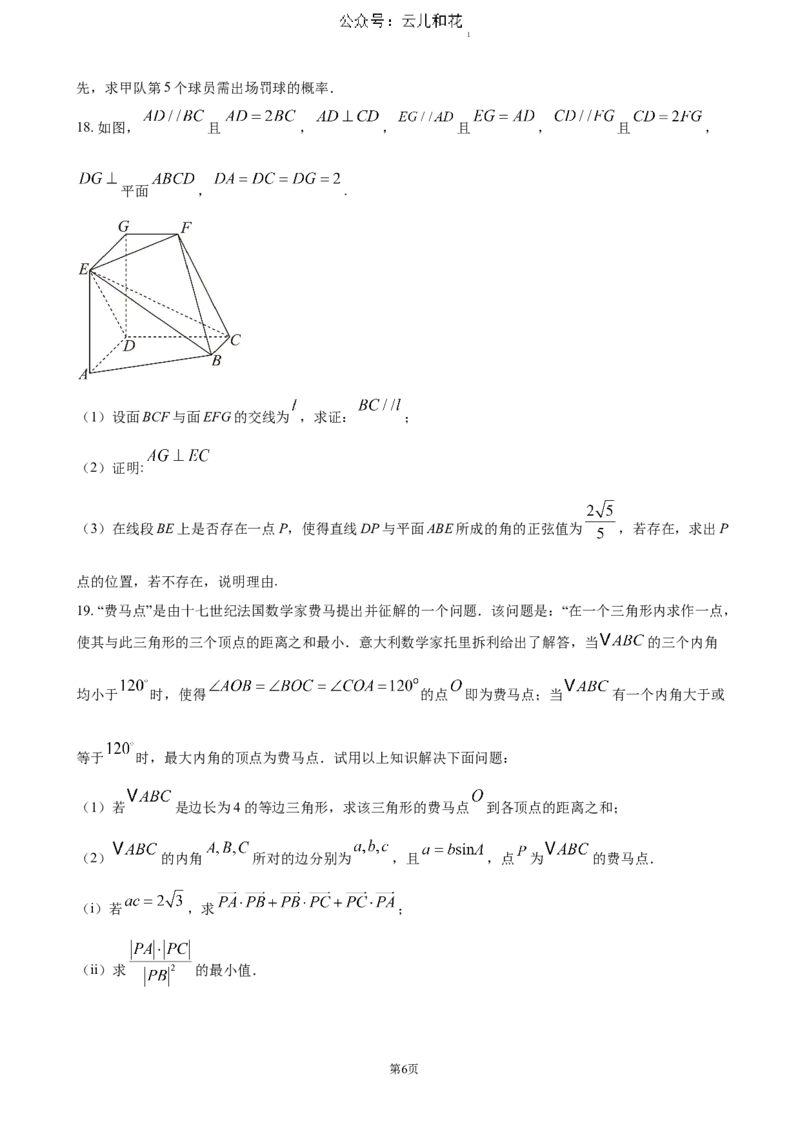
18. 如图, 且 , , 且 , 且 ,
平面 , .
(1)设面BCF与面EFG的交线为 ,求证: ;
(2)证明:
(3)在线段BE上是否存在一点P,使得直线DP与平面ABE所成的角的正弦值为 ,若存在,求出P
点的位置,若不存在,说明理由.
19. “费马点”是由十七世纪法国数学家费马提出并征解的一个问题.该问题是:“在一个三角形内求作一点,
使其与此三角形的三个顶点的距离之和最小.意大利数学家托里拆利给出了解答,当 的三个内角
均小于 时,使得 的点 即为费马点;当 有一个内角大于或
等于 时,最大内角的顶点为费马点.试用以上知识解决下面问题:
(1)若 是边长为4的等边三角形,求该三角形的费马点 到各顶点的距离之和;
(2) 的内角 所对的边分别为 ,且 ,点 为 的费马点.
(i)若 ,求 ;
(ii)求 的最小值.
第6页1
泸县普通高中共同体 2024 年秋期高二期中联合考试
数学试题
一、单选题:本题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只
有一项是符合题目要求的.
1.
【答案】B
2.
【答案】B
3.
【答案】D
4.
【答案】C
5.
【答案】A
6.
【答案】B
7.
【答案】B
8.
【答案】D
二、多选题:本题共3小题,每小题6分,共18分,在每小题给出的备选答案中,有多项符
合题目要求的.全部选对的得6分,部分选对的得3分,有选错的得0分.
9.
【答案】BCD
10.
【答案】ABD
11.
【答案】BD
第II卷(非选择题共92分)
三、填空题:本题共3个小题,每小题5分,共15分.
第7页1
12.
【答案】 ##
13.
【答案】
14.
【答案】
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.
【解析】
【分析】(1)利用频率分布直方图计算平均数及百分位数;
(2)根据分层抽样确定测试成绩分别位于 和 的人数,按照古典概型计算即可.
【
小问1详解】
由频率分布直方图可知测试成绩的平均数
.
测试成绩落在区间 的频率为 ,
落在区间 的频率为 ,
所以设第57百分位数为a,有 ,
解得 ;
【小问2详解】
由题知,测试分数位于区间 、 的人数之比为 ,
所以采用分层随机抽样确定的5人,在区间 中3人,用 , , 表示,在区间 中2
第8页1
人,用 , 表示,
从这5人中抽取2人的所有可能情况有:
, , , , , , , , ,
,共10种,
其中“分别落在区间 和 ”有6种,
所以 .
16.
【解析】
【分析】(1)由正弦定理、三角形内角和定理及三角恒等变换求角 ;
(2)由三角形的面积公式得 的值,再由向量的线性运算及向量的模求 的值,最后由余弦定理求
的值.
【
小问1详解】
∵ ,
∴由正弦定理得 ,
∴ ,
∴ ,
∵ ,
∴ .即 ,
∵ ,∴ .
第9页1
∴ ,即 .
【小问2详解】
∵由题意得 ,
∴ .
∵ 是 的中线,
∴ ,
∴ ,
∴ , ,
由余弦定理得 ,
∴ .
∴ 的周长为 .
17.
【解析】
【分析】(1)根据平局的概念,列举出所包含的情况,利用概率的乘法公式,可得答案;
(2)根据第一阶段的规则,列举出符合题意的比分,利用概率的乘法公式以及加法公式,可得答案.
【小问1详解】
每一轮出现平局的情况包括:事件 {甲乙两队都进球}和事件 {甲乙两队都不进},
, , ,
所以每一轮罚球中,甲、乙两队打成平局的概率为 .
第10页1
【小问2详解】
在第三轮比完之后,甲乙两队分差小于三分,就必须要进行第四轮,
第三轮符合题意的情况包括:事件 {甲乙的比分为 }、事件 {甲乙的比分为 }、事件
{甲乙的比分为 },
则 , , ;
在第四轮比完之后,甲乙两队分差小于两分,就必须进行第五轮,
在事件 发生的条件下,第四轮过后符合题意的情况有事件 {甲乙的比分为 },
则 ;
在事件 发生的条件下,第四轮过后符合题意的情况有事件 {甲乙的比分为 },
则 ;
在事件 发生的条件下,第四轮过后符合题意的情况有事件 {甲乙的比分为 }、事件 {甲乙
的比分为 }、事件 {甲乙的比分为 },
则 , , ;
综上所述,甲队暂时以 领先,甲队第5个球员需出场罚球的概率
.
18.
【解析】
【分析】(1)由线面平行的判定定理和性质定理证明即可;
(2)由线面垂直的判定定理和性质定理证明即可;
(3)则以D为原点,建立空间直角坐标系,先求出 点坐标,直线DP的方向向量与平面ABE的法向量,
第11页1
由线面角的向量公式代入即可得出答案.
【小问1详解】
因为 , ,所以 ,
又 平面 , 平面 ,
所以 面 ,又 平面 ,平面 平面 ,
所以 .
【小问2详解】
因为 且 ,所以四边形ADGE为平行四边形,
又 ,所以四边形ADGE为菱形,所以AG⊥DE.
因为 平面 , 平面 ,所以 ,
又 , 平面 ,所以CD⊥面 ,
又 面 ,所以 ,又 ,
平面 ,所以 面 ,又 面 ,
所以 .
【小问3详解】
由于 , , , 平面 , ,
则以D为原点,分别以 , , 的方向为x轴,y轴,z轴的正方向的空间直角坐标系,如图,
第12页1
于是 , ,设平面ABE的法向量为 ,
则 , ,令 ,得 ,
假设线段BE上存在点P,使得直线DP与平面ABE所成 的角的正弦值为 .
设 , ,
,
解得: .
所以线段BE上存在点P,且 时,使得直线DP与平面ABE所成的角的正弦值为 .
19.
【解析】
【分析】(1)过 作 于 ,结合题意即可求解;
(2)(i)根据正弦定理求得 ,由三角形面积公式及向量数量积即可求解;( ii)设
,得出 ,由勾股定理得
出 ,根据基本不等式求解范围即可.
【小问1详解】
因为 为等边三角形,三个内角均小于 ,故费马点 在三角形内,满足
,且 ,如图:
第13页1
过 作 于 ,则 ,故 ,
所以该三角形的费马点 到各顶点的距离之和为 .
【小问2详解】
(i)因为 ,由正弦定理 ,且 ,
所以 得 ,
所以 的三个角都小于 ,
则由费马点定义可知, ,
设 , ,
由 得: ,
整理得 ,
则
.
(ii)由(i)知 ,所以点 在 内部,且 ,
第14页1
设 ,
所以 ,
由余弦定理得, ,
,
,
由勾股定理得, ,即 ,
所以 ,即 ,
而 ,
当且仅当 ,即 时,等号成立.
设 ,则 ,解得 或 (舍去),
由 ,
故 ,最小值为 .
第15页1
第16页