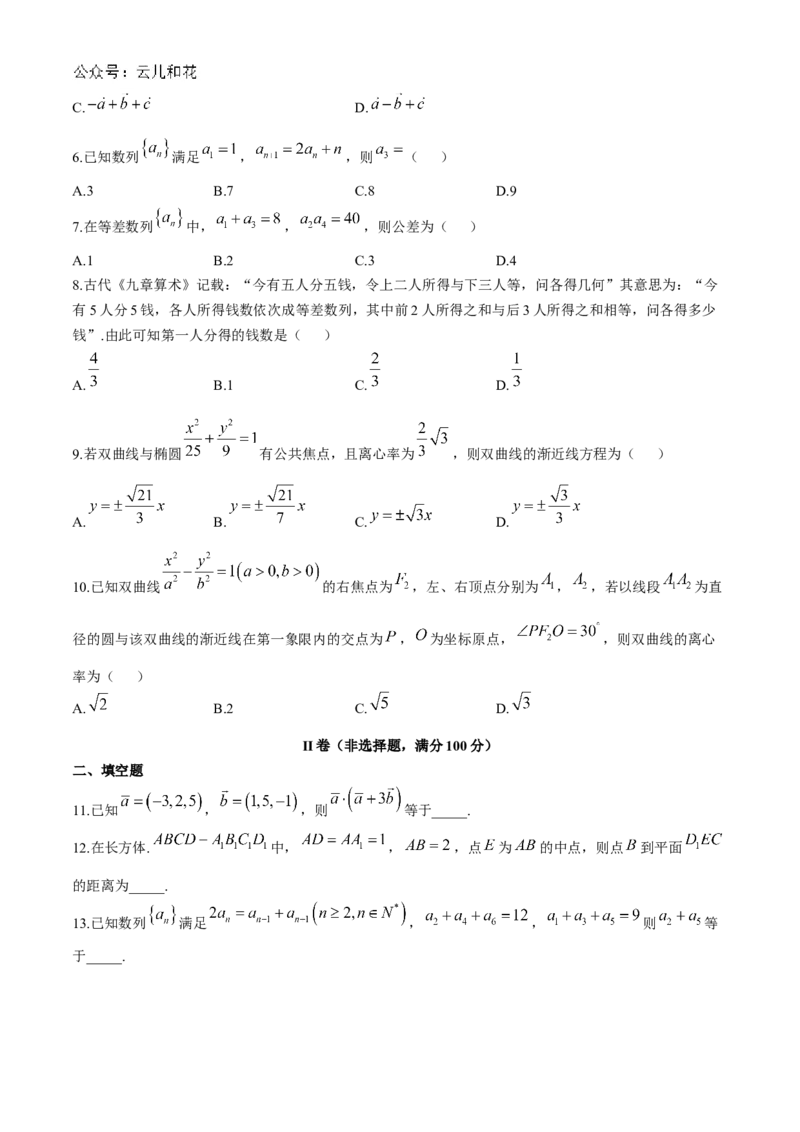文档内容
2024-2025 学年度高二年级第一学期联合考试
数学试卷
注意事项:
1、本试卷分第I卷(选择题)和第II卷(非选择题)两部分.满分150分,考试时间120分钟.
2、答I卷前,考生务必将自己的姓名、准考证号、考试科目涂写在答题卡上,只交答题卡,
试卷学生带走,以备讲评。
第I卷(选择题,满分50分)
一、选择题(本题共10小题,每小题只有一个选项符合要求。每题5分,共50分)
1.直线 的倾斜角是( )
A. B. C. D.
2.已知直线 ,与 平行,则 的值是( )
A.0或1 B.1或 C.0或 D.
3.圆 在点 处的切线方程为( ).
A. B.
C. D.
4.抛物线 过点 ,则 的准线方程为( )
A. B. C. D.
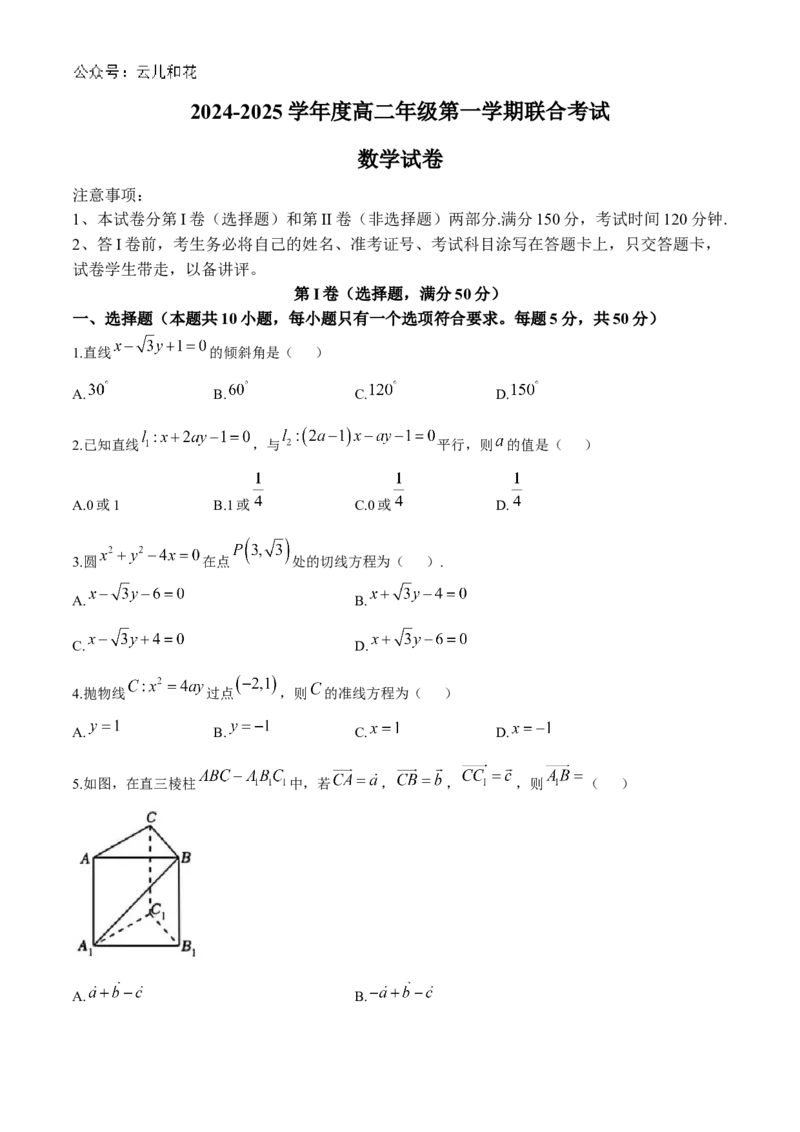
5.如图,在直三棱柱 中,若 , , ,则 ( )
A. B.C. D.
6.已知数列 满足 , ,则 ( )
A.3 B.7 C.8 D.9
7.在等差数列 中, , ,则公差为( )
A.1 B.2 C.3 D.4
8.古代《九章算术》记载:“今有五人分五钱,令上二人所得与下三人等,问各得几何”其意思为:“今
有5人分5钱,各人所得钱数依次成等差数列,其中前2人所得之和与后3人所得之和相等,问各得多少
钱”.由此可知第一人分得的钱数是( )
A. B.1 C. D.
9.若双曲线与椭圆 有公共焦点,且离心率为 ,则双曲线的渐近线方程为( )
A. B. C. D.
10.已知双曲线 的右焦点为 ,左、右顶点分别为 , ,若以线段 为直
径的圆与该双曲线的渐近线在第一象限内的交点为 , 为坐标原点, ,则双曲线的离心
率为( )
A. B.2 C. D.
II卷(非选择题,满分100分)
二、填空题
11.已知 , ,则 等于_____.
12.在长方体. 中, , ,点 为 的中点,则点 到平面
的距离为_____.
13.已知数列 满足 , , 则 等
于_____.14.已知圆 与圆 相交于点A、B.①若 ,则公共弦所在
直线方程为_____;②若弦长 ,则 _____.
15.已知抛物线C: 的焦点为F,直线1与抛物线C交于A、B两点,若AB的中点的纵坐标为5,
则 _____.
三、解答题
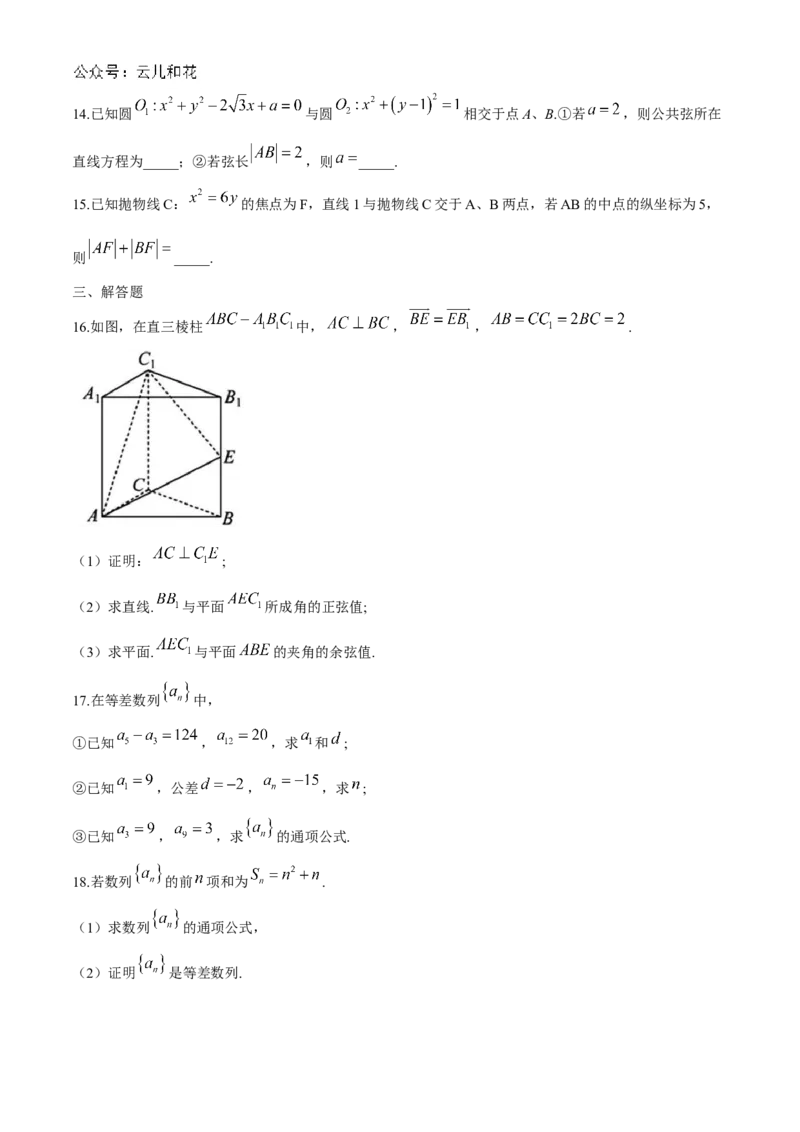
16.如图,在直三棱柱 中, , , .
(1)证明: ;
(2)求直线. 与平面 所成角的正弦值;
(3)求平面. 与平面 的夹角的余弦值.
17.在等差数列 中,
①已知 , ,求 和 ;
②已知 ,公差 , ,求 ;
③已知 , ,求 的通项公式.
18.若数列 的前 项和为 .
(1)求数列 的通项公式,
(2)证明 是等差数列.19.已知椭圆的焦点在 轴上,一个顶点为 ,离心率 ,过椭圆的右焦点 的直线1与坐标轴
不垂直,且交椭圆于 , 两点
(1)求椭圆的标准方程
(2)当直线1的斜率为 时,求弦长 的值.
20.已知椭圆 过点 ,且离心率为 .
(1)求椭圆C的标准方程;
(2)过椭圆 的右焦点 的直线 与椭圆相交于 , 两点,且 ,求直线 的方程.2024-2025 学年度高二年级第一学期联合考试
数学答案与评分标准参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 A C D B B C C A D B
11.44
12.
13.7
14. -2
15.13
16.(1)证明见解析
(2)
(3)
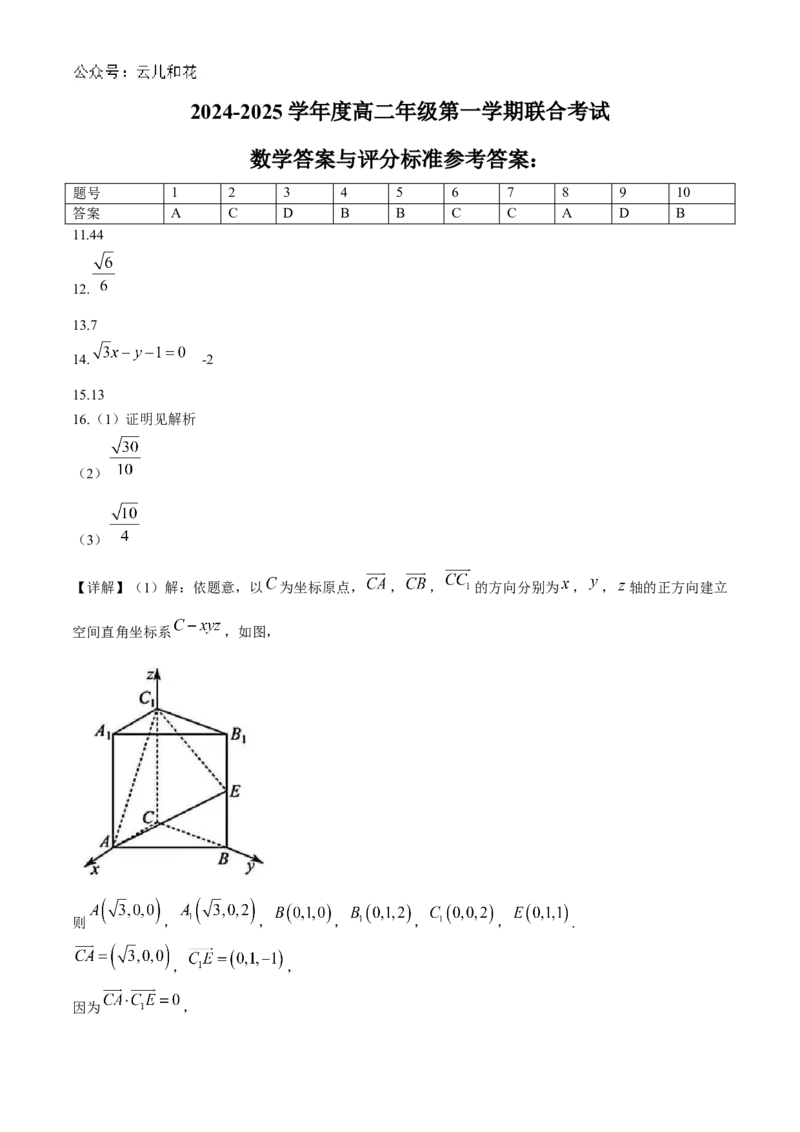
【详解】(1)解:依题意,以 为坐标原点, , , 的方向分别为 , , 轴的正方向建立
空间直角坐标系 ,如图,
则 , , , , , .
, ,
因为 ,所以 .
(2)解:结合(1)得 , , ,
设平面 的法向量为 ,
则
令 ,得 .
设直线 与平面 所成角为 ,
则 ,
所以直线 与平面 所成角的正弦值为 .
(3)解:结合(1) ,
设平面 的法向量为 ,
则
令 ,则 ,
由(2)知平面 的法向量为
设平面 和平面 的夹角为 ,
则 .
所以,平面 与平面 的夹角余弦值为 .
17.(1)① , .②
③ .
【详解】(1)因为 ,所以公差 .
由 ,所以 ,
故 , .
(2)由 , ,公差 , ,得 ,
解得 .
(3)由已知可得 ,解得
所以 .
18.(1)
(2)证明略
19.(1) (2)
【详解】(1)依题意设椭圆的标准方程为 ,
则 , ,所以 ,解得 ,
所以椭圆的标准方程为 .
(2)由(1)知 ,则直线 ,联立 ,消去 并整理得 ,
设 , ,
则 , ,
所以 .
20.(1)
(2)
【详解】(1)由椭圆过点 可知, ,
又 得 ,即 ,
所以 ,所以 ,
所以椭圆 的标准方程为 .
(2)由(1)知, ,设直线 的方程为 ,
, 联立 ,
解得 ,
所以 , ,
由 得 ,即 ,所以 ,所以 , ,
所以 ,化简得 ,
所以 ,所以直线 的方程