文档内容
秘密★考试结束前
丽江市2025届高中毕业生复习统一检测
数学试卷
(全卷四个大题,共19个小题,共6页;满分150分,考试用时120分钟)
注意事项:
1.本卷为试题卷。考生必须在答题卡上解题作答。答案应书写在答题卡的相应位置上,在
试题卷、草稿纸上作答无效。
2.考试结束后,请将答题卡交回。
一、单项选择题(本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,
只有一项符合题目要求)
1.若复数z满足 (i为虚数单位),则z的模 ( )
A. B.1 C. D.5
2.已知集合 , ,则 ( )
A. B. C. D.
3.已知向量 , 满足 , ,且 ,则 ( )
A. B. C.1 D.2
4.“ ”是“方程 表示椭圆”的( )
A.既不充分也不必要条件 B.充分不必要条件
C.必要不充分条件 D.充要条件
5.已知函数 ,则下列函数是奇函数的是( )
A. B.
数学试卷·第1页(共6页)
学科网(北京)股份有限公司C. D.
6.已知 ,则 ( )
A. B. C. D.
7.某同学掷一枚正方体骰子5次,记录每次骰子出现的点数,统计出结果的平均数为 2,
方差为0.4,可判断这组数据的众数为( )
A.1 B.2 C.3 D.4
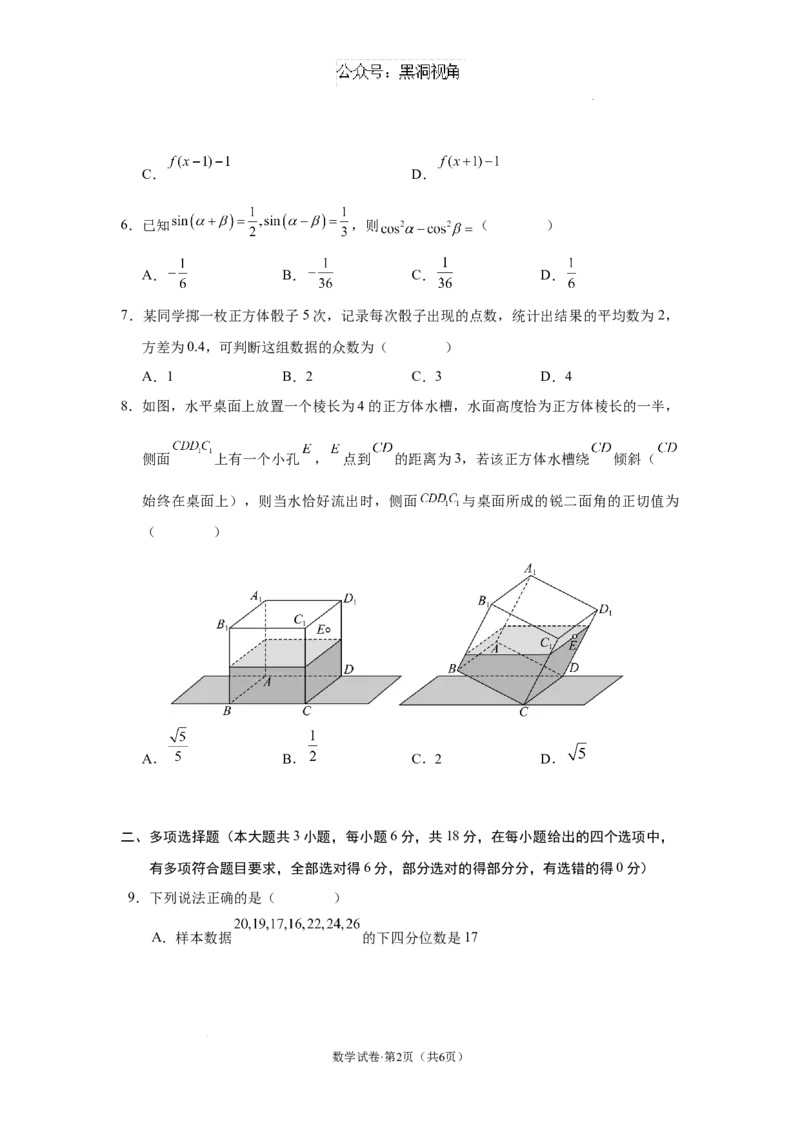
8.如图,水平桌面上放置一个棱长为4的正方体水槽,水面高度恰为正方体棱长的一半,
侧面 上有一个小孔 , 点到 的距离为3,若该正方体水槽绕 倾斜(
始终在桌面上),则当水恰好流出时,侧面 与桌面所成的锐二面角的正切值为
( )
A. B. C.2 D.
二、多项选择题(本大题共3小题,每小题6分,共18分,在每小题给出的四个选项中,
有多项符合题目要求,全部选对得6分,部分选对的得部分分,有选错的得0分)
9.下列说法正确的是( )
A.样本数据 的下四分位数是17
数学试卷·第2页(共6页)
学科网(北京)股份有限公司B.在比例分配的分层随机抽样中,若第一层的样本量为10,平均值为9,第二层的
样
本量为20,平均值为12,则所抽样本的平均值为11
C.若随机变量 ,则
D.若随机变量 ,若 ,则
10.已知函数 ,则( )
A.函数 的最小正周期为
B.直线 是函数 的图象的一条对称轴
C.若 时, 恒成立,则实数m的取值范围为
D.将函数 的图象上的所有点的横坐标缩小为原来的 ,再将所得的图象向右平
移 个单位,得到函数 的图象,若 时,函数 有且仅有5个零点,
则实数t的取值范围为 13 4
,
12 3
11.已知点 是左、右焦点为 , 的椭圆 : 上的动点,则( )
A.若 ,则 的面积为
B.使 为直角三角形的点 有6个
C. 的最大值为
数学试卷·第3页(共6页)
学科网(北京)股份有限公司D.若 ,则 的最大、最小值分别为 和
三、填空题(本大题共3小题,每小题5分,共15分)
12.在 中内角 所对的边分别为 ,且 , , ,则
.
13. 的展开式中 的系数为 (用数字作答).
14.已知不等式 对任意 恒成立,则实数 的取值范
围为 .
四、解答题(本大题共5小题,共77分,解答应写出文字说明,证明过程或演算步骤)
15.(本小题满分13分)
已知函数 .
(1)求曲线 在 处的切线方程;
(2)若 ,求函数 在 上的最值.
数学试卷·第4页(共6页)
学科网(北京)股份有限公司16.(本小题满分15分)
已知数列 的首项 ,且满足 .
(1)求证:数列 为等比数列.
(2)若 求满足条件的最大整数n.
17.(本小题满分15分)
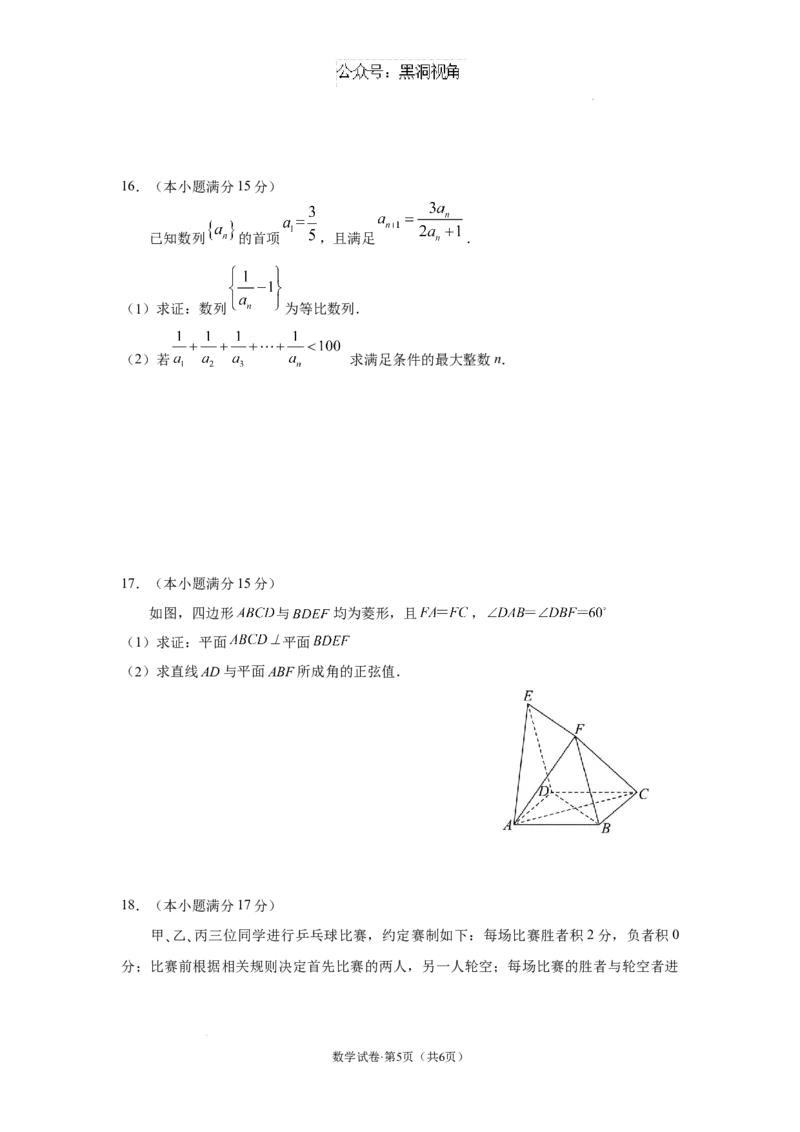
如图,四边形 与 均为菱形,且 ,
(1)求证:平面 平面
(2)求直线AD与平面ABF所成角的正弦值.
18.(本小题满分17分)
甲、乙、丙三位同学进行乒乓球比赛,约定赛制如下:每场比赛胜者积2分,负者积0
分;比赛前根据相关规则决定首先比赛的两人,另一人轮空;每场比赛的胜者与轮空者进
数学试卷·第5页(共6页)
学科网(北京)股份有限公司行下一场比赛,负者下一场轮空;积分首先累计到4分者获得比赛胜利,比赛结束. 已知
甲与乙比赛时,甲获胜的概率为 ,甲与丙比赛时,甲获胜的概率为 ,乙与丙比赛时,
乙获胜的概率为 .
(1)若 ,求比赛结束时,三人总积分 的分布列与期望;
(2)若 ,假设乙获得了指定首次比赛选手的权利,为获得比赛的胜利,试分析
乙
的最优指定策略.
19.(本小题满分17分)
已知双曲线 的两条渐近线方程为 为 上
一点.
(1)求双曲线 的方程;
(2)若过点 的直线 与 仅有1个公共点,求 的方程;
(3)过双曲线 的右焦点 作两条互相垂直的直线 , ,且 与 交于 两点,
记 的中点 与 交于 两点,记 的中点为 .若 ,求点
到直线 的距离的最大值.
数学试卷·第6页(共6页)
学科网(北京)股份有限公司