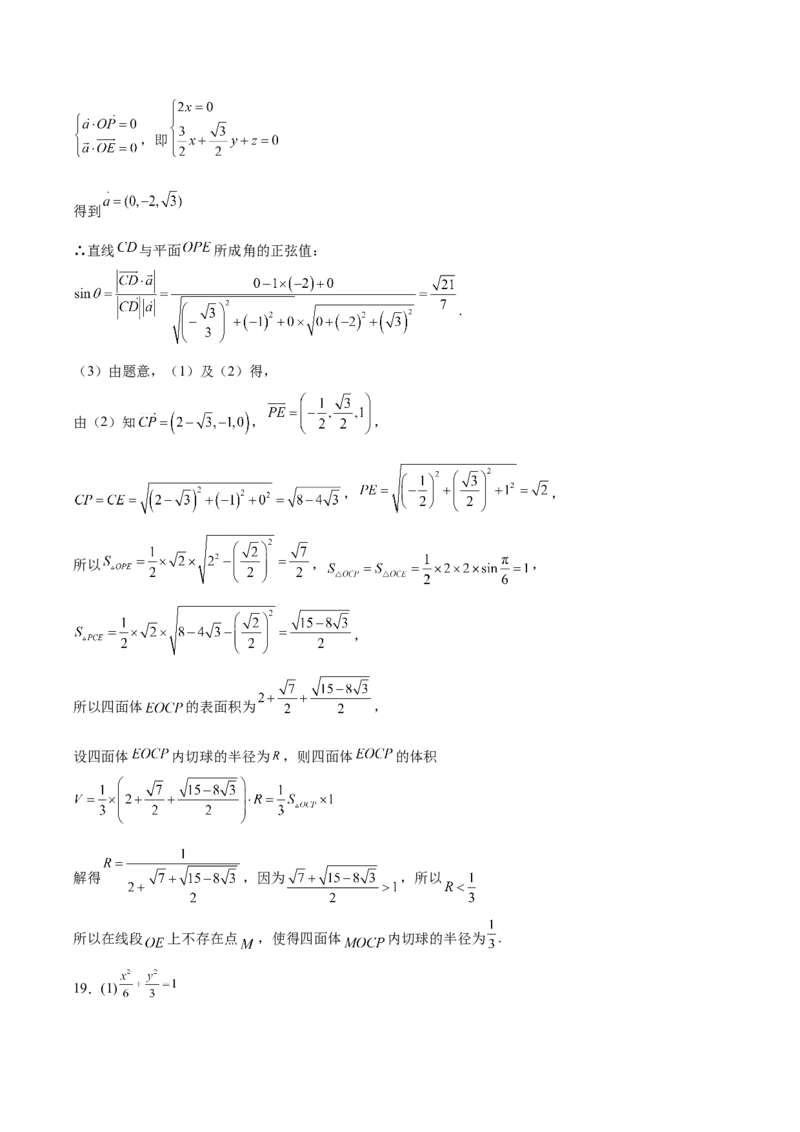文档内容
安徽师范大学附属中学2025-2026学年高二上学期11月期中
数学(A)试题
一、单选题
1.直线 的倾斜角为( )
A. B. C. D.
2.已知向量 , ,若 , ,则 ( )
A.-1 B.1 C.-2 D.2
3.已知直线 与直线 .“ ”是“ ”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
4.若圆 与圆 有三条公切线,则 ( )
A.21 B.19 C.9 D.
5.已知直线 ,从点 射出的光线经直线 反射后经过点 ,则光线从 到 的路
程为( )
A. B. C. D.
6.直三棱柱 中, , 、 分别是 、 的中点, ,则 与
所成的角的余弦值为( )
A. B. C. D.
7.已知 ,若直线 上存在点 ,使得 ,则 的取值范围为( )
A. B.C. D.
8.已知椭圆 的左、右焦点分别是 ,点 是椭圆 上位于第一象限的一点,且
与 轴平行,直线 与 的另一个交点为 ,若 ,则 的离心率为( )
A. B. C. D.
二、多选题
9.关于空间向量,下列说法正确的是( )
A.若 ,则 共线
B.已知 ,若 夹角为锐角,则
C.若对空间中任意一点 ,有 ,则 四点共面
D.若向量 能构成空间的一个基底,则 也能构成空间的一个基底
10.已知圆 过点 ,动点 直线 上任意一点,过 向圆 引两条切
线,切点分别为为 ,记 的最小值为 的最大值为 .下列说法正确的是( )
A.圆 的标准方程为
B.
C.四边形 的面积范围为
D.当 时,四边形 的外接圆与圆 的交点所在的直线为
11.已知正方体 的棱长为 ,其中 ,点 为线段 的中点,则下列选项正确的是( )
A. 时,
B. 时,三棱锥 的体积为定值
C.当点 落在以 为球心, 为半径的球面上时, 的最小值为1
D. 时,直线 与面 的交点轨迹长度为
三、填空题
12.在空间直角坐标系中,已知 ,则点 到直线 的距离为 .
13.古希腊著名数学家阿波罗尼斯发现了平面内到两个定点 的距离之比为定值 的点的轨迹是
圆,此圆被称为“阿波罗尼斯圆”.在平面直角坐标系中,已知 , ,若动点P满足 ,
设点 的轨迹为 ,过点 作直线 , 上恰有三个点到直线 的距离为1,则满足条件的一条直线 的
方程为 .
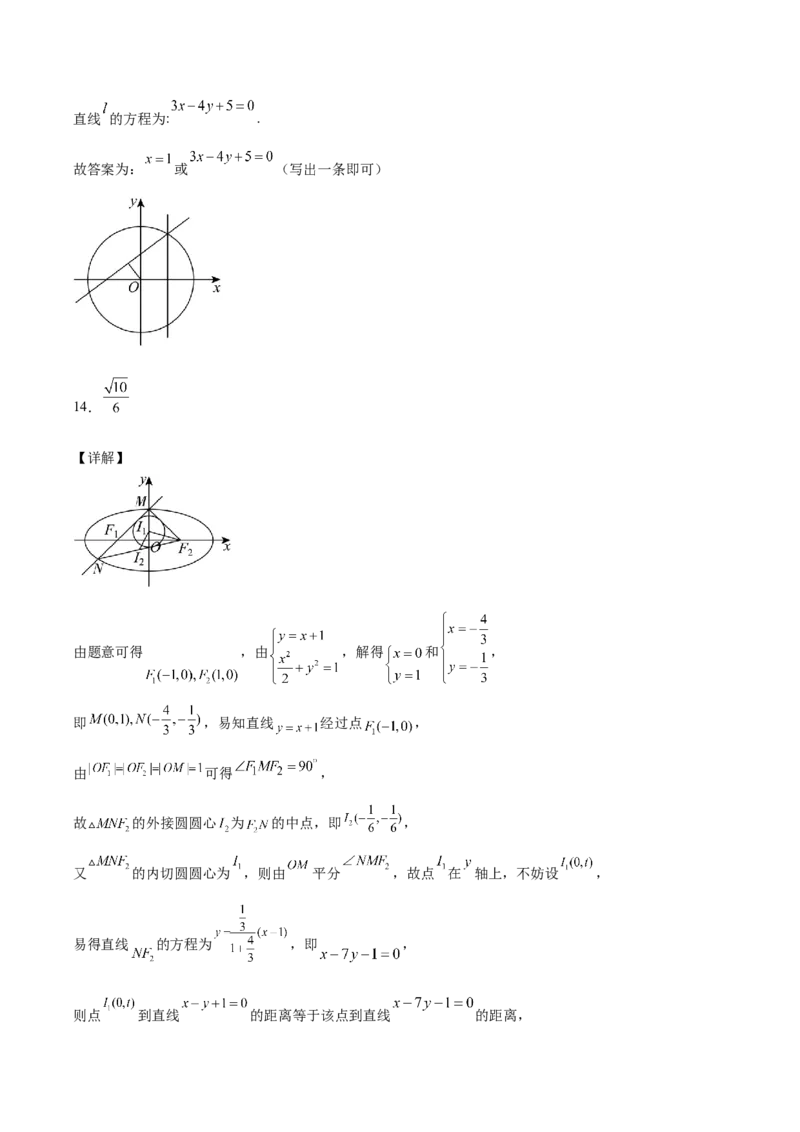
14.已知椭圆 的左、右焦点分别为 ,直线 与C交于M,N两点,设 的内切
圆圆心为 ,外接圆圆心为 ,则 的值为 .
四、解答题
15.已知 为实数,设直线 .
(1)若 ,求 的值;
(2)若 ,求 与 的距离.16.已知圆 过两点 ,且圆心 在直线 上.
(1)求圆 的标准方程;
(2)若过圆心 的直线 在 轴, 轴上的截距是互为相反数,求直线 的方程.
17.已知圆 ,圆 ,过点 作圆 的切线,切线的长
为2.
(1)求圆 的方程;
(2)直线 经过点 ,且与圆 交于 两点, ,求 的方程和 的值.
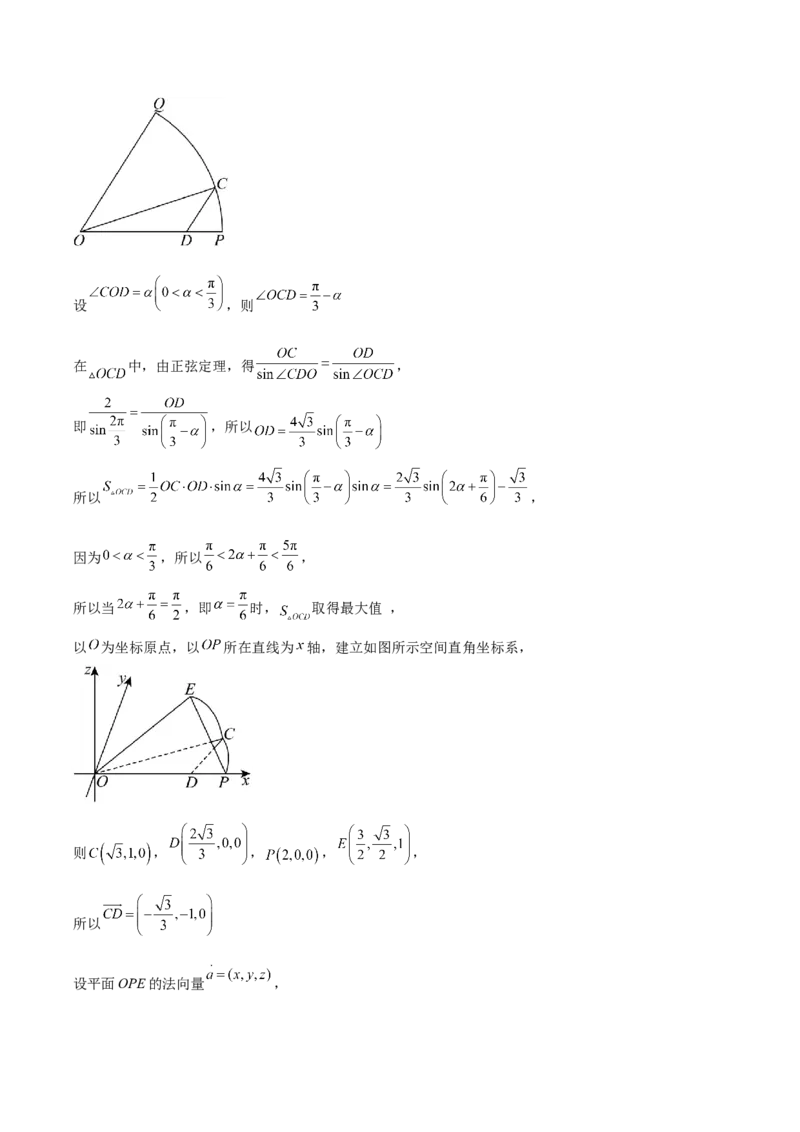
18.如图1,在半径为2的扇形 中, , 是弧PQ上的动点(不含 , ),过点 作
,交 于点 .
(1)当 时,求此时 的长;
(2)当 的面积取得最大值时,将扇形 沿着 折起到 ,使得平面 平面 (如图2
所示).求此时直线 与平面 所成角的正弦值;
(3)在第(2)问的条件下,探究在图2中的线段 上是否存在点 ,使得四面体 内切球的半径为
?并说明理由.
19.已知椭圆 的离心率为 ,且过点 .
(1)求椭圆 的方程;
(2) , 为椭圆 上两个不同的点,且 ,
①求证:直线 恒过定点,并求出该定点的坐标;②过 点作直线 的垂线,垂足为 ,求 的最大值.参考答案
1.B
【详解】直线 化为点斜式得, ,
所以直线的斜率为 ,所以倾斜角为 ,
故选:B.
2.A
【详解】 , , ,
, , , ,
.
故选:A.
3.A
【详解】 和 平行,
,
或 .
当 时, , , ;
当 时, , , .
“ ”是“ ”的充分不必要条件.
故选:A.
4.C
【详解】圆 的圆心 ,半径 ,
圆 的圆心 ,半径 ,
由圆 与圆 恰有三条公切线,得圆 与圆 外切,则即 ,解得 ,
故选:C
5.D
【详解】设点 关于直线 的对称点为 ,
则有 ,解得 ,即
因为光线从A到 的路程即 的长,而 .
所以光线从A到 的路程为 .
故选:D.
6.C
【详解】由题意可知 平面 ,且 ,以点 为坐标原点, 、 、 所在直线分
别为 、 、 轴建立如下图所示的空间直角坐标系,
设 ,则 、 、 、 ,
, , .故 与 所成的角的余弦值为 .
故选:C.
7.C
【详解】设 ,
,即 ,
化简得 ,
故点 在以 为圆心,1为半径的圆上,
∵若直线 上存在点 ,使得 ,
∴直线 与圆 有交点,
∴圆心到直线 的距离为 ,
两边同时平方,得 ,
继续化简得 ,解得 .
故选:C.
8.B
【详解】由 令 ,得 ,
由于 与 轴平行,且 在第一象限,所以 .
由于 ,
所以 ,即 ,将 点坐标代入椭圆 的方程得 ,
,
,
所以离心率 .
故选:B
9.ACD
【详解】对于A,若 ,则 ,即 ,则 共线;
A正确;
对于B ,且 与 不共线,解得: ,且 ,B不正确;
对于 四点共面,C正确;
对于D,假设 也能构成空间的一个基底,
则存在实数 ,使得 ,
方程组无解,
不共面, 可以构成空间的一组基底,D正确.故选:ACD.
10.AD
【详解】对于A项,因为圆 过 ,且 的中点坐标为 ,
故 ,且
该点 与 的三点距离相等,所以 为圆 的圆心,即 ,
且圆 的半径 .
所以圆 的标准方程为 ,故A项正确.
对于B项,因为 ,所以易证 ,所以
,
又因为 ,所以 ,结合 在 单调递减,
又因为 ,当且仅当 最小时, 取最小值,
即 ,此时 , ,
,即
此时 最大,且 最大值是一个钝角,
因为 为直线 上的一个动点, 可以一个锐角连续变化一个钝角,
所以,当 时, ,所以 ,故B项错误.对于C项,因为 ,所以
,
所以当 时,即 , ,故C项错误.
对于D项,因为 ,所以 四点共圆.
当 时,此时 ,所以直线 ,
又因为 ,解得 ,此时 ,
四点共圆的圆心 ,半径为 ,所以圆 ,
联立圆 减去圆 的方程得直线: ,故D项正确.
故答案为:AD.
11.ABD
【详解】如图,建立以 为原点的空间直角坐标系.则
.A选项,因
,则 ,
又 ,则 .
又 ,则 ,即 ,故A正确.
B选项, ,设平面 法向量为 ,则 ,取 ,又 时, ,
则 ,即 平行于平面 ,得点 到平面 距离 为定值,
故 为定值.故B正确;
C选项,因 ,点 落在以 为球心, 为半径的球面上,
则 ,
令 ,因为 ,则 .
则 ,
当且仅当 时取等号,则 的最小值为 ,故C错误.
D选项,因 ,
则 ,
即点 在线段 上.连接 ,分别交 于 ,
故 ,即 为交点轨迹.又 ,
则 .故D正确.故选:ABD.
12.
【详解】由题意 , ,
所以 在 的射影为: .
所以点 到直线 的距离为: .
故答案为:1
13. 或 (写出一条即可)
【详解】因为 ,点 满足 ,设 ,
则 ,化简得 ,
因为圆 上恰有三个点到直线 的距离为1,
所以圆心到直线的距离为1.
若直线 的斜率不存在,
直线 的方程为 ;
若直线 的斜率存在,
设直线 的方程为 ,
即 , ,解得 ,直线 的方程为: .
故答案为: 或 (写出一条即可)
14.
【详解】
由题意可得 ,由 ,解得 和 ,
即 ,易知直线 经过点 ,
由 可得 ,
故 的外接圆圆心 为 的中点,即 ,
又 的内切圆圆心为 ,则由 平分 ,故点 在 轴上,不妨设 ,
易得直线 的方程为 ,即 ,
则点 到直线 的距离等于该点到直线 的距离,即 ,解得 或 (不合题意,舍去),故得 ,
故 .
故答案为: .
15.(1)
(2)
【详解】(1)因为 ,解得 .
(2)因为 ,所以 ,解得 ,
此时 ,即
由两直线之间的距离公式
16.(1)
(2) 或
【详解】(1)由 可知中点 ,
设过 的 中垂线 斜率为 ,
,则 .
所以 ,即
由 ,解得 ,故 ,圆 的半径为 ,
故圆 的标准方程为
(2)①若直线 过原点,满足题意,则可设 ,
因为直线 过 ,所以 ,则 .
②若直线 不过原点,由于直线 在 轴, 轴上的截距是互为相反数,
设 ,因为直线 过 ,
所以 ,则 ,即
综上所述:直线的方程为 或 .
17.(1)
(2)1
【详解】(1)过点 作圆 的切线,设切点为 ,连接 ,
因为 ,
所以 ,
所以圆 .
(2)显然,直线 的斜率存在,设直线 的方程为 ,设圆心 到直线 的距离为 ,
所以 ,解得 ,
又因为 ,整理得, ,
解得 或 ,
所以 的方程为 或 ;
在 中, ,
所以 .
18.(1) ;
(2) ;
(3)不存在,理由见解析.
【详解】(1)由题意,
, , ,
∴ , ,
在 中, ,
由正弦定理 ,代入数据解得:
(2)由题意及(1)得,
因为 , ,所以 ,设 ,则
在 中,由正弦定理,得 ,
即 ,所以
所以 ,
因为 ,所以 ,
所以当 ,即 时, 取得最大值 ,
以 为坐标原点,以 所在直线为 轴,建立如图所示空间直角坐标系,
则 , , , ,
所以
设平面OPE的法向量 ,,即
得到
∴直线 与平面 所成角的正弦值:
.
(3)由题意,(1)及(2)得,
由(2)知 , ,
, ,
所以 , ,
,
所以四面体 的表面积为 ,
设四面体 内切球的半径为 ,则四面体 的体积
解得 ,因为 ,所以
所以在线段 上不存在点 ,使得四面体 内切球的半径为 .
19.(1)(2)①证明见解析,定点坐标为 ;② .
【详解】(1)由题意知 ,故 ,即 ,
又因为椭圆过点 ,所以 ,解得 ,
所以椭圆 的方程为: .
(2)①设 , ,
,
(i)当直线 斜率不存在时,设 ,
联立 得 ,
,
解得 (舍)或 ,此时 .
(ii)当直线 斜率存在时,设 ,
联立 得 ,
.
又 ,
,整理得 ,
将 代入整理得 ,
,
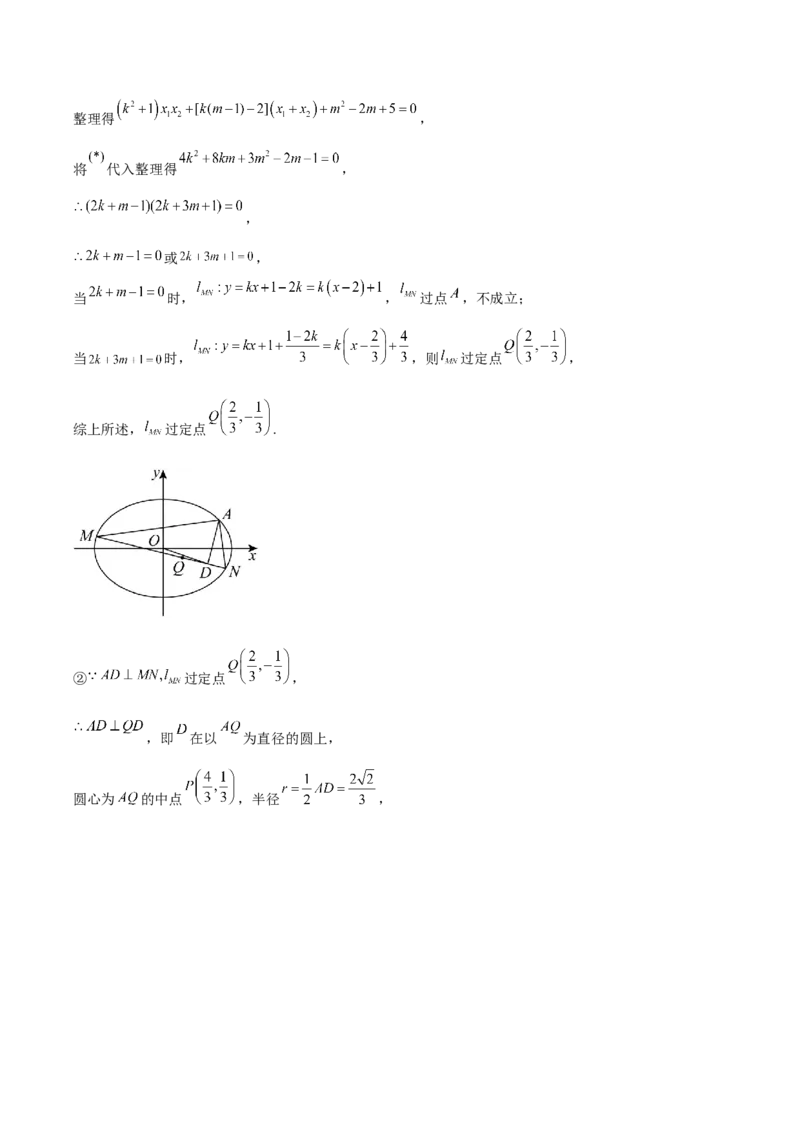
或 ,
当 时, , 过点 ,不成立;
当 时, ,则 过定点 ,
综上所述, 过定点 .
② 过定点 ,
,即 在以 为直径的圆上,
圆心为 的中点 ,半径 ,