文档内容
成都石室中学 2024-2025 年度下期高 2024 届二诊模拟考试
数学试题(文)(A 卷)参考答案
一、选择题:
1
z=
1.已知复数 1+i(其中i为虚数单位),则z的虚部是
1 1 1 1
− − i i
2 2 2 2
A. B. C. D.
1 1−i 1
z= = −
1.A 1+i 2 ,所以z的虚部是 2 .
{ 1}
A={1,2},B= y|y=x2
2.若集合 ,则 a∈A 是a∈B的
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
2.A B=[0,+∞) ,则A是B的真子集,则 a∈A 是a∈B的充分不必要条件.
3.如图是根据某校高三8位同学的数学月考成绩(单位:分)画出的茎叶图,其中左边的数字从左到右
分别表示学生数学月考成绩的百位数字和十位数字,右边的数字表示学生数学月考成绩的个位数字,则
下列结论正确的是 11 8 7 7
A.这8位同学数学月考成绩的极差是14
12 5 1 3
B.这8位同学数学月考成绩的中位数是122
13 1 2
C.这8位同学数学月考成绩的众数是118
D.这8位同学数学月考成绩的平均数是124
3.B 对于选项A,极差是 ,故A错误;
121+123
=122
2
对于选项B,中位数是 ,故B正确;
对于选项C,众数是117,故C错误;
对于选项D,平均数是 ,故D错误,故选B.
4.已知一个空间几何体的三视图如图所示,其中正视图、侧视图都是由
半圆和矩形组成,则这个几何体的体积是
3 5 7 9
π π π π
2 3 3 2
A. B. C. D.
4.A 还原成直观图后,几何体由一个圆柱和八分之三个球组成,故这个
1
学科网(北京)股份有限公司几何体的体积 .
5.已知数列 为等差数列,且 ,则 的值为
A.2 B.4 C.6 D.8
a +a +a +a +a =10 5a =10 a =2 a +a =4
5.B 因为 2 3 6 9 10 ,由等差数列的性质,得 6 , 6 ,所以 4 8 .
1 1
+ =1
6.若 a,b 是正实数,且3a+b 2a+4b ,则a+b的最小值为
4 2
A.5 B.3 C.1 D.2
1 1 ( 1 1 )
a+b= [(3a+b)+(2a+4b)]⋅1= [(3a+b)+(2a+4b)]⋅ +
6.A 因为
5 5 3a+b 2a+4b
1( 2a+4b 3a+b ) 4 3 1 4
= 2+ + ≥ a= ,b=
5 3a+b 2a+4b 5 ,当且仅当 5 5时取等号,所以a+b的最小值为5 .
π
00,b>0)
12.若双曲线 a2 b2 的左、右焦点分别为 F 1 ,F 2,过右焦点 F 2的直线 与双曲线C交于
(b )
A,B 两点,已知 的斜率为k,
k∈
a
,+∞
,且 |AF 2 |=2|F 2 B| , ∠F 1 AB=600 ,则直线AB的斜率是
√3
A. 2√3 B. √3 C. 3 D.2
|F B|=x |F A|=2x |F A|=2a+2x,|F B|=2a+x
12.A 设 2 ,则 2 ,由双曲线定义,得 1 1 .
a
在 ΔAF 1 B 中,由余弦定理,得 |F 1 B| 2 =|F 1 A| 2 +|AB| 2 −2|F 1 A||AB|cos600 ,解得 x= 3 .
√13
ΔAF F 4c2 =|F A| 2 +|F A| 2 −2|F A||F A|cos600
e=
3
在 1 2中,由余弦定理,得 1 2 1 2 ,解得 .
7
学科网(北京)股份有限公司x2 y2 ( 2)
C: − =1 x=my−√13t 00)
,则
c=√13t,b=2t
,
9t2 4t2
,设 :
3
,联立
x2 y2 8√13mt 16t2
− =1 y +y = ,y y =
9t2 4t2 , ,得 (4m2 −9)y2 −8√13mty+16t2 =0 , 1 2 4m2 −9 1 2 4m2 −9 .
1
|AF|=2|F B| y =−2y
m=
2√3 k =2√3
由 2 2 ,得 1 2,则 ,所以 AB .
b2 b2
a a
|AF|= |BF|=
法二:设直线倾斜角 为α,由双曲线第二定义得: 2 1−ecosα, 2 1+ecosα ,又
|AF
2
|=2|F
2
B|
,则
e=√1+k
A
2
B
| 2
1
−
+2
1 |
,又
k∈ (b
a
,+∞ )
,则
k
AB
=2√3
.
二、填空题:
13.已知向量
⃗a=(1,−2)
,
⃗b=(2,x)
,若
⃗a⊥ ⃗b
,则实数x= .
13.1 因为 ⃗a⊥ ⃗b ,所以 ,解得x=1 .
14.已知实数x,y满足约束条件 ,则 z=3x+2y 的最大值是 .
14.3 作出x,y满足的可行域如图中阴影部分所示,作出直线 并平移,当直线过点 时,
z=3x+2y
,所以 的最大值是3.
8
学科网(北京)股份有限公司(1) n
S =x⋅ +27
n 3 a a ⋯a
15.已知等比数列 的前 项和为 ,若 ,则 1 2 n取最大值时,n的值为
.
a a 1
S = 1 − 1 ⋅qn x=−27,q=
15.3 等比数列 的公比为 ,由等比数列前n项和公式 n 1−q 1−q ,得 3 .又
a 1 =18 ,则
a
n
=18⋅ (
3
1) n−1
, a 2 =6,a 3 =2,a 4 = 3
2
,所以 a 1 a 2 ⋯a n取最大值时,n的值是3.
x2 +1
ln ≤ex −x2 −mx−1
16.若 x≥1 ,恒有 ex −mx ,则m的取值范围是 .
x2 +1
ln ≤ex −x2 −mx−1
16. 由 ex −mx ,得 ex −mx>0 在 x≥1 上恒成立,即m≤e.
且 ,即 .因为
y=lnx+x
在 上是增函数,所以 ,所以 .令 ,则
,所以 在 上单调递增, ,所以 .
三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。
17.(12分)
为了去库存,某商场举行如下促销活动:有两个摸奖箱, 箱内有1个红球、1个黑球、8个白球, 箱
内有4个红球、4个黑球、2个白球,每次摸奖后放回.消费额满300元有一次 箱内摸奖机会,消费额
满600元有一次 箱内摸奖机会.每次机会均为从箱子中摸出1个球,中奖规则如下:红球奖50元代金券、
黑球奖30元代金券、白球奖10元代金券.
ξ
(Ⅰ)某三位顾客各有一次 箱内摸奖机会,求中奖10元代金券人数 的分布列;
(Ⅱ)某顾客消费额为600元,请问:这位顾客如何抽奖所得的代金券期望值较大?
9
学科网(北京)股份有限公司1
解:(Ⅰ)三位顾客每人一次 箱内摸奖中10元代金券的概率都为5 ,
1
B(3, )
中奖10元代金券的人数 ξ 服从二项分布 5 ,
P(ξ=k)=Ck(1) k
⋅
(4) 3−k
,k=0,1,2,3
3 5 5
……………………………………4分
,
ξ
故 的分布列为
ξ 0 1 2 3
64 48 12 1
P
125 125 125 125
…………6分
(Ⅱ)可以在 箱摸奖2次,或者在 箱内摸奖1次
1 1 8
50× +30× +10× =16
10 10 10
箱摸奖1次所得奖金的期望值为 …………………………8分
,
4 4 2
50× +30× +10× =34
10 10 10
箱摸奖1次所得奖金的期望值为 , ………………………10分
箱摸奖2次所得奖金的期望值为2×16=32
, 箱摸奖1次所得奖金的期望值为34,
所以这位顾客选 箱摸奖1次所得奖金的期望值较大.…………………………………………12分
17.(文)某校从高二年级学生中随机抽取60名学生,将他们的期中成绩(均为整数)分成六段,
, 后得到如图所示的频率分布直方图,观察图形,回答下列问题:
(1)求 ,并估计此次期中考试成绩的众数.
(2)利用分层抽样的方法从样本中成绩在 和 两个分数段内的学生中抽5人,再从这5人中
随机抽取2人,求这2名学生的数学成绩之差的绝对值不大于10的概率.
10
学科网(北京)股份有限公司【详解】(1)由直方图知: ,则 ,
由图知:区间 的频率最大,故众数为75. …………………………4分
(2)成绩在 分数段的人数有 ,成绩在 分数段的人数有 ,
采用分层抽样的方式,在 抽取 人,记为A,B,C, 抽取 人,记为1,2,
从这5人中随机抽取两人,所有的基本事件有
共10种,……………………………………8分
2名学生的数学成绩之差的绝对值不大于10等价于这2个同学在同一个分数段.
记“这2名学生的数学成绩之差的绝对值不大于10”为事件N,
则事件N包含的基本事件有 共4种,…………10分
所以所求概率为 . ……………………………………………12分
18.(12分)
f(x)=λ
已知 ,设 .
f(x)
(Ⅰ)求函数 的对称中心;
2√3 √3
f(A)=
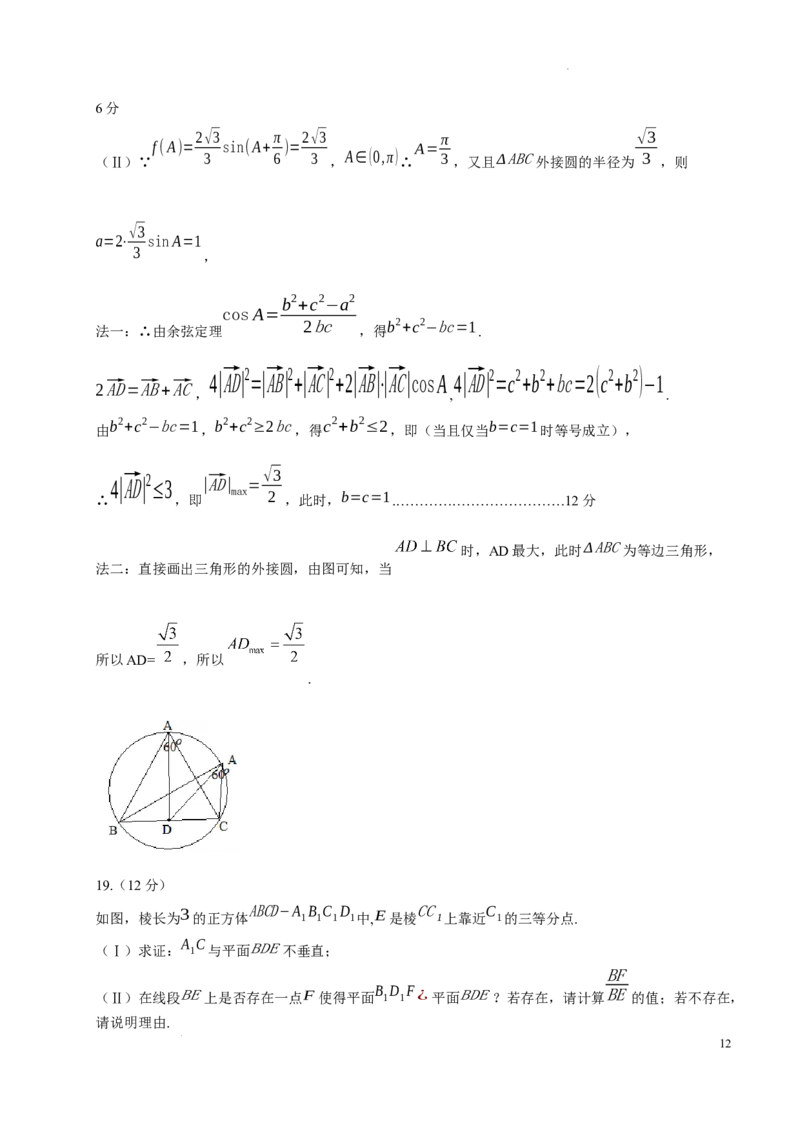
(Ⅱ)若ΔABC 中,角 A,B,C 所对的边分别为 a,b,c , 3 ,且ΔABC 外接圆的半径为 3 ,D
是 BC 边的中点,求线段AD长度的最大值.
{
sinx=m
√3 √3 2√3 π
λ=m+ cosx f(x)=sinx+ cosx= sin(x+ )
3 3 3 6
解:(Ⅰ)由 ,得 .
π π π
x+ =kπ,k∈Z x=kπ− ,k∈Z (kπ− ,0),k∈Z.
6 6 f (x) 6
令 ,解得 ,所以函数 的对称中心为 ……
11
学科网(北京)股份有限公司6分
2√3 π 2√3 π √3
f(A)= sin(A+ )= A=
(Ⅱ)∵ 3 6 3 , A∈(0,π) ∴ 3 ,又且ΔABC 外接圆的半径为 3 ,则
√3
a=2⋅ sinA=1
3
,
b2 +c2 −a2
cosA=
法一:∴由余弦定理
2bc
,得
b2 +c2 −bc=1
.
4| ⃗AD | 2 =| ⃗AB | 2 +| ⃗AC | 2 +2| ⃗AB |⋅| ⃗AC | cosA 4| ⃗AD | 2 =c 2 +b 2 + bc =2(c 2 +b 2) −1
2⃗AD= ⃗AB+ ⃗AC
, , .
由 b2 +c2 −bc=1 , b2 +c2 ≥2bc ,得 c2 +b2 ≤2 ,即(当且仅当b=c=1时等号成立),
√3
4| ⃗AD | 2 ≤3 | ⃗AD| =
∴ ,即 max 2 ,此时,b=c=1 .………………………………12分
时,AD最大,此时ΔABC
为等边三角形,
法二:直接画出三角形的外接圆,由图可知,当
所以AD= ,所以
.
19.(12分)
如图,棱长为 3 的正方体 ABCD−A 1 B 1 C 1 D 1中,E是棱 CC 1上靠近 C 1的三等分点.
A C
(Ⅰ)求证: 1 与平面BDE不垂直;
BF
(Ⅱ)在线段BE上是否存在一点F使得平面 B 1 D 1 F ¿平面BDE?若存在,请计算 BE 的值;若不存在,
请说明理由.
12
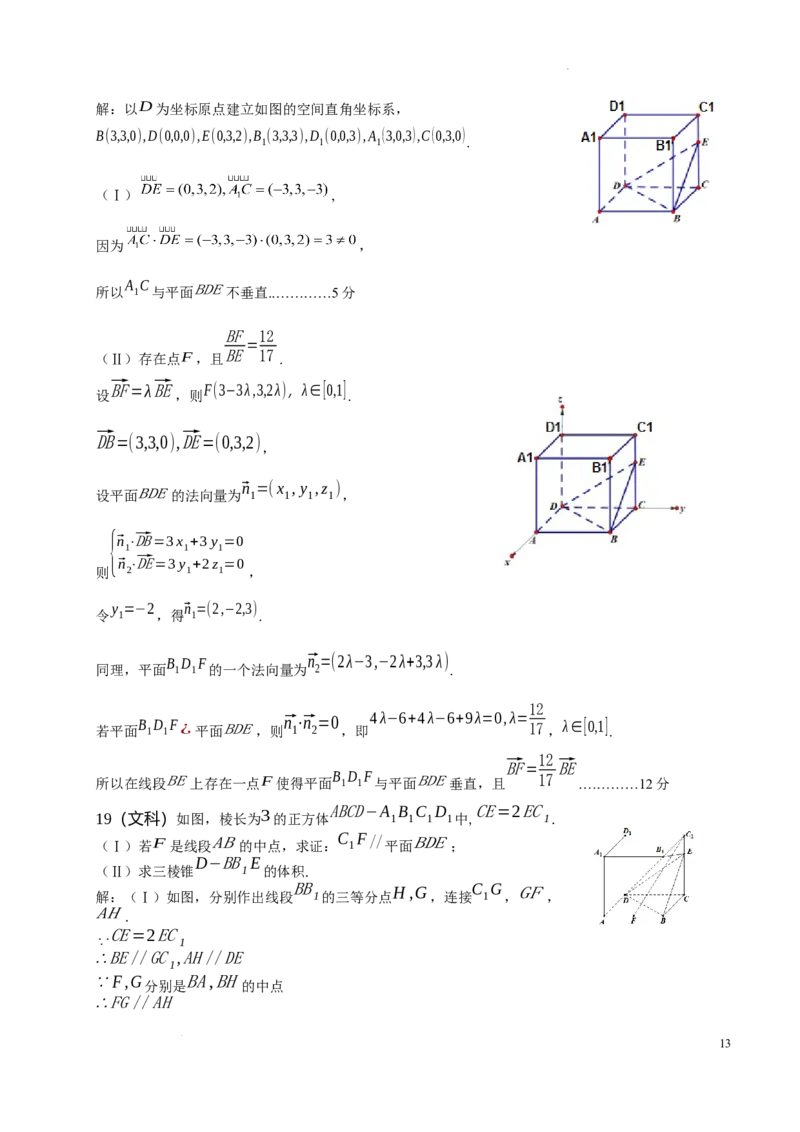
学科网(北京)股份有限公司解:以D为坐标原点建立如图的空间直角坐标系,
B(3,3,0),D(0,0,0),E(0,3,2),B (3,3,3),D (0,0,3),A (3,0,3),C(0,3,0)
1 1 1 .
(Ⅰ) ,
因为 ,
A C
所以 1 与平面BDE不垂直..…………5分
BF 12
=
(Ⅱ)存在点F,且 BE 17 .
⃗BF=λ⃗BE F(3−3λ,3,2λ),λ∈[0,1]
设 ,则 .
⃗DB=(3,3,0),⃗DE=(0,3,2)
,
设平面BDE的法向量为 ⃗n 1 =(x 1 ,y 1 ,z 1 ) ,
{⃗n⋅⃗DB=3x +3y =0
1 1 1
⃗n⋅⃗DE=3y +2z =0
则 2 1 1 ,
y =−2 ⃗n =(2,−2,3)
令 1 ,得 1 .
B D F ⃗n =(2λ−3,−2λ+3,3λ)
同理,平面 1 1 的一个法向量为 2 .
12
若平面 B 1 D 1 F ¿平面BDE,则 ⃗n 1 ⋅⃗n 2 =0 ,即 4λ−6+4λ−6+9λ=0,λ= 17 , λ∈[0,1] .
12
⃗BF= ⃗BE
所以在线段BE上存在一点F使得平面 B 1 D 1 F 与平面BDE垂直,且 17 .…………12分
3
ABCD−A B C D CE=2EC
19(文科)如图,棱长为 的正方体 1 1 1 1中, 1.
(Ⅰ)若F是线段 AB 的中点,求证:
C
1
F//
平面 BDE ;
D−BB E
(Ⅱ)求三棱锥 1 的体积.
BB H,G C G GF
解:(Ⅰ)如图,分别作出线段 1的三等分点 ,连接 1 , ,
AH
.
CE=2EC
∵ 1
∴BE//GC ,AH//DE
1
∵F,G BA,BH
分别是 的中点
∴FG//AH
13
学科网(北京)股份有限公司∴FG//DE
∵FG∩GC =G
又 1
GFC //
∴平面 1 平面EBD
∵C F⊂ GFC
1 平面 1
C F//
BDE
∴ 1 平面 …………………………………………………………………………………………6分
1 1 1 9
V = S ¿DC= × ×3×3×3=
(Ⅱ) D−BEB 1 3 ΔBEB 1 3 2 2 …………………………………………………12
分
20.(12分)
x2 y2
E: + =1(a>b>0)
已知点F是椭圆 a2 b2 的右焦点,过原点的直线交椭圆E于 A,B 两点,ΔABF面积的最
√3
大值为 , .
(Ⅰ)求椭圆E的标准方程;
(Ⅱ)已知过点 P(4,y 0 ) 的直线l与椭圆E交于 M,N 两点,是否存在定点P,使得直线 FM,FN 的斜率
之和为定值?若存在,求出定点P的坐标及该定值.若不存在,请说明理由.
1
S = |OF||y −y |≤bc
解:(Ⅰ)因为 ΔABF 2 A B ,当且仅当 A,B 是y轴与椭圆的交点时取等号,
bc=√3 b2 =3,a2 =4
所以 .又 ,所以 ,
所以椭圆E的标准方程为 ………………………4分
.
(Ⅱ)设直线 的方程为 由 在直线 上,得
联立 化简得
.
14
学科网(北京)股份有限公司由根与系数的关系,得 ………………7分
由 ,得 .
故直线 的斜率之和为
…………9分
……..11分
要使上式为定值,则 故 且 ……..12分
,
21.(12分)
已知函数
f(x)=x2 −ax,x>0.
[a,2a+1]
(Ⅰ)是否存在实数a使得 在区间 上恒成立,若存在,求出a的取值范围,若不存
在,请说明理由;
h(x)=f(x)−a2lnx (1,ea
)
(Ⅱ)求函数 在区间 上的零点个数(e为自然对数的底数).
解:(Ⅰ)
f(x)=x2 −ax,x>0.
,因为 在区间
[a,2a+1]
上恒成立,
{2a+1>a>0
f(a)≥0
f(2a+1)≥0
所以 ,所以a>0,
[a,2a+1]
故对任意的a>0都能满足 在区间 上恒成立.…………………………4分
(Ⅱ) 由区间
(1,ea )
得
ea >1
,所以
a>0
.
a2 2x2 −ax−a2 (2x+a)(x−a)
h' (x)=2x−a− = = (x>0)
x x x
15
学科网(北京)股份有限公司h(x) (0,a) (a,+∞) h(x) =h(a)=−a2lna
所以 在 上单调递减,在 上单调递增, min .……6分
下面先证明:
00) g' (a)=ea −1(a>0)
设 ,则 ,
[0,+∞)
由 得 ,所以 在 上是增函数,故 .
所以
ea >a
.……………………………7分
h(x) =h(a)=−a2lna
min ,
①当−a2lna>0 ,即01时, 10(a>1)
下面证明 .
m(x)=e2x −xex −x3 (x>1) m' (x)=2e2x −ex −xex −3x2 (x>1)
令 ,则 ,
ϕ(x)=2e2x −ex −xex −3x2 (x>1) ϕ' (x)=4e2x −2ex −xex −6x(x>1)
令 ,则 ,
F(x)=4e2x −2ex −xex −6x(x>1)
令 ,
F' (x)=8e2x −3ex −xex −6=(3e2x −3ex )+(2e2x −xex )+(3e2x −6)>0
则 ,
F(x) (1,+∞) F(x)>F(1)=4e2 −3e−6>0
所以 在 上单调递增, ,
ϕ(x) (1,+∞)
所以 在 上单调递增, ,
m(x) (1,+∞) m(x)>m(1)=e2 −e−1>0
所以 在 上单调递增, ,
16
学科网(北京)股份有限公司h(ea )=e2a −aea −a3 >0(a>1)
所以 ,
h(x)
(1,ea
)
所以函数 在 上有一个零点. ……………………………………11分
h(x) h(x)
综上所述,当 时,函数 无零点;当 时,函数 有一个零点.…12分
22.(10分)
(1,0)
在平面直角坐标系 中,倾斜角为α的直线 过定点 ,以 为极点, 轴的非负半轴为极轴建
ρsin2θ=4cosθ
立极坐标系,曲线 的极坐标方程为 ,直线 与曲线 相交于不同的两点 .
(Ⅰ)若 ,求线段 中点 的直角坐标;
(Ⅱ)若 ,求 的最小值.
解析:(Ⅰ)曲线 的普通方程为 ……1分
时,直线 的参数方程为 ( 为参数),
当
代入 得 ……2分
,
设 , 对应的参数为 , ,则 ……3分
,
所以 对应的参数为 , ……4分
代入参数方程,得点 的直角坐标 . ……5分
17
学科网(北京)股份有限公司(Ⅱ)将直线 的参数方程 ( 为参数)代入 得
, ,
∴ ,当且仅当 时取等号,
∴ 的最小值为 . ……10分
23.(10分)
f(x)=|x+1|
已知函数 .
f(x)+f(2x−1)