文档内容
2023 级高二下学期 3 月阶段考
数学(人教 A 版)试题 D
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分 150 分,考试时间 120 分钟.请
在答题卡上作答.
第Ⅰ卷(选择题 共 58 分)
一、选择题:本题共 8 小题,每小题满分 5 分,共 40 分,在每小题给出的四个选项中只有一
项符合题目要求.
1. ( )
A. 14 B. 16 C. 18 D. 24
2. 若椭圆 C: 的焦点和顶点分别是双曲线 E 的顶点和焦点,则双曲线 E 的标准方程为(
)
A. B. C. D.
3. 已知随机变量 ,且 ,则 ( )
A B. C. D.
4. “点 在圆 外”是“直线 与圆 相交”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
5. 编号为 1,2,3,4,5,6,7 七盏路灯,晚上用时只亮三盏灯,若任意两盏亮灯不相邻,则不同的开
灯方案有( )
A. 10 种 B. 12 种 C. 15 种 D. 18 种
6. 已知点 的坐标为 ,动点 满足 , 为坐标原点,则 的最大值为( )
A. B. C. D.
7. 已知 是椭圆 上两点, 分别为 左、右焦点,
,则 的离心率为( )
第 1页/共 5页A. B. C. D.
8. 有甲、乙两个不透明的袋子,甲袋子里有 1 个白球,乙袋子里有 5 个白球和 5 个黑球,现从乙袋子里随
机取出 个球放入甲袋子里,再从甲袋子里随机取出一个球,记取到的白球的个数为 ,
则当 变大时( )
A. 变小 B. 先变小再变大
C. 变大 D. 先变大再变小
二、选择题:本题共 3 个小题,每小题 6 分,共 18 分.在每小题给出的选项中,有多项符合
题目要求.全部选对的得 6 分,有选错的得 0 分,部分选对的得部分分.
9. 已知 的展开式中第 4 项与第 5 项的二项式系数相等,则( )
A. B. 所有项的系数和为 1
C. 没有常数项 D. 的系数为 14
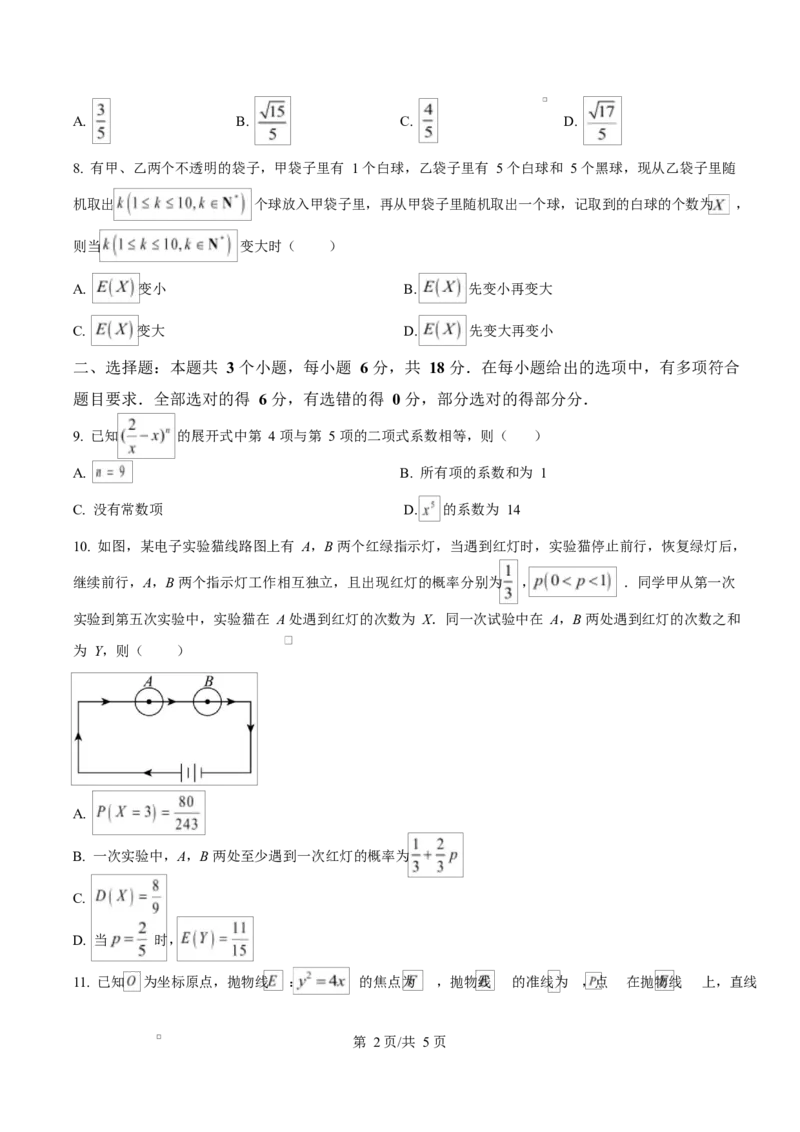
10. 如图,某电子实验猫线路图上有 A,B 两个红绿指示灯,当遇到红灯时,实验猫停止前行,恢复绿灯后,
继续前行,A,B 两个指示灯工作相互独立,且出现红灯的概率分别为 , .同学甲从第一次
实验到第五次实验中,实验猫在 A 处遇到红灯的次数为 X.同一次试验中在 A,B 两处遇到红灯的次数之和
为 Y,则( )
A.
B. 一次实验中,A,B 两处至少遇到一次红灯的概率为
C.
D. 当 时,
11. 已知 为坐标原点,抛物线 : 的焦点为 ,抛物线 的准线为 ,点 在抛物线 上,直线
第 2页/共 5页过点 且与 交于 , 两点,则( )
A. 若点 的坐标为 ,则 的最小值为 3
B. 以线段 为直径的圆与直线 相离
C. 点 到直线 的最小距离为
D. 可能为钝角三角形
第Ⅱ卷(非选择题 共 92 分)
三、填空题:本题共 3 小题,每小题 5 分,共 15 分.
12. 已知 ,设直线 , ,若 ,则 ______.
13. 已知点 在抛物线 上,且到 的焦点的距离为 ,则实数
__________.
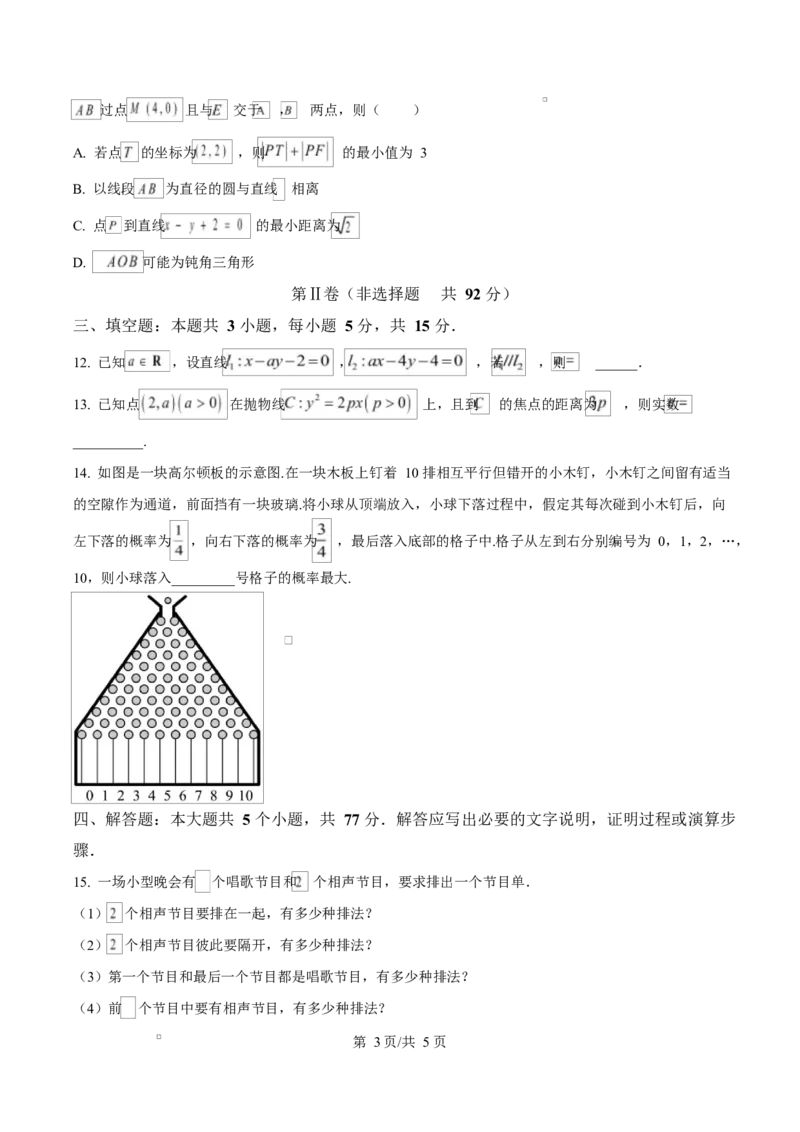
14. 如图是一块高尔顿板的示意图.在一块木板上钉着 10 排相互平行但错开的小木钉,小木钉之间留有适当
的空隙作为通道,前面挡有一块玻璃.将小球从顶端放入,小球下落过程中,假定其每次碰到小木钉后,向
左下落的概率为 ,向右下落的概率为 ,最后落入底部的格子中.格子从左到右分别编号为 0,1,2,…,
10,则小球落入_________号格子的概率最大.
四、解答题:本大题共 5 个小题,共 77 分.解答应写出必要的文字说明,证明过程或演算步
骤.
15. 一场小型晚会有 个唱歌节目和 个相声节目,要求排出一个节目单.
(1) 个相声节目要排在一起,有多少种排法?
(2) 个相声节目彼此要隔开,有多少种排法?
(3)第一个节目和最后一个节目都是唱歌节目,有多少种排法?
(4)前 个节目中要有相声节目,有多少种排法?
第 3页/共 5页(要求:每小题都要有过程,且计算结果都用数字表示)
16. 某校体育节组织比赛,需要志愿者参加服务 项目有:60 米袋鼠跳、100 米、200 米、1500 米、3000
米、4×100 米接力.
(1)志愿者小明同学可以在 6 个项目中选择 3 个项目参加服务,求小明在选择 60 米袋鼠跳服务的条件下,
选择 3000 米服务的概率;
(2)为了调查志愿者选择服务项目的情况,从志愿者中抽取了 15 名同学,其中有 9 名首选 100 米,6 名首
选 4×100 米接力.现从这 15 名同学中再选 3 名同学做进一步调查.将其中首选 4×100 米接力的人数记作 X
,求随机变量 X 的分布列和数学期望.
17. 如图,在正四棱锥 中, , 为侧棱 SD 的中点.
(1)求证: ;
(2)求点 到平面 PAC 的距离;
(3)求平面 SBC 与平面 PAC 夹角的余弦值.
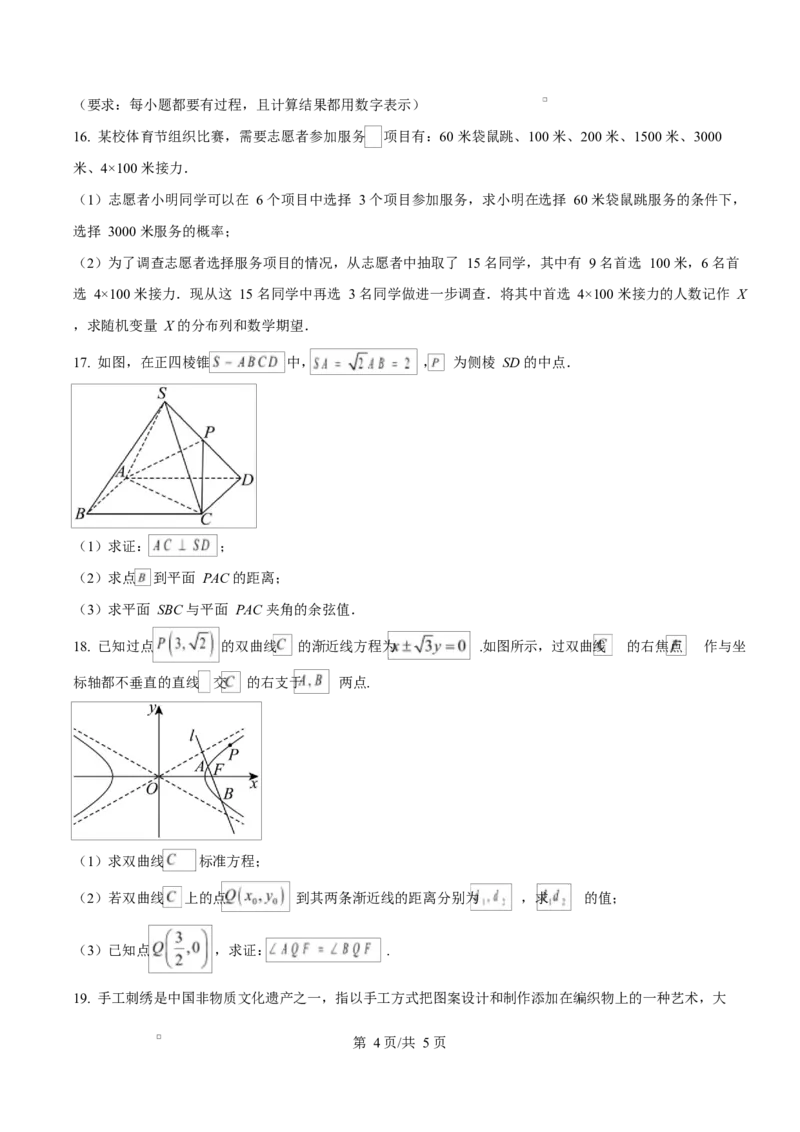
18. 已知过点 的双曲线 的渐近线方程为 .如图所示,过双曲线 的右焦点 作与坐
标轴都不垂直的直线 交 的右支于 两点.
(1)求双曲线 标准方程;
(2)若双曲线 上的点 到其两条渐近线的距离分别为 ,求 的值;
(3)已知点 ,求证: .
19. 手工刺绣是中国非物质文化遗产之一,指以手工方式把图案设计和制作添加在编织物上的一种艺术,大
第 4页/共 5页致分为三个环节,简记为工序 ,工序 ,工序 .经过试验测得小李在这三道工序成功的概率依次为 ,
, .现某单位推出一项手工刺绣体验活动,报名费 30 元,成功通过三道工序最终的奖励金额是 200 元,
为了更好地激发参与者的兴趣,举办方推出了一项工序补救服务,可以在活动开始前付费聘请技术员,若
某一道工序没有成功,可以由技术员完成本道工序,技术员只完成其中一道工序,且只能聘请一位技术员,
需另付聘请费用 100 元,若制作完成后没有接受技术员补救服务的退还一半的聘请费用.
(1)求小李独立成功完成三道工序的概率;
(2)若小李聘请一位技术员,且接受技术员补救服务,求他成功完成三道工序的概率;
(3)为了使小李获得收益的期望值更大,请问小李是否需要聘请一位技术员?请说明理由.
第 5页/共 5页