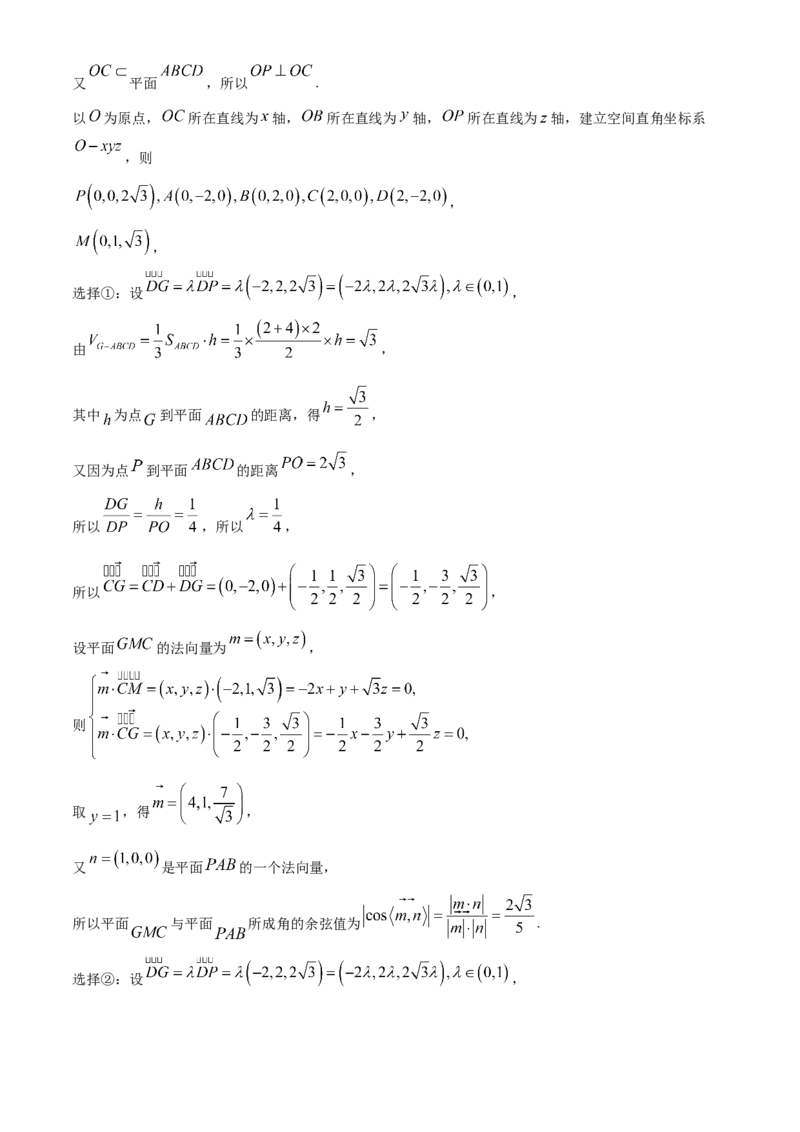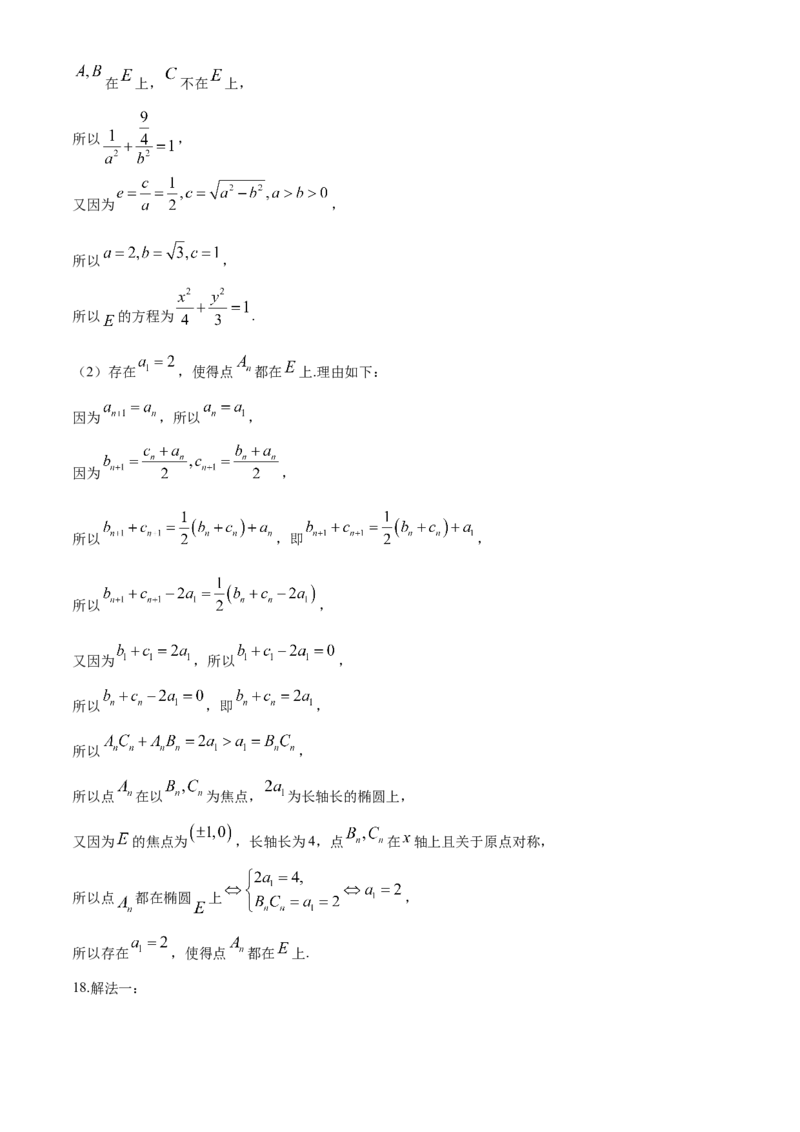文档内容
福建省漳州市 2024 届高三毕业班第四次教学质量检测
数学试题
本试卷共4页.满分150分.
考生注意:
1.答题前,考生务必在试题卷、答题卡规定的地方填写自己的准考证号、姓名.考生要认真核对
答题卡上粘贴的条形码的“准考证号、姓名”与考生本人准考证号、姓名是否一致.
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,
用橡皮擦干净后,再选涂其它答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷上
无效.
3.考试结束,考生必须将试题卷和答题卡一并交回.
一、单项选择题:本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只
有一项是符合题目要求的.
1.一组数据如下: ,该组数据的 分位数是( )
A.15 B.17 C.19 D.20
2.已知复数 ,则 ( )
A.2 B. C.1 D.0
3.二项式 展开式中, 项的系数为( )
A.-60 B.-15 C.15 D.60
4.设 ,且 ,则 的( )
A.最小值为-3 B.最小值为3
C.最大值为-3 D.最大值为3
5.已知函数 是函数 的导函数,则 ( )
A.1 B.2 C.3 D.4
6.已知数列 是公比不为1的正项等比数列,则 是 成立的( )
A.充要条件 B.充分不必要条件
C.必要不充分条件 D.既不充分也不必要条件
7.已知函数 ,则函数 的单调性( )
A.与 无关,且与 无关 B.与 无关,且与 有关
学科网(北京)股份有限公司C.与 有关,且与 无关 D.与 有关,且与 有关
8.已知双曲线 左、右焦点分别为 ,过 的直线与 的渐近线
及右支分别交于 两点,若 ,则 的离心率为( )
A. B.2 C. D.3
二、多项选择题:本大题共3小题,每小题6分,共18分,在每小题给出的四个选项中,有
多个选项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.已知函数 ,则下列说法正确的是( )
A.当 时, 的最小正周期为
B.当 时, 的最大值为
C.当 时, 在区间 上有4个零点
D.若 在 上单调递减,则 的取值范围为
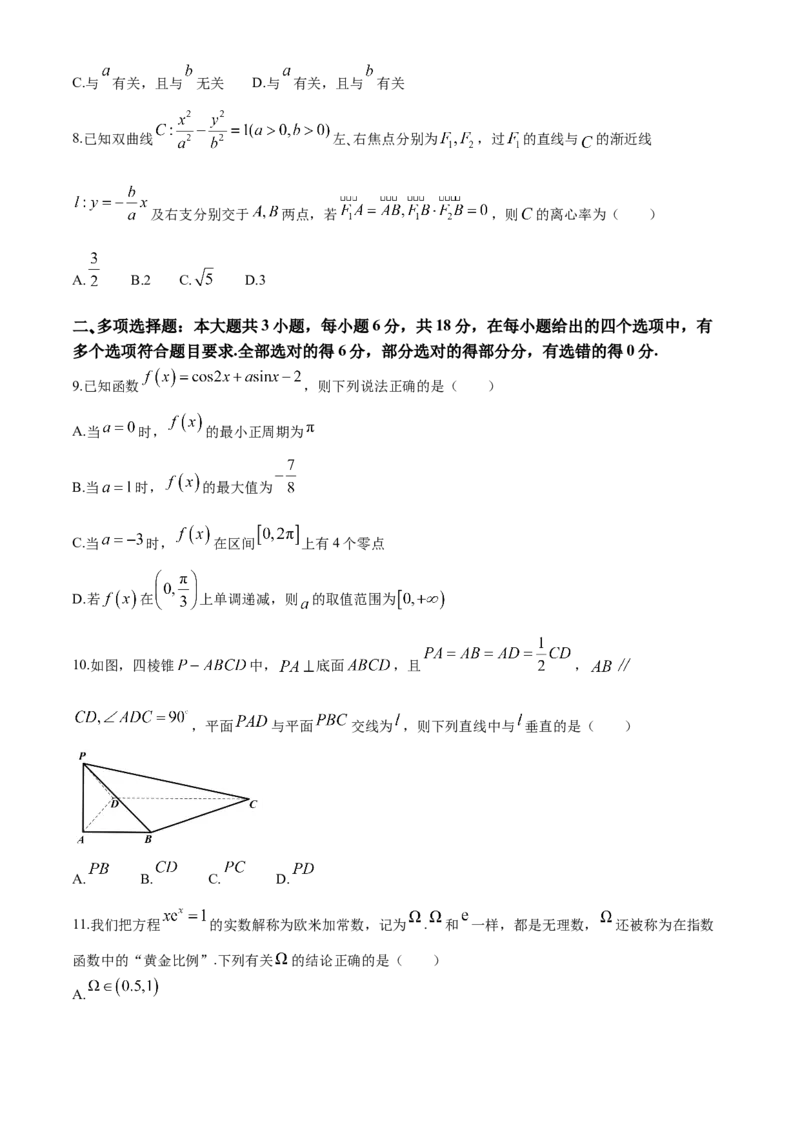
10.如图,四棱锥 中, 底面 ,且 ,
,平面 与平面 交线为 ,则下列直线中与 垂直的是( )
A. B. C. D.
11.我们把方程 的实数解称为欧米加常数,记为 . 和 一样,都是无理数, 还被称为在指数
函数中的“黄金比例”.下列有关 的结论正确的是( )
A.
学科网(北京)股份有限公司B.
C. ,其中
D.函数 的最小值为
三、填空题:本大题共3小题,每小题5分,共15分.
12.写出过点 且与抛物线 有唯一公共点的一条直线方程__________.
13.已知向量 ,且 在 上的投影向量的坐标为 ,则 与 的夹角为__________.
14.在矩形 中, 为 的中点,将 沿 折起,把 折成 ,使
平面 平面 ,则三棱锥 的外接球表面积为__________.
四、解答题:本大题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(13分
记 的内角 的对边分别为 ,已知 .
(1)若 成等差数列,求 的面积;
(2)若 ,求 .
16.(15分)
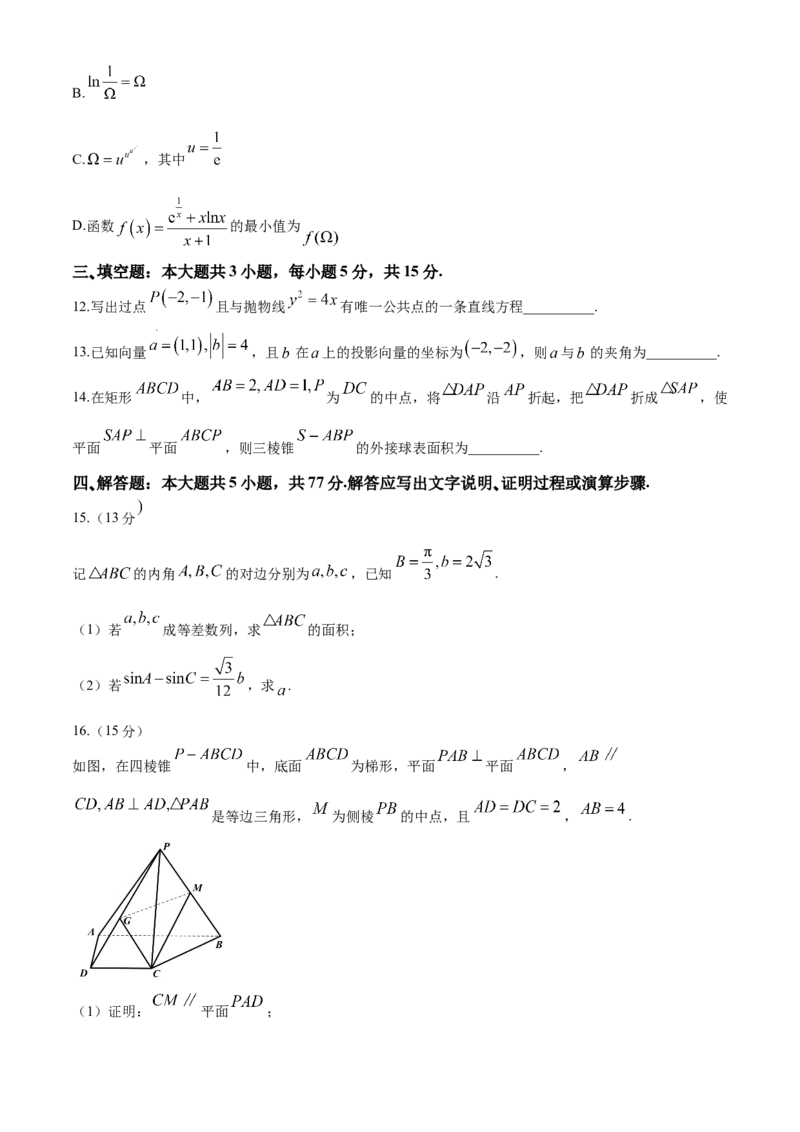
如图,在四棱锥 中,底面 为梯形,平面 平面 ,
是等边三角形, 为侧棱 的中点,且 , .
(1)证明: 平面 ;
学科网(北京)股份有限公司(2) 是线段 上异于端点的一点,从条件①、条件②中选择一个作为已知,求平面 与平面
所成角的余弦值.
条件①:四棱锥 的体积为 ;
条件②:点 到平面 的距离为 .
注:如果选择多个条件分别解答,按第一个解答计分.
17.(15分
已知椭圆 的离心率为 ,点 中恰有两个点在
上.
(1)求 的方程;
(2)设 的内角 的对边分别为 ,
.若点 在 轴上且关于原点对称,问:是否存在
,使得点 都在 上,若存在,请求出 ,若不存在,请说明理由.
18.(17分)
某汽车厂商生产某型号具有自动驾驶功能的汽车,该型号汽车配备两个相互独立的自动驾驶系统(记为系
统 和系统 ),该型号汽车启动自动驾驶功能后,先启动这两个自动驾驶系统中的一个,若一个出现故
障则自动切换到另一个系统.为了确定先启动哪一个系统,进行如下试验:每一轮对系统 和 分别进行
测试试验,一轮的测试结果得出后,再安排下一轮试验.当一个系统出现故障的次数比另一个系统少2次时,
就停止试验,并认为出现故障少的系统比另一个系统更稳定.为了方便描述问题,约定:对于每轮试验,若
系统 不出现故障且系统 出现故障,则系统 得1分,系统 得-1分;若系统 出现故障且系统 不
出现故障,则系统 得-1分,系统 得1分;若两个系统都不出现故障或都出现故障,则两个系统均得0
分.系统 出现故障的概率分别记为 和 ,一轮试验中系统 的得分为 分.
(1)求 的分布列;
(2)若系统 和 在试验开始时都赋予2分, 表示“系统 的累计得分为 时,最终
认为系统 比系统 更稳定”的概率,则 , ,其中
.现根据 的值来决定该型号汽车启动自动驾驶功能后先启
学科网(北京)股份有限公司动哪个系统,若 ,则先启动系统 ;若 ,则先启动系统 ;若 ,则随机启
动两个系统中的一个,且先启动系统 的概率为 .
①证明: ;
②若 ,由①可求得 ,求该型号汽车启动自动驾驶功能后无需自动切换到另
一个自动驾驶系统的概率.
19.(17分
设 ,函数 ,
的定义域都为 .
(1)求 和 的值域;
(2)用 表示 中的最大者,证明: ;
(3)记 的最大值为 ,求 的最小值.
福建省漳州市 2024 届高三毕业班第四次教学质量检测
数学参考答案及评分细则
评分说明:
1.本解答给出了一种或几种解法供参考,如果考生的解法与本解答不同,可根据试题的主要
考查内容比照评分标准制定相应的评分细则.
2.对计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和
难度,可视影响的程度决定后继部分的给分,但不得超过该部分正确解答应给分数的一半;
如果后继部分的解答有较严重的错误,就不再给分.
3.解答右端所注分数,表示考生正确做到这一步应得的累加分数.
4.只给整数分数.选择题和填空题不给中间分.
一、单项选择题:本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只
有一项是符合题目要求的
1.B 2.B 3.D 4.C 5.D 6.A 7.A 8.C
二、多项选择题:本大题共3小题,每小题6分,共18分,在每小题给出的四个选项中,有
学科网(北京)股份有限公司多个选项符合题目要求,全部选对的得6分,部分选对的得部分分,有选错的得0分
9.AB 10.BCD 11.ABC
三、填空题:本大题共3题,每小题5分,共15分.
12. (写对一个方程即可) 13. 14.
四、解答题:本大题共5小题,共77分,解答应写出文字说明,证明过程或演算步骤.
15.解:
(1)因为 成等差数列,所以 ,
又 ,所以 ①,
在 中,由余弦定理可得: ,
又 ,所以 ②,
由①②得 ,
所以 的面积 .
(2)因为 ,所以 ,
又因为 且 ,所以 ,
所以 ,
所以 ,所以 ,
所以 ,
又因为 ,所以 ,所以 ,所以 ,
所以 .
16.解法一:
学科网(北京)股份有限公司(1)证明:如图,取 的中点 ,连接 .
因为 为侧棱 的中点,
所以 ,
因为 平面 平面 ,
所以 平面 ,
因为 ,
所以 ,
所以四边形 为平行四边形,
所以 .
因为 平面 平面 ,
所以 平面 ,
因为 平面 ,
所以平面 平面 .
因为 平面 ,所以 平面 .
(2)如图,连接 ,
因为 ,所以
因为 是等边三角形, 为 的中点,
所以 ,
因为平面 平面 ,
平面 平面 平面 ,
所以 平面 ,
学科网(北京)股份有限公司又 平面 ,所以 .
以 为原点, 所在直线为 轴, 所在直线为 轴, 所在直线为 轴,建立空间直角坐标系
,则
,
,
选择①:设 ,
由 ,
其中 为点 到平面 的距离,得 ,
又因为点 到平面 的距离 ,
所以 ,所以 ,
所以 ,
设平面 的法向量为 ,
则
取 ,得 ,
又 是平面 的一个法向量,
所以平面 与平面 所成角的余弦值为 .
选择②:设 ,
学科网(北京)股份有限公司因为 平面 ,所以 平面 ,
所以点 到平面 的距离为 ,
又点 到平面 的距离为 ,
所以 ,所以 ,所以 ,
以下同选择①
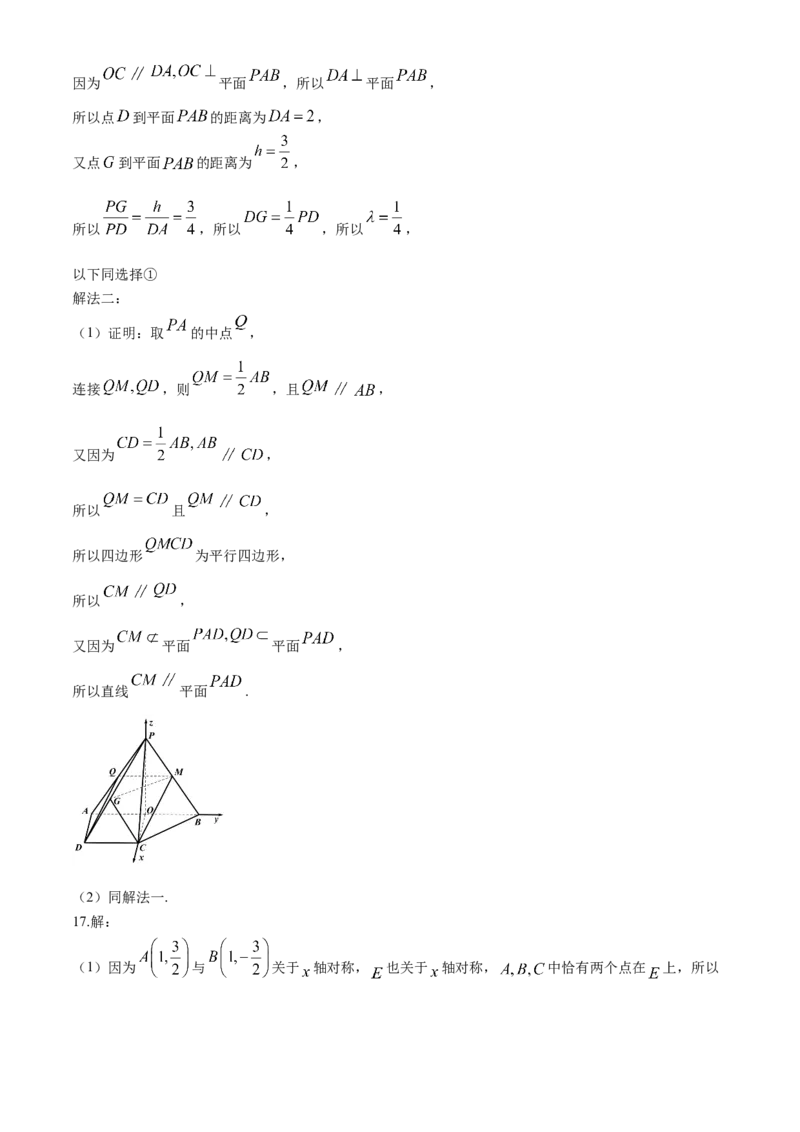
解法二:
(1)证明:取 的中点 ,
连接 ,则 ,且 ,
又因为 ,
所以 且 ,
所以四边形 为平行四边形,
所以 ,
又因为 平面 平面 ,
所以直线 平面 .
(2)同解法一.
17.解:
(1)因为 与 关于 轴对称, 也关于 轴对称, 中恰有两个点在 上,所以
学科网(北京)股份有限公司在 上, 不在 上,
所以 ,
又因为 ,
所以 ,
所以 的方程为 .
(2)存在 ,使得点 都在 上.理由如下:
因为 ,所以 ,
因为 ,
所以 ,即 ,
所以 ,
又因为 ,所以 ,
所以 ,即 ,
所以 ,
所以点 在以 为焦点, 为长轴长的椭圆上,
又因为 的焦点为 ,长轴长为4,点 在 轴上且关于原点对称,
所以点 都在椭圆 上 ,
所以存在 ,使得点 都在 上.
18.解法一:
学科网(北京)股份有限公司(1) 的所有可能取值为 .
,
,
所以 的分布列为
-1 0 1
(2)①由题意,
得 ,所以
所以 ,
又 ,
所以
所以
学科网(北京)股份有限公司,
所以 ,
②记“该型号汽车启动自动驾驶功能后无需自动切换到另一个自动驾驶系统”为事件 ,“该型号汽车启
动自动驾驶功能后先启动系统 ”为事件 ,
因为 ,
所以由题意,得 ,
,
所以
,
即该型号汽车启动自动驾驶功能后无需自动切换到另一个自动驾驶系统的概率为0.9988.
解法二:
(1)同解法一.
(2)①由题意,得 ,
又 ,
所以 ,所以
因为 ,所以 ,所以 ,
所以 ,
所以 ,所以 ,
学科网(北京)股份有限公司又因为 ,
所以 .
②同解法一.
19.解:
(1) ,
因为当 时, ;当 时, ,
所以 在 上单调递减,在 上单调递增,
又 ,
所以 的值域为 ,即 .
因为 是减函数,
所以 的值域为 ,即 .
(2)证明:当 时, ,即 ,
从而
当 时, ,即 ,
从而 ,
所以 ,
所以 .
.
学科网(北京)股份有限公司(3)由(1),得 ,
,
再结合(2),得
,
所以 ,
所以
,
又当 ,
,
(可取 )时, ,
所以 的最小值为 .
学科网(北京)股份有限公司