第22套：2024年2月“鸽子杯”数学试题(1)_2024年4月_01按日期_6号_2024届新结构高考数学合集_新高考19题（九省联考模式）数学合集140套_2024年2月“鸽子杯”数学

2024 年 2 月“鸽子杯”线上测试 数 学 注意事项： 1. 答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。 2. 回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。 如需改动，用橡皮擦干净后，再选涂其他答案标号。回答非选择题时，将答案写在答题 卡上，写在本试卷上无效。 3. 考试结束后，将本试卷和答题卡一并交回。 一、选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只 有一项是符合题目要求的。 1 1 1. 幂函数yx的图像经过( , )，则 4 2 1 1 A.  B. C. 2 D. 2 2 2 2. 若由最小二乘法得到的回归直线y x1，则其均值点可能是 A. (0,1) B. (1,0) C. (2,4) D. (3,7) 3. 已知集合A{1,2,m}，B{3,m2}，若AB，则满足条件的m有 A.3个 B.4个 C.5个 D.6个 4. 已知函数 f(x)2sin(x)是奇函数，则 f() A. 0 B. 1 C. 2 D. 2 5. 设A，B，C 是三个事件，则对事件“A，B不同时发生且B，C 有且只有一个发 生”的表示中，正确的是 A. ABC B. ABC ABC C. ABC ABC ABC D. ABC ABC  ABC ABC 6. 设无穷整数数列{a }的前n项和为S ，且有S2 2a ，则a  n n n n 2024 A. 2 B. 1 C. 1 D. 2 xlnx 7. 函数 f(x) 的两个极值点对应的函数点均在直线l上，则l的方程为 x2 1 1 A. y x B. yx C. y x D. y x 2 2 数学试题 第 1 页（共 4 页）8. 已知动点P在圆x2  y2 1上，定点Q的坐标为(1,1)，动点T 满足OT OPOQ， 其中，0，2 22 4，则QT 的最大值为 A. 2 2 B. 2 C. 2 D. 2 2 二、选择题：本题共3小题，每小题6分，共18分。在每小题给出的四个选项中，有 多项符合题目要求。全部选对的得6分，部分选对的得部分分，有选错的得0分。 9. 设复数z 34i与z 43i在复平面对应的点分别为P，Q，平面坐标原点为O， 1 2 则 1 2 z A. z z  PQ B. z z  PQ C. z z  OQ D. 1  OQ 2 1 2 1 2 1 2 z 2 10. 已知椭圆C ，双曲线C 有相同的焦点F ，F ，焦距为2，且C ，C 离心率互为倒 1 2 1 2 1 2 数. 记A ，A 分别为C ，C 的两个顶点，C ，C 有公共点P，且有 AF  AF ， 1 2 1 2 1 2 1 1 1 2 A F  A F ， PF  PF ，则 2 1 2 2 1 2 A. AA  PF B. AA  PF C. FPF P D. 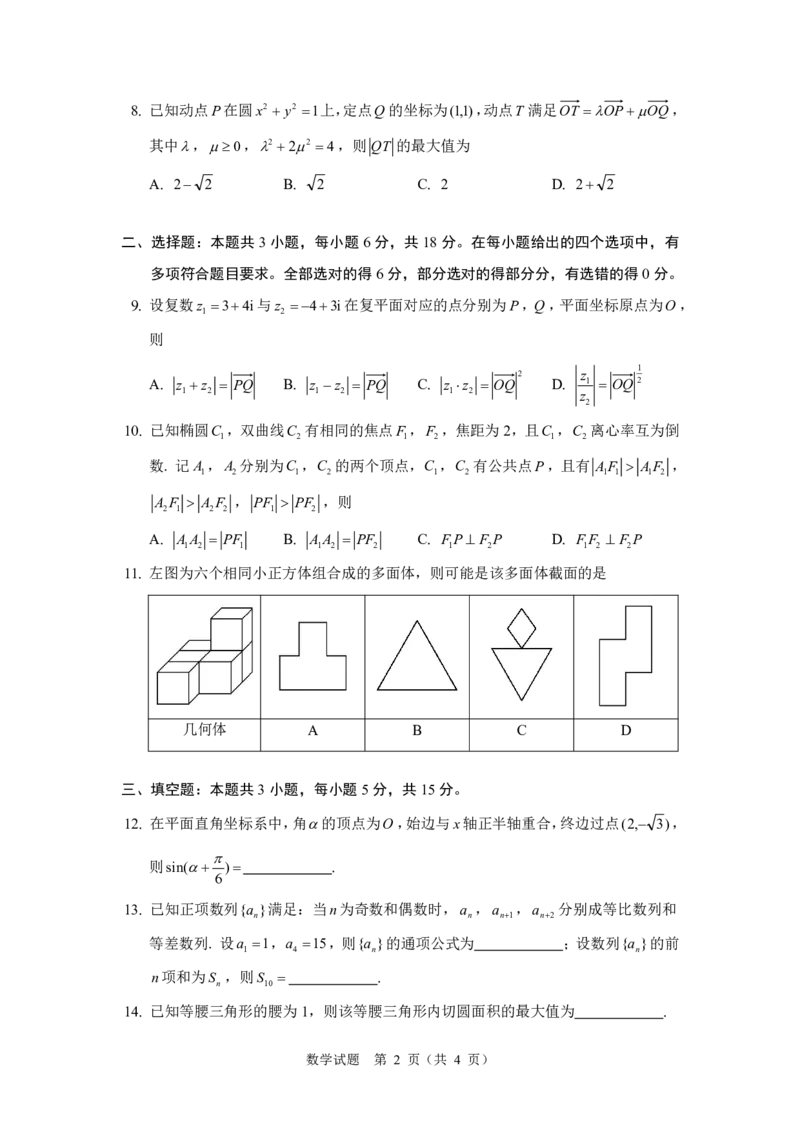FF F P 1 2 1 1 2 2 1 2 1 2 2 11. 左图为六个相同小正方体组合成的多面体，则可能是该多面体截面的是 几何体 A B C D 三、填空题：本题共3小题，每小题5分，共15分。 12. 在平面直角坐标系中，角的顶点为O，始边与x轴正半轴重合，终边过点(2, 3)，  则sin( ) . 6 13. 已知正项数列{a }满足：当n为奇数和偶数时，a ，a ，a 分别成等比数列和 n n n1 n2 等差数列. 设a 1，a 15，则{a }的通项公式为 ；设数列{a }的前 1 4 n n n项和为S ，则S  . n 10 14. 已知等腰三角形的腰为1，则该等腰三角形内切圆面积的最大值为 . 数学试题 第 2 页（共 4 页）四、解答题：本题共5小题，共77分。解答应写出文字说明、证明过程或演算步骤。 15.（13分） 某老师在课堂测验上设置了一种新的大题题型，这种大题题型由一个题干和五个与 题干有关的判断题组成，得分规则是：五道题中，全部正确判断则该大题得5分，有一 道错误判断则该大题得3分，有两道错误判断则该大题得1分，有三道及以上错误判断 则该大题不得分. 假定随机判断时，每道题正确判断和错误判断的概率相等. （1）若考生所有题目都随机判断，求此时得分的分布列和数学期望； （2）若考生能够正确判断其中两道题目，其余题目随机判断，求此时得分的数学 期望. 16.（15分） 请从以下三个条件中选择一个条件加入题干并完成求解，不同条件对应的本题满分 不同，若选择多个条件进行求解，将以分值较大的解答作为评分依据： 甲（满分10分）：BAC 60，PBPC； 乙（满分12分）：PA 2PB，△ABC的面积为10 3； 33 丙（满分15分）：点P到平面ABC的距离为 ，PA 2 5. 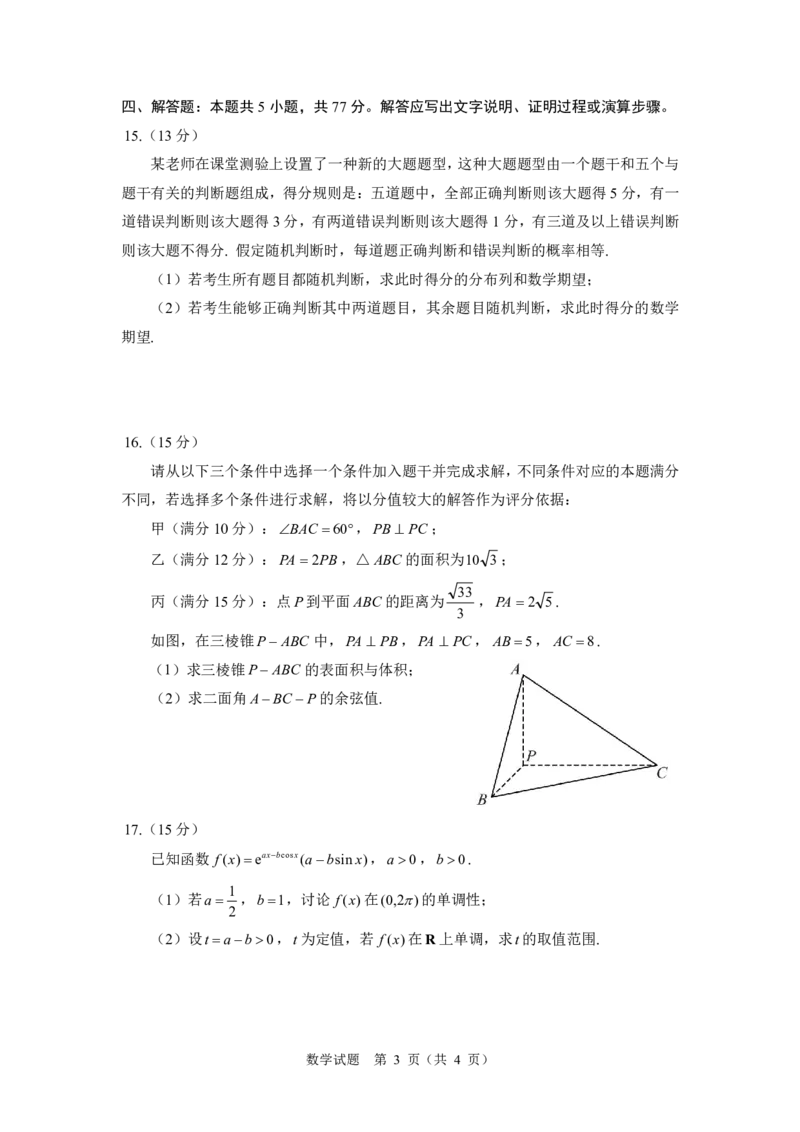3 如图，在三棱锥PABC 中，PA PB，PA PC，AB5，AC 8. （1）求三棱锥PABC 的表面积与体积； （2）求二面角ABCP的余弦值. 17.（15分） 已知函数 f(x)eaxbcosx(absinx)，a0，b0. 1 （1）若a ，b1，讨论 f(x)在(0,2)的单调性； 2 （2）设t ab0，t为定值，若 f(x)在R上单调，求t的取值范围. 数学试题 第 3 页（共 4 页）18.（17分） 循环排列（也称圆排列）是指从n个不同元素中取出m个不同的元素排成一个环形， 既无头也无尾. 循环排列视所有循环的情形为同一种排列，例如123、231、312在循环 排列中便视为一种排列；同时将顺时针和逆时针视为两种循环排列，例如123和132便 是两种不同的循环排列.（本题中，m，n均为正整数，且mn） （1）若从n个人中选择m个人围坐成一个圆桌，直接写出这样的排列个数； （2）定义：将n个不同元素划分成m个非空循环排列（即每个排列中都有至少一 个元素），所有这样的排列的个数用符号s(n,m)表示. 并规定s(0,0)1，s(n,0)0. ①求s(4,2)； ②证明：s(n,m)ns(n,m1)s(n1,m1)，其中mn； （3）已知某饭店有n张圆桌，每张圆桌最多可以容纳n个人，最少可以不坐人. 现 在有n个人来到饭店就餐，若将每张桌上围坐多人时不同的循环排列视为不同方案，将 相同循环排列坐在不同桌视为同种方案，求总的方案数. 19.（17分） 在平面直角坐标系xOy中有定点F( 2,0)，F ( 2,0)，动点P满足：点P到y轴 1 2 2 的距离与点P到F ，F 距离之和的比值为 . 1 2 4 （1）求点P轨迹的方程； （2）设点Q为上一点， PQ 4，求△PQF 面积的最大值. 1 数学试题 第 4 页（共 4 页）18.（17分） 在平面直角坐标系xOy中有定点F( 2,0)，F ( 2,0)，动点P满足：点P到y轴 1 2 2 的距离与点P到F ，F 距离之和的比值为 . 1 2 4 （1）求点P轨迹的方程； （2）设点Q为上一点， PQ 4，求△PQF 面积的最大值. 1 19.（17分） 循环排列（也称圆排列）是指从n个不同元素中取出m个不同的元素排成一个环形， 既无头也无尾. 循环排列视所有循环的情形为同一种排列，例如123、231、312在循环 排列中便视为一种排列；同时将顺时针和逆时针视为两种循环排列，例如123和132便 是两种不同的循环排列.（本题中，m，n均为正整数，且mn） （1）若从n个人中选择m个人围坐成一个圆桌，直接写出这样的排列个数； （2）定义：将n个不同元素划分成m个非空循环排列（即每个排列中都有至少一 个元素），所有这样的排列的个数用符号s(n,m)表示. 并规定s(0,0)1，s(n,0)0. ①求s(4,2)； ②证明：(n1)s(n,m)s(n,m1)s(n1,m1)，其中mn； （3）已知某饭店有n张圆桌，每张圆桌最多可以容纳n个人，最少可以不坐人. 现 在有n个人来到饭店就餐，若将每张桌上坐多人时不同的循环排列视为不同方案，求总 的方案数. 数学试题 第 4 页（共 4 页）