文档内容
2025年普通高等学校招生全国统一考试模拟测试(二)
数学 参考答案
一、单项选择题
题号 1 2 3 4 5 6 7 8
答案 D C A B C B A D
二、多项选择题
题号 9 10 11
答案 BC BCD ACD
三、填空题
12. 13. 14. ,
四、解答题
15.解:(1)由余弦定理得 ,···················································2分
所以 ,····································································4分
(没变形但答案正确不扣分)
所以 .········································································································6分
(2)由正弦定理得 ,······················7分
整理得 ,··································8分
(正弦定理与正弦二倍角公式各1分)
因为 ,所以 ,···9分
所以 ,··············································································10分
(化简最后结果正确即可得分)
高三数学 第1页(共9页)因为 ,所以 ,解得 ,···············································11分
所以 ,·····························································································12分
( 与 都没有扣1分)
所以 .································································13分
(答案正确,面积公式没写不扣分)
16. 解:(1)由已知得 ,································································1分
设点 ,则 ,且 ,所以 ,
·······················································································································2分
因为 ,所以 ,············································3分
因为 ,所以 ,所以 .··········································5分
另解:因为 ,所以 ,·································3分
因为 ,所以 ,所以 . ··································5分
(x范围写错,但题目过程思路正确,给3分)
(2)解法一:
假设四边形 是以 为对称轴的,
则 ,且 的中点 在 上,···································································6分
设 , ,则 , ,
,···················································································7分
高三数学 第2页(共9页)(说明M是AC中点,且写出中点坐标关系即可得分)
所以 ,····················································································8分
因为点 在第一象限,且 ,所以 ,····················································9分
所以 ,·········································································10分
所以 ,············································································11分
因为 三点共线,所以 ,·························································12分
所以 ,···········································································13分
因为 ,与 矛盾,故假设不成立,···················································14分
所以四边形 不能是以 为对称轴································································15分
解法二:
假设四边形 是以 为对称轴的,
则 ,且 的中点 在 上,································································6分
因为点 在第一象限,所以直线 斜率存在且直线 不过原点,·····························7分
设直线 的方程为 ,···························································8分
联立得 ,消去 并整理得 ,·························5分
(注:设直线AC方程时,没有说明k存在,扣1分)
设 ,则 ········································10分
所以 的中点为 ,································································11分
高三数学 第3页(共9页)因为 三点共线,所以 ,·······················································12分
所以 ,············································································13分
因为 ,与 矛盾,故假设不成立,···················································14分
所以四边形 不能是以 为对称轴································································15分
另解:
因为 ,所以 ,则直线OB方程为: ································12分
因为 的中点 在 上,所以 代入直线OB方程得:
,解得m=0,即直线AC过原点O·······································14分
所以A、O、C三点共线,与OABC为四边形矛盾,
所以四边形 不能是以 为对称轴································································15分
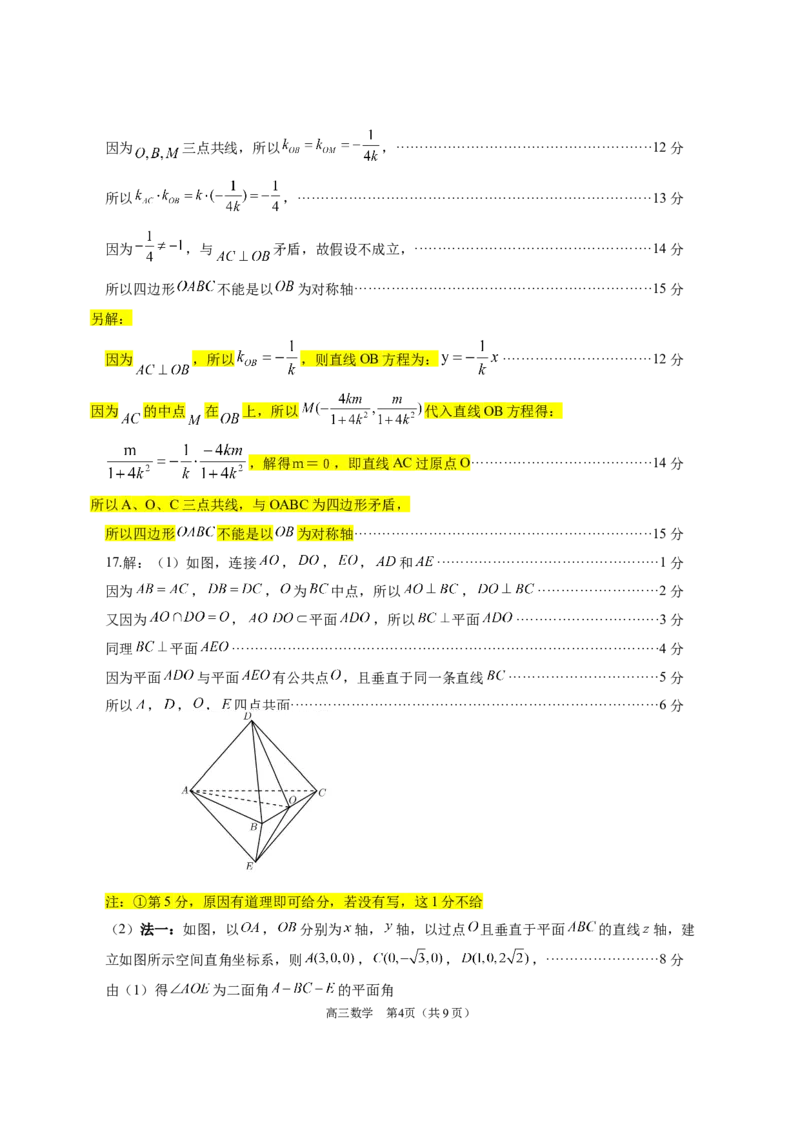
17.解:(1)如图,连接 , , , 和 ················································1分
因为 , , 为 中点,所以 , ··························2分
又因为 , 平面 ,所以 平面 ·······························3分
同理 平面 ····························································································4分
因为平面 与平面 有公共点 ,且垂直于同一条直线 ································5分
所以 , , , 四点共面···············································································6分
注:①第5分,原因有道理即可给分,若没有写,这1分不给
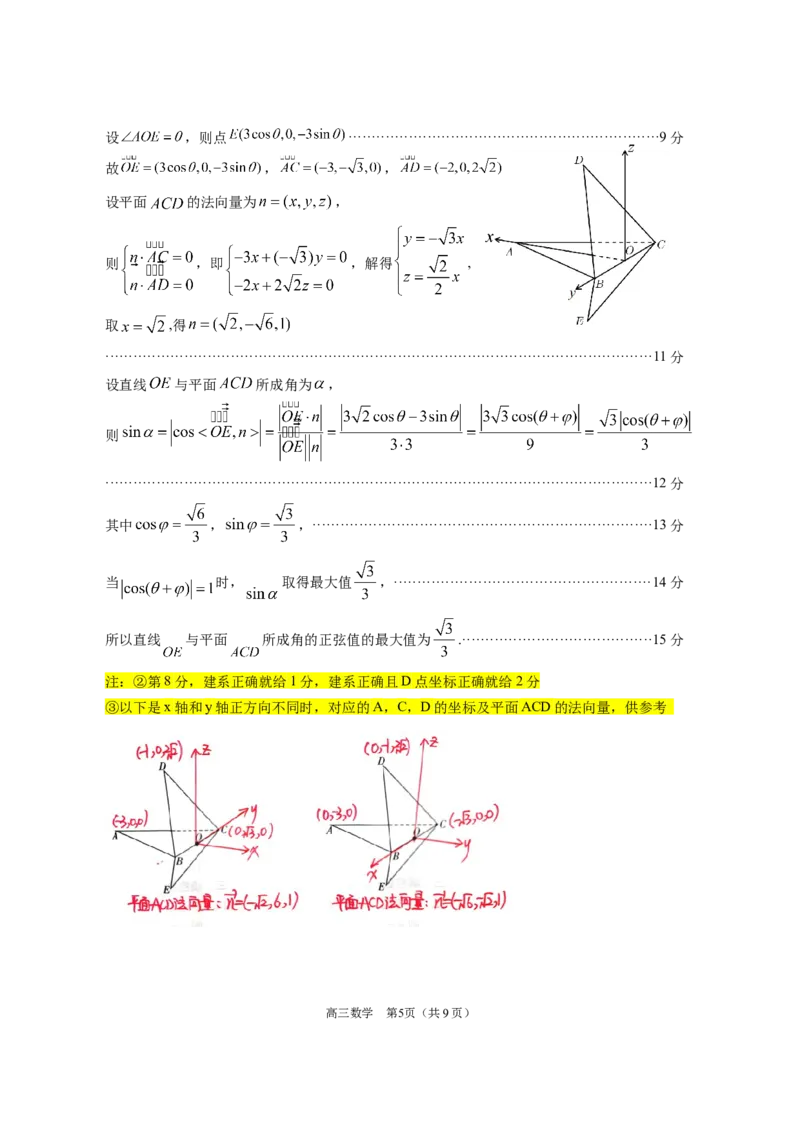
(2)法一:如图,以 , 分别为 轴, 轴,以过点 且垂直于平面 的直线 轴,建
立如图所示空间直角坐标系,则 , , ,························8分
由(1)得 为二面角 的平面角
高三数学 第4页(共9页)设 ,则点 ···································································9分
故 , , ,
设平面 的法向量为 ,
则 ,即 ,解得 ,
取 ,得
······················································································································11分
设直线 与平面 所成角为 ,
则
······················································································································12分
其中 , ,·········································································13分
当 时, 取得最大值 ,·······················································14分
所以直线 与平面 所成角的正弦值的最大值为 .·········································15分
注:②第8分,建系正确就给1分,建系正确且D点坐标正确就给2分
③以下是x轴和y轴正方向不同时,对应的A,C,D的坐标及平面ACD的法向量,供参考
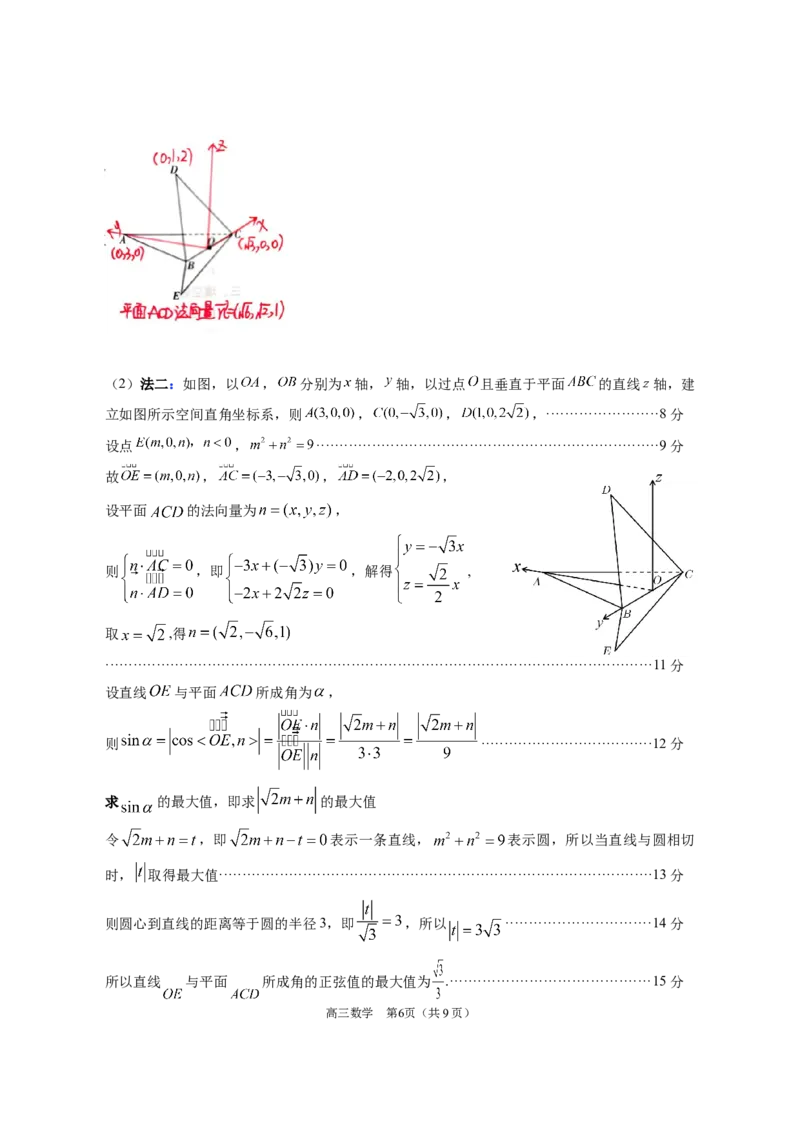
高三数学 第5页(共9页)(2)法二:如图,以 , 分别为 轴, 轴,以过点 且垂直于平面 的直线 轴,建
立如图所示空间直角坐标系,则 , , ,························8分
设点 , ··········································································9分
故 , , ,
设平面 的法向量为 ,
则 ,即 ,解得 ,
取 ,得
······················································································································11分
设直线 与平面 所成角为 ,
则 ·····································12分
求 的最大值,即求 的最大值
令 ,即 表示一条直线, 表示圆,所以当直线与圆相切
时, 取得最大值·····························································································13分
则圆心到直线的距离等于圆的半径3,即 ,所以 ·······························14分
所以直线 与平面 所成角的正弦值的最大值为 .···········································15分
高三数学 第6页(共9页)18. 解:(1)质点运动3次后停在原点右侧的情况有4种,分别是:0次不动、3次向右、0次
向左;1次不动、2次向右、0次向左;0次不动、2次向右、1次向左;2次不动、1次向右、0
次向左.·············································································································2分
所以质点运动3次后停在原点右侧的概率
.·····································4分
说明:每1种情况分析、列式正确得1分.
(分类不完整,每少一种情况扣2分;分类完整,概率计算错误扣1分)
(2)①质点在运动过程中出现在原点左侧就停止运动且运动5次后停在原点右侧的情况有4
种:5次向右;第1次向右、后4次有3次向右1次向左;前2次向右、后3次有1次向右2次
向左;第1次向右、第2次向左、第3次向右、后2次有1次向右1次向左.····················6分
所以质点在运动过程中出现在原点左侧就停止运动且运动5次后停在原点右侧的概率
.································································································8分
说明:每1种情况分析、列式正确得1分.
(分类不完整,每少一种情况扣2分;分类完整,概率计算错误扣1分)
②第一轮游戏结束进入第二轮游戏的情况有2种,分别是3次向右;2次向右,1次向左.
其概率为 ;····································································9分
设两轮游戏最终得分的随机变量为 ,则 的所有可能取值为0,1,3,
易知 的期望 仅与 1,3的概率只有关,因此
,
,·············································································10分
所以最终得分 的期望
高三数学 第7页(共9页),···········11分
(计算每个概率时未乘 ,给1分)
因为 ,所以 ,即 ,
所以当 时, ;当 时, ;·······································12分
记 ,
求导得
记 ,··············································································13分
解法一、①当 时, ,
因为 , , ,
所以由零点存在定理,存在 ,使得 ;存在 ,使得 ,
当 时, ;当 时, ,
所以 在 上单调递增,在 上单调递减,
所以 是 的极大值点,
所以 .····································································································15分
②当 时, ,
因为 , , ,
所以由零点存在定理,存在 ,使得 ;存在 ,使得 ,
若要使得 在 上存在极大值点,
则 ,
高三数学 第8页(共9页)解得 或 ,
因为 ,所以 .
综上所述 .······················································································17分
解法二、令 ,得 ,
令 , ,
①当 时, , , , ,易得 在 上
单调递增, ,
(ⅰ)当 时,当 时, ,由极大值点的定义判断,函数 在 上
存在唯一极大值点;
(ⅱ)当 时, ,
,当 时, 恒成立,即
,由极大值点的定义判断,函数 在 上存在唯一极大值点;
所以 .····································································································15分
②当 时, , , , ,易得 在 上
单调递增,
当 时, ,由极大值点的定义判断,只需 即可,即
高三数学 第9页(共9页),解得解得 或 ,因为 ,所以 .
综上所述 .······················································································17分
(①②两种情况中,未区分当 时, ;当 时, 两种情况,对
进行分析,酌情给1-2分)
19.解:(1)由题意得 , ,·······························2分
( 与 每算对一个给1分)
所以 , .····························································································4分
( 与 每算对一个给1分)
(2)由题得 ,
所以 .···················5分
因此 中的数对 必由 中的数对 经运算 得到, 中的数对
必由 中的 或数对 经运算 得到,··························································6分
(能说明“要产生 ,必需 ,要产生 ,则需要 或 给2分)
因为 是 数组,其中有一半的项为0,即 个0,经过两次运算 能在 中产生
个数对 ,·································································································7分
因为 中数对 的个数为 个,经过两次运算 能在 中产生 个数对 ,
高三数学 第10页(共9页)·······················································································································8分
所以 ,即 ,··································································9分
所以 ,(少此步扣1分)
所以数列 是以2为首项,2为公比的等比数列.··········································10分
(3)当 为奇数时, ,累加得
因为 ,所以 ( 为奇数).···························································11分
当 为偶数时, ,累加得
因为 ,所以 ( 为偶数).···········································12分
所以 ,
故 . ·······································································13分
(
高三数学 第11页(共9页)或 均得1分)
因 为 当 且 为 偶 数 时 ,
.
······················································································································14分
①当 时, ;···············································································15分
②当 且 为奇数时,
;····················16分
③当 且 为偶数时,因为对任意的 都有 ,所以
;
综上所述,对任意的 都有 .·······························17分
高三数学 第12页(共9页)