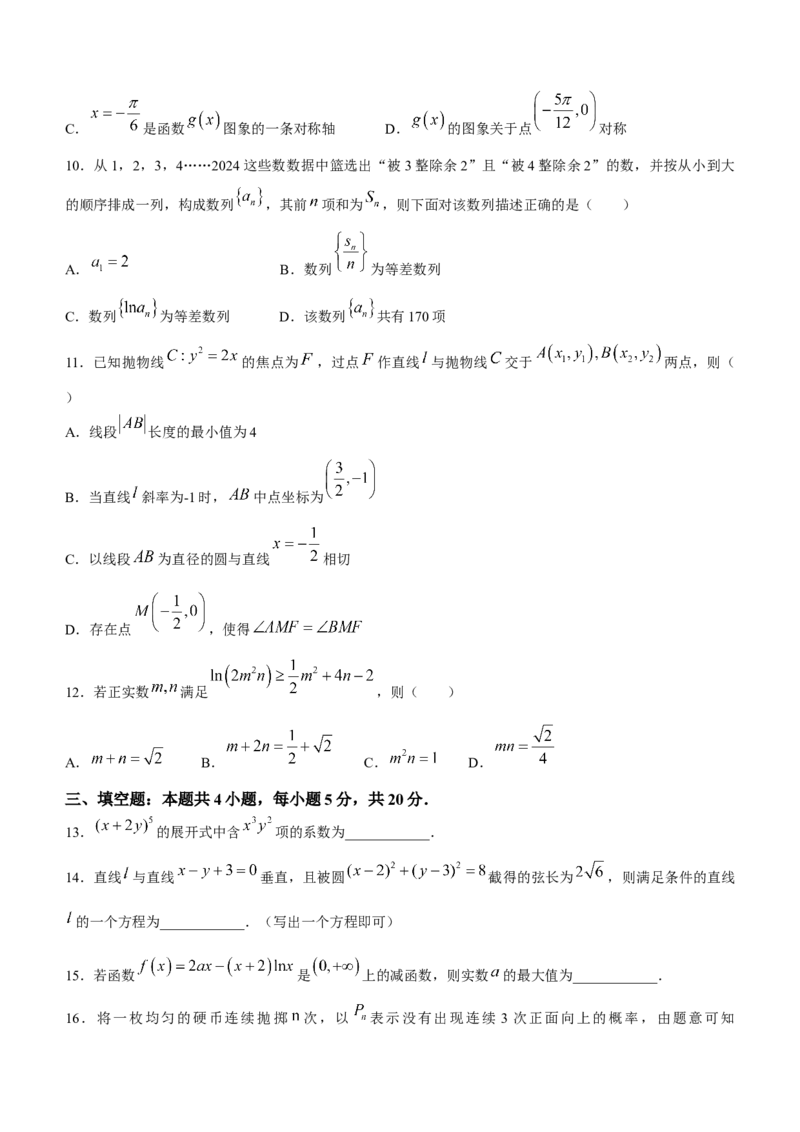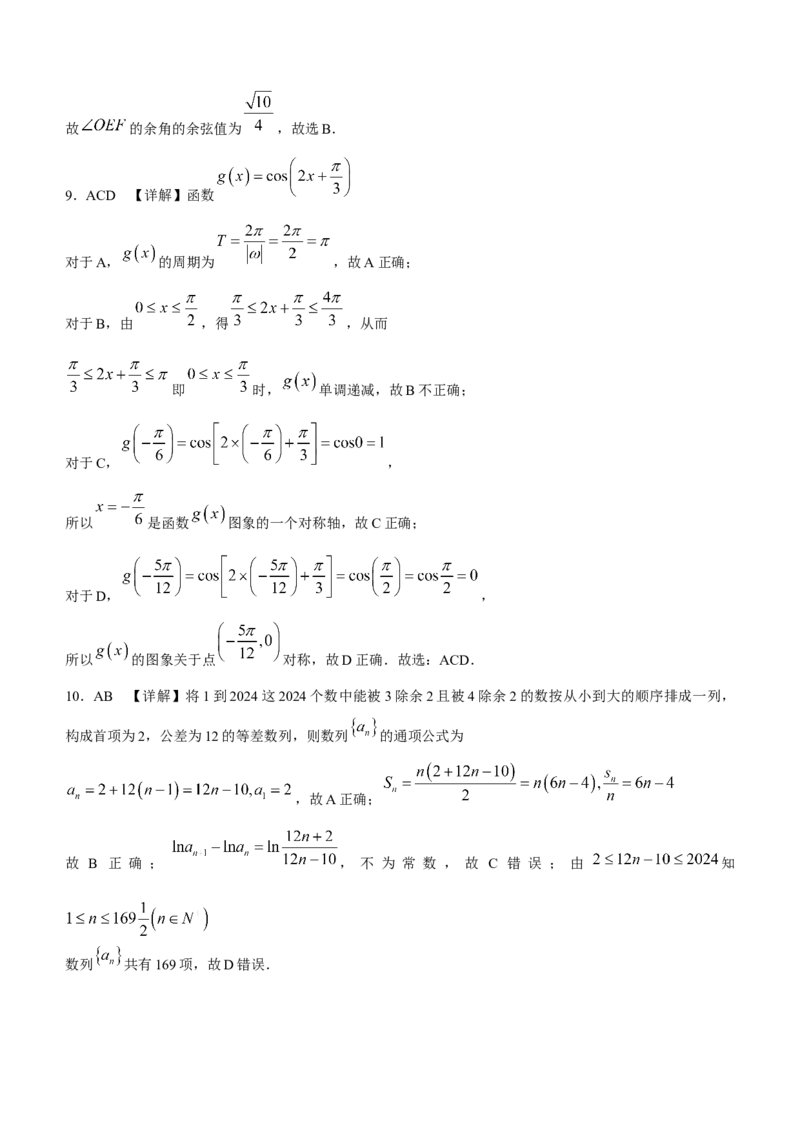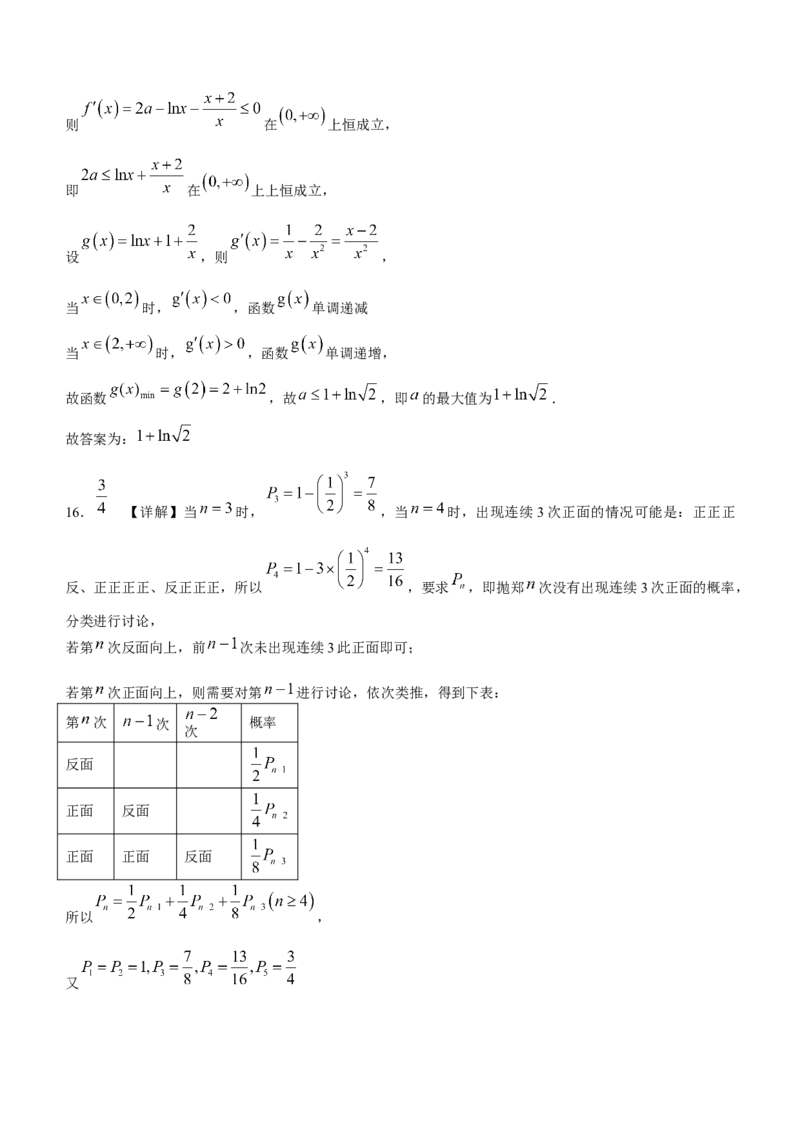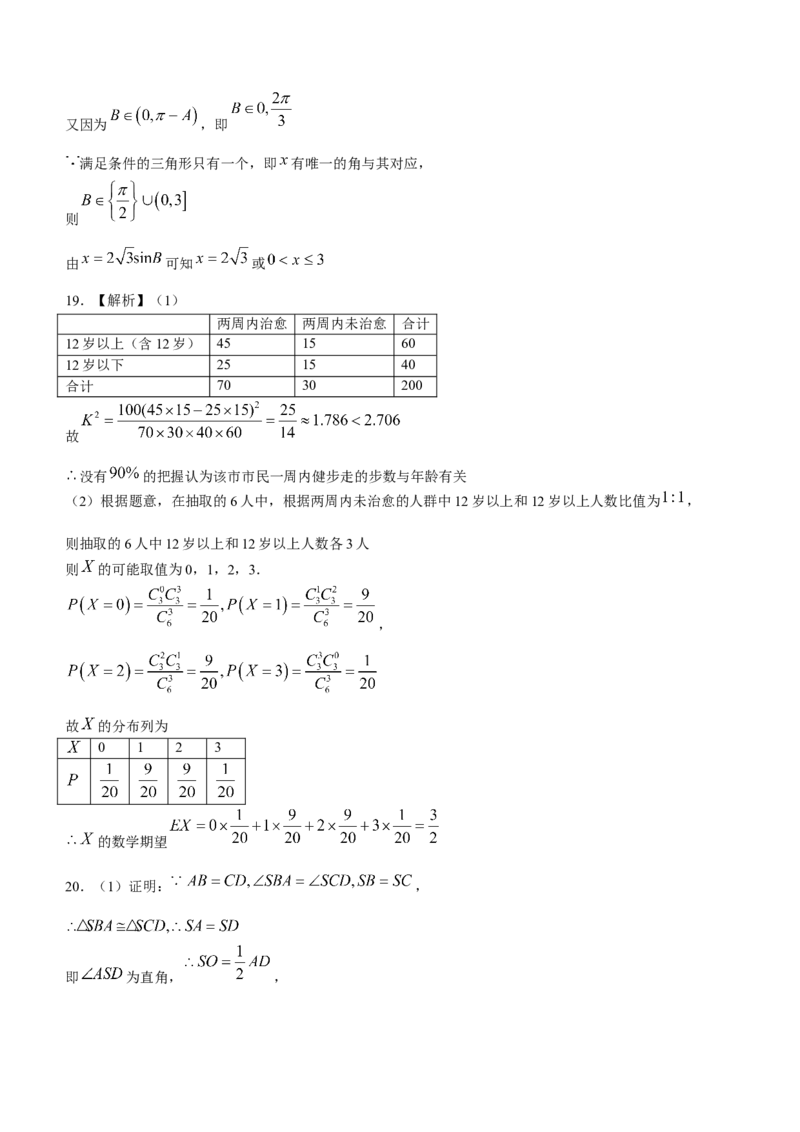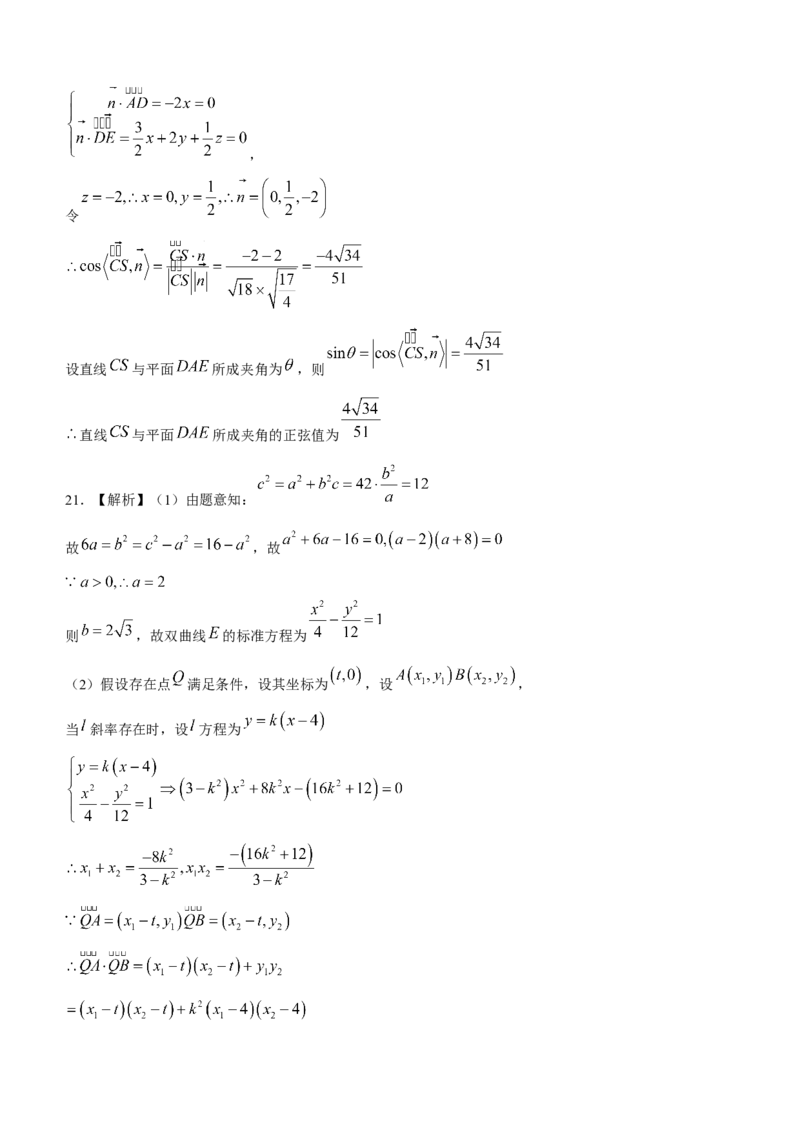文档内容
2023 年广西三新学术联盟高三年级 11 月联考
数学
本卷满分:150分,考试时间:120分钟.
注意事项:
1.答题前、考生先在答题卡上用直径05毫米黑色墨水签字笔将自己的姓名、学校、班级、准
考证号填写清楚,然后贴好条形码.清认真核准条形码上的准考证号、姓名和科目.
2.答选择题时、选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动、
用橡皮擦干净,再选涂其他答案标号,回答非选择题时,请用直径 0.5毫米黑色墨水签字笔在
答题卡上各题的答题区域内作答,在试题卷上作答无效.
一、选择题:本题共8小题,每小题5分,共40分,在每小题给出的四个逃项中,只有一项是
符合题目要求的.
1.已知集合 ,则 ( )
A. B. C. D.
2.若 (其中 为虚数单位),则 ( )
A.1 B.2 C.3 D.4
3.为了得到函数 的图像,只需要将函数 的图像( )
A.向左平移 个单位 B.向右平移 个单位
C.向左平移 个单位 D.向右平移 个单位
4.已知向量 ,若向量 与 垂直,则实数 的值为( )
A. B.1 C. 或1 D.
5.北京时间2023年10月31日8时11分,神舟十六号载人飞船返回舱在东风着陆场成功着陆,载人飞行任
务取得圆满成功.某高中学校在有120名同学的“航天”社团中随机抽取24名参加一个交流会,若按社团中
高一、高二、高三年级的成员人数比例分层随机抽样,则高一年级抽取 6人,若按性别比例分层随机抽样,
则女生抽取15人,则下列结论错误的是( )
A.24是样本容量
B.120名社团成员中男生有50人
学科网(北京)股份有限公司C.高二与高三年级的社团成员共有90人
D.高一年级的社团成员中女生最多有30人
6.科技是一个国家强盛之根,创新是一个民族进步之魂,科技创新铸就国之重器.由中国科学院空天信息创
新研究院自主研发的极目一号Ⅲ型浮空艇(如图1)从海拔4300米的中国科学院珠穆朗玛峰大气与环境综合
观测研究站附近发放场地升空,最终超过珠峰8848.86米的高度,创造了海拔9032米的大气科学观测海拔高
度世界纪录,彰显了中国实力.“极目一号”Ⅲ型浮空艇长45米,高16米,若将它近似看作一个半球、一
个圆柱和一个圆台的组合体,正视图如图2所示,则“极目一号”Ⅲ型浮空艇的表面积为( )
图1 图2
A. B. C. D.
7 . 已 知 是 椭 圆 的 右 焦 点 , 点 在 椭 圆 上 , 线 段 与 圆
相切于点 ,且 ,则椭圆 的离心率等于( )
A. B. C. D.
8.已知 是体积为 的球体表面上的四点, ,则平面
与平面 的夹角的余弦值为( )
A. B. C. D.
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目
要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9.已知函数 ,则下列说法正确的是( )
A. 的最小正周期为 B. 在区间 上单调递减
学科网(北京)股份有限公司C. 是函数 图象的一条对称轴 D. 的图象关于点 对称
10.从1,2,3,4……2024这些数数据中篮选出“被3整除余2”且“被4整除余2”的数,并按从小到大
的顺序排成一列,构成数列 ,其前 项和为 ,则下面对该数列描述正确的是( )
A. B.数列 为等差数列
C.数列 为等差数列 D.该数列 共有170项
11.已知抛物线 的焦点为 ,过点 作直线 与抛物线 交于 两点,则(
)
A.线段 长度的最小值为4
B.当直线 斜率为-1时, 中点坐标为
C.以线段 为直径的圆与直线 相切
D.存在点 ,使得
12.若正实数 满足 ,则( )
A. B. C. D.
三、填空题:本题共4小题,每小题5分,共20分.
13. 的展开式中含 项的系数为____________.
14.直线 与直线 垂直,且被圆 截得的弦长为 ,则满足条件的直线
的一个方程为____________.(写出一个方程即可)
15.若函数 是 上的减函数,则实数 的最大值为____________.
16.将一枚均匀的硬币连续抛掷 次,以 表示没有出现连续 3 次正面向上的概率,由题意可知
学科网(北京)股份有限公司,则 ____________.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(本题满分10分)已知 是数列 的前 项和,且满足 ,
(1)记 ,求证:数列 为等比数列;
(2)设 ,求数列 的前 项和
18.(本题满分12分)已知在 中,内角 所对的边分别为 ,已知
(1)若 ,求 周长的最大值
(2)若 ,满足此条件的三角形只有一个,求实数 的取值范围
19.(本题满分12分)某调查小组为了解本市不同年龄段的肺炎患者在肺炎确诊两周内的治疗情况,在肺炎
患者中随机抽取100人进行调查,并将调查结果整理如下:
两周内治愈 两周内未治愈
12岁以上(含12岁) 45 15
12岁以下 25 15
(1)试判断是否有 的把握认为该市肺炎患者在肺炎确诊两周内治愈与年龄有关;
(2)现从样本中肺炎确诊两周内未治愈的人群中用分层抽样法抽取 6人做进一步调查,然后从这6人中随机
抽取3人填写调查问卷,记这3人中12岁以下的人数为 ,求 的分布列与数学期望.
附:
0.150 0.100 0.050 0.025
2.072 2.706 3.841 5.024
,其中 .
20.(本题满分12分)如图:四棱雉 中,底面 为矩形, 为直角三角
形, 的面积是 面积的 倍.
学科网(北京)股份有限公司(1)求证:平面 平面 ;
(2) 为 上的一点,四棱雉 的体积为四棱雉 体积的一半,求直线 与平面
所成角的正弦值.
21.(本题满分12分)已知双曲线 的右焦点为 ,过 且与 轴垂直的
弦长为12.
(1)求双曲线 的标准方程;
(2)过 作直线 与双曲线交于 两点,问在 轴上是否存在点 ,使 为定值,若存在,请求
出 点坐标,若不存在,请说明理由.
22.(本题满分12分)已知函数 .
(1)当 时,求 的图象在 处的切线方程;
(2)若方程 有三个不同的根,求实数 的取值范围.
2023 年广西三新学术联盟高三年级 11 月联考
数学试题参考答案
1.D 【详解】 ,则 .故选D.
2.C 【详解】由 ,可得 ,解得 ,故选C.
3.A 【详解】因为 ,所以只需要将函数 的图像向左平
移 个单位,即可得到 的图象.
学科网(北京)股份有限公司4.C 【详解】由 与 垂直,可得 ,解得 或1,故选C.
5.B 【详解】对于A,由样本容量定义知:样本容量为24,A正确;
对于B, 女生共有 人, 男生有 人,B错误;
对于C, 高一年级的社团成员有 人, 高二高三年级的社团成员共有 人,C
正确;
对于D,由C知:高一年级的社团成员共30人, 高一年级的社团成员中女生最多有30人, 正确.故选:
B.
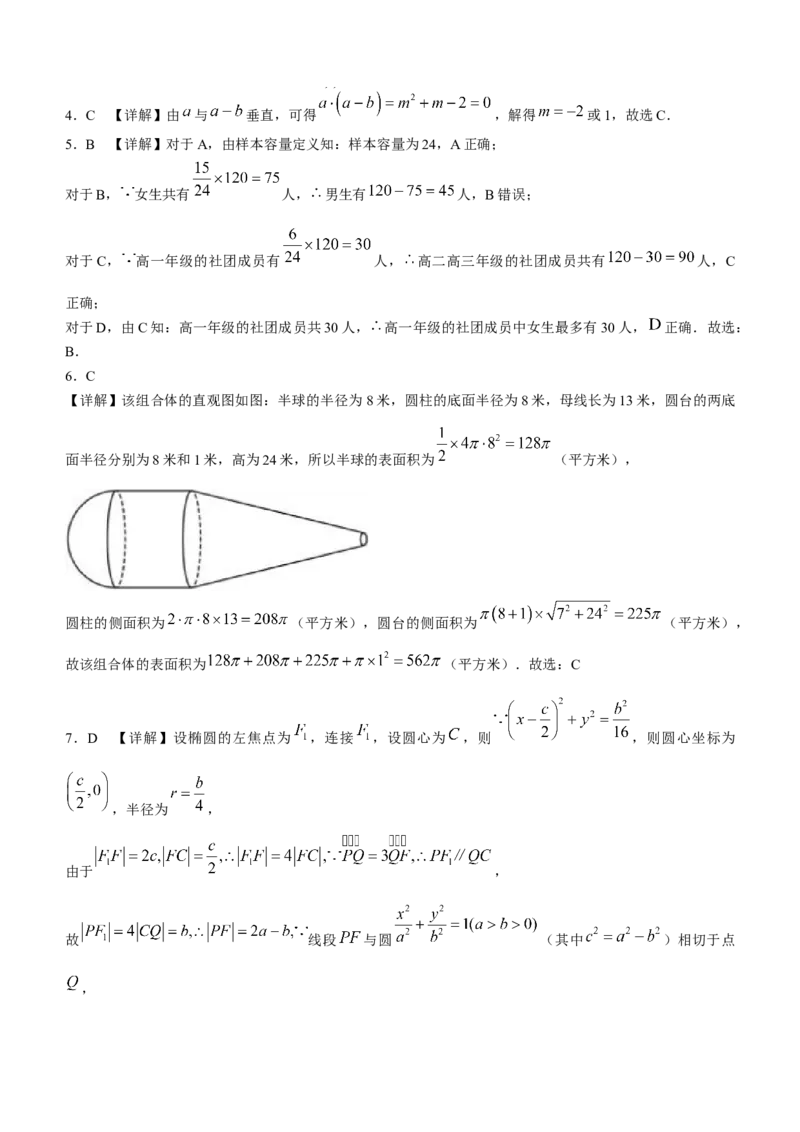
6.C
【详解】该组合体的直观图如图:半球的半径为8米,圆柱的底面半径为8米,母线长为13米,圆台的两底
面半径分别为8米和1米,高为24米,所以半球的表面积为 (平方米),
圆柱的侧面积为 (平方米),圆台的侧面积为 (平方米),
故该组合体的表面积为 (平方米).故选:C
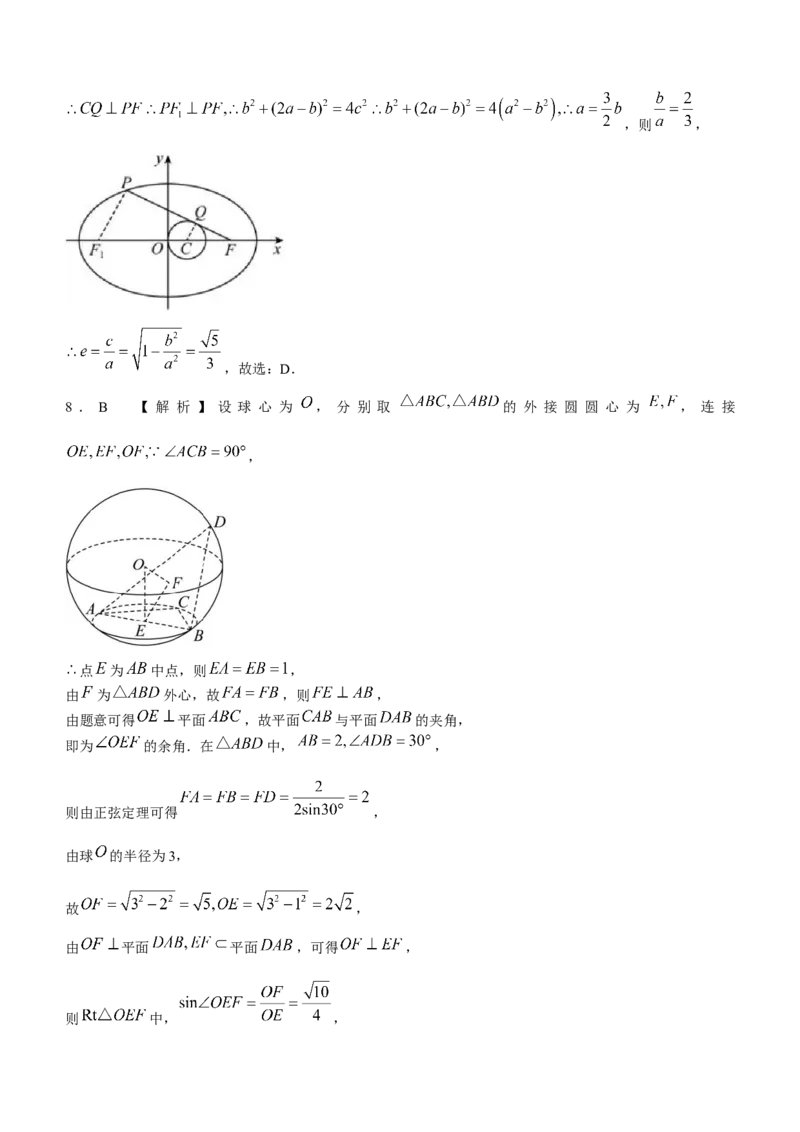
7.D 【详解】设椭圆的左焦点为 ,连接 ,设圆心为 ,则 ,则圆心坐标为
,半径为 ,
由于 ,
故 线段 与圆 (其中 )相切于点
,
学科网(北京)股份有限公司,则 ,
,故选:D.
8 . B 【 解 析 】 设 球 心 为 , 分 别 取 的 外 接 圆 圆 心 为 , 连 接
,
点 为 中点,则 ,
由 为 外心,故 ,则 ,
由题意可得 平面 ,故平面 与平面 的夹角,
即为 的余角.在 中, ,
则由正弦定理可得 ,
由球 的半径为3,
故 ,
由 平面 平面 ,可得 ,
则 中, ,
学科网(北京)股份有限公司故 的余角的余弦值为 ,故选B.
9.ACD 【详解】函数
对于A, 的周期为 ,故A正确;
对于B,由 ,得 ,从而
即 时, 单调递减,故B不正确;
对于C, ,
所以 是函数 图象的一个对称轴,故C正确;
对于D, ,
所以 的图象关于点 对称,故D正确.故选:ACD.
10.AB 【详解】将1到2024这2024个数中能被3除余2且被4除余2的数按从小到大的顺序排成一列,
构成首项为2,公差为12的等差数列,则数列 的通项公式为
,故A正确;
故 B 正 确 ; , 不 为 常 数 , 故 C 错 误 ; 由 知
数列 共有169项,故D错误.
学科网(北京)股份有限公司11.BCD 【解析】 为 ,通径最短,故 最短长度为 ,A错误;
此时直线 为 ,法一.与 联立得 ,
,故中点为 ,
法二.设中点坐标为 ,两式相减有 ,
故 ,故 ,B正确;
设 中点为 ,过点 作准线 的垂线,垂足分别为 ,
由抛物线定义知 ,
,
故以线段 为直径的圆与直线 相切,C正确;
设直线 为 ,与 联立得 ,
,
故 ,D正确
12.BD 【详解】依题意可知 ,
学科网(北京)股份有限公司不等式 可化为 ,
令 ,则 ,即 ,
设 ,
所以 在区间 递增;在区间 递减.
所以 ,所以要使 成立,则 ,
即 ,由于 ,故解得 ,
则 ,所以BD选项正确.
13.40 【详解】依题可得
14. (答案不唯一)
【详解】因为直线 与直线 垂直,可设 ,
由圆 ,可得圆心坐标为 ,半径为 ,
又因为弦长为 ,可得圆心到直线 的距离为 ,
即 ,解得 或 .
所以直线 的方程为 或 ,
故答案为: (或 .
15.
【详解】 是 上的减函数,
学科网(北京)股份有限公司则 在 上恒成立,
即 在 上上恒成立,
设 ,则 ,
当 时, ,函数 单调递减
当 时, ,函数 单调递增,
故函数 ,故 ,即 的最大值为 .
故答案为:
16. 【详解】当 时, ,当 时,出现连续3次正面的情况可能是:正正正
反、正正正正、反正正正,所以 ,要求 ,即抛郑 次没有出现连续3次正面的概率,
分类进行讨论,
若第 次反面向上,前 次未出现连续3此正面即可;
若第 次正面向上,则需要对第 进行讨论,依次类推,得到下表:
第 次 次 概率
次
反面
正面 反面
正面 正面 反面
所以 ,
又
学科网(北京)股份有限公司17.【答案】 (1)
当 时, ,解得 .
当 时, ,两式子相减得,
,即
可以得到 ,即
又 ,
数列 是一个以1为首项,2为公比的等比数列
(2)由(1)可知, ,而
故
18.(1) ,
得
由余弦定理得:
又因为
故
当且仅当 成立,周长最大值为9
(2)由正弦定理得 ,则有
学科网(北京)股份有限公司又因为 ,即
满足条件的三角形只有一个,即 有唯一的角与其对应,
则
由 可知 或
19.【解析】(1)
两周内治愈 两周内未治愈 合计
12岁以上(含12岁) 45 15 60
12岁以下 25 15 40
合计 70 30 200
故
没有 的把握认为该市市民一周内健步走的步数与年龄有关
(2)根据题意,在抽取的6人中,根据两周内未治愈的人群中12岁以上和12岁以上人数比值为 ,
则抽取的6人中12岁以上和12岁以上人数各3人
则 的可能取值为0,1,2,3.
,
故 的分布列为
0 1 2 3
的数学期望
20.(1)证明: ,
即 为直角, ,
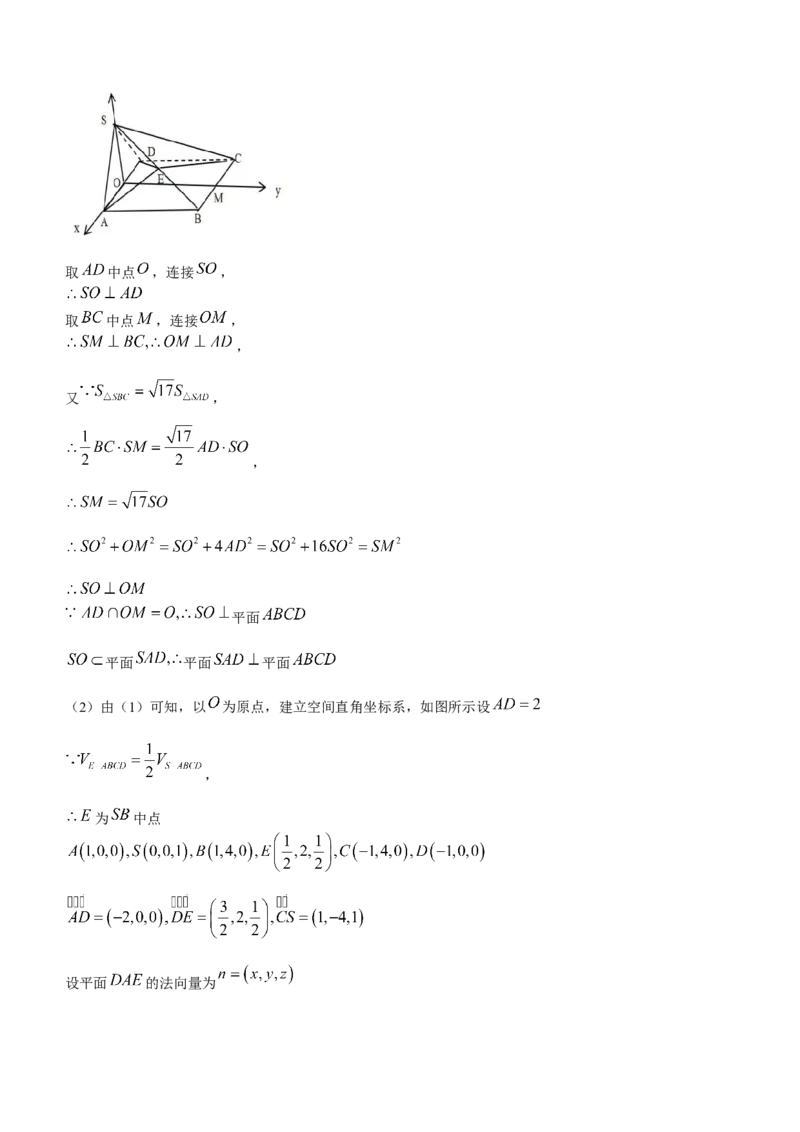
学科网(北京)股份有限公司取 中点 ,连接 ,
取 中点 ,连接 ,
,
又 ,
,
平面
平面 平面 平面
(2)由(1)可知,以 为原点,建立空间直角坐标系,如图所示设
,
为 中点
设平面 的法向量为
学科网(北京)股份有限公司,
令
设直线 与平面 所成夹角为 ,则
直线 与平面 所成夹角的正弦值为
21.【解析】(1)由题意知:
故 ,故
则 ,故双曲线 的标准方程为
(2)假设存在点 满足条件,设其坐标为 ,设 ,
当 斜率存在时,设 方程为
学科网(北京)股份有限公司当 为定值时, ,则
此时
当 斜率不存在时,
存在满足条件的点 ,其坐标为 ,此时 为0
22.解:(1)当 时,
则 ,
所以 的图象在 处的切线方程为: ,
即
(2)方程 有三个不同的根,即 ,
两边同同除以 ,得 ,
令 ,所以 ①
由 ,
当 时, ,当 时, ,
所以函数 在 上递增,在 上递减,
学科网(北京)股份有限公司所以 ,
当 时, ,当 时,
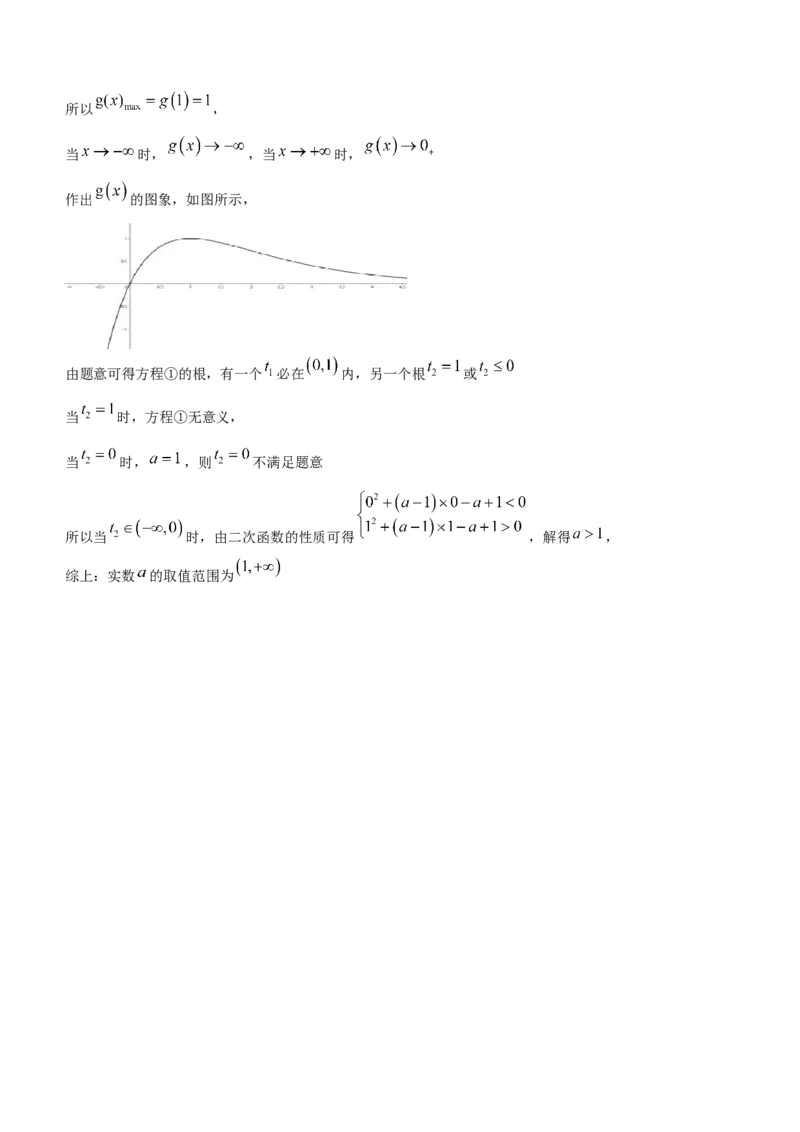
作出 的图象,如图所示,
由题意可得方程①的根,有一个 必在 内,另一个根 或
当 时,方程①无意义,
当 时, ,则 不满足题意
所以当 时,由二次函数的性质可得 ,解得 ,
综上:实数 的取值范围为
学科网(北京)股份有限公司