数学+答案2023-2024苏州高三上期中调研考数学试卷(1)_2023年11月_0211月合集_2024届江苏省苏州市高三上学期期中调研考试_江苏省苏州市2023_2024学年高三上学期期中调研数学

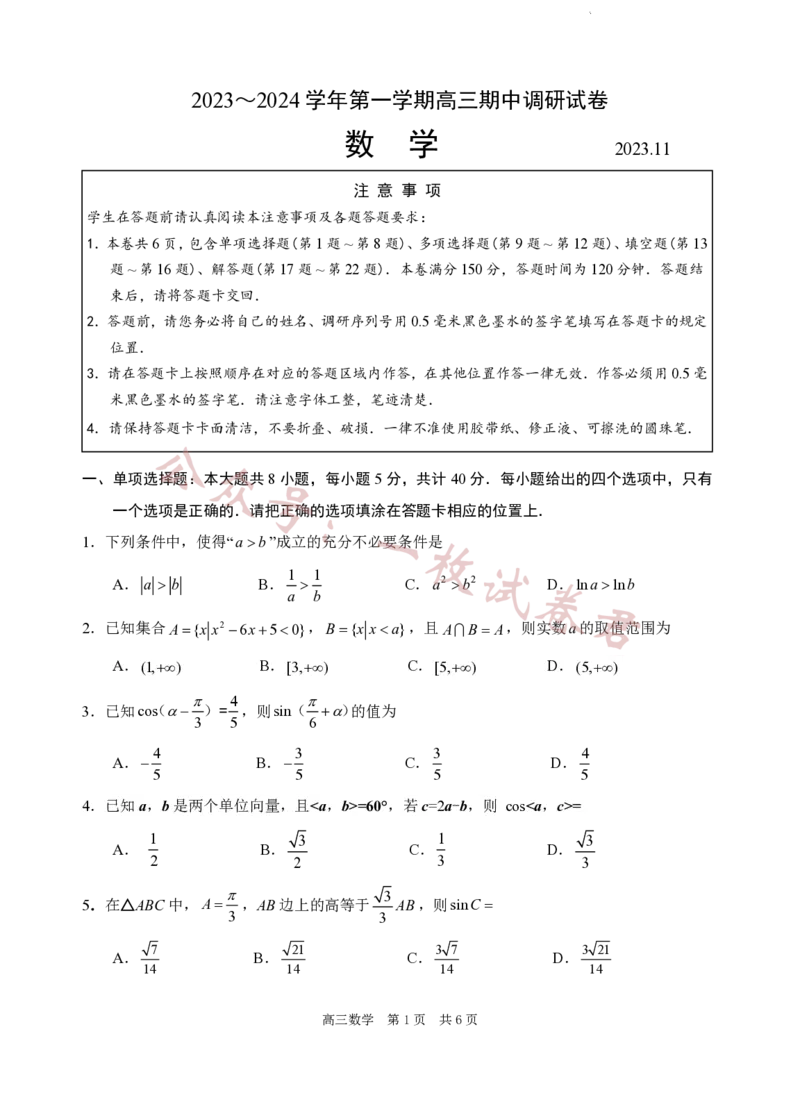
2023～2024 学年第一学期高三期中调研试卷 数 学 2023.11 注 意 事 项 学生在答题前请认真阅读本注意事项及各题答题要求： 1．本卷共6页，包含单项选择题(第1题~第8题)、多项选择题(第9题~第12题)、填空题(第13 题~第16题)、解答题(第17题~第22题)．本卷满分150分，答题时间为120分钟．答题结 束后，请将答题卡交回． 2．答题前，请您务必将自己的姓名、调研序列号用0.5毫米黑色墨水的签字笔填写在答题卡的规定 位置． 3．请在答题卡上按照顺序在对应的答题区域内作答，在其他位置作答一律无效．作答必须用0.5毫 米黑色墨水的签字笔．请注意字体工整，笔迹清楚． 4．请保持答题卡卡面清洁，不要折叠、破损．一律不准使用胶带纸、修正液、可擦洗的圆珠笔． 公 众 一、单项选择题：本大题共号8小题，每小题5分，共计40分．每小题给出的四个选项中，只有 ： 一个选项是正确的．请把正确的选项填涂在答题卡相应的位置上． 一 1．下列条件中，使得“ab”成立的充分不必要条件枚是 试 1 1 A． a  b B．  C．a2 b2 卷 D．lnalnb a b 君 2．已知集合A{x x2 6x50}，B{x xa}，且A B A，则实数a的取值范围为  A．(1,) B．[3,) C．[5,) D．(5,)  4  3．已知co（s  ）= ，则sin（ ）的值为 3 5 6 4 3 3 4 A． B． C． D． 5 5 5 5 4．已知a，b是两个单位向量，且=60°，若c=2a-b，则 cos= 1 3 1 3 A． B． C． D． 2 2 3 3  3 5．在△ABC中，A ，AB边上的高等于 AB，则sinC  3 3 7 21 3 7 3 21 A． B． C． D． 14 14 14 14 高三数学 第1页 共6页 学科网（北京）股份有限公司6．已知曲线yaex xlnx在点(1,ae)处的切线方程为y2xb，则 A．ae1,b1 B．ae1,b1 C．ae,b1 D．ae,b1 7．满足{x m„ x„ n}{y yx2,m„ x„ n}的实数对m，n构成的点(m,n)共有 A．1个 B．2个 C． 3个 D．无数个   1 1 8．已知asin cos ，  ，clog 2log 3，则 13 13 b34 3 2 3 4 A．abc B．acb C．cba D．cab 二、多项选择题：本大题共4小题，每小题5分，共计20分．每小题给出的四个选项中，都有 多个选项是正确的，全部选对的得5分，选对但不全的得2分，选错或不答的得0分．请把 正确的选项填涂在答题卡相应的位置上． 9．已知复数z满足z( 3i)2i，则 A．|z|1 公 B．z的虚部为众3 2 号 ： C．z310 一 D．z2 z 枚  试 10．函数 f(x)tan（2x ），则 4 卷 君  A． f(x)的一个周期为 2 B． f(x)是增函数 3π C． f(x)的图象关于点( ,0)对称 8 π D．将函数ytan2x的图象向右平移 个单位长度可得到 f(x)的图象 4 11．在棱长为2的正方体ABCDABCD 中，E，F 分别为棱AB，AA 的中点，点P在对角线 1 1 1 1 1 AB上，则 1 1 A．三棱锥PCEF体积为 6 2 B．点P到平面CEF的距离为 3 C．APDP的最小值为2 2 2 1 D．四面体BCEF外接球的表面积为14 高三数学 第2页 共6页 学科网（北京）股份有限公司12．对于数列a ，若存在正数M ，使得对一切正整数n，都有 a ≤M ，则称数列a 为有界 n n n 数列；若这样的正数M 不存在，则称数列a 为无界数列．下列说法正确的有 n A．等比数列a 的公比为q，若 q 1，则a 是有界数列 n n n 1 B．若数列a 的通项a  ，则a 是有界数列 n n k2 n k1 a C．若正项数列a 满足：a  n1 (n≥3)，则a 是无界数列 n n 3a n n2 1 1 1 1 D．若数列a 满足：      ，且a （0,1），则a 是有界数列 n a a a aa a 1 n 1 2 n 1 2 n 三、填空题：本大题共4小题，每小题5分，共计20分．请把答案填写在答题卡相应位置上． 13．已知等差数列a 的前n项和为S ，若a 2，5S 6S 30，则a  ▲ ． n n 1 6 5 10 公 14．如图，由3个全等的钝角三角形与中间一个小等边三角形DEF 拼成的一个较大的等边三角 众 号 3 3 形ABC，若AF 3，sinACF  ，则DEF的面积为 ▲ ． ：14 一 枚 试 卷 君 （第14题图） （第15题图） 15．如图，一个半径为3的半圆，C、D两点为直径AB的三等分点，E、F两点为弧AB上的三   等分点，则CFDE= ▲ . 16．已知函数 f(x) 3x2 3，若 m n,且 f(m) f(n)，则m的取值范围为 ▲ ，mn 的取值范围为 ▲ . （本小题第一空2分，第二空3分） 高三数学 第3页 共6页 学科网（北京）股份有限公司四、解答题：本大题共6小题，共计70分．请在答题卡指定区域内作答，解答时应写出文字说 明、证明过程或演算步骤． 17．(本小题满分10分) x x x 已知函数 f(x)2sin cos  3cos . 4 4 2 （1）求 f(x)的最小值及取得最小值时x的取值集合； （2）若 f(x)的图象向右平移m (m0)个单位后得到的函数恰好为偶函数，求m的最小 值． ▲▲▲ 公 众 号 ： 一 枚 试 卷 18． (本小题满分12分) 君 6 7 3 57 在①∠BAC的平分线长为 ；②D为BC中点，AD= ；③AH为BC边上的高，AH= 5 2 19 这三个条件中任选一个，补充在下面的问题中，并解决该问题． △ABC中，角A,B,C的对边为a,b,c，已知b=2，2cosA3acosB. （1）求c; （2）若 ，求∠BAC的大小. 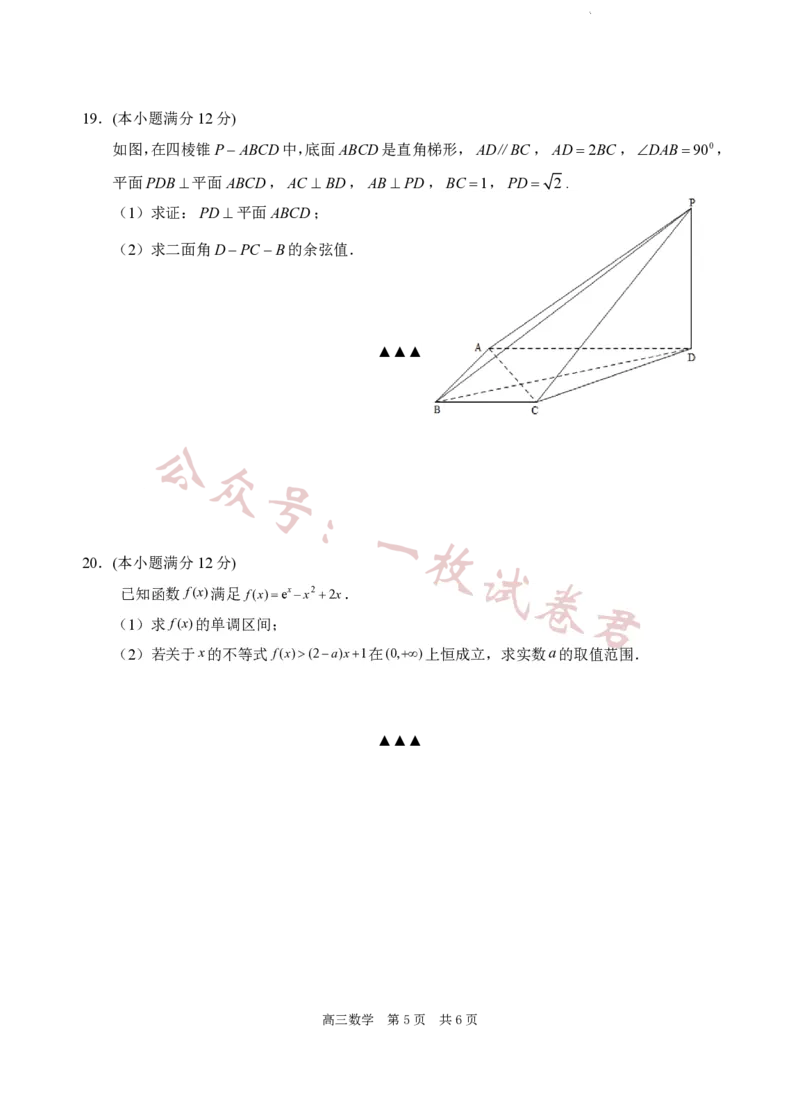注：如果选择多个条件分别解答，按第一个解答计分． ▲▲▲ 高三数学 第4页 共6页 学科网（北京）股份有限公司19．(本小题满分12分) 如图，在四棱锥PABCD中，底面ABCD是直角梯形，AD∥BC，AD2BC，DAB900， 平面PDB平面ABCD，AC BD，ABPD，BC 1，PD 2. （1）求证：PD平面ABCD； （2）求二面角DPCB的余弦值． ▲▲▲ 公 众 号 ： 一 枚 20．(本小题满分12分) 试 卷 已知函数 f(x)满足 f(x)exx22x． 君 （1）求 f(x)的单调区间； （2）若关于x的不等式 f(x)(2a)x1在(0,)上恒成立，求实数a的取值范围． ▲▲▲ 高三数学 第5页 共6页 学科网（北京）股份有限公司21．(本小题满分12分) 已知S 为数列a 的前n项和，a 1，S S 2n22n1． n n 1 n1 n （1）求a 的通项公式； n （2）若b 1,b (1)nb a ，求数列b 的前n项和T ． 1 n1 n n n n ▲▲▲ 公 众 号 ： 22．(本小题满分12分) 一 枚 已知函数 f(x)ax2+(a2)xlnx． 试 （1）若 f(x)在区间(1,2)上有极值，求实数a的取值范围； 卷 君 （2）当0a1时，求证： f(x)有两个零点x ，x (x  x )，且 f(x ) f(x )0． 1 2 1 2 1 2 ▲▲▲ 高三数学 第6页 共6页 学科网（北京）股份有限公司2023～2024 学年第一学期高三期中调研试卷 数学参考答案及评分建议 2023.11 一、单项选择题：本大题共8小题，每小题5分，共计40分． 题 号 1 2 3 4 5 6 7 8 答 案 D C D B D A C B 二、多项选择题：本大题共4小题，每小题5分，共计20分． 题 号 9 10 11 12 答 案 AD AC BCD ABD 三、填空题：本大题共4小题，每小题5分，共计20分． 1 13．20 ; 14． 3; 15． ; 16．( 3, 3) ，(3,3) 2 四、解答题 公 ：本大题共6小题，共计70分． 17．（本小题满分众10分） x 号x x  解：（1）因为 f(x)sin  3cos 2sin(  )，…………………………………………… 2分 2 ：2 2 3 x   5 当   2k,kZ即x4k 一,kZ 时，f(x)取得最小值－2，……………… 4分 2 3 2 3 枚 5 所以f(x)的最小值为－2，此时x的取值集合为{x|x4试k ,kZ}．……………… 5分 3 卷 xm  （2）设 f(x)的图象向右平移m (m0)个单位后得到函数g(x)，则g(x君)2sin(  )， 2 3 x m  x m  因为g(x)为偶函数，所以g(x)g(x)，即sin(   )sin(   )， 2 2 3 2 2 3 x m  m   所以sin cos(  )0恒成立，所以   k,kZ， ……………………… 8分 2 2 3 2 3 2  所以m 2k,kZ ， ………………………………………………………………… 9分 3 5 又因为m0，所以m  ． …………………………………………………………… 10分 min 3 18．(本小题满分12分) 解：（1）由b=2及2cosA3acosB得bcosA3acosB，即bcosAacosB3，……… 2分 b2 c2 a2 a2 c2 b2 由余弦定理得b a 3，…………………………………………… 4 2bc 2ac 分 所以c3． …………………………………………………………………………………… 5分 （2）若选①，记∠BAC=2θ，∠BAC的平分线交BC于D，则有S S S ， △ABC △ABD △ACD ………………………………………………………………………………………… 6分 1 1 1 即 bcsin2 bADsin cADsin，………………………………………………… 7 2 2 2 高三数学期中参考答案 第1页 共6页 学科网（北京）股份有限公司分 12 18 即6sin2 sin sin 即sin2sin，所以2sincossin， ……………… 9分 5 5  1  因为(0, )，所以sin0 从而cos 即 ，………………………………… 11分 2 2 3 2 所以BAC  . …………………………………………………………………………… 12分 3  1   若选②，由于D为BC中点，所以AD (AB AC) ， ………………………………… 6分 2 2 2 2   即4AD  AB  AC 2ABAC， ………………………………………………………… 7分  7     又因为 AD  ， AB 3， AC 2，所以ABAC 3， …………………………… 9分 2   1 即 AB  AC cosBAC 3，所以cosBAC  ， …………………………………… 11分 2 2 又因为BAC(0,)，所以BAC  . ……………………………………………… 12分 3 若选③，由于AH为BC边上的高， 957 144 12 19 在Rt△BAH 中，BH2  AB2 AH2 9  ，所以BH  ，…………… 7分 公 1919 19 19 众 957 49 7 19 在Rt△CAH 中，CH2  AC2 AH2 4  ，所以CH  ， …………… 9分 号 1919 19 19 所以BC BH CH  19， ： AB2  AC2 一BC2 9419 1 由余弦定理得cosBAC    ，………………………… 11分 2ABAC 枚232 2 又因为BAC(0,)，所以BAC  2 . 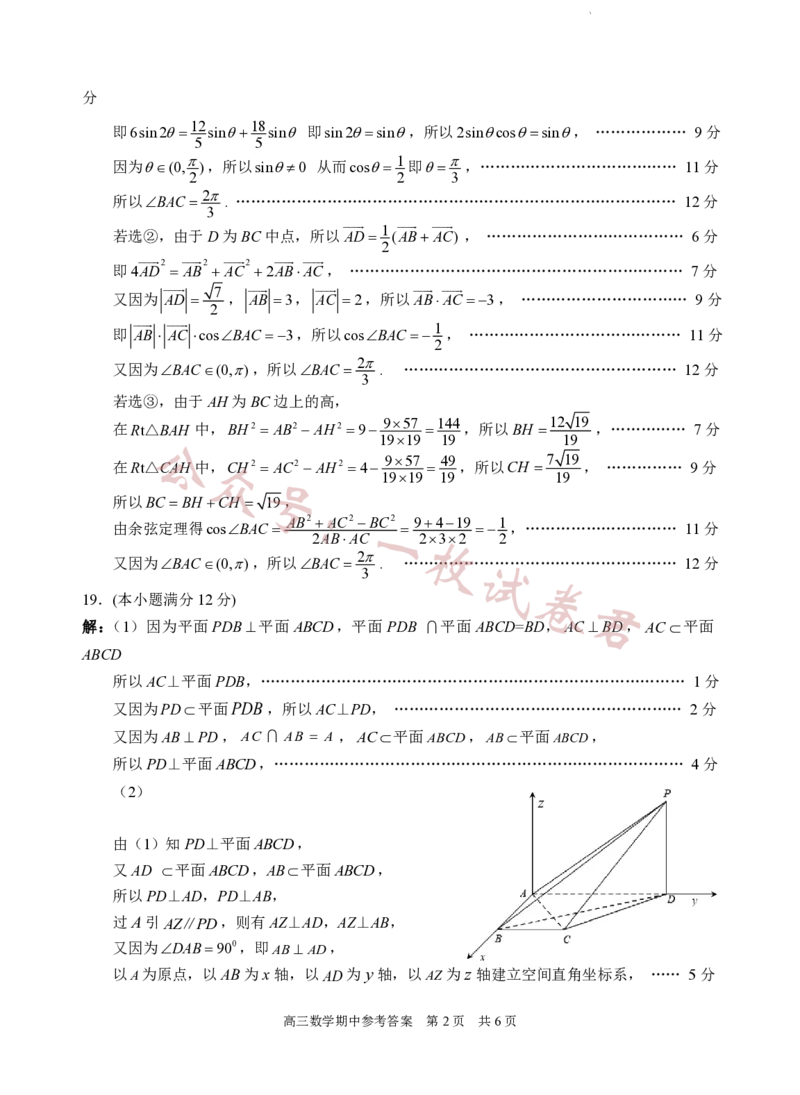……………试………………………………… 12分 3 卷 19．(本小题满分12分) 君 解：（1）因为平面PDB平面 ABCD，平面 PDB 平面 ABCD=BD， AC BD，AC平面  ABCD 所以AC⊥平面PDB，………………………………………………………………………… 1分 又因为PD平面PDB，所以AC⊥PD， ………………………………………………… 2分 又因为ABPD， AC  AB  A ，AC平面ABCD，AB平面ABCD， 所以PD⊥平面ABCD，……………………………………………………………………… 4分 （2） z 由（1）知PD⊥平面ABCD， 又AD 平面ABCD，AB平面ABCD， 所以PD⊥AD，PD⊥AB， 过A引AZ∥PD，则有AZ⊥AD，AZ⊥AB， 又因为DAB900，即AB AD， 以A为原点，以AB为x轴，以AD为y轴，以AZ为z 轴建立空间直角坐标系， …… 5分 高三数学期中参考答案 第2页 共6页 学科网（北京）股份有限公司设ABt(t0)，则A(0,0,0)，B(t,0,0)，C(t,1,0)，D(0,2,0)，P(0,2, 2), 所以AC (t,1,0)，BD(t,2,0)，DP(0,0, 2), 由于ACBD，所以AC BD0， 所以t2 2，即t 2，……………………………………………………………………… 7分 从而C( 2,1,0)，则DC ( 2,1,0)，……………………………………………………… 8分   设平面PDC的一个法向量为n(x,y,z)，则有 nDP0，即  2z0，    nDC0，  2xy0， y 2,  取x1，解得 即n  (1, 2,0) ， ……………………………………………… 9分  z0, 同理，可求得平面PBC 的一个法向量为m(1,0,1)， ………………………………… 10分   1 6 所以|cosm,n|| | ………………………………………………………… 11分 3 2 6 设二面角DPCB的平面角为，为钝角， 所以二 公 面角DPCB的平面角余弦值为  6 . ………………………………………… 12分 6 众 20．(本小题满分12分) 号 ： 解：（1）因为 f(x)exx22x，所以 f(x)ex2x2， ……………………………………… 1分 一 令m(x) f(x)ex2x2，则m(x)ex2， 枚 当x(,ln2)时，m(x)0；当x(ln2,)时，m(x)0试 ． 卷 所以m(x)在(,ln2)上单调递减，在(ln2,)上单调递增． 君 所以m(x) m(ln2)2(2ln2)0， ………………………………………………………… 3分 min 即 f(x)0恒成立， 所以 f(x)的单调递增区间为(,)，无单调递减区间．………………………………… 5分 （2）由题意 f(x)(2a)x1在区间(0,)上恒成立， 1 ex a x 即exx22x2xax1恒成立，即 x x 在区间(0,)上恒成立，……………… 6分 1 ex g(x) x 令 x x ，x(0,)，只需ag(x) max，…………………………………………… 7分 1 exxex (x1)(x1ex) g(x) 1  有 x2 x2 x2 ，x(0,)，…………………………………… 8分 令h(x)x1ex ，x[0,)，有h(x)1ex≤0，从而h(x)≤h(0)0， ………………… 9分 所以当x(0,1)时，g(x)0；当x(1,)时，g(x)0， 所以g(x)在(0,1)上单调递增，在(1,)上单调递减， …………………………………… 10分 所以g(x) max g(1)2e ， ………………………………………………………………… 11分 所以a2e. 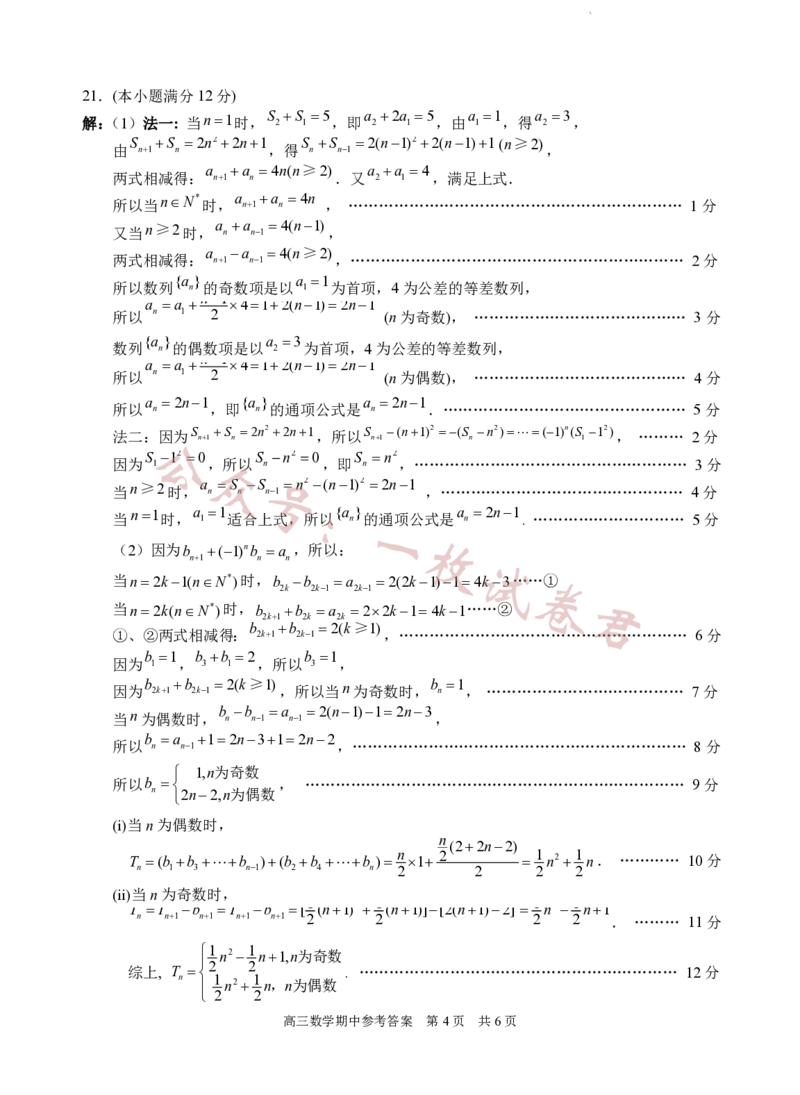………………………………………………………………………………… 12分 高三数学期中参考答案 第3页 共6页 学科网（北京）股份有限公司21．(本小题满分12分) 解：（1）法一: 当n1时， S 2 S 1 5 ，即 a 2 2a 1 5 ，由 a 1 1 ，得 a 2 3 ， S S 2n22n1 S S 2(n1)22(n1)1(n≥2) 由 n1 n ，得 n n1 ， a a 4n(n≥2) a a 4 两式相减得： n1 n ．又 2 1 ，满足上式． 所以当nN* 时， a n1 a n 4n ， ………………………………………………………… 1分 又当n≥2时， a n a n1 4(n1) ， a a 4(n≥2) 两式相减得： n1 n1 ，………………………………………………………… 2分 {a } a 1 所以数列 n 的奇数项是以 1 为首项，4为公差的等差数列， n1 a a  412(n1)2n1 所以 n 1 2 (n为奇数)， …………………………………… 3分 {a } a 3 数列 n 的偶数项是以 2 为首项，4为公差的等差数列， n1 a a  412(n1)2n1 所以 n 1 2 (n为偶数)， …………………………………… 4分 a 2n1 {a } a 2n1 所以 n ，即 n 的通项公式是 n ．………………………………………… 5分 法二： 公 因为S n1 S n 2n22n1，所以S n1 (n1)2 (S n n2)  (1)n(S 1 12)， ……… 2分 因为 S 1 12 0众，所以 S n n2 0 ，即 S n n2 ，……………………………………………… 3分 当n≥2时， a n S n 号S n1 n2(n1)2 2n1 ，………………………………………… 4分 ： 当n1时， a 1 1 适合上式，所以 {a n } 一的通项公式是 a n 2n1 . ………………………… 5分 枚 （2）因为b (1)nb a ，所以： n1 n n 试 当n2k1(nN*)时，b b a 2(2k1)14k3…卷…① 2k 2k1 2k1 君 当n2k(nN*)时，b b a 22k14k1……② 2k1 2k 2k b b 2(k≥1) ①、②两式相减得： 2k1 2k1 ，………………………………………………… 6分 b 1 b b 2 b 1 因为 1 ， 3 1 ，所以 3 ， 因为 b 2k1 b 2k1 2(k≥1) ，所以当n为奇数时， b n 1 ， ………………………………… 7分 当n为偶数时， b n b n1 a n1 2(n1)12n3 ， b a 12n312n2 所以 n n1 ，………………………………………………………… 8分  1,n为奇数 所以b  ， ………………………………………………………………… 9分 n 2n2,n为偶数 (i)当n为偶数时， n (22n2) T (b b  b )(b b  b ) n 1 2  1 n2 1 n． ………… 10分 n 1 3  n1 2 4  n 2 2 2 2 (ii)当n为奇数时， 1 1 1 1 T T b T b [ (n1)2 (n1)][2(n1)2]  n2 n1 n n1 n1 n1 n1 2 2 2 2 ． ……… 11分 1 n2 1 n1,n为奇数 2 2 综上, T  . ……………………………………………………… 12分 n 1 1  n2 n，n为偶数  2 2 高三数学期中参考答案 第4页 共6页 学科网（北京）股份有限公司22．(本小题满分12分) 解：（1）因为 f(x)ax2(a2)xlnx，x(1,2) 1 2ax2(a2)x1 (2x1)(ax1) 所以 f(x)2axa2   ， ………………………… 1分 x x x ①当a≤0时， f(x)0 f(x) (1,2) f(x) (1,2) 所以 在 上单调递减，所以 在 上无极值点，………………………… 2分 1 1 x(0, ) x( ,) ②当a0时，当 a 时， f(x)0 ；当 a 时， g(x)0 ， 1 1 (0, ) ( ,) 所以 f(x) 在 a 上单调递减，在 a 上单调递增． 1 所以 f(x) 的极小值点为a，无极大值点， 1 (1,2) 因为 f(x) 在 (1,2) 上有极值，所以a ， 1 a1 所以 2 . …………………………………………………………………………… 4分 (2x1)(ax1) f(x) （2）当0a1时， x ，x0 公 1 1 1 1 f(x)  f( )ln  1 1 由(1)知： 众 极小 a a a ，0a1，a 1 t 号 令 a ，t1，则 f(t)lntt1 ： 1 f(t) 10 因为 t ， t(1,) 恒成立 一 ，所以 f(t) 在 (1,) 上单调递减 1 枚 f(x)  f( )0 所以 f(t) f(1)0 即 极小 a ， ……………试…………………………………… 5分 1 a a2 1 a a 2 卷 f( )  ln   1 0 因为 e e2 e e e2 e e ， 君 1 1 1 (0, ) f( ) f( )0 由(1)知： f(x) 在 a 上单调递减，且 e a ， 1 (0, ) 所以 f(x) 在 a 上存在唯一的零点 x 1，使 f(x 1 )0 ，…………………………………… 6分 3 9 3(a2) 3 3 3 f( )  ln 3 ln 因为 a a a a a a， 3 3 3 ln  1,0a1 f( )3140 又 a a ，所以 a ， 1 1 3 ( ,) f( ) f( )0 由(1)知 f(x) 在 a 上单调递增，且 a a ， 1 ( ,) 所以 f(x) 在 a 上存在唯一的零点 x 2，使 f(x 2 )0 ． f(x) x x (x x ) 所以 有两个零点 1， 2 1 2 . ……………………………………………………… 7分 f(x ) f(x )0 下面证明 1 2 ： 0x x 设 1 2，则  f(x)ax2(a2)x lnx a(x2x)2x lnx 0  1 1 1 1 1 1 1 1 ． f(x )ax 2(a2)x lnx a(x 2x )2x lnx 0 2 2 2 2 2 2 2 2 a[(x2 x 2)(x x )]2(x x )(lnx lnx )0 两式相减： 1 2 1 2 1 2 1 2 高三数学期中参考答案 第5页 共6页 学科网（北京）股份有限公司x a(x x )(x x 1)2(x x )ln 1 0 1 2 1 2 1 2 x 即 2 x 2(x x )ln 1 1 2 x 所以a 2 ， ……………………………………………………………… 8分 (x x )(x x 1) 12ax22(a12)2x1 1 f(x) 2ax a2 因为 x x 1 1 1 1 f(x ) f(x )2a(x x )(  )2(a2)2a(x x 1)(  )4 1 2 1 2 x x 1 2 x x 所以 1 2 1 2 x x 2(x x )ln 1 2ln 1 1 2 x 1 1 x 1 1 2(x x 1) 2 (  )4 2 (  )，…………… 9分 1 2 (x x )(x x 1) x x (x x ) x x 1 2 1 2 1 2 1 2 1 2 x 2ln 1 要证： f(x ) f(x )0，即证： x 2 ( 1  1 )0(0x x )， 2l 1 n x 1 ( 1 2  1 )(x x ) (x 01 x 2 ) x 12ln x 2 x 1  x 1  x 2 1 0 2 x x x 1 2 x x x 只要证： 2 1 2 ，即证： 2 2 1 . …………………… 10分 x t 1 ,t(0,1) 2lntt 1 0 令 x 2 ，即证： t ， t(0,1) ． m( 公 t)2lntt 1 m(t) 2 1 1  (t1)2 0 令 众t ， t(0,1) ，则 t t2 t2 ， t(0,1) 恒成立 号 所以 m(t) 在 (0,1) 上单调递减，：所以 m(t)m(1)0 ． x x x 2ln 1  1  2 0 一 x x x 即 2 2 1 成立， 枚 f(x) x x (x  x ) f(x ) f(x )试0 故 有两个零点 1， 2 1 2 ，且 1 2 . …………………………… 12分 卷 君 高三数学期中参考答案 第6页 共6页 学科网（北京）股份有限公司