文档内容
2024~2025 学年第一学期高二年级期末学业诊断
数学试卷
(考试时间:上午 8:00—10:00)
说明:本试卷为闭卷笔答,答题时间 120 分钟,满分 150 分.
一、单项选择题(本题共 8 小题,每小题 5 分,共 40 分.在每小题给出的四个选项中,只有
一项是符合题目要求的)
1. 抛物线 y2=4x 的焦点坐标是
A. (0,2) B. (0,1) C. (2,0) D. (1,0)
2. 双曲线 的顶点坐标为( )
A. , B. , C. , D. ,
3. 已知抛物线以圆 的圆心为焦点,则其标准方程为( )
A. B. C. D.
4. 已知双曲线的一个焦点为 ,其离心率 ,则该双曲线的渐近线方程为( )
A. B. C. D.
5. 已知双曲线 C 以椭圆方程 E: 的焦点为顶点,以 E 的顶点为焦点,则双曲线 C 的标准方程为
( )
A. B. C. D.
6. 已知点 P 是抛物线 上一点,则点 P 到直线 的距离的最小值为( )
A. B. 2 C. D.
7. 已知直线 与双曲线 相交于 、 两个不同点,点 是
的中点,则双曲线 的离心率为( )
第 1页/共 4页
学科网(北京)股份有限公司A. B. C. D.
8. 古希腊数学家帕普斯在他的著作《数学汇编》中对圆锥曲线给出了统一定义,即到定点的距离与到定直
线的距离的比是常数 e 的点的轨迹叫做圆锥曲线.当 时,轨迹为椭圆;当 时,轨迹为抛物线;
当 时,轨迹为双曲线.若方程 表示的曲线是双曲线,则实数 k 的取值范
围为( )
A. B. C. D.
二、多项选择题(本题共 3 小题,每小题 6 分,共 18 分.在每小题给出的四个选项中,有多
项符合题目要求.全部选对的得 6 分,部分选对的得部分分,有选错的得 0 分)
9. 已知 , ,双曲线 : 与 : ,则下列结论正确的是( )
A. 它们的实轴长相等 B. 它们的焦点相同
C. 它们的离心率相等 D. 它们的渐近线相同
10. 已知直线 l: ,抛物线 C: ,则下列结论正确的是( )
A. 直线 l 过定点
B. 当 时,直线 l 与抛物线 C 相切
C. 当 时,直线 l 与抛物线 C 有两个公共点
D. 当直线 l 与抛物线 C 无公共点时, 或
11. 平面内到两定点距离之积为常数的点的轨迹称为卡西尼卵形线,它是 1675 年法国天文学家卡西尼在研
究土星及其卫星的运行规律时发现的.已知平面直角坐标系中, , ,动点 P 满足
,记动点 P 的轨迹为曲线 C,则下列结论正确的是( )
A. 曲线 C 关于原点对称 B. 点 P 的横坐标的取值范围为
C. 面积的最大值为 2 D. 的取值范围为
三、填空题(本题共 3 小题,每小题 5 分,共 15 分)
12. 抛物线 准线方程是___________________.
第 2页/共 4页
学科网(北京)股份有限公司13. 已知过抛物线 C: ( )的焦点 F 且斜率为 的直线与 C 相交于 A,B 两个不同点,若
,则 (O 是坐标原点)的面积为__________.
14. 已知双曲线 E: 的左焦点为 F,点 M 是 E 右支上的动点,点 N 是圆 上的
动点,则 的最大值为__________.
四、解答题(本题共 5 小题,共 77 分.解答应写出文字说明、证明过程或演算步骤)
15. (1)已知抛物线 C 经过点 ,求 C 的标准方程和焦点坐标;
(2)已知双曲线 C 经过点 , ,求 C 的标准方程和焦点坐标.
16. 已知点 在抛物线 C: ( )上,且点 P 到 C 准线的距离为 2.
(1)求 C 方程;
(2)设圆 与抛物线 C 相交于 A,B 两个不同点,求 的值.
17. 已知点 , ,动点 P 满足 ,记点 P 轨迹为曲线 C.
(1)求曲线 C 的方程,并说明曲线 C 的形状;
(2)若双曲线 E 右焦点是曲线 C 的对称中心,其渐近线是曲线 C 的切线,求双曲线 E 的标准方程.
18. 已知点 , ,直线 PM 与 PN 相交于点 P,且它们的斜率之积为 ,记点 P 的轨迹
为曲线 C.
(1)求曲线 C 的标准方程;
(2)若直线 l: 交曲线 C 于 A,B 两点,点 (不在直线 l 上),是否存在实数 k,使得直
线 QA 与 QB 的斜率之和为 0?若存在,求出 k 的值;若不存在,说明理由.
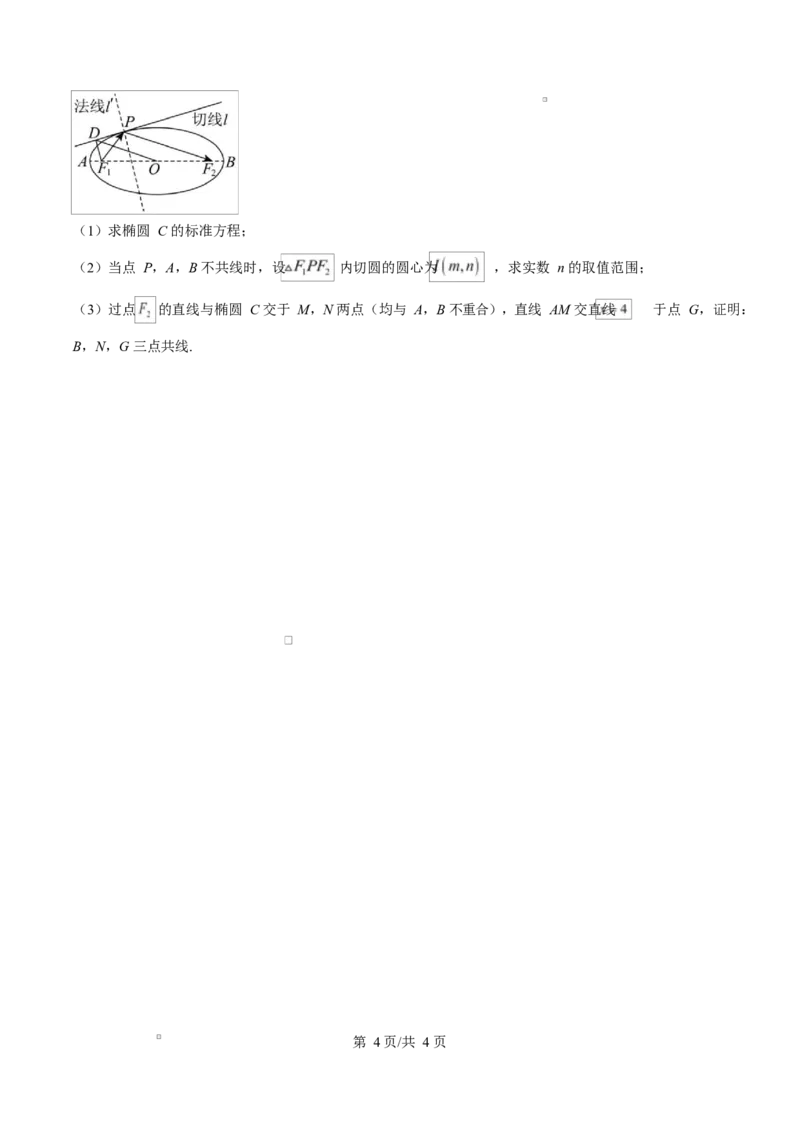
19. 椭圆有很好的光学性质.如图,从椭圆 C 的一个焦点 发出的光线,被椭圆上点 P 反射后,反射光线经
过另一个焦点 ,且椭圆在点 P 处的切线 l 与 的平分线 l'(即法线)垂直.已知椭圆 C 的中心为坐
标原点 O,左、右顶点分别为 A,B,焦点为 , .由 发出的光线经椭圆 C 两次反射
后回到 所经过的路程为 8c.过点 作直线 l 的垂线,垂足为 D, .
第 3页/共 4页
学科网(北京)股份有限公司(1)求椭圆 C 的标准方程;
(2)当点 P,A,B 不共线时,设 内切圆的圆心为 ,求实数 n 的取值范围;
(3)过点 的直线与椭圆 C 交于 M,N 两点(均与 A,B 不重合),直线 AM 交直线 于点 G,证明:
B,N,G 三点共线.
第 4页/共 4页