文档内容
泸州市高2022级第一次教学质量诊断性考试
数学参考答案
一.选择题
题号 1 2 3 4 5 6 7 8 9 10 11
答案 D C B C A B A D CD ACD BD
二.填空题
12. 13. 14.
π
15.解(1) 2sin(2x+ )>❑√3
3
π ❑√3
sin(2x+ )> .
3 2
π π 2
2kπ+ <2x+ <2kπ+ π
3 3 3
1
2kπ<2x<2kπ+ π
3
π
kπ0时,
π
(2)g(x)=2sin(x+ )−❑√3,
3
π 2
g( )=2sin π−❑√3=0.
3 3
x 2
∴k=g′ ( )=2cos π=−1.
3 3
π π
∴y=g(x)在( ,g( ))处而切线方程为:.
3 3
π
y=−(x− ) .
3
π
x+ y− =0.
3
16.解(1) n=1时、2S =3a −9
1 1
.
∴a =S =9
1 1
n≥2时
第 1 页 共 5 页
学科网(北京)股份有限公司.
2(S −S )=3a −3a
n n−1 n n−1
.
∴2a =3a −3a
n n n−1
故: a
n =3
a
n−1
an是以9为首项,公比为3的等比数列
.
a =9×3n−1=3n+1
n
b .
(2)∵ n+1=a ,b =3
b n 1
n
b b b .
∴b = n ⋅ n−1 ⋯ 2 ⋅b
n b b b 1
n−1 n−2 1
.
=a ⋅a ⋯a ⋅b
n−1 n−2 1 1
.
=3n ⋅3n−1 ⋅3n−2 ⋯32 ⋅3
.
=31+2+3+⋯+n
n(n+1).
=3 2
n(n+1) n(n+1)
log b =log = .
3 n 3 2 2
1 2
: = .
log b n(n+1)
3 m
2 2 2
= + +⋯+ .
1×2 2×3 100×101
1 1 1 1 1
=2(1− + − +⋯+ − ) .
2 2 3 100 101
1
=2(1− ) .
101
.
=
cosA cosB+cosC
17.解(1)由正法是理得: =
sin A sinB+sinC
∴sinAcosB+sinAcosC=cosAsinB+cosAsinC ∴sinAcosB-
第 2 页 共 5 页
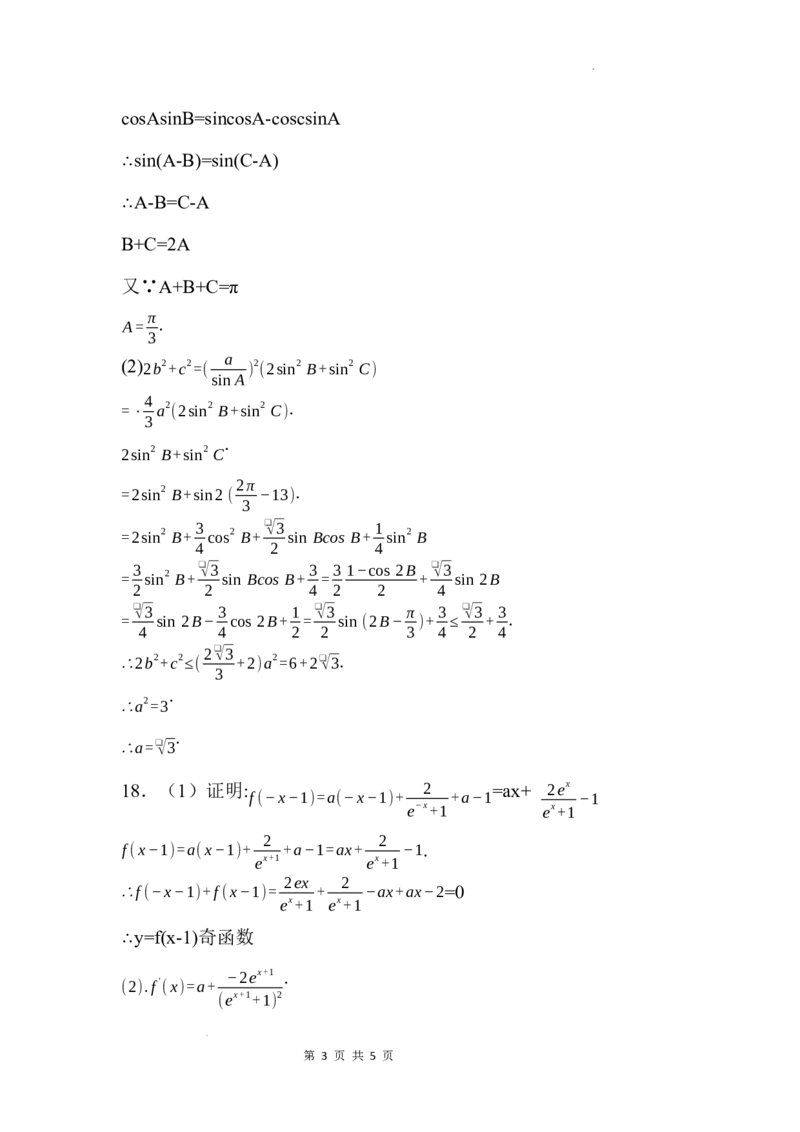
学科网(北京)股份有限公司cosAsinB=sincosA-coscsinA
∴sin(A-B)=sin(C-A)
∴A-B=C-A
B+C=2A
又∵A+B+C=π
π
A= .
3
a
(2)2b2+c2=(
)
2 (2sin2B+sin2C)
sin A
4
=⋅ a2 (2sin2B+sin2C) .
3
.
2sin2B+sin2C
2π
=2sin2B+sin2( −13) .
3
3 ❑√3 1
=2sin2B+ cos2B+ sinBcosB+ sin2B
4 2 4
3 ❑√3 3 3 1−cos2B ❑√3
= sin2B+ sinBcosB+ = + sin2B
2 2 4 2 2 4
❑√3 3 1 ❑√3 π 3 ❑√3 3
= sin2B− cos2B+ = sin(2B− )+ ≤ + .
4 4 2 2 3 4 2 4
2❑√3
∴2b2+c2≤( +2)a2=6+2❑√3.
3
.
∴a2=3
.
∴a=❑√3
18.(1)证明: 2 =ax+ 2ex
f(−x−1)=a(−x−1)+ +a−1 −1
e−x+1 ex+1
2 2
f(x−1)=a(x−1)+ +a−1=ax+ −1.
ex+1 ex+1
2ex 2
∴f(−x−1)+f(x−1)= + −ax+ax−2=0
ex+1 ex+1
∴y=f(x-1)奇函数
−2ex+1 .
(2).f′ (x)=a+
(ex+1+1) 2
第 3 页 共 5 页
学科网(北京)股份有限公司−2
=a+
1 .
ex+1+ +2
ex+1
−2 1
a+ =a−
√ 1 2
2❑ex+1 +2
ex+1
2
(3)f(x)=a(x+1)+ −1 显然f(-1)=0
ex+1+1
由(1)可得f(x)周象关于(-1,0)对称
三个零点,等价于f(x)在(-1, )有1个零点
令
2
g(t)=at+ −1=0在(0,+ )中的∵有1个零点
et+1
1 −2
∴a= + = ℎ(t),
t t(et+1)
在 单减
1
∴a1
n+1 n
n(n−1) d d
S =n+ d = n2+(1− )n
n 2 2 2
d 1
n2+(1− )n≤n2+ n.
2 2
2n−1 2(n−1)+1 1
d≤ = =2+ .( )
n−1 n−1 n−1
∴d≤2综上得: 11, (a −a )≤1.
n+1 n 3 n+1 n
.
∴1