文档内容
年下学期 月高二联考数学
2025 10
参考答案、提示及评分细则
.答案
1【 】B
解析 设z ( 2-i ) 2 (2-i) 2 3-4i 所以z在复平面内对应的点的坐标为 位于第二
【 】 = = = =-3+4i, (-3,4),
i -1 -1
象限 故选 .
, B
.答案
2【 】C
解析 点M 关于平面yOz的对称点为 故选 .
【 】 (1,-2,3) (-1,-2,3), C
.答案
3【 】D
2 2 2
解析 易得这三个数据的平均数x 12+15+18 方差s2 (12-15)+(15-15)+(18-15) 故
【 】 = =15, = =6,
3 3
选 .
D
.答案
4【 】C
解析 当 θ 时 直线l的方程为x 此时直线l的倾斜角α π 当 θ 时 直线l的斜率为
【 】 cos=0 , =-2, = ; cos ≠0 ,
2
α 1 因为 θ 所以 1 即 α
tan = θ, cos∈[-1,0)∪(0,1], θ∈(-∞,-1]∪[1,+∞), tan ∈(-∞,-1]∪
cos cos
é ö æ ù
又因为α 所以结合正切函数的图象可得α ê êπ π÷ çπ 3π ú ú 综上可得 直线l的倾
[1,+∞), ∈[0,π), :∈ ë , ø∪è , û, :
4 2 2 4
é ù
斜角α的取值范围是ê êπ 3π ú ú 故选 .
ë , û, C
4 4
.答案
5【 】AB
解析 当m n 时e 与e 共线 则e e e 共面 符合题意 当m n 时e e
【 】 =4,=1 ,2 3 , 1,2,3 ,A ; =3,=2 ,1=(1,1,0),2=
e 故e e 1e 则e e e 共面 符合题意 故选 .
(2,3,1),3=(2,4,2), 2= 1+ 3, 1,2,3 ,B , AB
2
.答案
6【 】D
( ) (α )
解析 由余弦二倍角公式可得 α π 2 π 5
【 】 cos - =2cos - -1=- ,
6 2 12 8
( ) ( )
所以 α π 2α π 39 故选 .
sin - =± 1-cos - =± , D
6 6 8
高二数学试题参考答案 第 页 共 页
【 1 ( 7 )】.答案
7【 】C
解析 由题意设圆台OO 的上 下底面圆的半径分别为r r 则其母线长为 r 高为 r 可得球O的半径
【 】 1 2 、 ,2 , 2 , 3 ,
为 r 故4π r3 32 解得r 所以该圆台的表面积S r2 r2 r r r r2
2 , (2 )= π, =1, =π +4π +π(+2 )2 =11π =11π,
3 3
故选 .
C
.答案
8【 】B
x y
解析 设OD→ OA→ OE→ OB→ 因为 z 所以OP→ xOA→ yOB→ zOC→
【 】 =4 =(4,0,0), =2 =(0,2,0), + + =1, = + + =
4 2
x y
OD→ OE→ zOC→ 所以DECP四点共面 当OP 平面DEC时 OP→ 有最小值.CD→
+ + , , , , , ⊥ ,| | =(4,0,-1),
4 2
ì
ïm CD→ a c
ï =4 - =0
CE→ 设平面DEC的一个法向量m abc 则í 取a 则b c
=(0,2,-1), =(,,), ïï , =1, =2,=4,
îm CE→ b c
=2 - =0
m OC→
所以m 为平面DEC的一个法向量 所以O到平面DEC的距离d | | 4 21 故选 .
=(1,2,4) , = m = , B
| | 21
.答案
9【 】BD
解析 当a b 时a2 b 则a2 b 不成立 故 错误
【 】 = =1 - =0, - >0 , A ;
a b 2 a b ab ab a b 当且仅当a b 时取等号 故 a b 故
( + )= + +2 =2+2 ≤2+ + =4, = =1 , + ≤2, B
正确
;
( ) ( ) b a b a b a
1 1 a b 1 1 当且仅当 即a b 时等号成立
2a+b =(+ )a+b =2+a+b≥2+2 ab=4, a=b, = =1 ,
则1 1 故 错误
a+b≥2, C ;
a b ab 因为 a b ab 当且仅当a b 时等号成立 所以ab 于是 ab
log2 +log2 =log2 , 2= + ≥2 , = =1 , ≤1, log2 ≤
即 a b 故 正确 故选 .
log21=0,log2 +log2 ≤0, D , BD
.答案
10【 】ACD
解析 因为平行六面体ABCD ABCD 的各面均为含2π内角的菱形 所以a b c 且ab
【 】 - 1 1 1 1 , ||=||=||=1, ,,
3
c两两之间的夹角均为π 所以a b a c b c 1 故a c b c a b a c c b c c
, = = = , (+ )(+ )= + + + =
3 2
1 1 1 5 故 正确 AC→ BD→ a b c a b c a a b b c c b c
+ + +1= , A ; 1 1=(+ + )(- + + )=- + + +2 =
2 2 2 2
故 错误 AC→ 2 a b c 2 a 2 b 2 c 2 a b 故 AC→ 故 正确
2, B ;| 1| =| + + | =| | +| | +| | +6 =6, | 1|= 6, C ;
高二数学试题参考答案 第 页 共 页
【 2 ( 7 )】AB→ AD→ a c b c
BAD 1 1 (+ )(+ ) 5 1 又 ab 1 故 BAD ab 故 正
cos∠ 1 1= AB→ AD→ =a c b c = > , cos‹,›= , ∠ 1 1<‹,›, D
| 1|| 1| | + |×| + | 6 2 2
确 故选 .
, ACD
.答案
11【 】ACD
解析 不妨取空间内一点C使得n BC→ 则n AC→ 由α β 可知BC→ AC→ 故由投影向量性质可知
【 】 1= , 2= , ⊥ ⊥ ,
AB→ AC→ AC→ 2 故 正确 同理 AB→ n AB→ BC→ BC→ 2 n 2 故 错误 由α β 可得
| |=| |, A ; | 1|=| |=| |=| 1|, B ; ∥
n n 故可设n λn 故AB→ n n λ n 可知n与AB→共线 故 正确 由l β 可得AB→ n 显
1∥ 2, 2= 1, = 2- 1=(-1)1, 1 , C ; ∥ 2=0,
然AB→与n不共线 于是n n AB→不与n共线 故两平面不平行 故二者只能相交 故 正确 故选 .
2 , 1= 2- 2 , , , D , ACD
.答案
12【 】1
m
解析 由l 与l 的斜率相等 可得 +3 解得m 故答案为 .
【 】 1 2 , m =2, =1, 1
+1
.答案
13【 】(0,1]
{ x }
【 解析 】 由题意知A = x | 2 x - ≥0 ={ x |0< x ≤2}, B ={ y | y >1}, 故 ∁ R B ={ y | y ≤1}, 所以A ∩(∁ R B )=
故答案为 .
(0,1], (0,1]
.答案
14【 】5
解析 由l ml n得AB→ AD→ AB→ BC→ 由AB→ BC→ 得AB→ AC→
【 】 ⊥ ,⊥ =0, =0, =0 =
AB→2 由AB→ CD→ 可得AB→ AC→ AB→ AD→ 由AD→ BC→ 可得AC→
, =-4 = +4=4, =2
AD→ AB→ AD→ 而AB→ AC→ AB→2 得AB .由 BAC DAC得
= +2=2, =4= , =2 ∠ =∠
AB→ AC→ AC→ AD→
BAC DAC 即 | | | | 即4 2 解得AD 故由勾股定理得BD
cos∠ =cos∠ , AB→ AC→= AC→ AD→ , =AD, =1, =
| || | | || | 2
AB2 AD2 故答案为 .
+ = 5, 5
.解析 由直线l x y y 2x 8可得斜率为 2 分
15【 】(1) 2:2 +3 -8=0⇒ =- + - , 1
3 3 3
所以根据垂直关系可设所求直线方程为y 3x b 分
= + , 3
2
则依题意有 3 b 解得b 5 分
4= ×1+ , = , 6
2 2
所以所求直线的斜截式方程为y 3x 5. 分
= + 7
2 2
{x y
-2 +3=0 x y
联立 解得交点坐标为 设直线方程为 ab 分
(2) (1,2), a+b=1(,≠0), 9
x y
2 +3 -8=0
高二数学试题参考答案 第 页 共 页
【 3 ( 7 )】ì ï a b
=-
ï
依题意í 解得a b 分
ï , =-1,=1, 12
ï1 2
îa+b=1
所以所求直线的一般式方程为x y . 分
- +1=0 13
.解析 设AC BD O 连接OE 过D向OE作垂线 垂足为H 分
16【 】(1) ∩ = , , , , 1
因为平面BDE 平面EAC 平面BDE 平面EAC OE DH OE DH 平面
⊥ , ∩ = , ⊥ , ⊂
BDE 所以DH 平面EAC 分
, ⊥ , 3
因为AC 平面EAC 所以DH AC
⊂ , ⊥ ,
因为DE 平面ABCDAC 平面ABCD 所以DE AC 分
⊥ , ⊂ , ⊥ , 5
因为DH DE DDH DE 平面BDE 所以AC 平面BDE
∩ = , , ⊂ , ⊥ ,
因为BDC 平面BDE 所以AC BD. 分
⊂ , ⊥ 6
因为AD CD 结合 可知底面为正方形 以D为原点 DADCDE所在直线分别为xyz轴 建立
(2) ⊥ , (1) , , , , ,, ,
空间直角坐标系 则A C E B F 分
, (2,0,0), (0,2,0), (0,0,2), (2,2,0), (2,0,1), 8
AC→ AE→ BF→ FE→
=(-2,2,0), =(-2,0,2), =(0,-2,1), =(-2,0,1),
ì
ïn AC→ x y
ï =-2 +2 =0
设平面EAC的一个法向量为n xyz 则í 令x 得n . 分
=(,,), ïï , =1 ,=(1,1,1) 10
în AE→ x z
=-2 +2 =0
ì
ïm BF→ y z
ï =-2 0+ 0=0
设平面BEF的一个法向量为m x y z 则í 令z
=(0,0,0), ï
ï
, 0=2
îm FE→ x z
=-2 0+ 0=0
得 m . 分
, =(1,1,2) 12
n m
设平面BEF与平面EAC的夹角为θ 则 θ | | 4 22 分
, cos=n m = = , 14
||| | 3× 6 3
即平面BEF与平面EAC的夹角的余弦值为22. 分
15
3
.解析 由正弦定理可得 B A C A A C 分
17【 】(1) 2sin cos +sin cos +sin cos =0, 2
所以 B A A C B A B 分
2sin cos +sin( + )=2sin cos +sin =0, 4
因为 B 所以 A 1.因为A 所以A 2 . 分
sin ≠0, cos =- ∈(0,π), = π 6
2 3
由题意可得BC B C π. 分
(2) =6, = = 7
6
高二数学试题参考答案 第 页 共 页
【 4 ( 7 )】设 ADE α 则 AED 2π α. 分
∠ = , ∠ = - 8
3
AB AD
在 ABD中 由正弦定理得 所以AD 3 分
△ , α = , = α; 10
sin(π- ) π sin
sin
6
DE AD
在 ADE中 由正弦定理 得 所以DE 3 1 3
△ , ,
π
= (
2π α
), =
2
×
α
(
2π α
)=
sin
2α
+ 3sin
α
cos
α=
sin sin - sinsin -
3 3 3
3 3 . 分
α = ( ) 13
1-cos2 3 α 1 α π
+ sin2 +sin2 -
2 2 2 6
由π α π 得π α π 5π 所以当 α π π 即α π时 DE取得最小值为 . 分
< < , <2 - < , 2 - = , = , 2 15
6 2 6 6 6 6 2 3
.解析 如图 以点D为坐标原点 分别以DA→ DC→ DH→为xyz轴 建立空间直角坐标系 则A
18【 】 , , , , ,, , , (2,0,0),
D C B E F G H . 分
(0,0,0), (0,2,0), (2,2,0), (2,0,2), (2,2,2), (0,2,2), (0,0,2) 2
因为M N分别为棱FG和GH 的中点 所以M N . 分
, , (1,2,2), (0,1,2) 3
设点G到平面α的距离为d 等价于到平面AMN 的距离为d.三棱锥G AMN
(1) , -
的体积V 1S d 其中S 表示 AMN 的面积 三棱锥G AMN 的体积
= △ AMN , △ AMN △ , -
3
等于三棱锥A GMN的体积 分
- , 4
则有1 S d 1 S AE MN 且 AM AN 分
△ AMN = △ GMN| |,| |= 2, | |=| |=3, 6
3 3
( )
则S △ AMN = 1 | MN | | AM | 2 - 1 | MN | 2 = 17.
2 2 2
又S 1 GM GN 1 AE . 分
△ GMN = | || |= ,| |=2 8
2 2
所以d 2 17 即点G到平面α的距离为2 17. 分
= , 9
17 17
(2)
点P在棱DH 上
,
设P
(0,0,
z
P)
.由P在平面AMN上
,
则AP→与AM→
,
AN→共面
,
即存在实数s
,
t使得AP→
sAM→ tAN→ 分
= + , 10
{ s t
- -2=-2
所以 z s t 可得 解得s 2t 4 则z 4
(-2,0,P)= (-1,2,2)+ (-2,1,2), , =- ,= , P = ,
s t 3 3 3
2+ =0
( )
故P 4 DP 4. 分
0,0, ,| |= 11
3 3
高二数学试题参考答案 第 页 共 页
【 5 ( 7 )】{ u v
- -2 =0
同理
,
设Q
(2,2,
z
Q),
令AQ→
=
uAM→
+
vAN→
,
则
,
解得u
=
4
,
v
=-
2
,
u v 3 3
2 + =2
( )
则z
Q =
4
,
Q
2,2,
4
,
则PQ→
=(2,2,0), 12
分
3 3
平面ABCD的一个法向量为k 且PQ→ k 则PQ→ k.
=(0,0,1), =0, ⊥
又直线PQ不在平面ABCD内 所以PQ 平面ABCD. 分
, ∥ 13
( )
由题 PF→ 2 EB→ EC→ .设平面EBC的法向量为n xyz 则
(3) , = 2,2, , =(0,2,-2), =(-2,2,-2) =( ,,),
3
ì
ïn EB→ y z
ï =2 -2 =0
í 解得y zx 令y 得法向量n . 分
ïï , = ,=0, =1, =(0,1,1) 15
în EC→ x y z
=-2 +2 -2 =0
2
PF→ n |20+21+ 1|
设直线PF与平面EBC所成角为 φ.则 φ | | 3 2 38 即直线PF与平
sin = PF→ n = = ,
| ||| 76 19
2
9
面EBC所成角的正弦值为2 38. 分
17
19
.解析 显然EB2 EA2 AB2 于是有EB2 BC2 EC2 故BE BC 分
19【 】(1) = + =5, + = , ⊥ , 1
由BC AB AB BE B AB 平面PABBE 平面PAB可知BC 平面
⊥ , ∩ = , ⊂ , ⊂ ⊥
PAB 分
, 3
由PA 平面PAB可知PA BC 分
⊂ ⊥ , 4
由PA ABAB AC AAB 平面ABCDAC 平面ABCD可得PA 平面
⊥ , ∩ = , ⊂ , ⊂ ⊥
ABCD. 分
5
方法一 建系法 以A为坐标原点 BC→的方向为x轴正方向 AB→的方向为y轴正方向 AP→的方向为
(2)(i) : : , , ,
z轴正方向 建立空间直角坐标系Axyz 分
, , 6
则A B C P E . 分
(0,0,0), (0,2,0), (2,2,0), (0,0,2), (0,0,1) 7
设Ox y z 则由 OE OA OB OC 即x2 y2 z2 x2
(0,0,0), | |=| |=| |=| |, 0+ 0+ 0= 0+
y 2 z2 x 2 y 2 z2 x2 y2 z 2 分
(0-2)+ 0=(0-2)+(0-2)+ 0= 0+ 0+(0-1), 9
( ) ( )
解得x y z 1 于是O 1 EC→ EO→ 1
0= 0=1,0= , 1,1, , =(2,2,-1), = 1,1,-
2 2 2
1EC→ 故由EO EC E可知CEO三点共线. 分
= , ∩ = , , 11
2
高二数学试题参考答案 第 页 共 页
【 6 ( 7 )】方法二 几何法 不妨记M 为EC中点 N为AC中点 显然有MN AC 而由EA AB MN EA知MN
: : , , ⊥ , ⊥ , ∥
AB 分
⊥ , 7
由AB AC AAB 平面ABCAC 平面ABC知MN 平面ABC. 分
∩ = , ⊂ , ⊂ ⊥ 8
由AB BC可知NB NA NC 易知有且仅有直线MN 上任一点到ABC的距离相
⊥ = = , , ,
等 故O MN 分
, ∈ , 9
同理EA AC可知过点M且垂直于平面AEC的直线l上任一点到AEC的距离相等 故O l 分
⊥ ,, , ∈ , 10
由l MN M 知点O即为点M 于是CEO三点共线. 分
∩ = , , , 11
注 采取方法二在 建系可得 分.建系过程在方法一已给出.
: (2)(ii) 1
以A为坐标原点 BC→的方向为x轴正方向 AB→的方向为y轴正方向 AP→的方向为z轴正方向 建立空
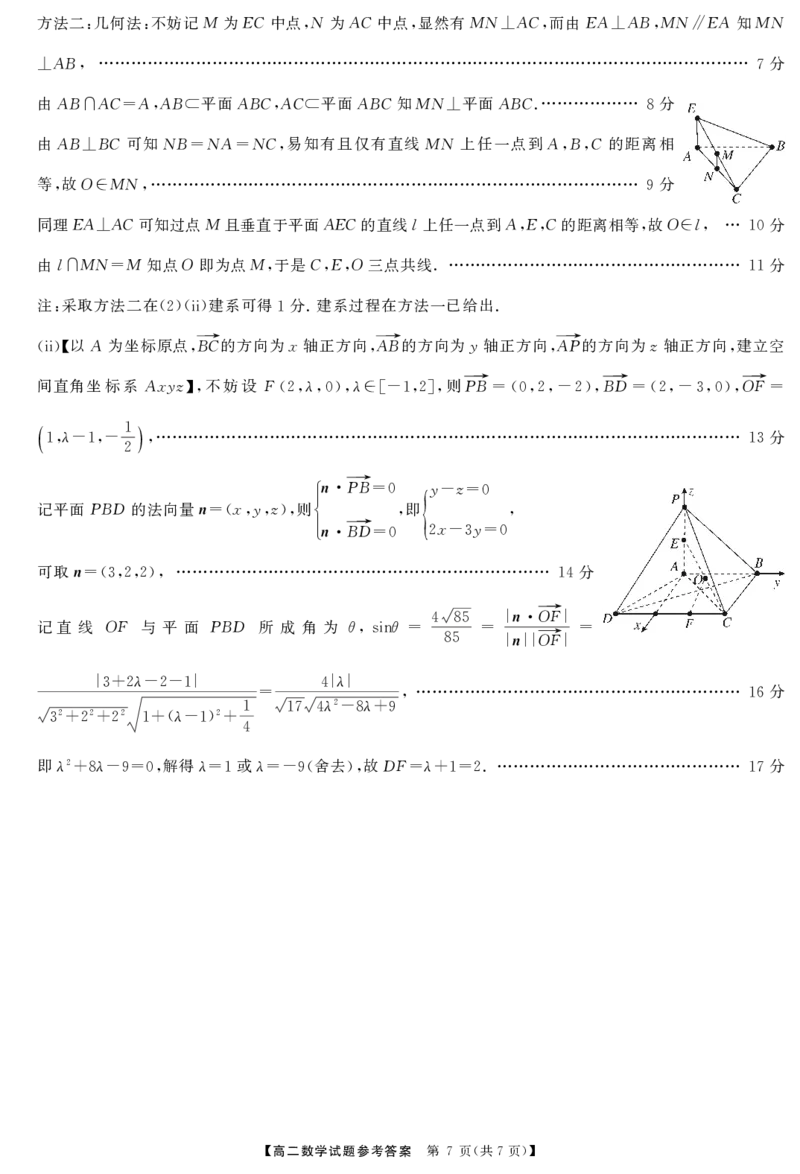
(ii)【 , , , ,
间直角坐标系Axyz 不妨设F λ λ 则PB→ BD→ OF→
】, (2,,0),∈[-1,2], =(0,2,-2), =(2,-3,0), =
( )
λ 1 分
1,-1,- , 13
2
ì ïï n
PB→
=0
{y
-
z
=0
记平面PBD的法向量n xyz 则í 即
=(,,), ïï , ,
în BD→ x y
=0 2 -3 =0
可取n 分
=(3,2,2), 14
n OF→
记 直 线 OF 与 平 面 PBD 所 成 角 为θ θ 4 85 | |
,sin = = n OF→ =
85 ||| |
λ λ
|3+2 -2-1| 4|| 分
= λ2 λ , 16
2 2 2 λ 2 1 17 4 -8 +9
3+2+2 1+(-1)+
4
即λ2 λ 解得λ 或λ 舍去 故DF λ . 分
+8 -9=0, =1 =-9( ), = +1=2 17
高二数学试题参考答案 第 页 共 页
【 7 ( 7 )】