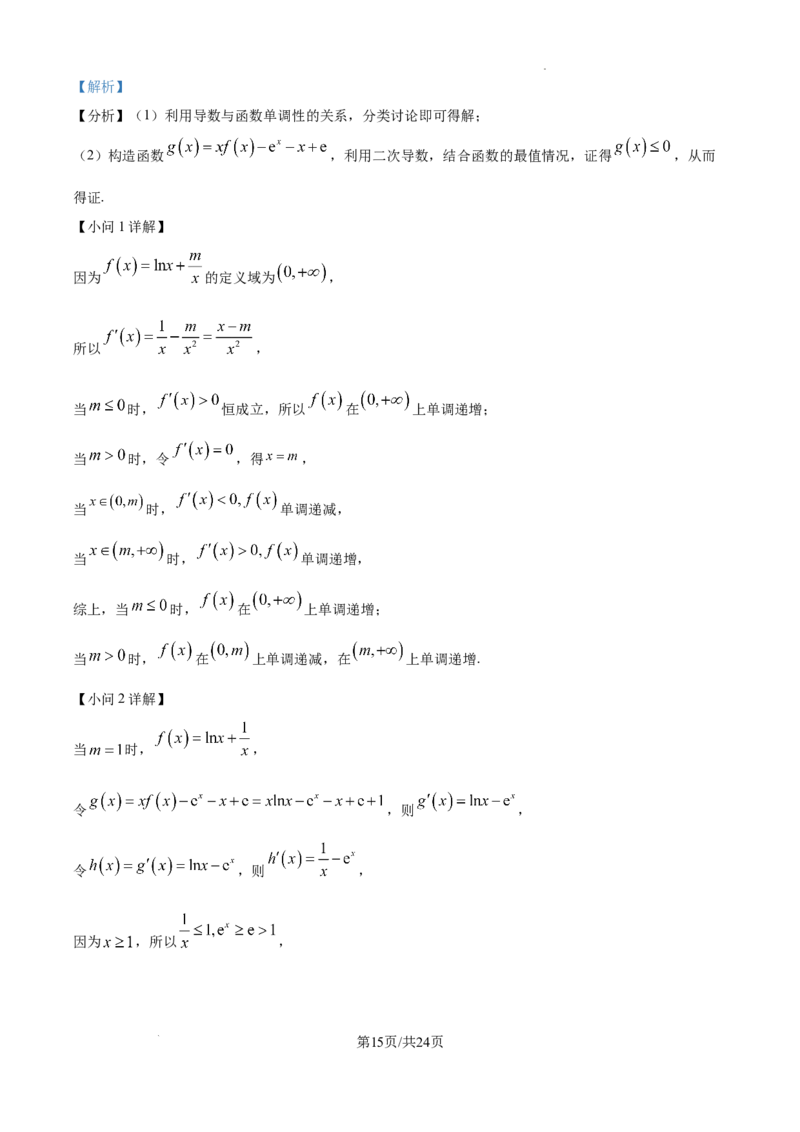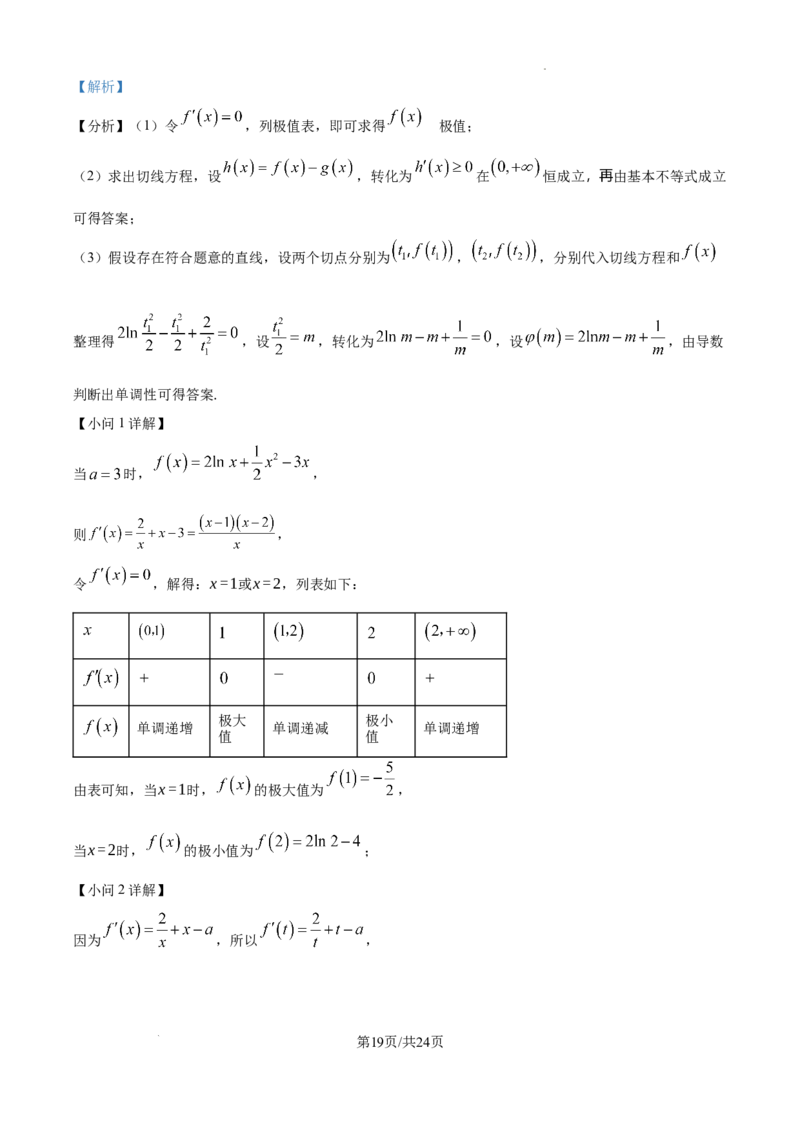文档内容
合肥市普通高中六校联盟 2024-2025 学年第一学期期中联考
高三年级数学试卷
(考试时间:120分钟 满分:150分)
命题学校:合肥三中 命题教师:蔡开根 审题教师:孟凡慧
一、单选题:本题共8小题,每小题5分,共计40分.每小题给出的四个选项中,只有一个选
项是正确的,请把正确的选项填涂在答题卡相应的位置上.
1. 已知 : , : ,若 是 的必要不充分条件,则实数 的取值
范围是( )
A. B. [2,+∞) C. D. (−∞,1]
【答案】D
【解析】
【分析】
解不等式确定集合 ,然后由必要不充分条件得 是 的真子集可得结论.
【详解】∵ 且 或 , ,又 是 的必要不
充分条件,∴ ,∴ ,
故选:D.
【点睛】结论点睛:本题考查由必要不充分条件求参数,一般可根据如下规则判断:
命题 对应集合 ,命题 对应的集合 ,则
(1) 是 的充分条件 ;
(2) 是 的必要条件 ;
(3) 是 的充分必要条件 ;
第1页/共24页
学科网(北京)股份有限公司(4) 是 的既不充分又不必要条件 集合 之间没有包含关系.
2. 已知集合 , ,则 ( )
A. B. C. D.
【答案】D
【解析】
【分析】根据偶次根下大于等于零,结合对数函数的单调性,可得集合 ;根据三角函数的性质可得集合
,结合交集的运算可得答案.
【详解】由题意 且 ,故 ,解得 ,故 ;
由 得 ,故 ;
综上 .
故选:D.
3. 已知 ,则( )
A. B. C. D.
【答案】C
【解析】
【分析】化对数式为指数式判断 ,判断 ,化指数式为对数式判断 ,则答案可求.
【详解】由 ,得 ;
由 ,得 ;
由 ,得 .
第2页/共24页
学科网(北京)股份有限公司∴ .
故选:C.
【点睛】本题考查指数式、对数式中的大小比较,一般可利用中介值 和函数单调性进行大小比较,是
基础题.
4. 已知函数 是 上的奇函数,且当 时, ,则当 时有( )
A. B.
C. D.
【答案】B
【解析】
【分析】根据函数的奇偶性,设 ,则 , ,再变形可得函数解析式.
【详解】解:设 ,则 ,
因为当 时,
又函数 是 上的奇函数
故当 时有
故选:
【点睛】本题考查函数的奇偶性,属于基础题.
5. 已知 ,则 ( )
A. B. C. D.
【答案】A
第3页/共24页
学科网(北京)股份有限公司【解析】
【分析】先由平方差公式化简已知条件并结合二倍角的余弦公式得 ,进而得 ,从而结合二倍角
正弦公式即可计算求解.
【详解】因为 ,
所以 ,
所以 ,即 ,
所以由 得 ,
所以 .
故选:A.
6. 若函数 的定义域为 ,则实数 取值范围是( )
A. B. C. D.
【答案】A
【解析】
【分析】分析可知, 在R上恒成立,分 、 两种情况讨论,在 时,直接
验证即可;在 时,可得出 ,综合可解得实数 的取值范围.
【详解】由题意,函数 的定义域为R,
等价于 在R上恒成立,
第4页/共24页
学科网(北京)股份有限公司若 ,则 在R上恒成立,满足条件;
若 ,则 ,解得 .
综上,实数 的取值范围是 ,
故选:A.
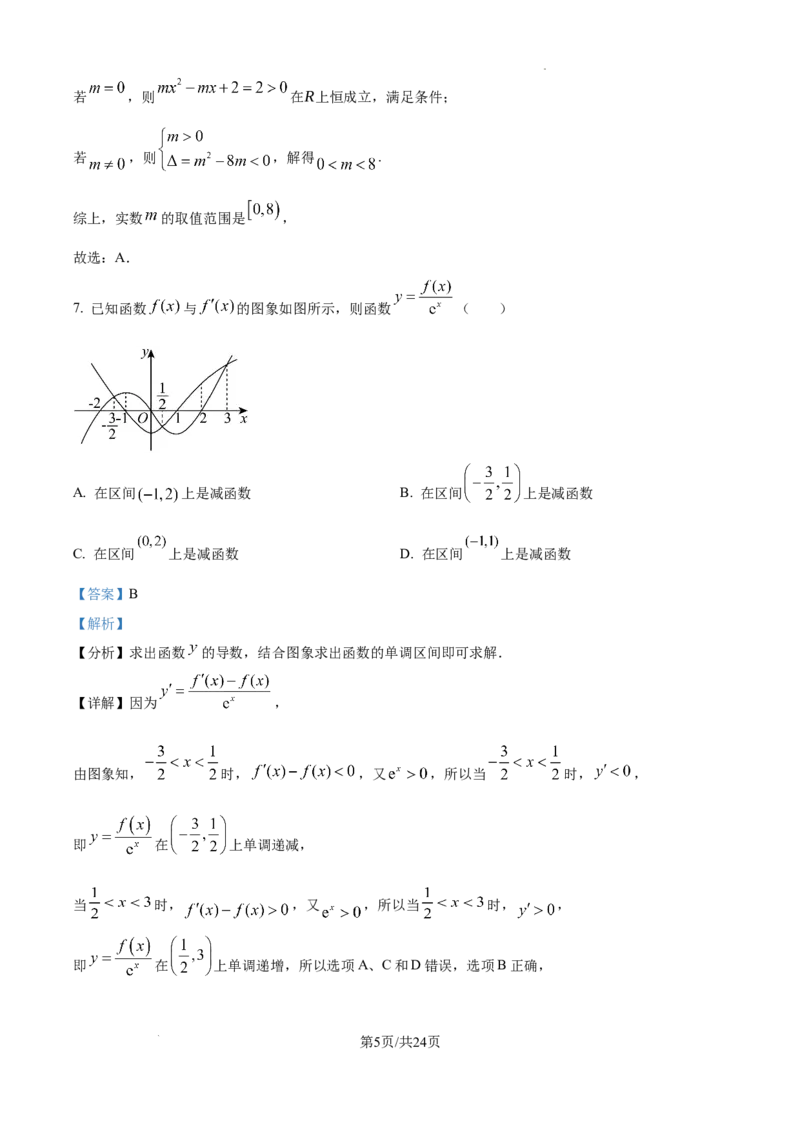
7. 已知函数 与 的图象如图所示,则函数 ( )
A. 在区间 上是减函数 B. 在区间 上是减函数
C. 在区间 上是减函数 D. 在区间 上是减函数
【答案】B
【解析】
【分析】求出函数 的导数,结合图象求出函数的单调区间即可求解.
【详解】因为 ,
由图象知, 时, ,又 ,所以当 时, ,
即 在 上单调递减,
当 时, ,又 ,所以当 时, ,
即 在 上单调递增,所以选项A、C和D错误,选项B正确,
第5页/共24页
学科网(北京)股份有限公司故选:B.
8. 定义:如果函数 在区间 上存在 ,满足 ,
,则称函数 是在区间 上的一个双中值函数,已知函数
是区间 上的双中值函数,则实数 的取值范围是
A. B. C. D.
【答案】A
【解析】
【详解】 ,
∵函数 是区间 上的双中值函数,
∴区间 上存在 ,
满足
∴方程 在区间 有两个不相等的解,
第6页/共24页
学科网(北京)股份有限公司令 ,
则 ,
解得
∴实数 的取值范围是 .
故选:A.
二、多选题:本题共3小题,每小题6分,共计18分.每小题给出的四个选项中,有多项符合
题目要求,全部选对的得6分,部分选对得部分分,有选错的得0分,请把正确的选项填涂
在答题卡相应的位置上.
9. 已知奇函数 的定义域为 ,若 ,则( )
A. B. 的图象关于直线 对称
C. D. 的一个周期为
【答案】AD
【解析】
第7页/共24页
学科网(北京)股份有限公司【分析】由奇函数可得 ,再根据函数的周期性与对称性分别判断.
【详解】由函数 为奇函数,则 ,A选项正确;
又 ,即 ,则函数 关于直线 对称,B选项错误;
由 可知 ,
即 ,函数 的一个周期为 ,C选项错误,D选项正确;
故选:AD.
10. 函数 满足 ,则正确的是( )
A. B.
C. D.
【答案】AC
【解析】
【分析】根据给定条件,构造函数 ,利用导数探讨单调,再比较大小即得.
【详解】依题意,令函数 ,求导得 ,函数 在R上递减,
对于A, , ,则 ,A正确;
对于B, , ,则 ,B错误;
对于C, , ,则 ,C正确;
对于D, , ,则 ,D错误.
故选:AC
第8页/共24页
学科网(北京)股份有限公司11. 已知 ,则( )
A. 的最小值为 B. 的最大值为
C. 的最小值为 D. 的最小值为
【答案】ABD
【解析】
【分析】根据指数运算,结合基本不等式即可判断 A;结合对数运算,利用基本不等式可判断 B;将
化为关于x的二次函数,结合二次函数性质可判断是C;通过变量代换,令 ,
得到 ,根据“1”的巧用,将 变形后,利用基本不等式,即可判断D..
【详解】对于A,由于 ,故 ,
当且仅当 ,结合 ,即 时,等号成立,
即 的最小值为 ,A正确;
对于B,由于 , ,则 ,
当且仅当 时,等号成立,
故 ,即 的最大值为 ,B正确;
对于C,又 ,得 ,
故
第9页/共24页
学科网(北京)股份有限公司由于 ,而 对称轴为 ,
则 在 上单调递减,在 上无最值,C错误;
对于D,令 ,则 ,
故 ,
由于 ,故 ,
,
则 ,
当且仅当 ,结合 ,即 时,等号成立,
所以 ,
即 的最小值为 ,D正确,
故选:ABD
【点睛】难点点睛:本题考查了基本不等式的应用,主要是求最值问题,难点是选项D的判断,解答时要
通过变量代换,令 ,得到 ,根据“1”的巧用,将 变形后,利
用基本不等式,即可求解.
三、填空题:本题共3小题,每小题5分,共15分.
12. 已知函数 对任意 满足 ,则 ______.
第10页/共24页
学科网(北京)股份有限公司【答案】
【解析】
【分析】采用方程组法消去 ,得出 的解析式即可.
【详解】因为 ,以 代替 得:
,
得: .
故答案为: .
13. 若函数 ,则使得 成立的 的取值范围是______.
【答案】
【解析】
【分析】由题知函数为偶函数且在 单调递增,由此抽象出不等式,解出即可
【详解】由函数的定义域为 ,
所以函数 为偶函数
当 时, 与 为单调递增函数
所以 在 单调递增
所以
所以
解得:
故答案为:
第11页/共24页
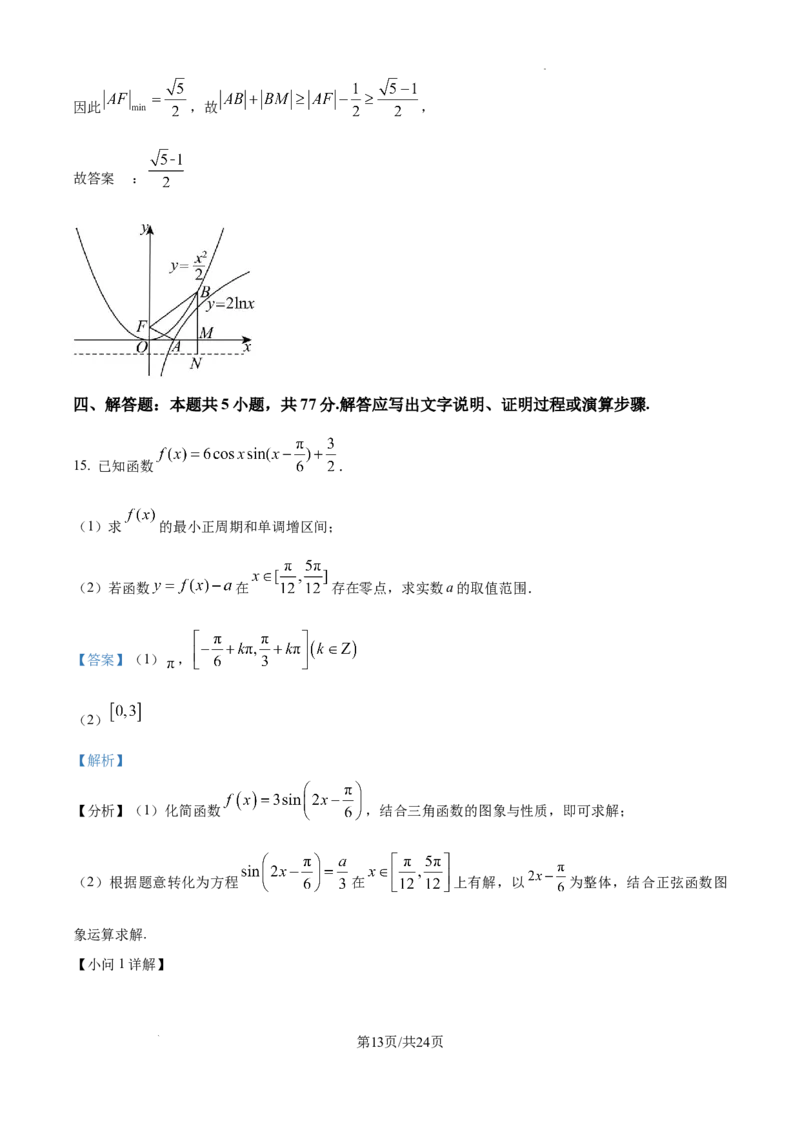
学科网(北京)股份有限公司14. 已知点A是函数 图象上的动点,点B是函数 图象上的动点,过B点作x轴的垂线,垂
足为M,则 的最小值为______.
【答案】
【解析】
【分析】根据抛物线的焦半径公式可将问题转化为 到 上一点 的最小距离即可,根据点点距
离公式,得 ,利用导数求解最小值即可.
【详解】由于 是焦点在 轴上的抛物线,故设其焦点为 ,
则 ,所以 ,
故求 到 上一点 的最小距离即可,
设 ,则 ,
记 ,则
由于函数 在(0,+∞)单调递增,且 ,
故当x∈(0,1)时 ,因此 在(0,1)单调递减,
当x∈(1,+∞)时 ,因此 在(1,+∞)单调递增,
故 ,
第12页/共24页
学科网(北京)股份有限公司因此 ,故 ,
故答案 :为
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15. 已知函数 .
(1)求 的最小正周期和单调增区间;
(2)若函数 在 存在零点,求实数a的取值范围.
【答案】(1) ,
(2)
【解析】
【分析】(1)化简函数 ,结合三角函数的图象与性质,即可求解;
(2)根据题意转化为方程 在 上有解,以 为整体,结合正弦函数图
象运算求解.
【小问1详解】
第13页/共24页
学科网(北京)股份有限公司对于函数
,
所以函数 的最小正周期为 ,
令 ,则 ,
∴函数 的单调递增区间为 .
【小问2详解】
令 ,即 ,则 ,
∵ 在 存在零点,则方程 在 上有解,
若 时,则 ,可得 ,
∴ ,得
故实数 的取值范围是 .
16. 已知函数 .
(1)讨论函数 的单调性;
(2)当 时,证明:当 时, .
【答案】(1)答案见解析
(2)证明见解析
第14页/共24页
学科网(北京)股份有限公司【解析】
【分析】(1)利用导数与函数单调性的关系,分类讨论即可得解;
(2)构造函数 ,利用二次导数,结合函数的最值情况,证得 ,从而
得证.
【小问1详解】
因为 的定义域为 ,
所以 ,
当 时, 恒成立,所以 在 上单调递增;
当 时,令 ,得 ,
当 时, 单调递减,
当 时, 单调递增,
综上,当 时, 在 上单调递增;
当 时, 在 上单调递减,在 上单调递增.
【小问2详解】
当 时, ,
令 ,则 ,
令 ,则 ,
因为 ,所以 ,
第15页/共24页
学科网(北京)股份有限公司所以当 时, 恒成立,所以 在 上单调递减,
即 在 上单调递减,所以 ,
所以 在 上单调递减,
所以 ,即 .
【点睛】结论点睛:恒成立问题:
(1) 恒成立 ; 恒成立 .
(2) 恒成立 ; 恒成立 .
(3) 恒成立 ; 恒成立 ;
(4) , , .
17. 在锐角 中,角A,B,C所对应的边分别为a,b,c,已知 .
(1)求角B的值;
(2)若 ,求 的周长的取值范围.
【答案】(1)
(2)
【解析】
【分析】(1)根据正弦定理得到 ,再利用余弦定理求出 ;
(2)根据正弦定理得到 ,从而得到 ,
第16页/共24页
学科网(北京)股份有限公司求出 ,得到 , ,从而求出周长的取值范围.
【小问1详解】
,由正弦定理得: ,
即 ,
由余弦定理得: ,
因为 ,
所以 ;
【小问2详解】
锐角 中, , ,
由正弦定理得: ,
故 ,
则
,
因为锐角 中, ,
则 , ,
第17页/共24页
学科网(北京)股份有限公司解得: ,
故 , ,
则 ,
故 ,
所以三角形周长的取值范围是 .
【点睛】解三角形中最值或范围问题,通常涉及与边长,周长有关的范围问题,与面积有关的范围问题,
或与角度有关的范围问题,
常用处理思路:①余弦定理结合基本不等式构造不等关系求出答案;
②采用正弦定理边化角,利用三角函数的范围求出最值或范围,如果三角形为锐角三角形,或其他的限制,
通常采用这种方法;
③巧妙利用三角换元,实现边化角,进而转化为正弦或余弦函数求出最值
18. 已知函数 , .
(1)若 ,求 的极值;
(2)设函数 在 处的切线方程为 ,若函数 是 上的单调增函
数,求 的值;
(3)函数 的图象上是否存在不同的两点,使得函数的图象在这两点处的切线重合,若存在则求出
的取值范围,若不存在则说明理由.
【答案】(1) 的极大值为 ,极小值为
(2)
在
(3)不存 ,理由见解析
第18页/共24页
学科网(北京)股份有限公司【解析】
的
【分析】(1)令 ,列极值表,即可求得 极值;
(2)求出切线方程,设 ,转化为 在 恒成立,再由基本不等式成立
可得答案;
(3)假设存在符合题意的直线,设两个切点分别为 , ,分别代入切线方程和
整理得 ,设 ,转化为 ,设 ,由导数
判断出单调性可得答案.
【小问1详解】
当 时, ,
则 ,
令 ,解得:x=1或x=2,列表如下:
极大 极小
单调递增 单调递减 单调递增
值 值
由表可知,当x=1时, 的极大值为 ,
当x=2时, 的极小值为 ;
【小问2详解】
因为 ,所以 ,
第19页/共24页
学科网(北京)股份有限公司所以 处切线方程为 ,
整理得: ,
设 ,则:
,
由题意可知,
恒成立.
在
因为 ,
当且仅当 时,等号成立,所以应有 ,
而 , ,所以只有 即 时, ,
即 成立,
所以 .
【小问3详解】
由(2)可知,曲线y=f(x)在 处切线方程为:
,
假设存在符合题意的直线,设两个切点分别为 , ,
第20页/共24页
学科网(北京)股份有限公司则: ,
由①式可得: ,代入②式,则: ,
整理得: ,
设 ,则 ,设 ,
则 ,
所以 单调递减,
因为 ,所以 的解为 .
即 ,解得 ,
此时 ,
所以不存在符合题意的两点,使得函数的图象在这两点处的切线重合.
【点睛】本题考查导数与函数的单调性与极值,切线问题,转化与化归能力,准确计算是关键,第三问转
化为函数与方程的关系是难点,是较难的题目.
19. 在平面直角坐标系 中,利用公式 ①(其中 , , , 为常数),将点P(x,y)
变换为点 的坐标,我们称该变换为线性变换,也称①为坐标变换公式,该变换公式①可由 , ,
, 组成的正方形数表 唯一确定,我们将 称为二阶矩阵,矩阵通常用大写英文字母 ,
第21页/共24页
学科网(北京)股份有限公司,…表示.
(1)在平面直角坐标系 中,将点 绕原点 按逆时针旋转 得到点 (到原点距离不变),
求点 的坐标;
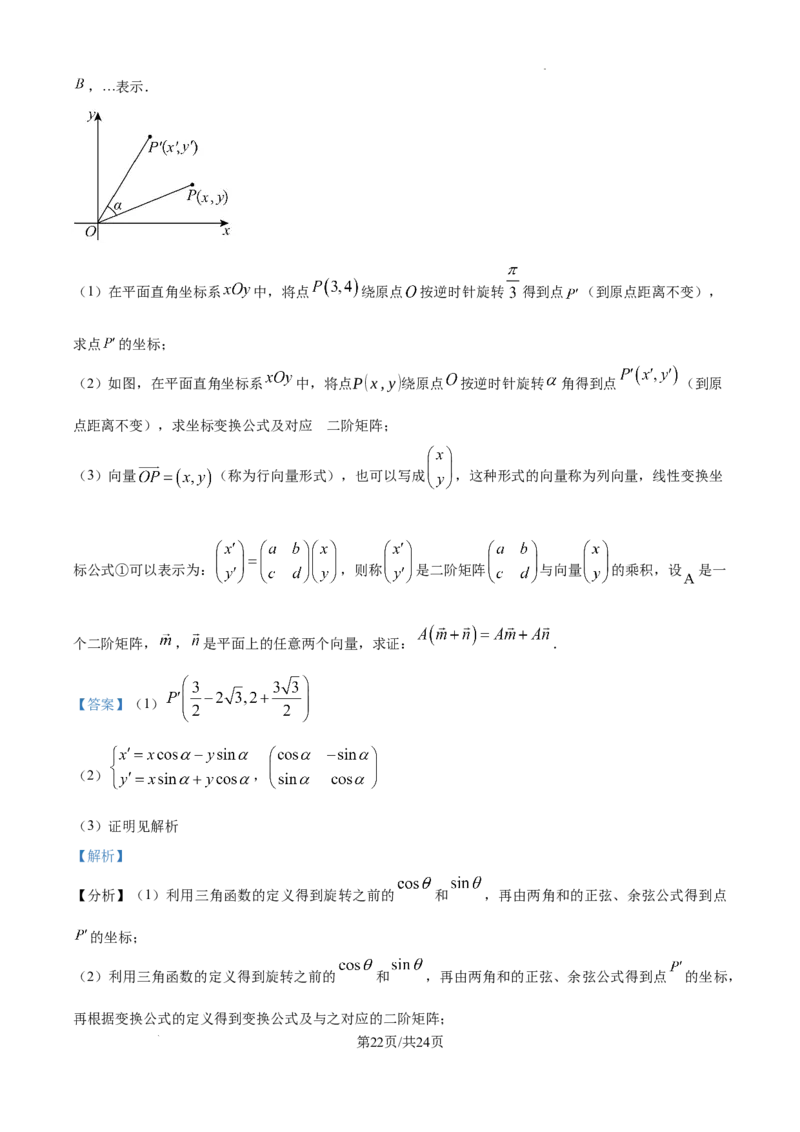
(2)如图,在平面直角坐标系 中,将点P(x,y)绕原点 按逆时针旋转 角得到点 (到原
点距离不变),求坐标变换公式及对应 的二阶矩阵;
(3)向量 (称为行向量形式),也可以写成 ,这种形式的向量称为列向量,线性变换坐
标公式①可以表示为: ,则称 是二阶矩阵 与向量 的乘积,设 是一
个二阶矩阵, , 是平面上的任意两个向量,求证: .
【答案】(1)
(2) ,
(3)证明见解析
【解析】
【分析】(1)利用三角函数的定义得到旋转之前的 和 ,再由两角和的正弦、余弦公式得到点
的坐标;
(2)利用三角函数的定义得到旋转之前的 和 ,再由两角和的正弦、余弦公式得到点 的坐标,
再根据变换公式的定义得到变换公式及与之对应的二阶矩阵;
第22页/共24页
学科网(北京)股份有限公司(3)根据定义分别计算 、 、 ,证明 即可.
【小问1详解】
可求得 ,设 ,则 , ,
设点 , ,
故
所以 .
【小问2详解】
设 , ,则 , , ,
故
所以坐标变换公式为 ,
该变换所对应的二阶矩阵为
【小问3详解】
设矩阵 ,向量 , ,则 .
,
第23页/共24页
学科网(北京)股份有限公司对应变换公式为: ,
,
所以
故对应变换公式同样为
所以 得证.
【点睛】方法点睛:利用三角函数的定义解题:(1)角 的顶点与坐标原点重合;(2)角的始边与 轴
正半轴重合;在角 的终边上任取一点 ,该点到原点的距离 ,则: ;
; .
第24页/共24页
学科网(北京)股份有限公司