文档内容
安徽省十校联盟2025-2026学年高二上学期12月月考
数学答案
1.A
2.B
3.C
4.A
5.D
6.A
7.C
8.D
9.AC
10.ACD
11.ABC
12.
13.
14.
15.(1)由 可知, , ,
联立两式 ,解得 ,故 ,
因此数列 的通项公式为 ;
(2)因为 ,
故 即 ,
解得 ,故 ,
即满足条件的 的值构成的集合为 .
16.(1)设 ,则 ,由题易知 ,即 .
.
因为点 均在椭圆上,故有 ,两式相减得 ,
整理得 ,因此 .
(2)联立直线 与椭圆方程, ,消去 ,整理得: ,
由韦达定理得, ,
由弦长公式,
1.
17.(1)设圆 的方程为 ,
由题意可得 ,解得 ,
所以圆 的方程为 ,即 ,
因为点 在直线 上,设 ,圆 的半径为 ,
则圆 的方程为 ,即 ,
因为圆 与圆 交于 , 两点,
故两圆相交即得相交弦所在直线方程,即 ,
因为直线 的方程为 ,即 ,
故系数比例相同,即 ,解得 , ,
所以圆 的方程为 ;
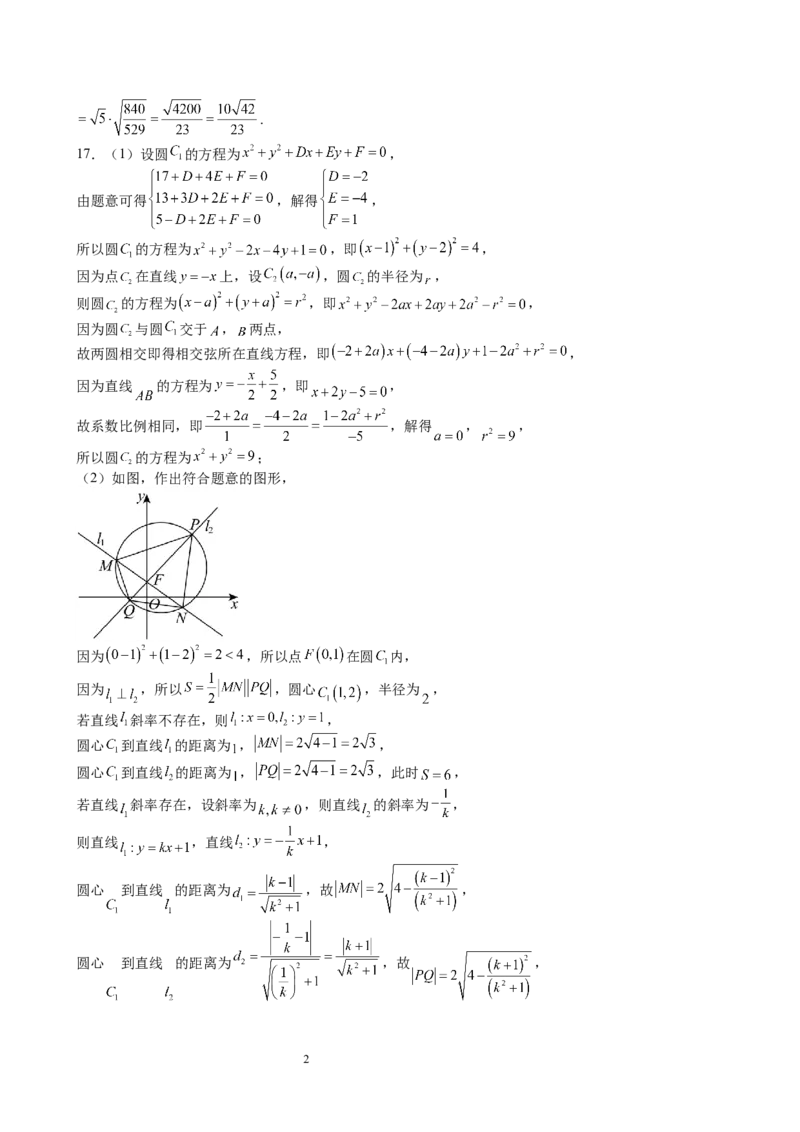
(2)如图,作出符合题意的图形,
因为 ,所以点 在圆 内,
因为 ,所以 ,圆心 ,半径为 ,
若直线 斜率不存在,则 ,
圆心 到直线 的距离为 , ,
圆心 到直线 的距离为 , ,此时 ,
若直线 斜率存在,设斜率为 ,则直线 的斜率为 ,
则直线 ,直线 ,
圆心 到直线 的距离为 ,故 ,
圆心 到直线 的距离为 ,故 ,
2所以 ,
化简可得 ,,
令 ,
当且仅当 时,即 时等号成立,
所以 ,即 ,
综上,四边形 面积 的取值范围为 .
18.(1)由题意得 ,令 ,则 ,
连接 ,作 ,则由矩形性质得 ,
因为平面 平面 , 面 ,所以 面 ,
如图,以 为原点,建立空间直角坐标系,
因为等边三角形 ,所以由勾股定理得 , ,
则 ,
得到 , , ,
设面 的法向量为 , ,
则 ,令 ,解得 ,
则面 的法向量为 ,
由题意得 在线段 上,则 ,可得 ,
而 ,则 ,解得 ,
则 ,得到 ,
因为 平面 ,所以 ,
则 ,解得 ,
此时 ,故 为线段 的中点.
(2)由题意得 在线段 上,则 ,
3由已知得 ,则 ,
设 ,则 ,
可得 ,解得 ,可得 ,
由已知得 ,则 ,
而 , ,
设面 的法向量为 ,
则 ,令 ,解得 ,
则面 的法向量为 ,
设直线 与平面 所成角为 , ,
则
,
则 ,
令 ,可将 化为 ,
令 ,由二次函数性质得 在 上单调递增,
则 最小值为 ,此时 取得最大值, ,
结合题意可得,当 取得最大值时, 也取得最大值,
则 最大值为 .
19(1)设双曲线 的方程: ,
将点 代入可得, ,解得 ,
故双曲线 的方程为 .
(2)(i)由题意知,直线 , 为圆 的两条切线,
4显然圆 的切线 ,即 的斜率存在,
设切线 ,由于切线 不平行于 的渐近线,则 ,
又圆心 到切线 的距离: ,则 ,
联立方程: ,消去 得 ,
由于 ,设 ,则 ,
而 ,
则 ,
即 ,故 .
(ii)由(i)同理可得, ,由于 三点共线,则 ,
设切线 与圆 的切点为 ,则 ,
故 ,
而
,
又 ,则 ,当 时, , ,
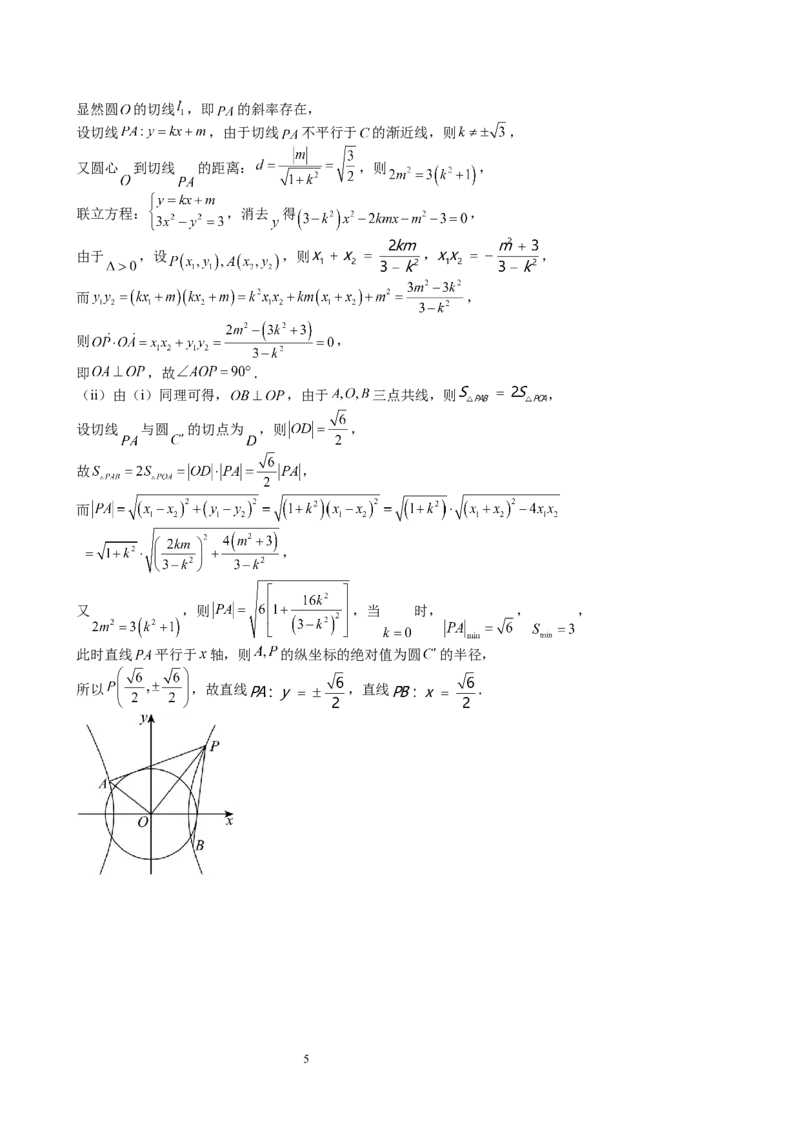
此时直线 平行于 轴,则 的纵坐标的绝对值为圆 的半径,
所以 ,故直线 ,直线 .
5