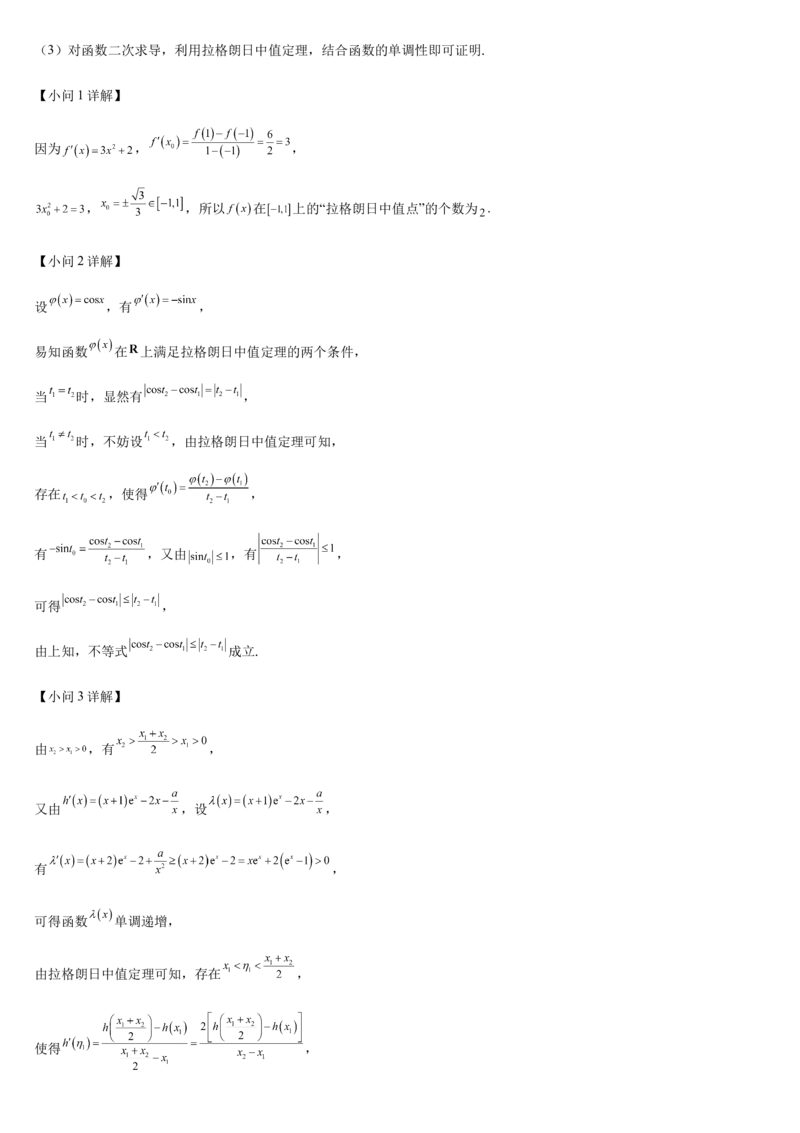文档内容
万州二中高 2023 级高二下期期中考试数学试题
注意事项:
1. 答题前,务必将自己的姓名、准考证号填写在答题卡规定的位置上.
2. 答选择题时,必须使用 2B 铅笔将答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦擦干净后,再选涂其他答案标号.
3. 答非选择题时,必须使用 0.5 毫米黑色签字笔,将答案书写在答题卡规定的位置上.
4. 所有题目必须在答题卡上作答,在试题卷上答题无效.
一、单选题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 的值为( A )
A 9 B 18 C 24 D 30
2.已知 是相互独立事件,且 ,则 ( )
A.0.1 B.0.12 C.0.18 D.0.28
【答案】C
【详解】由 可得 ,
又 是相互独立事件,所以 .
故选:C
3. 的二项展开式中 的系数为( )
A. 15 B. 6 C. D.
【详解】 的二项展开式为 ,
令 ,解得 ,
故所求即为 .
故选:B.
4.已知函数 , 是函数f(x)的导函数,则
A. 0 B. -1 C. 1 D.
,所以 ,故选A
5. 已知函数 有极值,则实数a的取值范围是( )A. B. C. D.
【答案】D
【解析】
【分析】原函数有极值等价于导函数有变号零点,对于二次函数即判别式 ,由此计算a的取值范围即可.
【详解】由 ,
得 ,
根据题意得 ,
解得 或 ,
所以实数a的取值范围是 .
故选:D.
6. 已知函数 ,若 在 上恒成立,则实数 的取值范围是( )
A. B. C. D.
【答案】B
【解析】
【分析】分析可知 ,利用导数求出函数 在 上的最大值,可得出关于实数 的不等式,解之即可.
【详解】因为 ,则 ,其中 ,
令 ,解得 ,令 ,解得 .
所以 在 上单调递减,在 上单调递增,
因为 , ,所以, ,
因为 在 上恒成立,所以, ,解得 .
故选:B
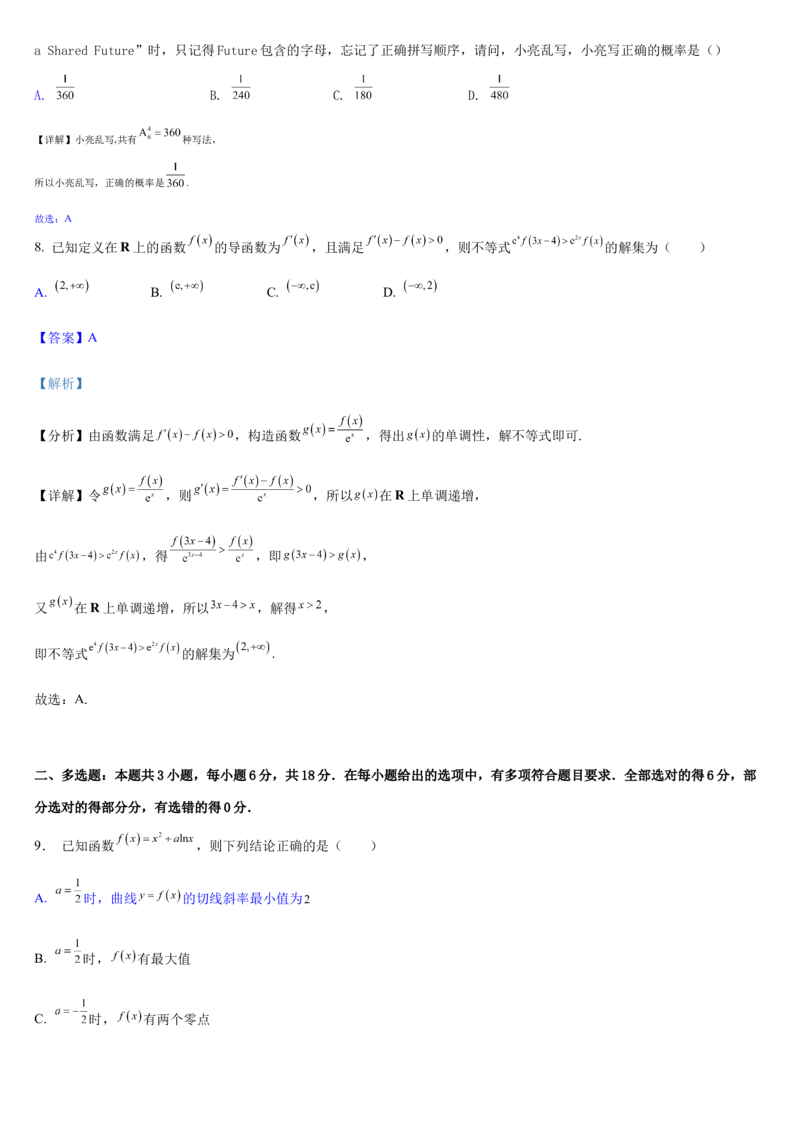
7.2022年北京冬奥会圆满结束,学校要求出一期有关于冬奥会的主题黑板报,小亮在书写本届冬奥会的主题“Together fora Shared Future”时,只记得Future包含的字母,忘记了正确拼写顺序,请问,小亮乱写,小亮写正确的概率是()
A. B. C. D.
【详解】小亮乱写,共有 种写法,
所以小亮乱写,正确的概率是 .
故选:A
8. 已知定义在R上的函数 的导函数为 ,且满足 ,则不等式 的解集为( )
A. B. C. D.
【答案】A
【解析】
【分析】由函数满足 ,构造函数 ,得出 的单调性,解不等式即可.
【详解】令 ,则 ,所以 在R上单调递增,
由 ,得 ,即 ,
又 在R上单调递增,所以 ,解得 ,
即不等式 的解集为 .
故选:A.
二、多选题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部
分选对的得部分分,有选错的得0分.
9. 已知函数 ,则下列结论正确的是( )
A. 时,曲线 的切线斜率最小值为
B. 时, 有最大值
C. 时, 有两个零点D. 时, 有最小值
【详解】函数 的定义域为 ,且 ,
对于A选项,当 时, ,
当且仅当 时,即当 时,等号成立,
所以, 时,曲线 的切线斜率最小值为 ,A对;
对于B选项,当 时, 对任意的 恒成立,
所以,当 时,函数 在 上为增函数,则 无最大值,B错;
对于CD选项,当 时, , ,
由 可得 ,由 可得 ,
此时,函数 的减区间为 ,增区间为 ,
则 ,所以, ,
所以,当 时,函数 有最小值,函数 无零点,C错D对.
故选:AD.
10.从7名男生和3名女生中选出4人去参加一项创新大赛,则下列说法正确的有( )
A.如果4人中男生女生各有2人,那么有63种不同的选法
B.如果男生中的甲和女生中的乙必须在内,那么有28种不同的选法
C.如果男生中的甲和女生中的乙至少要有1人在内,那么有140种不同的选法
D.如果4人中必须既有男生又有女生,那么有184种不同的选法
【答案】ABC【详解】对于A,如果4人中男生女生各有2人,男生的选法有 种,女生的选法有 种,所以共有
种不同的选法.故A正确.
对于B,如果男生中的甲和女生中的乙必须在内,在剩下的8人中再选2人即可,
有 种不同的选法,故B正确.
对于C,在10人中任选4人,有 种不同的选法,甲乙都不在其中的选法有 ,
故男生中的甲和女生中的乙至少要有1人在内的选法有 种,故C正确.
对于D,在10人中任选4人,有 种不同的选法,只有男生的选法有 种, 10
人中任选4人不可能全是女生,故4人中必须既有男生又有女生的选法有 种,故D错误.
故选:
11.已知 ,则( )
A. B.
C. D.
11.【答案】AD
【分析】结合图象和指、对函数之间的关系即可判断AB;利用切线不等式 即可判断C;利用不等式 即可判断
D.
【详解】对于A,
由图可知: 与 交点 ,
与 的交点 ,根据指数函数与对数函数为一对反函数知:A, 关于 对称,
故 , ,故A正确;
对于B,由A知 ,故B错误;
对于C,由 知 ,则 ,设 , ,
则 ,则当 时, ,此时 单调递减;
当 时, ,此时 单调递增;
则 ,则 恒成立,即 ,当 时取等;
令 ,则有 ,因为 ,则 ,即 ,故C错误;
对于D,设 , ,则 ,
则当 时, ,此时 单调递增;
当 时, ,此时 单调递减,
则 ,即 在 上恒成立,
即 在 上恒成立,当 时取等,
令 ,则 ,即 ,
因为 ,则 ,则 ,故 ,故D正确.
故选AD.
三、填空题:本题共3小题,每小题5分,共15分.
12.. 在 的展开式中, 的系数为__-120___
13.若 则它们的大小关系是(用小于符合,从左到右,从小到大的顺序排列)__________
14. 某城市的交通道路如图,从城市的西南角 到城市的东北角 ,经过城市中心广场 ,最近的走法种数有__________种.【答案】60
【解析】
【分析】解决本问题可以分为两步来解决,先查出A到 的走法,再查出 到 的走法,相乘即得答案.
【详解】用分步乘法原理解题,分两步,
第一步,由A到 ,共走5段路,3横5竖,共有 种走法;
第二步,由 到 ,共走4段路,2横2竖,共有 种走法
最近的走法种数有 种
故答案为:60
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.设 , ,已知
(1)求实数 的值;
(2)求 的值;
【答案】(1) ;
(2) ;
(3)128.
【详解】(1)根据二项式定理可得 ,
所以 ,解得 ;
(2)由(1)知 ,
令 得
再令 得
所以 ;
16.2024年3月22日是第三十二届“世界水日”,3月22日-28日是第三十七届“中国水周”.为了唤起孩子们的节约用水意
识,加强水资源保护,万州二中举办了关于“水资源”的问答比赛.比赛规则如下: 盒中有5个红球,4个白球, 盒中有5
个红球,5个白球(两盒中的球除颜色外其他都相同).现随机选择一盒,然后从中随机抽取2个球,若抽到球的颜色相同,
则回答第一类问题,答对得2分,若抽到球的颜色不同,则回答第二类问题,答对得3分,两类问题答错均不得分.甲同学参
加比赛.
(1) 求甲同学抽到 盒的概率
(2)求甲同学在一轮比赛中回答第一类问题的概率;【答案】(1)设事件 “抽到 盒”,事件 “抽到 盒”,
则 ,
“随机抽取两个球,颜色相同”,
, ,
由全概率公式得 ,
所以甲同学在一轮比赛中回答第一类问题的概率为 ;
17.某学校派出6名同学参加省教育厅主办的理科知识竞赛,分为数学竞赛,物理竞赛和化学竞赛,该校每名同学只能参加
其中一个学科的竞赛,且每个学科至少有一名学生参加.
(1)求该校派出的6名学生总共有多少种不同的参赛方案?
(2)若甲同学主攻数学方向,必须选择数学竞赛,乙同学主攻物理方向,必须选择物理竞赛,则这6名学生一共有多少种不同
的参赛方案?
【答案】(1)若参加三个学科的人数分别为1,1,4时,共有 种参赛方案;
若参加三个学科的人数分别为1,2,3时,共有 种参赛方案;
若参加三个学科的人数分别为2,2,2时,共有 种参赛方案;
该校派出的6名学生总共有 种不同的参赛方案.
(2)若有4人选择化学竞赛,则有1种参赛方案;
若有3人选择化学竞赛,余下的一人有2种选法,则有 种参赛方案;
若有2人选择化学竞赛,余下的两人各有2种选法,则有 种参赛方案;
若有1人选择化学竞赛,余下的三人各有2种选法,则有 种参赛方案;
所以总共有 种不同的参赛方案.18. 已知函数 有两个不同的零点 .
(1)求 的取值范围;
(2)求证: .
【答案】(1)
(2)证明见解析
【解析】
【分析】(1)求出 的导函数后分类讨论,发现只有 才可能存在两个不同的零点,求出函数 的单调性,则需
的极大值大于 才能满足题意,由此求出 的取值范围;
(2)由零点定义得到两个方程,变形得到两根之和的等式,通过构造函数证明所求不等式.
【
小问1详解】
由题意知函数 的定义域为 ,导函数为 ,
若 ,则 ,即 在 上单调递增,则 在 上至多一个零点,不合题意舍去;
则必有 ,令 ,得 ,
当 时, ;当 时, ,
所以 在 上单调递增,在 上单调递减,
故 存在极大值 ,无极小值.
因为当 时, ;当 时, ,
若函数 有两个不同的零点,则 ,解得 ,
所以 的取值范围为 .
【小问2详解】
因为 是函数 有两个不同的零点,不妨设 ,
则 ,
两边取对数得 ,两式相减得 ,
设 ,则 ,且有 ,解得 ,所以 ,
要证明 ,只需证明 ,即证 ,
故构造函数 ,则 ,
所以 在 上单调递减,所以 ,即 ,
故原不等式 成立.
19. 约瑟夫·路易斯·拉格朗日是闻名世界的数学家,拉格朗日中值定理就是他发现的.定理如下:若函数 满足如下条件:
①函数 在区间 上连续(函数图象没有间断);
②函数 在开区间 内可导(导数存在).则在区间 内至少存在一点 ,使得 成立,其中 称为“拉
格朗日中值点”.
(1)求函数 在 上的“拉格朗日中值点”的个数;
(2)对于任意的实数 , ,证明: ;
(3)已知函数 在区间 上满足拉格朗日中值定理的两个条件,当 时,证明:
.
【答案】(1)
(2)证明见解析 (3)证明见解析
【解析】
【分析】(1)先求 ,再根据“拉格朗日中值点” 的定义令 ,解方程即可求解;
(2)设 ,分 和 两种情况讨论,利用拉格朗日中值定理有 ,结合 即可求证;(3)对函数二次求导,利用拉格朗日中值定理,结合函数的单调性即可证明.
【小问1详解】
因为 , ,
, ,所以 在 上的“拉格朗日中值点”的个数为 .
【小问2详解】
设 ,有 ,
易知函数 在 上满足拉格朗日中值定理的两个条件,
当 时,显然有 ,
当 时,不妨设 ,由拉格朗日中值定理可知,
存在 ,使得 ,
有 ,又由 ,有 ,
可得 ,
由上知,不等式 成立.
【小问3详解】
由 ,有 ,
又由 ,设 ,
有 ,
可得函数 单调递增,
由拉格朗日中值定理可知,存在 ,
使得 ,同理可知,存在 ,
使得 ,
又由 和函数 单调递增,有 ,
有 ,
由 化简可得 ,
故不等式 成立.
【点睛】关键点点睛:本题关键在于能够将问题与拉格朗日中值定理联系并结合导数解决问题.