数学答案_2024-2025高二（7-7月题库）_2025年03月试卷_0330四川省南充市嘉陵一中2024-2025学年高二下学期3月月考试题

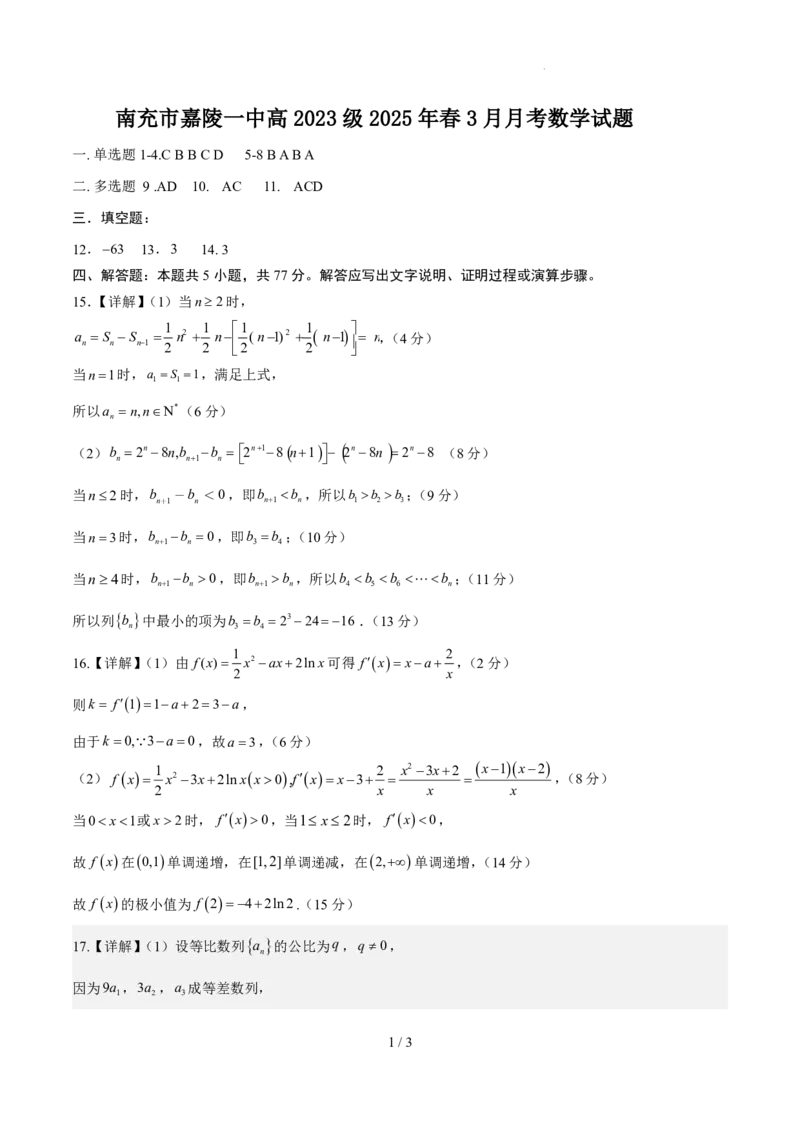
南充市嘉陵一中高 2023 级 2025 年春 3 月月考数学试题
一.单选题1-4.CBBCD 5-8BABA
二.多选题 9.AD 10. AC 11. ACD
三．填空题：
12．63 13．3 14.3
四、解答题：本题共5小题，共77分。解答应写出文字说明、证明过程或演算步骤。
15．【详解】（1）当n2时，
1 1 1 1 
a
n
S
n
S
n1

2
n2 
2
n
 2
(n1)2 
2
 n1
 
 n，（4分）
当n1时，a S 1，满足上式，
1 1
所以a n,nN*（6分）
n
（2）b
n
2n8n,b
n1
b
n
 

2n18n1

  2n8n  2n8 （8分）
当n2时，b -b <0，即b b ，所以b b b ；（9分）
n+1 n n1 n 1 2 3
当n3时，b b 0，即b b ；（10分）
n1 n 3 4
当n4时，b b 0，即b b ，所以b b b b ；（11分）
n1 n n1 n 4 5 6 n
所以列b 中最小的项为b b 232416．（13分）
n 3 4
1 2
16.【详解】（1）由 f(x) x2ax2lnx可得 fx xa ，（2分）
2 x
则k  f11a23a，
由于k 0,3a0，故a3，（6分）
1 2 x23x2 x1x2
（2） f x x23x2lnxx0,fxx3   ，（8分）
2 x x x
当0x1或x2时， fx0，当1 x2时， fx0，
故 f x在0,1单调递增，在[1,2]单调递减，在2,单调递增，（14分）
故 f x的极小值为 f 242ln2.（15分）
17.【详解】（1）设等比数列a 的公比为q，q0，
n
因为9a ，3a ，a 成等差数列，
1 2 3
1/3
学科网（北京）股份有限公司所以6a 9a a ，即6aq9a aq2，
2 1 3 1 1 1
化简可得q26q9q32 0，解得q3.
又a 1，
1
所以数列a 的通项公式为a 13n1 3n1.
n n
（2）因为b log a log 3n n，
n 3 n1 3
所以c 3a b n3n，
n n n
则S 131232333n3n，①，
n
3S 132233334Ln3n1，②
n
3
 13n
3 1 
①-②得2S 3132333nn3n1 n3n1   n 3n1 ，
n 13 2 2 
3 2n1
所以S   3n1.
n 4 4
a
18.解：（1）由题意可知x0,， fxlnx 1，
x
a 1 a xa
令gxlnx 1，则gx   ，
x x x2 x2
当a0时，gx0恒成立，gx单调递增，
当a0时，由gx0解得xa，由gx0解得0xa，
所以gx在a,单调递增，在0,a单调递减，
综上所述当a0时， fx单调递增，当a0时， fx在a,单调递增，在0,a单调递减.
（2）由（1）可知不等式xfx2xa即xlnxax2xa在1,上恒成立，
即axxlnx在1,上恒成立，只需axxlnx 即可，
max
令hxxxlnx，则hx1lnx1lnx，
当0x1时，hx0，hx单调递增，
当x1时，hx0，hx单调递减，
所以hx h11，所以a1.
max
2/3
学科网（北京）股份有限公司x2 a x2axa
19.【详解】（1）函数 f(x)alnx ax(a0)的定义域为(0,)，求导得 f(x) xa ，
2 x x
方程x2axa0中，a24a，（2分）
当0a4时，x2axa0恒成立， f(x)0， f(x)在(0,)上单调递增；
a a2 4a a a2 4a
当a4时，由x2axa0，解得x  0, x  ，
1 2 2 2
当0 x x 或xx 时， f(x)0；当x xx 时， f(x)0，
1 2 1 2
函数 f(x)在(0,x),(x ,)上单调递增，在[x ,x ]上单调递减，（5分）
1 2 1 2
所以当0a4时， f(x)的单调递增区间为(0,)；
a a24a a a24a
当a4时， f(x)的单调递增区间为(0, ),( , ) ，
2 2
a a2 4a a a2 4a
递减区间为[ , ].（7分）
2 2
（2）由（1）知， f(x)有两个极值点x ,x ，则a4,x x a,xx a，
1 2 1 2 1 2
1 1
f(x ) f(x )alnx  x2ax alnx  x2ax
1 2 1 2 1 1 2 2 2 2
1 1
aln(xx ) (x x )2xx a(x x )alna a2a，（13分）
1 2 2 1 2 1 2 1 2 2
1
令函数g(x) xlnx x2x,x4，求导得g(x)lnxx，令h(x)g(x),x4，
2
1
求导得h(x) 10，函数g(x)在(4,)上单调递减，g(x) g(4)ln440，
x
函数g(x)在(4,)上单调递减，g(x)g(4)4ln4128ln212，（16分）
所以 f(x ) f(x )8ln212.（17分）
1 2
3/3
学科网（北京）股份有限公司