四川省成都市树德中学2025届高三上学期10月月考数学试题扫描版含解析_2024-2025高三（6-6月题库）_2024年10月试卷_1013四川省成都市树德中学2025届高三上学期10月月考

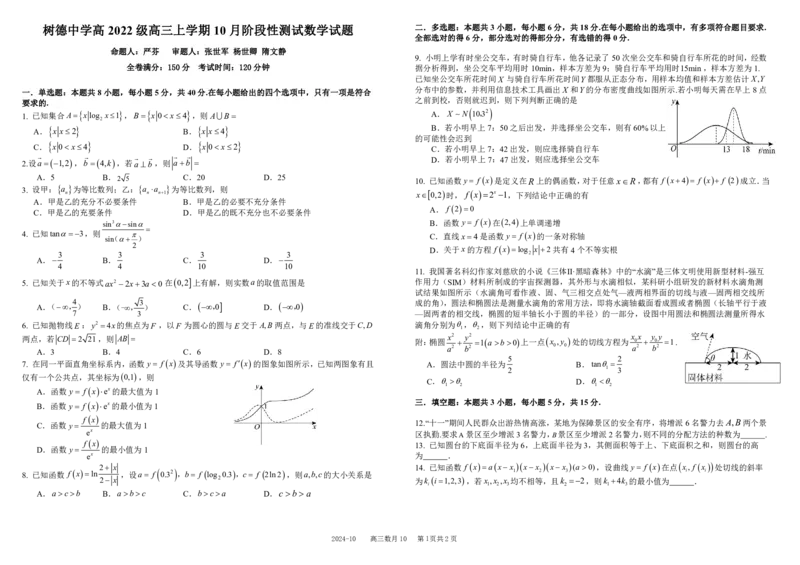
树德中学高 2022 级高三上学期 10 月阶段性测试数学试题 二．多选题：本题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项符合题目要求. 全部选对的得6分，部分选对的得部分分，有选错的得0分. 命题人：严芬 审题人：张世军 杨世卿 隋文静 9. 小明上学有时坐公交车，有时骑自行车，他各记录了50次坐公交车和骑自行车所花的时间，经数 全卷满分：150分 考试时间：120分钟 据分析得到，坐公交车平均用时10min，样本方差为9；骑自行车平均用时15min，样本方差为1. 已知坐公交车所花时间X 与骑自行车所花时间Y都服从正态分布，用样本均值和样本方差估计X,Y 一．单选题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合 分布中的参数，并利用信息技术工具画出X 和Y的分布密度曲线如图所示.若小明每天需在早上8点 之前到校，否则就迟到，则下列判断正确的是 要求的.   1. 已知集合A x log x1  ，B  x 0x4  ，则AB A．X  N 10，32 2 A．  x x2  B．  x x4  B．若小明早上7：50之后出发，并选择坐公交车，则有60%以上 的可能性会迟到     C． x 0x4 D． x 0x2 C．若小明早上7：42出发，则应选择骑自行车 2.设a  1,2，b  4,k，若a  b  ，则 a  b   D．若小明早上7：47出发，则应选择坐公交车 A．5 B． 2 5 C．20 D．25 10. 已知函数y f x是定义在R上的偶函数，对于任意xR，都有 f x4 f x f 2成立．当 3. 设甲：a n 为等比数列；乙：a n a n1 为等比数列，则 x 0,2时， f x2x1，下列结论中正确的有 A．甲是乙的充分不必要条件 B．甲是乙的必要不充分条件 C．甲是乙的充要条件 D．甲是乙的既不充分也不必要条件 A． f 20 sin3sin B．函数y f x在2,4上单调递增  4. 已知tan3，则 sin（  ） C．直线x4是函数y f x的一条对称轴 2 D．关于x的方程 f xlog x 2共有4个不等实根 3 3 3 3 2 A． B． C． D． 4 4 10 10 11. 我国著名科幻作家刘慈欣的小说《三体Ⅱ·黑暗森林》中的“水滴”是三体文明使用新型材料-强互 5. 已知关于x的不等式ax2 2x3a0在 0,2 上有解，则实数a的取值范围是 作用力（SIM）材料所制成的宇宙探测器，其外形与水滴相似，某科研小组研发的新材料水滴角测 试结果如图所示（水滴角可看作液、固、气三相交点处气—液两相界面的切线与液—固两相交线所 A．（， 4 ） B．（-， 3 ） C．，0  D．，0 成的角），圆法和椭圆法是测量水滴角的常用方法，即将水滴轴截面看成圆或者椭圆（长轴平行于液 7 3 —固两者的相交线，椭圆的短半轴长小于圆的半径）的一部分，设图中用圆法和椭圆法测量所得水 6. 已知抛物线E：y2 4x的焦点为F ，以F 为圆心的圆与E交于A,B两点，与E的准线交于C,D 滴角分别为，，则下列结论中正确的有 1 2 两点，若 CD 2 21，则 AB  附：椭圆 x2  y2 1a b 0上一点x ,y 处的切线方程为 x 0 x  y 0 y 1. A．3 B．4 C．6 D．8 a2 b2 0 0 a2 b2 5 2 7. 在同一平面直角坐标系内，函数y f x及其导函数y fx的图象如图所示，已知两图象有且 A．圆法中圆的半径为 B．tan  2 1 3 仅有一个公共点，其坐标为0,1，则 C．  D．  1 2 1 2 A．函数y f  x ex的最大值为1 B．函数y f  x ex的最小值为1 三．填空题：本题共3小题，每小题5分，共15分. C．函数y f x 的最大值为1 12.“十一”期间人民群众出游热情高涨，某地为保障景区的安全有序，将增派6名警力去A,B两个景 ex 区执勤.要求A景区至少增派3名警力，B景区至少增派2名警力，则不同的分配方法的种数为 . f x 13. 已知圆台的下底面半径为6，上底面半径为3，其侧面积等于上、下底面积之和，则圆台的高 D．函数y 的最小值为1 ex 为 ． 2 x 14. 已知函数 f xaxx xx xx (a0)，设曲线y f x在点  x, f x  处切线的斜率 8. 已知函数 f xln ，设a f  0.32  ，b f log 0.3，c f 2ln2，则a,b,c的大小关系是 1 2 3 i i 2 x 2 为k i1,2,3，若x,x ,x 均不相等，且k 2，则k 4k 的最小值为 ． i 1 2 3 2 1 3 A．acb B．abc C．bca D．cba 2024-10 高三数月10 第1页共2页四．解答题：本题共5小题，共77分.解答应写出文字说明、证明过程或演算步骤. 18.(17分) 15.(13分) 已知函数 f xx22xalnx ，aR . 在ABC中，角A,B,C的对边分别为a,b,c，且满足2bcsinA 3  a2c2b2 ． (1)若a1，求函数 f x在点  1, f 1 处的切线； (1)求B的大小； (2)若对任意的x 1 ,x 2 0,，x 1  x 2 ，有x 1 x 2  x 2 f x 1 x 1 f x 2   0恒成立，求实数a的取值 9 3 (2)若b3，ABC的面积为 ，求ABC的周长． 范围. 4 16.(15分) x2 y2 3 已知椭圆C:  1(ab0)经过点E（1, ）,P为椭圆C 的右顶点，O为坐标原点，OPE的面 a2 b2 2 3 积为 . 19.(17分) 2 2023年10月11日，中国科学技术大学潘建伟团队成功构建255个光子的量子计算机原型机“九章三 (1)求椭圆C的标准方程; 号”，求解高斯玻色取样数学问题比目前全球最快的超级计算机快一亿亿倍.相较传统计算机的经典比 (2)过点D(1,0)作直线l与椭圆C 交于A,B,A关于原点O的对称点为C ，若|BA|=|BC|，求直线AB 特只能处于0态或1态，量子计算机的量子比特（qubit）可同时处于0与1的叠加态，故每个量子 的斜率. 比特处于0态或1态是基于概率进行计算的.现假设某台量子计算机以每个粒子的自旋状态作为量子 比特，且自旋状态只有上旋与下旋两种状态，其中下旋表示“0”，上旋表示“1”，粒子间的自旋状态 相互独立.现将两个初始状态均为叠加态的粒子输入第一道逻辑门后，粒子自旋状态等可能的变为上 旋或下旋，再输入第二道逻辑门后，粒子的自旋状态有 p的概率发生改变，记通过第二道逻辑门后 的两个粒子中上旋粒子的个数为X . 1 (1)已知p ，求两个粒子通过第二道逻辑门后上旋粒子个数为2的概率； 3 (2)若一条信息有n  n1,nN* 种可能的情况且各种情况互斥，记这些情况发生的概率分别为p ， 1 17.(15分) p ，…，p ，则称H  f p  f p  f p （其中 f xxlog x）为这条信息的信息熵.试 2 n 1 2 n 2 如图，在四棱锥QABCD中，四边形ABCD为直角梯形，CD//AB，BC AB，平面QAD平面ABCD， 求两个粒子通过第二道逻辑门后上旋粒子个数为X 的信息熵H ； QAQD，点M 是AD的中点. (3)将一个下旋粒子输入第二道逻辑门，当粒子输出后变为上旋粒子时则停止输入，否则重复输入第 (1)证明：QM BD. 二道逻辑门直至其变为上旋粒子，设停止输入时该粒子通过第二道逻辑门的次数为 42 Y (Y 1,2,3,,n,)，证明：当n无限增大时，Y 的数学期望趋近于一个常数. (2)点N 是CQ的中点，AD AB2CD2，当直线MN与平面QBC所成角的正弦值为 时，求 7 参考公式：0q1时， lim qn 0， lim nqn 0. n n QM的长度． 2024-10 高三数月10 第2页共2页树德中学高 2022 级高三上学期 10 月阶段性测试数学试题 故y fxex  f xex  fx f xex 0恒成立， 故y f xex在R上单调递增，则A，B显然错误， 参考答案 f(x)ex f(x)ex f(x) f(x) 对于C，D，y  ex2  ex ， 一．单选题：1-8 CAACBDCC 二．多选题：9-11 ACD AC AD 由图像可知x(,0)，y f(x) f(x) 0恒成立，故y f(x) 单调递增， 三．填空题 12-14 35 4 18 ex ex 1. 【答案】C【详解】由log 2 x1，则log 2 xlog 2 2，所以0x2， 当x(0,)，y f(x) f(x) 0，y f(x) 单调递减， 所以A x log 2 x1  x 0 x2  ，AB   x 0 x 4  故选：C f(x) ex ex f 0 2.【答案】A【详解】a  1,2，b  4,k，若a  b  ，则有a  b  142k 0，解得k 2， 所以函数y ex 在x0处取得极大值，也为最大值， e0 1，C正确，D错误.故选：C 则有a  b  1,24,2 3,4，得 a  b   3242 5.故选：A 8. 【答案】C【详解】解：函数 f  x ln 2 x ， 由 2 x 0，即(x 2)(x 2)0， x 2 2 x 2 x 3. 【答案】A【详解】充分性：若a 为等比数列，设其公比为q， a a a n 解得x2,2  显然 f x  f  x  ，∴ f x为偶函数， 则 n n1  n1  q2，所以a a 为等比数列，公比为q2，满足充分性. a n1 a n a n1 n n1 ∴当x 0,2  时， f  x ln 2x 在x 0,2  单增， 必要性：若a a 为等比数列，公比为2， 2x n n1 a a a  f  x  在 2，0  上为减函数，在  0，2 上为增函数 则 n n1 2，即 n1 2， a n1 a n a n1 a 0.32 0.32 0，1  ， log 0.3 log 0.3log 10 log 2 3 2  3 假设a 为等比数列，此时 n1 q2 2无解，故不满足必要性. 2 2 2 3 2 2 n a n1 10 3  3 3  3 所以甲是乙的充分不必要条件.故选：A 所以 log 0.3 log   ,2 2ln2 ln4lne2  ， 2ln2  1，  4. 【答案】C【详解】因为tan3， 2 2 3 2  2  2 则 sin3  si  n   sin3 co  s sin   sin21  sin  sincos  tan  3 .故选：C. ∴ 二． b 多 c 选  题 a． ： 故 本 选 题 ： 共 C 3 ． 小题，每小题6分，共18分.在每小题给出的选项中，有多项符合题目要求. sin  cos cos2sin2 1tan2 10 全部选对的得6分，部分选对的得部分分，有选错的得0分.  2 9. 【答案】ACD【详解】由题意知，X ~ N  10,32 ，Y ~ N  15,12 ,A正确。 2x 2 5. 【答案】B【详解】当x0,2 时，由ax22x3a0可得 a x23  3 ， 对于B，若小明早上7：50之后出发，并选择坐公交车，有50%以上的可能性会超过10min，即8 x x 点之后到校会迟到，故B错误； 2 2 3 对于C、D，由题中的图可知，P  X 18 P  Y 18  ,P  X 13 P  Y 13  , 应选择在给定的   3 由基本不等式可得 x 3 2 x 3 3 ，当且仅当x 3时，等号成立，故a 3 .故选：B. 时间内不迟到的概率大的交通工具，所以小明早上7：42出发，有18min可用，则应选择骑自行车， x x 故C正确；小明早上7：47出发，有13min可用，则应选择坐公交车，故D正确； 6. 【答案】D【详解】由抛物线方程知： p 1，F1,0， 故选：ACD. 2 10. 【答案】AC【详解】由 f x4 f x f 2， 不妨设点A在第一象限，如图所示，直线CD与x轴交于点E， 令x2，则 f 2 f 2 f 2，即 f 20， 由 CD 2 21，则 ED  21,EF 2， 因为 f x是定义在R上的偶函数，所以 f 2 f 20，故A正确；  2 圆的半径r 21 22 5，所以 AF 5， 由A知， f 20，则 f x4 f x， 由抛物线的定义可得：x  p 5，所以x 4， 所以函数 f x是周期为4的偶函数，结合x 0,2时， f x2x1， A 2 A 画出大致图象如下： 又因为点A在抛物线上，所以A4,4，  AB 248．故选：D. 7. 【答案】C【详解】AB选项，由题意可知，两个函数图像都在x轴上方，任何一个为导函数， 则另外一个函数应该单调递增，判断可知，虚线部分为y fx，实线部分为y f x， 2024-10 高三数月10 第3页共2页结合图象可知，函数y f x在2,4上单调递减，直线x4是函数y f x的一条对称轴，故B错 1 1 1 由k 2，得   ， 误，C正确； 2 k 1 k 3 2 对于D，画出函数ylog x 2的大致图象如下： 由k 2，即k ax x x x 0，知x 位于x,x 之间， 2 2 2 2 3 2 1 2 1 3 不妨设x  x  x ，则k 0,k 0， 1 2 3 1 3  1 1   k 4k   k 4k  故k 4k 2k 4k    25 1 32 52 1 3 18 ， 1 3 1 3 k 1 k 3   k 3 k 1    k 3 k 1   k 4k 1  3 结合图象可知，函数y f x和ylog x 2有两个交点，  k k 2 当且仅当 3 1 ，即k 6,k 3时等号成立， 所以方程 f xlog 2 x 2共有2个不等实根，故D错误.故选：AC. 1  1  1 1 3 11. 【答案】AD【详解】由题意知，若将水滴轴截面看成圆的一部分，圆的半径为R，如图所示，  k 1 k 3 2 5 2 4 故则k 4k 的最小值为18，故答案为：18 则R2 (R1)24，解得R ，所以tan   ，若将水滴轴截面看成椭圆 1 3 2 1 R1 3 x2 y2 四．解答题：本题共5小题，共77分.解答应写出文字说明、证明过程或演算步骤. 的一部分，设椭圆方程为  1(ab0)，如图所示， a2 b2 15. (13分)解：（1）因为2bcsinA 3  a2 c2 b2 ，可得 2bcsinA  3 a2 c2b2 ， 则切点坐标为(2,b1)， 2ac 2ac 则椭圆 x2  y2 1上一点(2,b1)的切线方程为 2x  (b1)y 1， 由余弦定理得bsinA 3acosB，又由正弦定理得sinBsinA 3sinAcosB， a2 b2 a2 b2 π 因为0 Aπ，所以sinA0，所以sinB 3cosB，所以tanB 3，又因为0Bπ，所以B . 2b2 3 所以椭圆的切线方程的斜率为k tan  ， 2 2 a2(b1) 1 9 3 （2）由三角形的面积公式，可得S  acsinB ，可得ac9， 4 (b1)2 4b2 2 4 将切点坐标(2,b1)代入切线方程可得  1，解得 2b1， a2 b2 a2 又由余弦定理得b2 a2c22accosB(ac)23ac， 1 因为b3，所以(ac)2 b23ac93936，解得ac6，所以VABC的周长为abc9． (2b1) 5 所以 2b2 2 1 1 ，又因为bR ， tan    (2 ) 2 a2(b1) b1 2 b1 2 3 1 3 3  3 所以tan 2  1 2 (2 b 1 1 ) 4 3 tan 1 ，即tan 2 tan 1 ，所以 1  2 .故选：AD. 16. (15分)解：（1）因为OPE的面积为 2 ，则有 2 a 2  2 ，解得a2，又因为E   1, 2    1 3 x2 在椭圆C上，则  1，解得b1， 所以椭圆C的标准方程为 y2 1; 三．填空题：本题共3小题，每小题5分，共15分. 4 4b2 4 12.【答案】35【详解】由题意可知分两种情况：①A景区增派3名警力，B景区增派3名警力，则 （2）如图： 有C3 20种方法，②A景区增派4名警力，B景区增派2名警力，则有C4 15种方法， 因为|BA||BC|,O为AC的中点，所以OAOB，设 ， 6 6 所以由分类加法原理可知共有201535种方法.故答案为：35 x24y2 4 设直线的方程xmy1，并与椭圆的方程进行联立，可得 t ， 13.【答案】 【详解】设圆台的母线长为l，则圆台上底面面积S 32 9，  xmy1 1 圆台下底面面积S 2 62 36，所以两底面面积之和为45， 消去x得  m24  y22my30，则有y  y  2m ,y y  3 ， 又圆台侧面积S (36)l 9l ，则9l 45，所以l 5，   1 2 m24 1 2 m24 因为OAOB，则有OAOB0，则xx  y y 0，即 所以圆台的高为 l2  63 2 4.故答案为：  m21  y y my  y 10， 1 2 1 2 1 2 1 2 14.【答案】18【详解】由于 f xaxx xx xx (a0)， 故 fxa  xx 1 xx 2 xx 2 xx 3  1 xx 3 2 xx 1 3   ，  m21   m2 3 4 m m 2 2 m 4 10，即 1 m  2 4  m 4 2 0，解得m 1 2 ，所以直线AB的斜率为2. 故k ax x x x ,k ax x x x ，k ax x x x ， 1 1 2 1 3 2 2 3 2 1 3 3 1 3 2 17.(15分)解：（1）M是AD中点，QAQD，QM  AD， 1 1 1 1 1 1 则      平面QAD平面ABCD，平面QAD平面ABCDAD，QM 平面QAD， k k k ax  x  x  x a x  x x  x a x  x x  x 1 2 3 1 2 1 3 2 3 2 1 3 1 3 2 QM 平面ABCD，又BD平面ABCD，QM BD. x x x x x x  3 2 1 3 2 1 0， （2）方法一：取BC中点F，连接MF,QF ，作MGQF，垂足为G，连接NG,MC， ax x x x x x 1 2 2 3 3 1 M,F 分别为AD,BC中点，AB//CD，MF//AB，又BC AB，MF BC； 2024-10 高三数月10 第4页共2页由（1）知：QM 平面ABCD，BC平面ABCD，QM BC； ①若a0，Gx0恒成立，符合题意. QM,MF 平面QMF ，QM MF M ，BC平面QMF ， 1 lnx1 ②若a0，则  恒成立. MG平面QMF ，BCMG， a x2 又MGQF，QFBCF，QF,BC平面QBC，MG平面QBC， 令Fx lnx1 ，则Fx 32lnx ，令Fx 32lnx 0，则 3， 42 x2 x3 x3 0xe2 直线MN与平面QBC所成角为MNG，sinMNG ， 设QM aa0， 7 所以 在    0,e 3 2    单调递增，在    e 3 2,    单调递减，所以 1 a F    e 3 2     2 1 e3 ，所以a  0,2e3  . MF  1 ABCD 3 ，BC  AD2   1 AB   2  3， ③若a <0 ，同理， 1 a  lnx x2 1 恒成立，由②可知，当x0时，Fx，所以不存在满足条件的 2 2 2  a.综上所述，a0,2e3.   1  2 1 1 MC MF2 BC  3，MN  QC a23，  f x  f x  2  2 2 法二：x 1 x 2  x 2 f x 1 x 1 f x 2   0x 1 x 2   x 1  x 2   0， 3 3a 1 2 又MG  QM MF  2 a  3a ，sinMNG MG  94a2  42 ，解得：a 3或 令gx f x x2a lnx ，则只需gx在 单调递增，即gx0恒成立； QF 9 94a2 MN 1 7 x x a2 a23 4 2 a1lnx x2a1lnx m∞ gx1  ， 3 3 x2 x2 a ，故QM的长为 3 或 。 2 2 令hxx2a1lnx，则hx0恒成立；又hx2x a  2x2a ， 方法二：取BC中点F，连接MF， x x M,F 分别为AD,BC中点，AB//CD，MF//AB，又BC AB，MF BC；由（1）知：QM  ①当a0时，hxx2， 在 单调递增成立；   平面ABCD，以F 为坐标原点，FM,FB正方向为x,y轴正方向，过F 作z轴//QM ，可建立如图所 ②当a<0时， ， 在 单调递增， 示空间直角坐标系，设QM aa0， 又当x0时， hx ， 故h x  m  ∞ 0不恒成立，不满足题意； m∞ MF  1 ABCD 3 ，BC  AD2   1 AB   2  3， ③当a0时，由 得x a ， 2 2 2  2 3  3   3   3  3 3 a  a   a  M ,0,0，Q ,0,a，B  0, ,0  ，C  0, ,0  ，N  , ,   ， 则 在  0,   单调递减，在  ,  单调递增， 2  2   2   2  4 4 2  2   2  M  N        3 4 , 4 3 , 2 a    ，  B  C    0, 3,0  ，C  Q       3 2 , 2 3 ,a     ； 因为 h x0恒成立，所以h(x) min h     a 2      a 2 a     1ln a 2      a 2    3ln a 2    0，  设平面QBC的法向量nx,y,z， 解得a2e3，故0a2e3；综上，实数a的取值范围是a  0,2e3  .   B  C  n   3y0  f x  f x  则   C  Q  n   3 x 3 yaz0 ，令x2a，解得：y0，z3，n  2a,0,3； 法三：x 1 x 2  x 2 f x 1 x 1 f x 2   0x 1 x 2   x 1 1  x 2 2   0  2  2   令gx f x x2a lnx ，则只需gx在 单调递增，即gx0恒成立；   MNn 3a 42 x x cosMN,n  M  N   n   3a2  4a29  7 ，解得：a 3或a 3 2 ，故QM的长为 3 或 3 2 gx1 a1 x  2 lnx  x2a x 1 2 lnx m∞ 4 a 18. (17分)解：（1） fx2x2 ，当a1，时， f 11， fx1， x 故切线方程为：y1x1,即yx2； f x  f x  （2）法一：不妨设0x x ，则x f x x f x 0，同除以xx 得 1  2 ， 1 2 2 1 1 2 1 2 x x 1 2 f x alnx a1lnx 所以Gx x2 在 单调递增，所以Gx1 0. x x x2 m∞ 2024-10 高三数月10 第5页共2页即a(lnx1) x2,讨论lnx1的正负； 由题知，当n无限增大时，1 pn趋近于零，n1 pn趋近于零，则EY趋近于 1 . p x2 x2 第一类：lnx10,即xe时，a ,记h(x) 所以当n无限增大时，Y的数学期望趋近于一个常数. lnx1 lnx1 x(2lnx3) 3 3 h(x) ,h(x)在(e,e2)递减，在(e2,)递增， (lnx1)2 3 h(x)h(e2)2e3,即a2e3. 第二类：lnx10,即a e时，0e2恒成立。 x2 第三类：lnx10,即xe时，a ，由上可知h(x)在(0,e)递减， lnx1 x0时，h(x)0,a0. 综上，a[0,2e3] 19. (17分)解：（1）设A “两个粒子通过第一道逻辑门后上旋粒子个数为i个”，i 0,1,2, i B“两个粒子通过第二道逻辑门后上旋粒子个数为2个”， 2 2 1 1 1 1 则PA  PA   ，PAC1    ， 0 2 2 4 1 22 2 1 2 4 P  B∣A  ，P  B∣A  ，P  B∣A  ， 0 9 1 9 2 9 2 1 1 1 2 1 4 1 则PBPAP  B∣A        . i i 4 9 2 9 4 9 4 i0 （2）由题知X 0,1,2， 1 1 1 1 由（1）知PX 2 p2 p1 p 1 p2  ， 4 2 4 4 1 1 1 1 同理可得PX 1 C1p1 p  p21 p2 C1p1 p ， 4 2 2   4 2 2 1 则PX 01PX 1PX 2 ， 4 1 1 1  1 1 1 1 3 故X 的信息熵H  f   f   f  2 log  log  . 4 2 4  4 2 4 2 2 2 2 （3）由题知PY n1 pn1 p，其中n1，2，3，…， 则EY11 p0 p21 p1 pn1 pn1 p， n n 又ip1 pi1  pi1 pi1， i1 i1 n 则i1 pi1 11 p021 p1n1 pn1，① i1 n 1 pi1 pi1 11 p121 p2n1 pn，② i1 n ①②得： pi1 pi1 1 p01 p11 pn1n1 pn i1 11 pn 1 1 pn  n1 pn  n 1 p n ， p p p 2024-10 高三数月10 第6页共2页