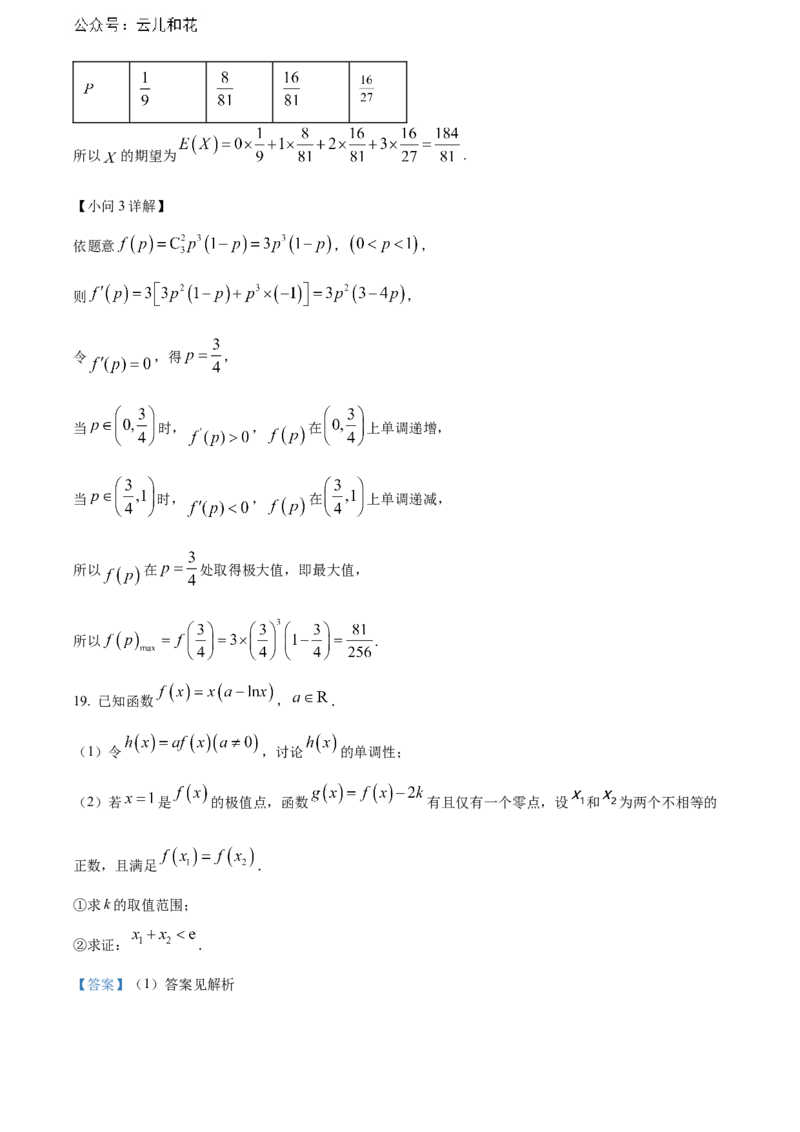文档内容
江门市 2024 年普通高中高二调研测试(二)
数 学
本试卷共6页,19小题,满分150分,测试用时120分钟.
注意事项:
1.答卷前,考生务必将自己的姓名、考生号、考场号和座位号填写在答题卡上.用2B铅笔
将试卷类型(A)填涂在答题卡相应位置上.
2.作答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目选项的答案信息点涂黑;
如需改动,用橡皮擦干净后,再选涂其他答案.答案不能答在试卷上.
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题指定区域内相应
的位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液.
不按以上要求作答无效.
4.考生必须保证答题卡的整洁,考试结束后,将试卷与答题卡一并交回.
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项
是符合题目要求的.
1. 已知函数 ,则 ( )
A. B. C. D.
2. 一个车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了6次试验,收集数据如下表
所示,建立加工时间关于零件数的一元线性回归模型,则回归直线必过点( )
零件数 个 50 60 70 80 90 100
加工时间 min 88 95 102 108 115 122
A. B. C. D.
3. 在等差数列 中, ,若直线l过点 , ,则直线l
的斜率为( )
A. B. C. 2 D. 3
4. 由伦敦著名建筑事务所SteynStudio设计的南非双曲线大教堂惊艳世界,该建筑是数学与建筑完美结合造就的艺术品,若将如图所示的大教堂外形弧线的一段近似看成双曲线 下支的一
部分,离心率为 ,则该双曲线的渐近线方程为( )
A. B. C. D.
5. 某校高二级学生参加期末调研考试的数学成绩X服从正态分布 ,将考试成绩从高到低,按照
16%,34%,34%,16%的比例分为A,B,C,D四个等级.若小明的数学成绩为105分,则属于等级(
)
(附: , ,
)
A. A B. B C. C D. D
6. 已知曲线 在点 处的切线与曲线 有且仅有一个公共点,则实数a
的值是( )
A. B. 0 C. 0或8 D. 8
7. 已知数列 的前n项和为 ,且 ,设 ,则 的前11项和为(
)
A. B. 0 C. 1 D. 2
8. 设事件A,B满足 ,且 , ,则 ( )A. B. C. D.
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题
目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9. 已知椭圆 的左、右焦点分别为 , ,点P是椭圆C上任意一点(非长轴的顶点),
则下列说法正确的是( )
的
A. 椭圆C 焦点坐标为
B. 当 时,椭圆C的离心率为
的
C. 当 时, 周长为6
D. 若椭圆C的离心率为 ,则 的面积的最大值是
10. 在正方体中,下列说法正确的是( )
A. 正方体的8个顶点可以确定28条不同的线段
B. 以正方体的顶点为顶点的直三棱柱有12个
的
C. 以正方体 顶点为顶点的三棱锥有64个
D. 以正方体的顶点为顶点的四棱锥有48个
11. 在正项无穷数列 中,若对任意的 ,都存在 ,使得 ,则称 为
m阶等比数列.在无穷数列 中,若对任意的 ,都存在 ,使得 ,则
称为m阶等差数列,下列说法正确的是( )
A. 若 为1阶等比数列, , ,则 为等比数列且公比2
B. 若 为1阶等差数列, 共有30项,其中奇数项之和为20,偶数项之和为50,则 为等差数
列且公差为2C. 若 为m阶等比数列,则 为m阶等差数列
D. 若 既是3阶等比数列,又是4阶等比数列,则 是等比数列
三、填空题:本题共3小题,每小题5分,共15分.
12. 展开式中 的系数为______.
13. 已知直线 与圆 交于A,B两点,写出满足“ 面积为 ”的m
的一个值____________.
14. 丹麦数学家琴生(Jensen)是19世纪对数学分析做出卓越贡献的巨人,特别是在函数的凹凸性与不等
式方面留下了很多宝贵的成果.设函数 在 上的导函数为 , 在 上的导函数
为 ,若在 上 恒成立,则称函数 在 上为“凸函数”,已知
在 上为“凸函数”,则实数m的取值范围是____________.
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15. 已知数列 满足 , ,数列 是正项等比数列,且 , .
(1)求 , 的通项公式;
(2)从下面①②两个条件中选择一个作为已知条件,求数列 的前 项和 .
① ;② .
16. 为了对高中生进行职业规划教育,让高中生了解信息技术发展的前沿,体验典型人工智能技术的应用
感受和人工智能对学习和生活的影响,激发学生对信息技术未来的追求,某市计划在高一年级推广开设人
工智能研究性学习课程.为调研学生对人工智能的兴趣,随机从某校高一年级学生中抽取了100人进行调
查,其中数据如下表:
有兴趣 没兴趣 合计
男生 48 2 50女生 32 18 50
合计 80 20 100
的
(1)依据小概率值 独立性检验,分析高一学生对人工智能有兴趣与性别是否有关?
(2)以该100名高一学生对人工智能有兴趣的频率作为全市高一学生对人工智能有兴趣的概率,从全市的
高一学生中随机抽取5名学生,记X为这5名学生中对人工智能有兴趣的学生人数,求X的期望与方差.
参考公式: , .
参考数据:
.
005 0.01 0.005 0.001
3.841 6.635 7.879 10.828
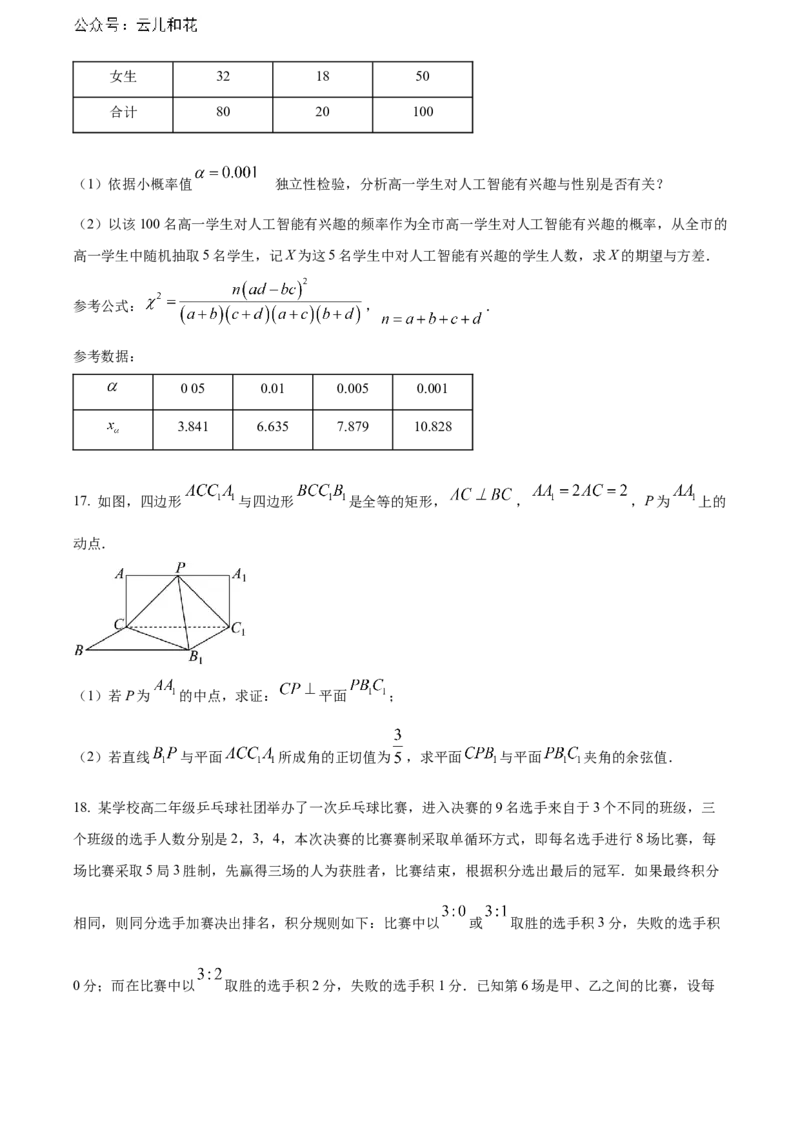
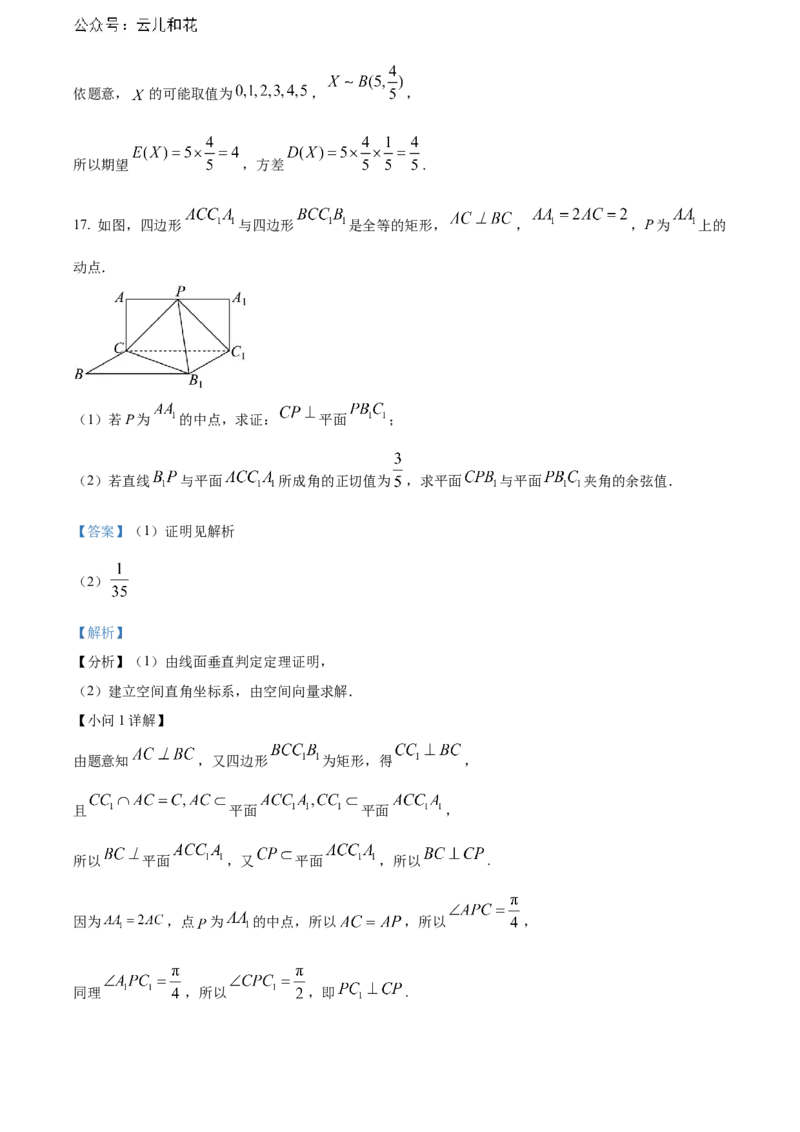
17. 如图,四边形 与四边形 是全等的矩形, , ,P为 上的
动点.
(1)若P为 的中点,求证: 平面 ;
(2)若直线 与平面 所成角的正切值为 ,求平面 与平面 夹角的余弦值.
18. 某学校高二年级乒乓球社团举办了一次乒乓球比赛,进入决赛的9名选手来自于3个不同的班级,三
个班级的选手人数分别是2,3,4,本次决赛的比赛赛制采取单循环方式,即每名选手进行8场比赛,每
场比赛采取5局3胜制,先赢得三场的人为获胜者,比赛结束,根据积分选出最后的冠军.如果最终积分
相同,则同分选手加赛决出排名,积分规则如下:比赛中以 或 取胜的选手积3分,失败的选手积
0分;而在比赛中以 取胜的选手积2分,失败的选手积1分.已知第6场是甲、乙之间的比赛,设每局比赛甲取胜的概率为 .
(1)若进入决赛的9名选手获得冠亚军的概率相等,则比赛结束后冠亚军恰好来自同一个班级的概率是多
少?
(2)在第6场比赛中,当 时,设甲所得积分为 ,求 的分布列及期望
(3)在第6场比赛中,记甲 取胜的概率为 ,求 的最大值.
19. 已知函数 , .
(1)令 ,讨论 的单调性;
(2)若 是 的极值点,函数 有且仅有一个零点,设 和 为两个不相等的
正数,且满足 .
①求k的取值范围;
②求证: .江门市 2024 年普通高中高二调研测试(二)
数学
本试卷共6页,19小题,满分150分,测试用时120分钟.
注意事项:
1.答卷前,考生务必将自己的姓名、考生号、考场号和座位号填写在答题卡上.用2B铅笔
将试卷类型(A)填涂在答题卡相应位置上.
2.作答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目选项的答案信息点涂黑;
如需改动,用橡皮擦干净后,再选涂其他答案.答案不能答在试卷上.
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题指定区域内相应
的位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液.
不按以上要求作答无效.
4.考生必须保证答题卡的整洁,考试结束后,将试卷与答题卡一并交回.
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项
是符合题目要求的.
1. 已知函数 ,则 ( )
A. B. C. D.
【答案】D
【解析】
【分析】求出函数 的导数,再代入求出导数值.
【详解】函数 ,求导得 ,
所以 .
故选:D.
2. 一个车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了6次试验,收集数据如下表
所示,建立加工时间关于零件数的一元线性回归模型,则回归直线必过点( )
零件数 个 50 60 70 80 90 100加工时间 min 88 95 102 108 115 122
A. B. C. D.
【答案】B
【解析】
【分析】求出 , ,根据回归直线方程必过样本中心点 ,即可判断.
【详解】依题意可得 ,
,
所以回归直线必过点 .
故选:B
3. 在等差数列 中, ,若直线l过点 , ,则直线l
的斜率为( )
A. B. C. 2 D. 3
【答案】C
【解析】
【分析】根据给定条件,求出等差数列公差,再利用公差的几何意义求解即得.
【详解】在等差数列 中, ,则公差 ,
所以直线l的斜率为 .
故选:C.
4. 由伦敦著名建筑事务所SteynStudio设计的南非双曲线大教堂惊艳世界,该建筑是数学与建筑完美结合造
就的艺术品,若将如图所示的大教堂外形弧线的一段近似看成双曲线 下支的一部分,离心率为 ,则该双曲线的渐近线方程为( )
A. B. C. D.
【答案】B
【解析】
【分析】求出 的值,可得出双曲线的渐近线方程.
详解】由已知可得 ,
【
因此,该双曲线的渐近线方程为 .
故选:B.
5. 某校高二级学生参加期末调研考试的数学成绩X服从正态分布 ,将考试成绩从高到低,按照
16%,34%,34%,16%的比例分为A,B,C,D四个等级.若小明的数学成绩为105分,则属于等级(
)
(附: , ,
)
A. A B. B C. C D. D
【答案】A
【解析】
【分析】根据正态分布的性质即可求解.【详解】数学测试成绩服从正态分布 ,则 , ,
由于 等级的概率之和为 ,
所以
,而 即
故 为A等级, 为B等级, 为C等级, 为D等级,
故105分为A等级.
故选:A.
6. 已知曲线 在点 处的切线与曲线 有且仅有一个公共点,则实数a
的值是( )
A. B. 0 C. 0或8 D. 8
【答案】D
【解析】
【分析】根据给定条件,求出切线方程,再按 与 分类讨论求解.
【详解】函数 ,求导得 ,则 ,
因此曲线 在点 处的切线方程为 ,即 ,
当 时,曲线 与直线 平行,无公共点,
则 ,曲线 是对称轴为 的抛物线,
因此直线 与曲线 有且仅有一个公共点,当且仅当 只有一个解,即 有相等实根,
于是 ,则 .
故选:D.
7. 已知数列 的前n项和为 ,且 ,设 ,则 的前11项和为(
)
A. B. 0 C. 1 D. 2
【答案】A
【解析】
【分析】根据给定条件,利用分组求和法,结合等比数列前n项和公式计算即得.
【详解】依题意, 的前11项和为 .
故选:A.
8. 设事件A,B满足 ,且 , ,则 ( )
A. B. C. D.
【答案】C
【解析】
【分析】根据条件概率的公式结合已知条件分析判断.
【详解】因为 ,所以 .
因为 , , .
,则 .
所以 .
故选:C.
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9. 已知椭圆 的左、右焦点分别为 , ,点P是椭圆C上任意一点(非长轴的顶点),
则下列说法正确的是( )
A. 椭圆C的焦点坐标为
B. 当 时,椭圆C的离心率为
C. 当 时, 的周长为6
D. 若椭圆C的离心率为 ,则 的面积的最大值是
【答案】AC
【解析】
【分析】求出焦点坐标判断A;求出离心率、焦点三角形周期、面积最大值判断BCD.
【详解】椭圆 的长半轴长 ,短半轴长 ,半焦距 ,
对于A,椭圆C的焦点坐标为 ,A正确;
对于B,当 时, ,离心率 ,B错误;
对于C,当 时, ,则 的周长为 ,C正确;
对于D,椭圆C的离心率为 ,即 ,解得 , ,
设 ,则 的面积 ,D错误.
故选:AC.10. 在正方体中,下列说法正确的是( )
的
A. 正方体 8个顶点可以确定28条不同的线段
B. 以正方体的顶点为顶点的直三棱柱有12个
C. 以正方体的顶点为顶点的三棱锥有64个
D. 以正方体的顶点为顶点的四棱锥有48个
【答案】ABD
【解析】
【分析】利用几何组合计数问题,结合正方体及直三棱柱、三棱锥、四棱锥的构造特征,列式计算即得.
【详解】对于A,每两点确定一条线段,则正方体的8个顶点可确定不同的线段有 条,A正确;
对于B,直三棱柱的两个底面三角形平行并且全等,因此直三棱柱两底面在正方体相对面上,
以正方形的顶点为顶点的三角形有4个,从而正方体的一组相对面对应的直三棱柱有4个,
因此以正方体的顶点为顶点的直三棱柱有 个,B正确;
对于C,正方体顶点任取4个点,共有 种选法,
其中四点共面的共有6个面和6个对角面共12种,因此三棱锥共有 个,C错误;
对于D,由选项C,知正方体四点共面的情况有12种,每一种情况,余下每个点对应1个四棱锥,
因此四棱锥共有 ,D正确.
故选:ABD.
11. 在正项无穷数列 中,若对任意的 ,都存在 ,使得 ,则称 为
m阶等比数列.在无穷数列 中,若对任意的 ,都存在 ,使得 ,则
称为m阶等差数列,下列说法正确的是( )A. 若 为1阶等比数列, , ,则 为等比数列且公比2
B. 若 为1阶等差数列, 共有30项,其中奇数项之和为20,偶数项之和为50,则 为等差数
列且公差为2
C. 若 为m阶等比数列,则 为m阶等差数列
D. 若 既是3阶等比数列,又是4阶等比数列,则 是等比数列
【答案】BCD
【解析】
【分析】对于A,根据题意可得 为正项等比数列,求出首项与公比,再根据等比数列的前 项和公式
即可得解;对于B,根据题意可得 为等差数列,根据题意写出 ,
,两式相减即可得解;对于C,由 为 阶等比数列,可得
,使得 成立,再根据 阶等差数列即可得出结论;对于D,根据
既是3阶等比数列,又是4阶等比数列,可得 与
同时成立,再结合等比数列的定义即可得出结论.
【详解】对于A,因 为为1阶等比数列,所以 ,则 为正项等比数列,
设公比为 ,则 为正数,
由已知得
两式相除得 ,所以 ( 舍去),故A错误.对于B, 因为 为1阶等差数列,则 ,则 为等差数列. 设公差为d.
因为 共有30项,其中奇数项之和为20,偶数项之和为50.
则 , ,两式相减得到 ,
解得 .故B正确.
对于C,因为 为 阶等比数列,
所以 ,使得 成立,
所以 ,
又 ,
所以 ,
即 成立,
所以 为 阶等差数列;故C正确.
对于D,因为 既是3阶等比数列,又是4阶等比数列,
所以 与 同时成立,
所以 与 同时成立,
又 的各项均为正数,所以对任意的 ,
数列 和数列 都是等比数列,
由数列 是等比数列,
得 也成等比数列,a a
设
n+4=q >0(∀n∈N*), n+4=q >0(∀n∈N*),
a 1 a 2
n n+1
a q
所以
n+1= 1>0(∀n∈N*),所以
是等比数列. 故D正确.
a q
n 2
故选:BCD.
【点睛】方法点睛:新定义题型的特点是通过给出一个新的概念来创设全新的问题情境,要求学生在阅读
理解的基础上,依据题目提供的信息,联系所学的知识和方法,实现信息迁移,达到灵活解题的目的,遇
到新定义的问题,应耐心读题,分析新定义,弄清新定义的性质,按新定义的要求运算求解.
三、填空题:本题共3小题,每小题5分,共15分.
12. 展开式中 的系数为______.
【答案】15
【解析】
【分析】写出展开式的通项,即可得解.
【详解】二项式 展开式的通项为 ( 且 ),
所以 展开式中 的系数为 .
故答案为: .
13. 已知直线 与圆 交于A,B两点,写出满足“ 面积为 ”的m
的一个值____________.
【答案】 (答案不唯一)
【解析】
【分析】利用圆的弦长求法,结合面积可得方程求解即可.
【详解】由圆 可知,圆心 ,半径 ,
设圆心 到直线 的距离为 ,
由垂径定理可知 ,
由 面积为 知: ,解得 或 ,则由点到直线的距离公式得: ,
当 时,有 ,解得: ,
当 时,有 ,解得: ,
故答案为: (取 这三个中的任何一个都算对,答案不唯一).
14. 丹麦数学家琴生(Jensen)是19世纪对数学分析做出卓越贡献的巨人,特别是在函数的凹凸性与不等
式方面留下了很多宝贵的成果.设函数 在 上的导函数为 , 在 上的导函数
为 ,若在 上 恒成立,则称函数 在 上为“凸函数”,已知
在 上为“凸函数”,则实数m的取值范围是____________.
【答案】
【解析】
【分析】根据给定的函数,求出 、 ,再利用“凸函数”的定义求解即得.
【详解】函数 ,求导得 , ,
依题意, , 恒成立,
而函数 在 上单调递增, ,则 ,
所以实数m的取值范围是 .故答案为:
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15. 已知数列 满足 , ,数列 是正项等比数列,且 , .
(1)求 , 的通项公式;
(2)从下面①②两个条件中选择一个作为已知条件,求数列 的前 项和 .
① ;② .
【答案】(1) ,
(2)若选① ;若选②
【解析】
【分析】(1)依题意可得 是以 为首项, 为公差的等差数列,即可求出 的通项公式,)根据
等比数列的性质可得出关于 、 的方程组,解出这两个量的值,可求得数列 的公比,进而可求得
数列 的通项公式;
(2)若选①则 利用裂项相消法求得 ;若选②则 ,利用错位
相减法可求得 .
【小问1详解】
因为 , ,即 ,所以 是以 为首项, 为公差的等差数列,
所以 ,
由等比数列的性质可得 ,由题意可得 ,解得 ,所以等比数列 的公比为 ,
所以 .
【小问2详解】
若选①,
,
所以 .
若选②, ,
所以 ,
则 ,
两式相减得
,
因此 ;
16. 为了对高中生进行职业规划教育,让高中生了解信息技术发展的前沿,体验典型人工智能技术的应用
感受和人工智能对学习和生活的影响,激发学生对信息技术未来的追求,某市计划在高一年级推广开设人
工智能研究性学习课程.为调研学生对人工智能的兴趣,随机从某校高一年级学生中抽取了100人进行调
查,其中数据如下表:
有兴趣 没兴趣 合计
男生 48 2 50
女生 32 18 50
合计 80 20 100(1)依据小概率值 的独立性检验,分析高一学生对人工智能有兴趣与性别是否有关?
(2)以该100名高一学生对人工智能有兴趣的频率作为全市高一学生对人工智能有兴趣的概率,从全市的
高一学生中随机抽取5名学生,记X为这5名学生中对人工智能有兴趣的学生人数,求X的期望与方差.
参考公式: , .
参考数据:
0.05 0.01 0.005 0.001
.
3.841 6635 7.879 10.828
【答案】(1)有关; (2)期望4,方差 .
【解析】
【分析】(1)利用给定数表求出 的观测值,再与临界值比对即得.
(2)求出频率,利用二项分布求出期望、方差.
【小问1详解】
零假设 :高一学生对人工智能有兴趣与性别无关,
由给定的数表,得 ,
依据小概率值 的独立性检验,推断 不成立,
即认为高一学生对人工智能有兴趣与性别有关,此推断犯错误的概率不大于0.001.
【
小问2详解】
由数表知,100名高一学生对人工智能有兴趣的频率为 ,
因此全市高一学生对人工智能有兴趣的概率为 ,依题意, 的可能取值为 , ,
所以期望 ,方差 .
17. 如图,四边形 与四边形 是全等的矩形, , ,P为 上的
动点.
(1)若P为 的中点,求证: 平面 ;
(2)若直线 与平面 所成角的正切值为 ,求平面 与平面 夹角的余弦值.
【答案】(1)证明见解析
(2)
【解析】
【分析】(1)由线面垂直判定定理证明,
(2)建立空间直角坐标系,由空间向量求解.
【小问1详解】
由题意知 ,又四边形 为矩形,得 ,
且 平面 平面 ,
所以 平面 ,又 平面 ,所以 .
因为 ,点 为 的中点,所以 ,所以 ,
同理 ,所以 ,即 .又由于 ,所以 ,且 ,
又 平面 平面 ,
所以 平面 ,
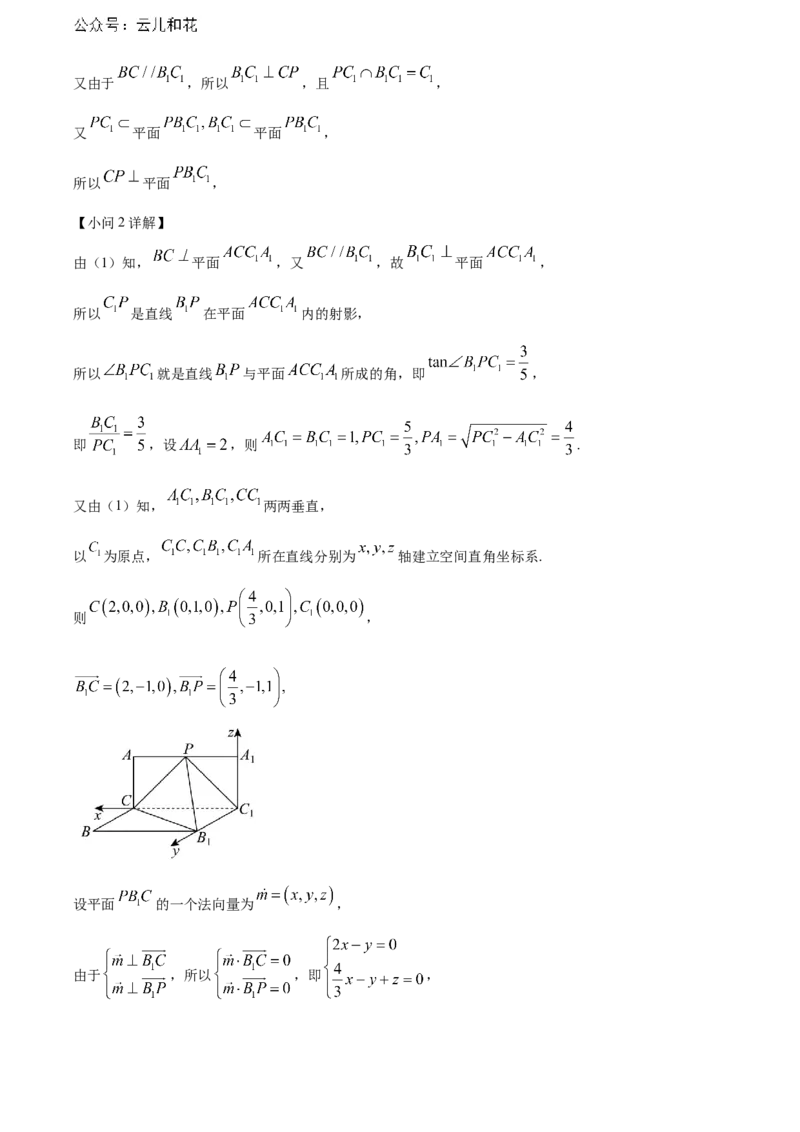
【小问2详解】
由(1)知, 平面 ,又 ,故 平面 ,
所以 是直线 在平面 内的射影,
所以 就是直线 与平面 所成的角,即 ,
即 ,设 ,则 .
又由(1)知, 两两垂直,
以 为原点, 所在直线分别为 轴建立空间直角坐标系.
则 ,
设平面 的一个法向量为 ,
由于 ,所以 ,即 ,令 ,则 ,即 ,
设平面 的一个法向量为 ,
,
由于 ,所以 ,即 ,
令 ,则 ,即 ,
设平面 与平面 的夹角为 ,可知 为锐角,
所以 .
故平面 与平面 夹角的余弦值为 .
18. 某学校高二年级乒乓球社团举办了一次乒乓球比赛,进入决赛的9名选手来自于3个不同的班级,三
个班级的选手人数分别是2,3,4,本次决赛的比赛赛制采取单循环方式,即每名选手进行8场比赛,每
场比赛采取5局3胜制,先赢得三场的人为获胜者,比赛结束,根据积分选出最后的冠军.如果最终积分
相同,则同分选手加赛决出排名,积分规则如下:比赛中以 或 取胜的选手积3分,失败的选手积
0分;而在比赛中以 取胜的选手积2分,失败的选手积1分.已知第6场是甲、乙之间的比赛,设每
局比赛甲取胜的概率为 .
(1)若进入决赛的9名选手获得冠亚军的概率相等,则比赛结束后冠亚军恰好来自同一个班级的概率是多
少?
(2)在第6场比赛中,当 时,设甲所得积分为 ,求 的分布列及期望
(3)在第6场比赛中,记甲 取胜的概率为 ,求 的最大值.【答案】(1)
(2)分布列见解析,
(3)
【解析】
【分析】(1)根据古典概型的概率公式计算可得;
(2)依题意 的可能取值为 ,求出所对应的概率,即可求出分布列与数学期望;
(3)依题意 ,利用导数说明函数的单调性,即可求出函数的最大值.
【小问1详解】
记比赛结束后冠亚军恰好来自同一个班级为事件 ,
则 ;
【小问2详解】
依题意 的可能取值为 ,
所以 ,
,
,
.
所以 的分布列为所以 的期望为 .
【小问3详解】
依题意 , ,
则 ,
令 ,得 ,
当 时, , 在 上单调递增,
当 时, , 在 上单调递减,
所以 在 处取得极大值,即最大值,
所以 .
19. 已知函数 , .
(1)令 ,讨论 的单调性;
(2)若 是 的极值点,函数 有且仅有一个零点,设 和 为两个不相等的
正数,且满足 .
①求k的取值范围;
②求证: .
【答案】(1)答案见解析(2) 或 ;证明见解析
【解析】
【分析】(1)先求导函数,再分类讨论导函数正负得出函数的单调区间;
(2)①先根据极值点求出 ,再把有一个零点转化结合函数图形求出参数范围即可;②构造函数再应
用导函数确定函数单调性证明不等式.
【小问1详解】
ℎ(x)=af (x)=ax(a−lnx)(x>0),
,
函数 为减函数,
令 ,则 ,
当 时,令 ,得 ,令 ,得 ,
所以函数 的单调增区间为 ,减区间为 ,
当 时,令 ,得 ,令 ,得 ,
所以函数 的单调减区间为 ,增区间为 ,
综上所述,当 时,函数 的单调增区间为 ,减区间为 ;
当 时,函数 的单调减区间为 ,增区间为 ;
【小问2详解】
① ,
因为 是 的极值点,所以 ,解得 ,
经检验符合题意,
则 , ,
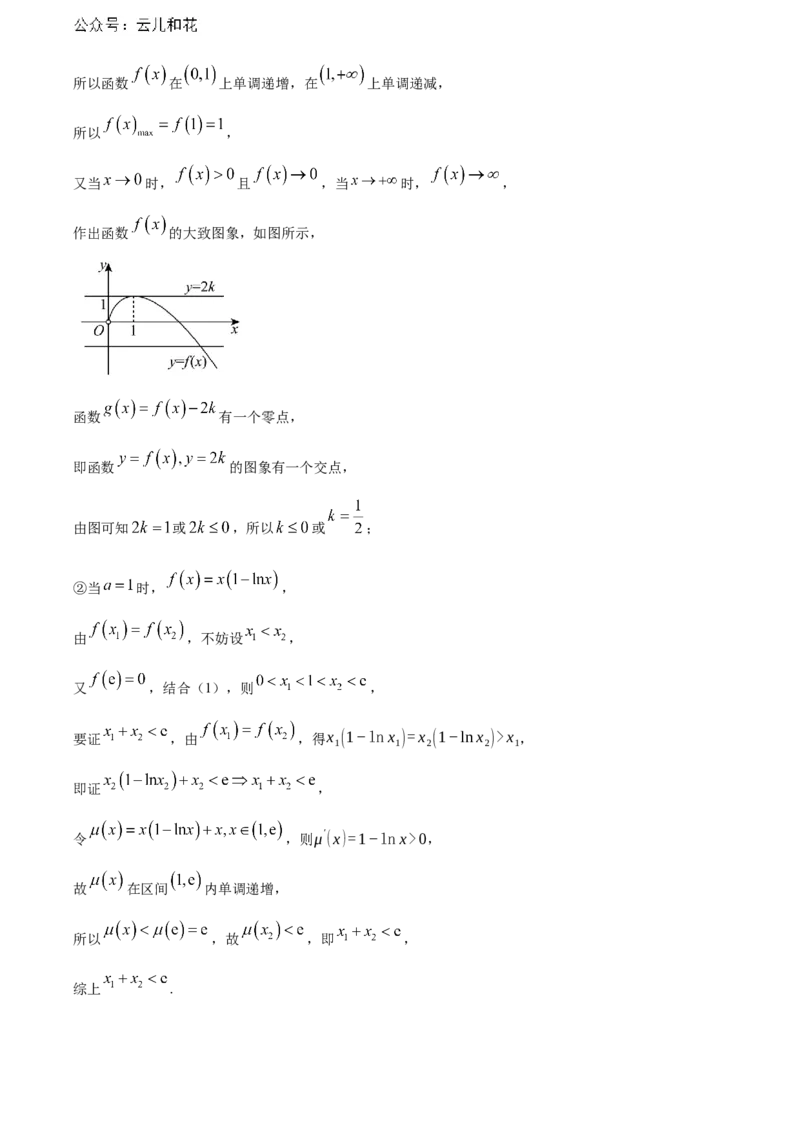
当 时, ,当 时, ,所以函数 在 上单调递增,在 上单调递减,
所以 ,
又当 时, 且 ,当 时, ,
作出函数 的大致图象,如图所示,
函数 有一个零点,
即函数 的图象有一个交点,
由图可知 或 ,所以 或 ;
②当 时, ,
由 ,不妨设 ,
又 ,结合(1),则 ,
要证 ,由 ,得x (1−lnx )=x (1−lnx )>x ,
1 1 2 2 1
即证 ,
令 ,则μ′(x)=1−lnx>0,
故 在区间 内单调递增,
所以 ,故 ,即 ,
综上 .【点睛】方法点睛:利用导数解决函数零点问题构造新函数法,将问题转化为研究两函数图象的交点问题;