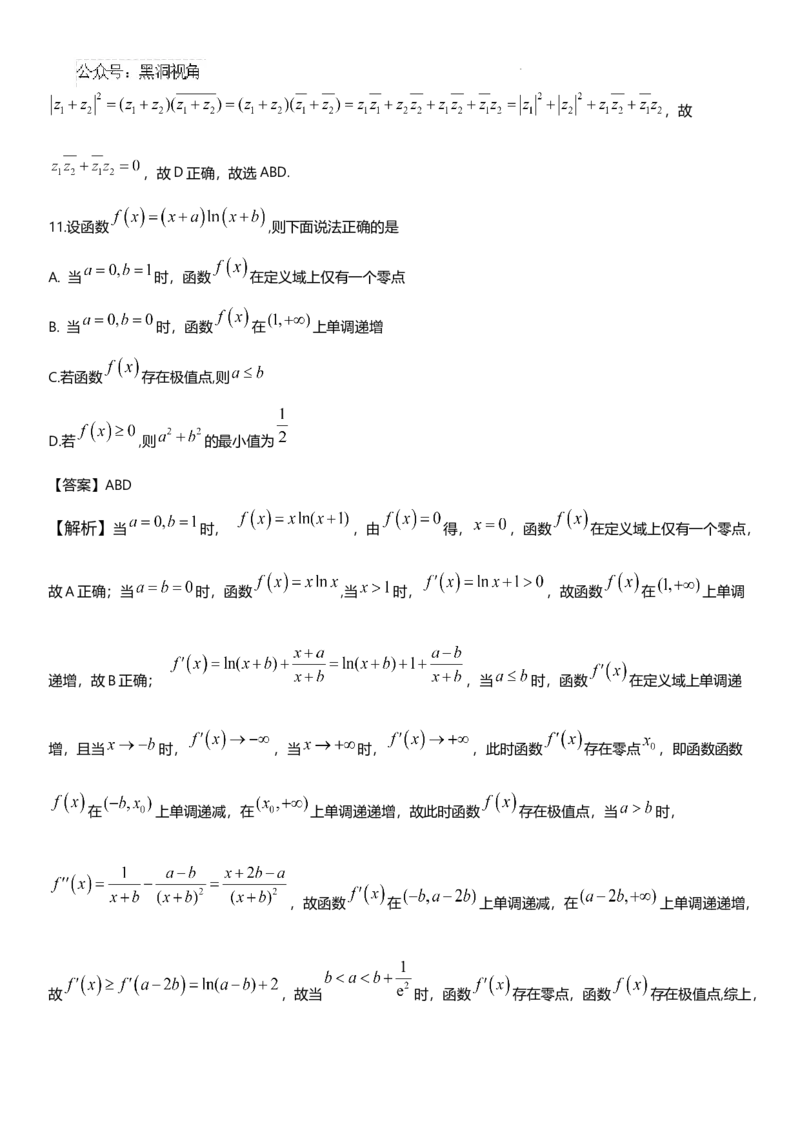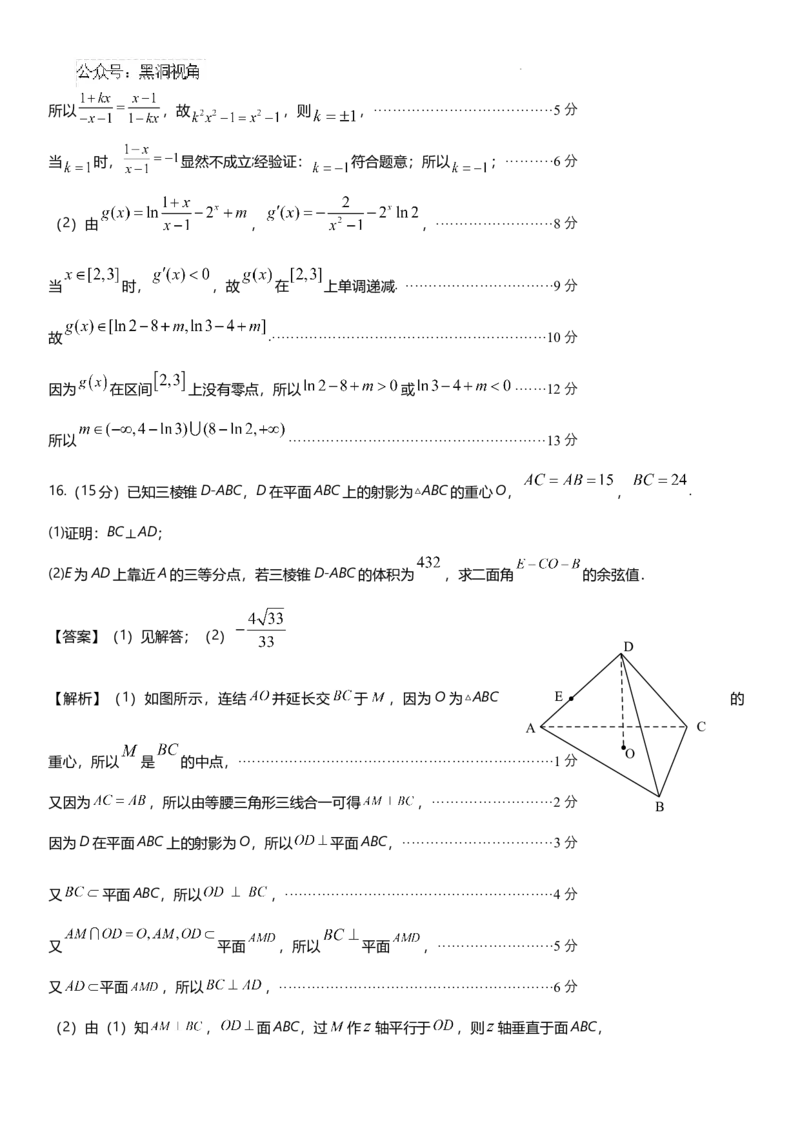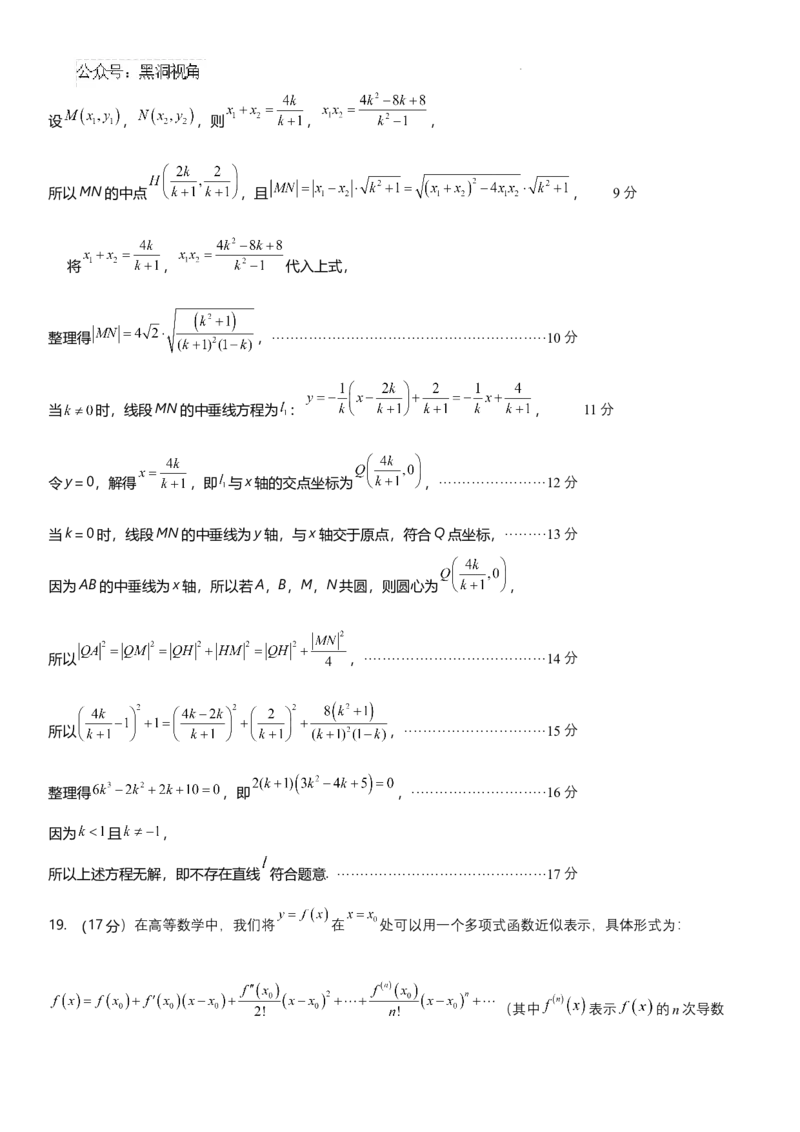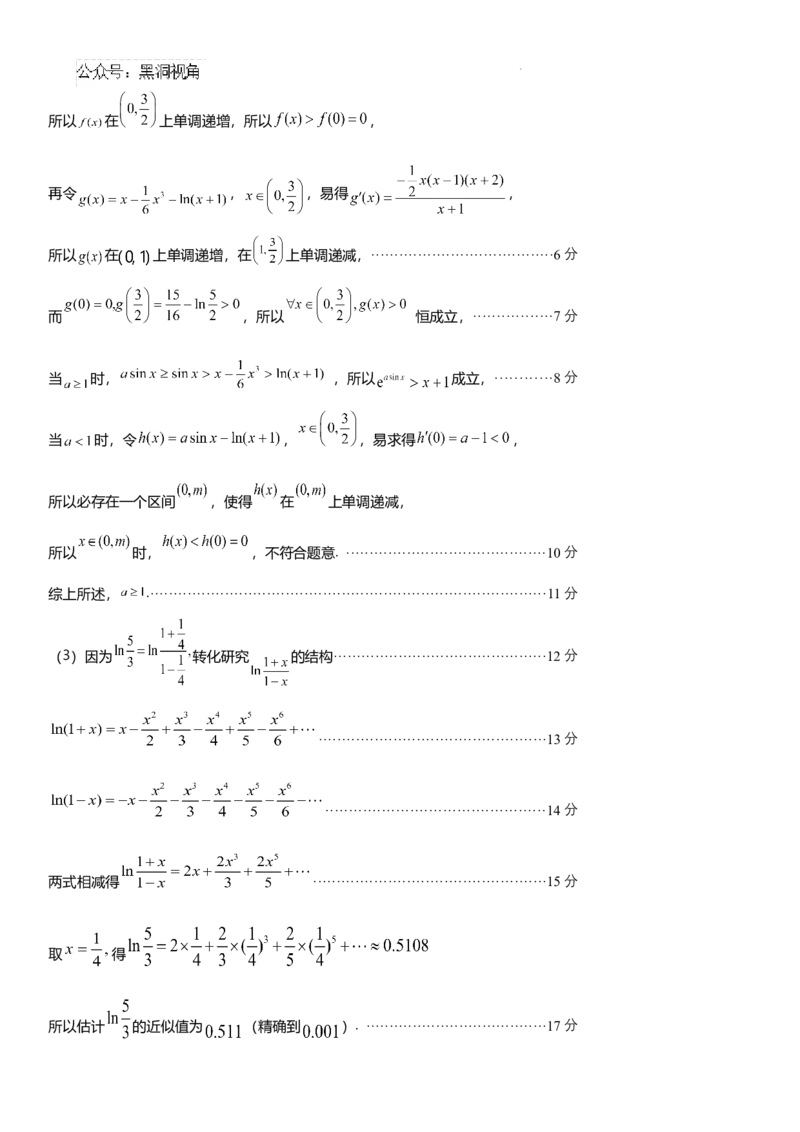文档内容
成都石室中学 2024~2025 学年度上期高 2025 届十月月考
数学参考答案
一、 选择题:本大题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是
符合题目要求的,请把正确的选项填涂在答题卡相应位置.
1. 已知集合 , ,则
A. B. C. D.
【答案】B
【解析】 ,故 ,故选B.
2. 2024年巴黎奥运会中国代表队获得金牌榜第一,奖牌榜第二的优异成绩.首金是中国组合黄雨婷和盛李豪在10米
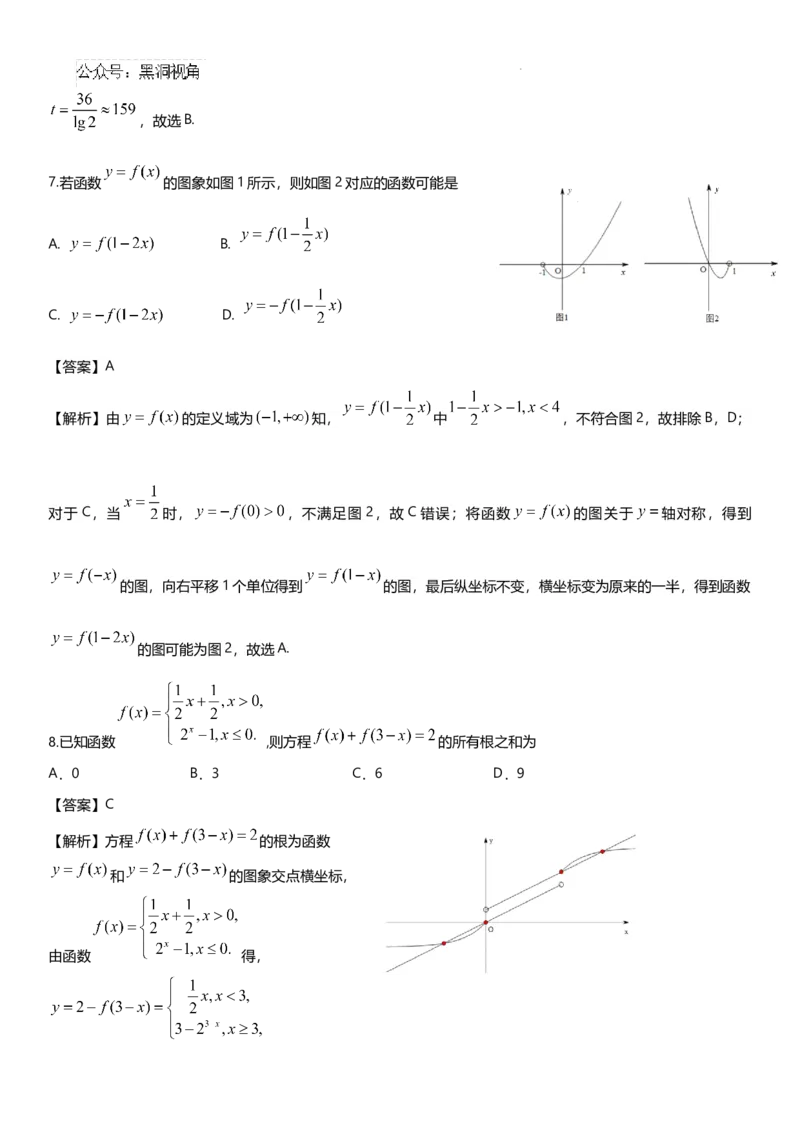
气步枪混合团体赛中获得,两人在决赛中14次射击环数如右图,则
A.盛李豪的平均射击环数超过10.6
B.黄雨婷射击环数的第80百分位数为10.65
射击成绩图
C.盛李豪射击环数的标准差小于黄雨婷射击环数的标准差
10.8
D.黄雨婷射击环数的极差小于盛李豪射击环数的极差 10.6
10.4
【答案】C
10.2
【解析】盛李豪的射击环数只有两次是 10.8环,5次10.6 10 环 ,
9.8
其余都是 10.6 环以下,所以盛李豪平均射击环数低于 9.6
1 2 3 4 5 6 7 8 9 10 11 12 13 14
10.6,故A错误;由于 ,故第80百分位数是从 小
盛李豪 黄雨婷
到大排列的第12个数10.7,故B错误;由于黄雨婷的射击 环
数更分散,故标准差更大,故C正确;黄雨婷射击环数的极差为 10.8-9.7=1.1,盛李豪的射击环数极差为10.8-
10.3=0.5,故D错误.故选C.
3.已知 , , ,则 , , 的大小关系为
A. B. C. D.
【答案】A
【解析】由于 在 单调递减,故 ,又因为 ,所以 ,故选A.
学科网(北京)股份有限公司4.已知实数 , , 满足 ,且 ,则下列说法正确的是
A. B. C. D.
【答案】C
【解析】由题, ,取 ,则 ,故 A错误; ,故 B错误;
,故D错误;因为 ,所以 ,即 ,故C正确.故
选C.
5. “函数 的值域为R”的一个充分不必要条件是
A. B. C. D.
【答案】D
【解析】因为函数 的值域为R,所以在方程 中, ,即 ,
解得 或 ,从而 是“函数 的值域为R”的充分不必要条件.故选D.
6. 核燃料是重要的能量来源之一,在使用核燃料时,为了冷却熔化的核燃料,可以不断向反应堆注入水,但会产
生大量放射性核元素污染的冷却水,称为核废水.核废水中含有一种放射性同位素氚,它有可能用辐射损伤细胞和
组织,影响生物的繁殖和生态平衡。已知氚的半衰期约为 12年,则氚含量变成初始量的 大约需要经过
( )年.( )
A. 155 B.159 C. 162 D. 166
【答案】B
【解析】设氚含量变成初始量的 大约需要经过 t 年,则 , ,即
学科网(北京)股份有限公司,故选B.
7.若函数 的图象如图1所示,则如图2对应的函数可能是
A. B.
C. D.
【答案】A
【解析】由 的定义域为 知, 中 ,不符合图2,故排除B,D;
对于C,当 时, ,不满足图 2,故C错误;将函数 的图关于 轴对称,得到
的图,向右平移1个单位得到 的图,最后纵坐标不变,横坐标变为原来的一半,得到函数
的图可能为图2,故选A.
8.已知函数 ,则方程 的所有根之和为
A.0 B.3 C.6 D.9
【答案】C
【解析】方程 的根为函数
和 的图象交点横坐标,
由函数 得,
学科网(北京)股份有限公司如下图所示,两函数图象共有4个交点,且由于两个函数图象关于点 中心对称,故
方程 的所有根之和为6,故选C.
二、选择题:本大题共3小题,每小题6分,共18分。在每小题给出的选项中,有多项符合题目要求。全部选对的得6
分, 部分选对的得部分分,有选错的得0分,。
9.已知函数 的定义域为 , ,则
A. B.
C.f (x)是奇函数 D.f (x)在 上单调递增
【答案】 AC
【解析】由 知,当 时, ,即 ,故 A 正确;若
,则 满足条件 ,但 ,且f (x)是在 上单调递减,故B,D
错误;当 时, ,即 ,故C正确,故选AC.
10.已知复数 的共轭复数分别为 ,则下列命题为真命题的是
A. B.
C.若 ,则 D.若 ,则
【答案】ABD
【解析】设 且 ,则 ,
,
所以 ,所以 ,故A正确;
, ,故B正确;当
时,满足 ,但不能得出 ,故C错误;
学科网(北京)股份有限公司,故
,故D正确,故选ABD.
11.设函数 ,则下面说法正确的是
A. 当 时,函数 在定义域上仅有一个零点
B. 当 时,函数 在 上单调递增
C.若函数 存在极值点,则
D.若 ,则 的最小值为
【答案】ABD
【解析】当 时, ,由 得, ,函数 在定义域上仅有一个零点,
故A正确;当 时,函数 ,当 时, ,故函数 在 上单调
递增,故B正确; ,当 时,函数 在定义域上单调递
增,且当 时, ,当 时, ,此时函数 存在零点 ,即函数函数
在 上单调递减,在 上单调递递增,故此时函数 存在极值点,当 时,
,故函数 在 上单调递减,在 上单调递递增,
故 ,故当 时,函数 存在零点,函数 存在极值点,综上,
学科网(北京)股份有限公司当函数 存在极值点时, 或 ,故C错误;对于D, 恒成立,当
时, 或 ,当且仅当两个零点重合时, 即 ,函数 在 上单调递
减,在 上单调递增,满足 , 则 ,当 时取“=”,故D
正确,故选ABD.
三、填空题:本题共3小题,每小题5分,共15分。
12.若函数 在 上单调,则实数 的取值范围为_____.
【答案】 或
【解析】函数 的对称轴为 ,故当 或 时,函数 在 上单调,
即 或 ,故答案为 或 .
13.若 是定义在 R 上的奇函数, , ,则
________.
【答案】2
【解析】因为 是定义在R上的奇函数,故 ,又因为 ,
所以 ,故 ,所以, ,即 的周期为4,
由于 为定义在 R 上的奇函数,故 , , ,故
,
故答案为2.
14. 若过点 作曲线 的切线有且仅有两条,则 的取值范围是 .
学科网(北京)股份有限公司【答案】
【解析】设切点为 , ,故切线方程为 ,将 代入切
线方程得 ,
令 ,则
,
故 的单调减区间 ,增区间是 .当 时, ,当 时,
, ,当 与 有且仅有两个交点时, ,故答案为
.
四、解答题:本题共5小题,共77分。解答应写出文字说明、证明过程或演算步骤。
15.(13分)已知函数 为奇函数.
(1)求实数 的值;
(2)若函数 ,且 在区间 上没有零点,求实数 的取值范围.
【答案】(1) ;(2)
【解析】(1)因为 是奇函数,所以 ,·············1分
即 ,···························································3分
学科网(北京)股份有限公司所以 ,故 ,则 ,······································5分
当 时, 显然不成立;经验证: 符合题意;所以 ;··········6分
(2)由 , ,·························8分
当 时, ,故 在 上单调递减. ································9分
故 .···························································10分
因为 在区间 上没有零点,所以 或 ·······12分
所以 ·······················································13分
16.(15分)已知三棱锥D-ABC,D在平面ABC上的射影为△ABC的重心O, , .
(1)证明:BC⊥AD;
(2)E为AD上靠近A的三等分点,若三棱锥D-ABC的体积为 ,求二面角 的余弦值.
【答案】(1)见解答;(2)
D
【解析】(1)如图所示,连结 并延长交 于 ,因为O为△ABC E 的
A C
O
重心,所以 是 的中点,····································································1分
又因为 ,所以由等腰三角形三线合一可得 ,··························2分 B
因为D在平面ABC上的射影为O,所以 平面ABC,································3分
又 平面ABC,所以 ,··························································4分
又 平面 ,所以 平面 ,·························5分
又 平面 ,所以 ,···························································6分
(2)由(1)知 , 面ABC,过 作 轴平行于 ,则 轴垂直于面ABC,
学科网(北京)股份有限公司如图以 为 轴, 轴,建立空间直角坐标系,·····································7分
在 中, , 由(1)知, , 故 z
D
, E
x
C
A
O
, 8分 M
B
y
所 以 三 棱 锥 A-BCD 的 体 积 为 , 则
因为 为△ABC的重心,故 ,··············································9分
则 ,
因为E为AD上靠近A的三等分点,所以 ,
故 ·································································10分
设 为平面 的一个法向量,则 ,
取 ,则 ,故 ,········································12分
易得 是平面 的一个法向量,·················································13分
设二面角 的平面角为 ,则 为钝角,
所以 ,
学科网(北京)股份有限公司所以二面角 的余弦值为 .·················································15分
17. (15分)某小区有3000名居民,想通过验血的方法筛选乙肝病毒携带者,假设携带病毒的人占 .为减轻工
作量,随机地按 人一组分组,然后将各组 个人的血样混合在一起化验.若混合血样呈阴性,说明这 个人全部
阴性;若混合血样呈阳性,说明其中至少有一人的血样呈阳性,就需要对每个人再分别化验一次。
(1)若 试估算该小区化验的总次数;
(2)若 ,且每人单独化验一次花费10元, 人混合化验一次花费 元,求当 为何值时,每个居
民化验的平均费用最少.
注:假设每位居民的化验结果呈阴性还是阳性相互独立.当 时, .
【答案】(1)270;(2)10
【解析】(1)设每组需要检验的次数为X,若混合血样为阴性,则X=1,若混合血样呈阳性,则X=21,1分
所以 , ,·······················3分
所以
·······································································5分
一共有 组,故估计该小区化验的总次数是 .·········7分
(2)设每组n人总费用为Y元,若混合血样呈阴性,则Y=n+9;若混合血样呈阳性,则Y=11n+9, 8分
故 , ····················10分
···········12分
每位居民的化验费用为
= 元······14分
学科网(北京)股份有限公司当且仅当 ,即 时取等号,故n=10时,每个居民化验的平均费用最少.15分
18. (17分)在平面直角坐标系 中,已知 , ,动点P满足 ,且 .设动点P
形成的轨迹为曲线C.
(1)求曲线C的方程;
(2)过点 的直线l与曲线C交于M,N两点,试判断是否存在直线 ,使得A,B,M,N四点共圆.若存在,
求出直线 的方程;若不存在,说明理由.
【答案】(1) ;(2)不存在
【解析】(1)设 ,则 , , ,················1分
因为 ,所以 ,·················2分
所以 , ,所以 , ,···································3分
又因为 ,整理得 ,···········································4分
所以曲线C的方程为 ;·······························································5分
(2)易知当 的斜率不存在时,直线l与曲线C没有两个交点,所以直线l的斜率存在, 6分
设l: ,将直线l与曲线C联立,得 ,
消去y,整理得 ,·································7分
因为 且 ,
所以 且 ,·················································································8分
学科网(北京)股份有限公司设 , ,则 , ,
所以MN的中点 ,且 , 9分
将 , 代入上式,
整理得 ,···························································10分
当 时,线段MN的中垂线方程为 : , 11分
令y=0,解得 ,即 与x轴的交点坐标为 ,·······················12分
当k=0时,线段MN的中垂线为y轴,与x轴交于原点,符合Q点坐标,·········13分
因为AB的中垂线为x轴,所以若A,B,M,N共圆,则圆心为 ,
所以 ,·······································14分
所以 ,······························15分
整理得 ,即 ,·····························16分
因为 且 ,
所以上述方程无解,即不存在直线 符合题意. ·············································17分
19. (17分)在高等数学中,我们将 在 处可以用一个多项式函数近似表示,具体形式为:
(其中 表示 的n次导数
学科网(北京)股份有限公司),以上公式我们称为函数 在 处的泰勒展开式.当 时泰勒展开式也称为麦克劳林公式.
比如 在 处的麦克劳林公式为: ,
由此当 时,可以非常容易得到不等式
请利用上述公式和所学知识完成下列问题:
(1)写出 在 处的泰勒展开式.
(2)若 , 恒成立,求a的范围;(参考数据 )
(3)估计 的近似值(精确到 )
【答案】(1) ;(2) ;(3)
【解析】(1) 在 处的泰勒展开式为:
,············································2分
(2)因为
由 在 处的泰勒展开式,先证 ,
令 ,······················3分
,易知 ,所以 在 上单调递增,
所以 ,所以 在 上单调递增,所以 ,·····4分
学科网(北京)股份有限公司所以 在 上单调递增,所以 ,
再令 , ,易得 ,
所以 在 上单调递增,在 上单调递减,·······································6分
而 ,所以 恒成立,·················7分
当 时, ,所以 成立,············8分
当 时,令 , ,易求得 ,
所以必存在一个区间 ,使得 在 上单调递减,
所以 时, ,不符合题意. ···········································10分
综上所述, .·····················································································11分
(3)因为 转化研究 的结构··············································12分
·················································13分
···············································14分
两式相减得 ··················································15分
取 得
所以估计 的近似值为 (精确到 ). ·······································17分
学科网(北京)股份有限公司