湖北省名校联考2023-2024学年高三上学期11月期中考试数学试题答案(1)_2023年11月_0211月合集_2024届湖北省名校联考高三上学期11月期中考试

绝密★启用前（新高考卷） 数学试卷参考答案 1.【答案】B 1 【解析】z  2  2i，故z  2i，z 在复平面内对应的点为(2,1)，在第二象限. i 2．【答案】A 【解析】因为x∁ R N ，所以xN ，又因为xM ，所以xM  N ，故MN. 3.【答案】C 【解析】由题设可知 b  2，ab0，故(ab)(a2b) a 22b 2 0， a 2. 4.【答案】D 【解析】由S  S  20，可知a 0，5a S 20，a 4，2a  a a  a 8. 4 5 5 3 5 3 3 1 5 1 5.【答案】C   7 2 【解析】极大值点为x  k ，其中kZ，则x  , 满足；极小值点为x  k ， 6 6 6 3 2 其中kZ，则x  满足，故在区间(0,5)有2个极大值点和1个极小值点． 3 6.【答案】A 【解析】方法1：因为AB 与FE共线，故AB∥FE .过D作x轴的垂线，垂足为H ，设 1 1 O为坐标原点，因为D为线段 AB 的中点，故H 为线段OA 的中点，且 1 1 A F A E OA 2 ac 2 c 1 2  2  2  ，设c 为C 的半焦距，则  ，所以C 的离心率e  ． AA A D HA 3 2a 3 a 3 1 2 2 2 a b b b 方法2：设A (a,0)，A (a,0)，B(0,b)，则D( , )，直线A D的方程为：y   x ， 1 2 2 2 2 3a 3 b b 故E(0, )．设c为C 的半焦距，则FE (c, )，AB (a,b)，若AB 与FE共线，则 1 1 3 3 ab c 1 cb 0，所以C 的离心率e  ． 3 a 3 7.【答案】A 【解析】如图，设BD，CD的中点分别为O ，O ，则OO ∥CB， 1 2 1 2 因为平面CBD平面ABD，且CBBD，所以CB平面ABD， 故OO 平面ABD，由几何关系可知O CO AO BO D， 1 2 2 2 2 2 故 O 为 三 棱 锥 C ABD 的 外 接 球 球 心 ， 易 知 2 数学试题参考答案（新高考卷） 第1页（共12页） {#{QQABZYSQogAAAABAAAgCUwUgCgEQkAGCCIoGBAAMIAABwQNABAA=}#}1 1 1 AB2  AD2 13 OO  CB  CB 1 ， O B  BD   ， 所 以 球 半 径 1 2 1 2 2 2 2 2 17 R O B  OO2 O B2  ，故球的表面积为4R2 17. 2 1 2 1 2 8.【答案】D      【解析】方法1：因为，， (0, )，由  可知 ；由2sin sin 2 2 2 4 2  1   可知sinsincos sin，所以； sinsin  sin( )cos， 2 2 2 2 sin2 1cos2 则sin21 1 cos0.1，所以(cos2)2 1.4， 4 4 2  所以cos2 1.40.8 ， ，所以. 2 4    方法2：因为  ，2sin sin，所以2cossin．因为sin2cos0.1， 2 2 2 sin2 1 1cos2 1 10 35 所以 cos 1，即 cos 1，解得cos ， 4 10 4 10 5 sin 20 35110  cos  ．将2sin sin两边平方后，可化简得： 2 10 2 162 35 13 cos12cos2 ，所以coscos，cos2cos2 35 0，即 5 2  coscos．由于，， (0, )，所以． 2 9.【答案】BC 【解析】V 的值与n的大小没有必然联系，无法确定V V 值的变化，故A 错误；若 c c fc v v v ，则去掉v 后V 的值变大，因此TPI的值变小，故B正确；若当v V ， 1 2 n 1 c 1 c 则去掉v 后得到的TPI 的值不变，故C正确；若v V ，无法判断样本v ,v ,,v 的方 1 1 c 2 3 n 差与样本v ,v ,,v 的方差之间的大小关系，故D错误. 1 2 n 10.【答案】ABD 【解析】因为点B ，C ，E ，F 不共面，所以两条直线为异面直线，故A正确；过四点的 1 两条直线共有3种情况，其中仅当一条直线过B ，F ，另一条直线过C ，E 时，这两条直 1 数学试题参考答案（新高考卷） 第2页（共12页） {#{QQABZYSQogAAAABAAAgCUwUgCgEQkAGCCIoGBAAMIAABwQNABAA=}#}1 线相互垂直，故相互垂直的概率为 ，故B正确；两条直线互相平行的概率为0，而两条直 3 线互相垂直的概率小于1，故两条直线互相平行与互相垂直不是对立事件，C错误；BC， 1 BE，BF中，只有BC与AC 垂直，且当BC  AC 时，EF 与AC 不垂直，故D正确. 1 1 1 1 1 1 1 11.【答案】ACD 【解析】由题设可知b(54a)  a1，且a(14b) 15b ，因为a ，b为正数，所以 1 5b 1 a10，14b 0，即a 1，0b  ，故A正确，B错误；由题设可知1 4b 4 a a 1 b b b b 1 b 1 ≥2 4b 4 ，则5( )24 1≤0，故0 ≤ ，所以 ≤ ，即a≥25b， a a a a a 5 a 25 1 5 故 C 正确；由题设可知 a b 0 ，其中 1 40，故 1 a( 1 4) 9 5 ≥ 1 b b b 1 4 4 b b 1 9 a5b1 a5b1 2 ( 4) 511，即1ab≥11b，由题设可知ab ，所以1 ≥ b 1 4 4 4 b 11b，即a3≥49b，故D正确. 12.【答案】ABD 【解析】设直线FA ，FB 在C 上的反射线分别为 AM ，BN ，则 AM ∥BN ∥x轴.设G ， H 分别为线段PA ，PB 延长线上的点，结合光的反射定律可知PAF GAM ， PBF HBN ，由几何关系可知APB ，设AB交x轴于M ，则 AFB AFM BFM  22，所以AFB  2APB ，故A正确； p 设 A(x ,y )，其中 y  0，C 在A处的切线的斜率为k  ，故C 在A处的切线方程 1 1 1 1 2x 1 p 2px 2px 为 y  (x x ) 2px ，令x  0 ，则 y 1 ，即D(0, 1)，故直线DF 的 2x 1 1 2 2 1 2x 斜率为k   1 ，所以k k  1，故 AD  DF ，同理可知BE  EF .因为四边形 2 1 2 p PDFE 的内角和为360，所以APBDFE180，故B正确； p 设B(x ,y )，其中 y  0，同上可知C 在B处的切线方程为 y   (x x ) 2px ， 2 2 2 1 2 2x 2 数学试题参考答案（新高考卷） 第3页（共12页） {#{QQABZYSQogAAAABAAAgCUwUgCgEQkAGCCIoGBAAMIAABwQNABAA=}#}2px  2px p(x x ) p2 求得P( x x , 1 2 )，所以 PF 2  x x  1 2  ，且由抛物线的几何 1 2 2 1 2 2 4 p p 性质可知 AF  x  ，BF  x  ，所以 PF 2  AF  BF ，2PF  2 AF  BF 1 2 2 2 ≤ AF  BF ，当且仅当 AF  BF 时等号成，故C错误； 2 2 2DF 2EF 设O 为坐标原点，易知△AFD ∽△DFO ，则 AF  ，同理 BF  ，所以 p p 2 AF DF  ，故D正确. BF EF 2 13.【答案】135 【解析】常数项为C2(3)2 135. 6   x24x,x[0,4)， 14.【答案】 f(x)  x24x,x(4,0)． 【解析】以点(2,0) 为圆心，半径为2的圆在 x轴上方的部分的方程为 y  x2 4x （0x4），因为 f(x)是奇函数，则 f(0)0，且当x(4,0)时，y x2 4x，所   x2 4x,x[0,4)， 以 f(x)的解析式为 f(x)  x2 4x,x(4,0)． 5 15.【答案】5:6（或写成 ） 6 【解析】如图，连接 AC ，因为G 为CD的中点，且 EF:AB3:4，则四边形DEFG 与△CFG 的面积比为 5:2，所以V :V 5:2，又易知△ACG 与△ABC 1 ACFG 的 面 积 比 为 1:2 ， 所 以 V :V V :V 1:2 2:4 ， 所 以 ACFG FABC FACG FABC V :V V :(V V )5:(24)5:6. 1 2 1 ACFG FABC  1  1 1 1 16.【答案】(0，e 2)(e 2， 1)（或写成(0, )( ,1)） e e 1 【解析】方法1：由 f(x)a2ax x 得 f(x)(2alna)a2ax 1， 2a f(x)(2alna)2a2ax 0 (a0)， f(x)是单调递增函数．根据题意 f(x)0有解，所以 数学试题参考答案（新高考卷） 第4页（共12页） {#{QQABZYSQogAAAABAAAgCUwUgCgEQkAGCCIoGBAAMIAABwQNABAA=}#}ln(2alna) 0a1．由 f(x )0得x  ．当x x 时， f(x)0， f(x)单调递减； 0 0 2alna 0 1lnaln(2alna) 当x x 时， f(x)0， f(x)单调递增，故 f(x)  f(x ) ． 0 min 0 2alna 1 1 设g(a)1lnaln(2alna)(0a1)，则g(a) ( 2) ．由g(a )0得a  a lna 0 0  1  1  1 e 2，当xe 2时，g(a)0，g(a)单调递增；当xe 2时，g(a)0，g(a)单调递减．所 1  以g(a)  g(e 2)0．再结合当x时，f(x)，当x时，f(x)知 max 1 1   a的取值范围为(0，e 2)(e 2， 1)． 1 1 ln ax 方法2：令 f(x)a2ax x 1 0，则 a  lna 2 ，设g(x) lnx ，则g(x) 12lnx ， 2a 1 a2ax1 x2 x3 a2 1 1 当0 xe2时，g(x)0，g(x)单调递增，当xe2时，g(x)0，g(x)单调递减，又因 为当x1时，g(x)0，且当x时，g(x)0，所以若 f(x)有两个零点，只需满足 1 1 1 1 1 1   1 e2或 e2 ，所以a的取值范围是(0,e 2)(e 2,1)． a a 17.（10分） 【解析】（1）方法1：由bsinA 3acosB 3c及正弦定理可得： sinBsin A 3sin AcosB 3sinC  3sin(AB)， ……2分 所以sinBsin A 3sin AcosB  3sin AcosB 3cosAsinB， 故sinBsin A 3cosAsinB， ……3分 因为sinB0，故sin A 3cos A0， 所以tanA 3 ， ……4分  所以 A  . ……5分 3 方法2：由bsinA 3acosB 3c及余弦定理可得： 3a(a2c2b2) bsinA  3c， ……2分 2ac 3(b2 c2 a2) 所以sin A  3cosA0， 2bc 所以tanA 3 ， ……4分 数学试题参考答案（新高考卷） 第5页（共12页） {#{QQABZYSQogAAAABAAAgCUwUgCgEQkAGCCIoGBAAMIAABwQNABAA=}#} 所以 A  . ……5分 3 2bc 2sinBsinC （2）由正弦定理可知  ， ……7分 a sinA 2bc 2 3 2 2 3 5 3 即  [2sinBsin( B)] ( sinB cosB) a 3 3 3 2 2 2 21 3   sin(B)，其中tan ( )， ……9分 3 5 2  2bc 2 21 故当B 时， 的最大值为 . 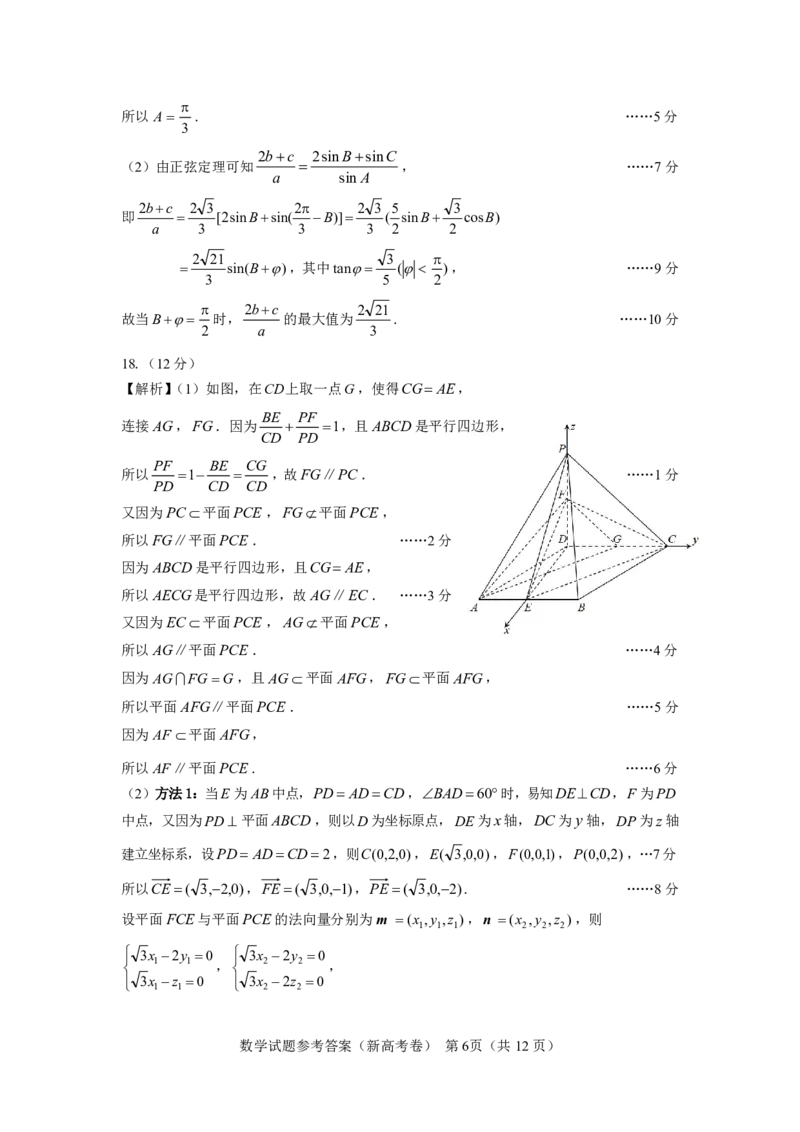……10分 2 a 3 18.（12分） 【解析】（1）如图，在CD上取一点G，使得CGAE， BE PF 连接AG，FG．因为  1，且ABCD是平行四边形， CD PD PF BE CG 所以 1  ，故FG∥PC． ……1分 PD CD CD 又因为PC平面PCE，FG平面PCE， 所以FG∥平面PCE． ……2分 因为ABCD是平行四边形，且CGAE， 所以AECG是平行四边形，故AG∥EC． ……3分 又因为EC平面PCE，AG平面PCE， 所以AG∥平面PCE． ……4分 因为AGFGG，且AG平面AFG，FG平面AFG， 所以平面AFG∥平面PCE． ……5分 因为AF 平面AFG， 所以AF∥平面PCE. ……6分 （2）方法1：当E 为AB中点，PD ADCD，BAD60时，易知DECD，F 为PD 中点，又因为PD平面ABCD，则以D为坐标原点，DE为x轴，DC为y轴，DP为z轴 建立坐标系，设PD ADCD2，则C(0,2,0)，E( 3,0,0)，F(0,0,1)，P(0,0,2)，…7分 所以CE( 3,2,0)，FE( 3,0,1)，PE( 3,0,2). ……8分 设平面FCE与平面PCE的法向量分别为m (x ,y ,z )，n (x ,y ,z )，则 1 1 1 2 2 2   3x 2y 0   3x 2y 0  1 1 ， 2 2 ，   3x z 0   3x 2z 0 1 1 2 2 数学试题参考答案（新高考卷） 第6页（共12页） {#{QQABZYSQogAAAABAAAgCUwUgCgEQkAGCCIoGBAAMIAABwQNABAA=}#}3 3 3 不妨取x  3，x  3，则m ( 3, ,3)，n ( 3, , )， ……10分 1 2 2 2 2 mn 13 所以cos m,n  ， ……11分 m n 190 21 169 21 190 21 故二面角PCEF 的正弦值为 1  ，正切值为  . ……12分 190 190 13 13 190 方法2：过D作DM  EC，垂足为M ，分别连 P 接PM ，FM ，ED． 因为PD平面ABCD，EC 平面ABCD， F 所以PD EC． ……7分 D C 因为PD，DM 是平面PDM 内两相交直线， M 所以EC 平面PDM ． ……8分 A E B 因为PM 平面PDM ，FM 平面PDM ， 所以EC PM ，EC FM ，即PMF 就是 二面角PCEF 的平面角．设PMF ，PMD1，FMD2．……9分 BE PF 因为E 为AB的中点，  1，底面ABCD是平行四边形， CD PD 所以F 是PD中点． 设PD ADCD2， 因为BAD60，易知DECD，且ED 3， 所以EC CD2ED2  7． ……10分 ED 21 所以sinECD  ， EC 7 2 3 所以DM 2sinECD  ． 7 PD 7 FD 7 所以tan1  ，tan2  ． ……11分 DM 3 DM 2 3 tan1tan2 21 所以tantan(12)  ， 1tan1tan2 13 21 即二面角PCEF 的正切值为 ． ……12分 13 数学试题参考答案（新高考卷） 第7页（共12页） {#{QQABZYSQogAAAABAAAgCUwUgCgEQkAGCCIoGBAAMIAABwQNABAA=}#}19.（12分） 【解析】（1）因为数列{a }的各项均为正数，故M 0， n n M 由2a M  M M 可得，2a  n1 1，即2a a 1. ……2分 n n n1 n n n n1 M n 所以有2(a 1)a 1，故{a 1}是公比为2，首项为a 12的等比数列， ……4分 n n1 n 1 所以a 1(a 1)2n1，a 2n1. ……6分 n 1 n （2）方法1：由（1）可知，M (21)(221)(2n1) ……7分 n 1 ≤ 21222n ……9分 2 n2 n  1 22 2 ． ……10分 n2  n 1 n2 n 所以log M ≤log 22 2 (  1)log 2n2n2. ……12分 2 n 2 2 2 2 n 方法2：由（1）可知，log M log (2i 1) ……7分 2 n 2 i1 n log (2i1) ……8分 2 i2 n n (2n)(n1) log 2i 2i2 n2 n2． 2 2 i2 i2 ……10分 当n1时，log M n2 n2， ……11分 2 n 所以log M ≤n2n2. ……12分 2 n 20.（12分） 【解析】（1）设事件A 表示共有n(n0,1,2,3,4)次投中，事件B表示第二次没投中，……1分 n P(BA ) 则P(B A ) 2 ……2分 2 P(A ) 2 1 1 1 C2   2 3 22 2  1 . ……3分 C2 1  1 2 4 22 22 （2）方法1：根据题意有X 0,1,2,3，X 0,1,2，X X 2,1,0,1,2,3， 1 2 1 2 1 1 1 则P(X X 2)P(X 0)P(X 2)   1 2 1 2 23 22 32 数学试题参考答案（新高考卷） 第8页（共12页） {#{QQABZYSQogAAAABAAAgCUwUgCgEQkAGCCIoGBAAMIAABwQNABAA=}#}5 P(X  X  1)  P(X  0)P(X 1) P(X 1)P(X  2)  1 2 1 2 1 2 32 5 P(X X 0)P(X 0)P(X 0)P(X 1)P(X 1)P(X 2)P(X 2) 1 2 1 2 1 2 1 2 16 5 P(X X 1)P(X 1)P(X 0)P(X 2)P(X 1)P(X 3)P(X 2) 1 2 1 2 1 2 1 2 16 5 P(X X 2)P(X 2)P(X 0)P(X 3)P(X 1) 1 2 1 2 1 2 32 1 1 1 P(X X 3)P(X 3)P(X 0)   . ……5分 1 2 1 2 23 22 32 1 5 5 5 5 1 1 所以E(X X )(2) (1) 0 1 2 3  . ……7分 1 2 32 32 16 16 32 32 2 1 1 方法2：因为X ~B(3, )，X ~B(2, )， ……4分 1 2 2 2 1 3 1 所以E(X )3  ，E(X )2 . ……5分 1 2 2 2 2 又因为X ，X 互相独立， 1 2 1 所以E(X X )E(X )E(X ) . ……7分 1 2 1 2 2 1 i(i1) （3）根据题意可知P(i)C2  . ……8分 i 2i 2i1 k1 P(X k) ，k2,3,,n1， ……9分 2k 1 2 n2 n1 1 2 n1 P(X n)1(   ) 1(   )， 22 23 2n1 2n 22 23 2n 1 2 n1 1 1 1 1 1 n n1 记S    ，则S 2(S  S )     1 ， n 22 23 2n n n 2 n 21 22 2n1 2n 2n 2n n1 n1 n 故P(X n)   . ……10分 2n 2n 2n1 n1 n1 i(i1) n(n1) 所以E(X) kP(X k)nP(X n)2   . ……11分 2i1 2n1 k2 i2 n(n1) 又因为 2n1  2n ，且当n≥2时， 2n ≥1， 2P(n2) n2 n2 n1 i(i1) n(n1) n1 n2 所以E(X)2   ≥2  P(i)2P(n2)2  P(i) . ……12分 2i1 2n1 i2 i2 i2 21.(12分) 【解析】（1）当k  2时，l:y 2(x2)，把x3代入得y 2，即A(3, 2)， …1分 9 2 将A代入C的方程有，  1①， ……2分 a2 b2 数学试题参考答案（新高考卷） 第9页（共12页） {#{QQABZYSQogAAAABAAAgCUwUgCgEQkAGCCIoGBAAMIAABwQNABAA=}#}且由双曲线的几何性质可知a2b24②， ……3分 x2 由①，②得，a23，b21，故C的方程为  y2 1. ……4分 3 （2）设A(x,y)，B(x ,y )，且l:yk(x2)，l与C的方程联立有： 1 1 2 2 12k2 12k23 (13k2)x212k2x12k230，则x x  ，xx  ，① ……6分 1 2 3k21 1 2 3k21 4k k2 所以 y  y k(x x )4k  ，y y k2[x x 2(x x )4] ．② 1 2 1 2 3k2 1 1 2 1 2 1 2 3k2 1 ……7分 y yx yx y x 直线OB的方程为y 2 x，故D ( 1 2,y)，P ( 1 2 2 1,y). ……8分 1 1 x y 2y 2 2 2 2yy 2k(y x  y x ) 2[x x (x x )] OP的方程为y 1 2 x，与l方程联立有：x 1 2 2 1  1 2 1 2 ， yx yx k(y x  y x )2y y x x 4 1 2 2 1 1 2 2 1 1 2 1 2 3 3 k 将①代入得x ，即Q( ，  ). ……9分 2 2 2 |OP| y |BF | y 方法1：所以  1 ，  2 ． ……10分 |PQ| k |BQ| k y  y  1 2 2 2 y y 要证 OP BQ  PQ BF ，只需证 1  2 ，即证4y y k(y  y )，③ k k 1 2 1 2 y  y  1 2 2 2 由②知③成立，所以OP BQ  PQ BF ． ……12分 方法2：由题设可知A，B，F，Q四点共线， 3 3 7 42k2 24k26 18k26 且(x  )(2x )(x 2)(x  ) (x x )2xx 6   0， 1 2 2 1 2 2 2 1 2 1 2 3k21 3k21 3k21 3 (x  )(2x ) 故 AQ BF  1 2 2 1，即 AQ  BQ . ……11分 AF  BQ 3 AF BF (x 2)(x  ) 1 2 2 PQ AQ PQ AQ BQ 由OF∥AP可知，  ，故   ， OP  BQ  PQ  BF . ……12分 OP AF OP AF BF 22.（12分） x x a 1 【解析】（1）设 f(x)alnxea，则 f(x)  ea . ……1分 x a 曲线C 与C 没有公共点等价于 f(x)没有零点. 1 2 1 当a≥e时， f(1)ea 0，且 f(a)alnae≥0， f(x)存在零点，不合题意；……2分 a a2 a 1 x a2 3e3 当0ae时，0 a， f(x)  ea 在(0,) 单调递减，且 f( ) 0， 3 x a 3 a e a2 a 1 x 0 f(a)1 0，则存在唯一x ( ,a)，使得 f(x )0，即  ea 0， a 0 3 0 x a 0 数学试题参考答案（新高考卷） 第10页（共12页） {#{QQABZYSQogAAAABAAAgCUwUgCgEQkAGCCIoGBAAMIAABwQNABAA=}#}x 0 a2 x 进一步可知，ea  ，lnx 2lna 0. ……3分 x 0 a 0 当0 x x 时， f(x)0， f(x)单调递增，当xx 时， f(x)0， f(x)单调递减， 0 0 x a2 a2 故 f(x)≤ f(x )a(2lna 0) 2alna(x  )2a(lna1)0，符合题意. 0 0 a x x 0 0 综上，a的取值范围是(0,e). ……4分 （2）（i）记题设的直线为l，由题意可知l与x轴不垂直. jt 假设it  js，则l的斜率k  1． ……5分 is 由yalnx得 y a ， a 1 ，即ia， jalna x i x 1 x 1 s 由 y ea得y ea， ea 1 ，即salna，ta． ……6分 a a jt alnaa 所以k   1，矛盾． is aalna 综上，it js． ……7分 s ea a s s （ii）由k  及(1 )ea a(lni1)，可得asi(lni1)．若ie，则asi(lni1)0， a i a s ea a e a as，且由  可得  ，故ae，这与0ae矛盾，故ie. a i a e 易知i0，t0，当0ie时，sai(1lni)0，故sa0，is0. ……8分 1 s a a2 a a 当ie时，由k  ea  ，得saln a(2ln lni)a(2ln 1)， a i i i i a 2a a a a 所以isia(2ln 1)i( ln  1)，其中0 1. i i i i i 设g(x)2xlnxx1(0 x1)，则g(x)2lnx3. 3 3   当0 xe 2时，g(x)0，g(x)单调递减，当e 2  x1时，g(x)0，g(x)单调递增， 3 3 3    所以g(x)≥g(e 2)12e 2 12e10，此时也有is(12e 2)i0. ……9分 由asi(lni1)可得isai(2lni)，设h(x)x(2lnx)，则h(x)1lnx， 当0 xe时，h(x)0，h(x)单调递增，当xe时，h(x)0，h(x)单调递减， is 所以当xe时，h(x)h(e)e，故isae2e， 2. ……10分 e 数学试题参考答案（新高考卷） 第11页（共12页） {#{QQABZYSQogAAAABAAAgCUwUgCgEQkAGCCIoGBAAMIAABwQNABAA=}#}s s j ailnisea s s as 另有   ，设ailnisea 2iea a(ilni 2a)，将sai(lni1)代入， i t s i iea s s a a 有ailnisea 2iea a(ai)( lni)，当0ie，由上可知iae，有a(ai)( lni)0， i i a s j 当ie，由上可知aei，也有a(ai)( lni)0，故  2. i i t is s j 综上，0 2  . ……12分 e i t 数学试题参考答案（新高考卷） 第12页（共12页） {#{QQABZYSQogAAAABAAAgCUwUgCgEQkAGCCIoGBAAMIAABwQNABAA=}#}