数学答案_2024-2025高二（7-7月题库）_2024年10月试卷_1010宁夏石嘴山市第一中学2024-2025学年高二上学期9月月考_宁夏回族自治区石嘴山市第一中学2024-2025学年高二上学期9月月考数学试题

2024-2025 9 1 2 3 4 5 6 7 8 9 10 A D A D D C D CD ABCD BC 11 AD 1 12． x 1 2 y 1 2 1 13． /0.5 14．4 2 15. （1）由题知， c a = 3 3 , a = 3 c , b = 2 c ， 所以椭圆 C 为 x 3 c 2 2 + 2 y c 2 2 = 1  2 3 2,  ，由点 3 在椭圆上得   3 4 c 2 + 3 2 c 2 = 1 解得 c 2 = 2 ，故椭圆方程为 x 6 2 + y 4 2 = 1 （2）设 P ( 0 , t ) , A ( x 1 , y 1 ) , B ( x 2 , y 2 ) ， 由  2 x 6y + = 2 y 4 k x + = 1 1 ，得 ( 2 + 3 k 2 ) x 2 + 6 k x − 9 = 0 ,  = 3 6 k 2 + 3 6 ( 2 + 3 k 2 ) = 1 4 4 k 2 + 7 2  0 , 所以 x 1 + x 2 = − 2 6 + k 3 k 2 , x 1 x 2 = − 2 + 9 3 k 2 ， 所以 PBPM =PB(PA+AM)=PBPA+PBAM =PBPA =(x,y −t)(x ,y −t) 1 1 2 2 =xx +(kx +1−t)(kx +1−t) 1 2 1 2 =(1+k2)xx +k(1−t)(x +x )+(1−t)2 1 2 1 2 9 6k =(1+k2)(− )+k(1−t)(− )+(1−t)2 2+3k2 2+3k2 {#{QQABRYaUogAgQIIAARhCEwHaCAEQkAECCQgOAAAAMAABQBFABAA=}#}= − 9 + 2 (1 − t 2 2 ) + + 3 ( k 3 2 t 2 − 1 2 ) k 2 ， 3t2−12 −9+2(1−t)2 1 = t= 所以 ，解得 ， 3 2 4 1 63 P(0, ) − 所以存在定点 ，使得 为定值 . 4 PBPM 16 16. （1）圆 C : x 2 + y 2 + a x − b y = 0 化为标准方程，即  x + a 2  2 +  y − b 2  2 = a 2 + 4 b 2 ， 则因为圆 C 关于直线 y = − 2 x 对称，所以 b 2 = − 2  − a 2  ，所以 b = 2 a ， 因为圆 C 过点(0,8)，所以 82−b8=0 ，所以 b=8 ， 得 a = 4 ，所以圆 C 方程为 C : x 2 + y 2 + 4 x − 8 y = 0 ， 圆心坐标为 ( − 2 , 4 ) ，半径为 2 5 ， 故点 C 到直线 x + 2 y − 1 6 = 0 −2+8−16 =2 5 的距离为 5 ， 所以 C 与直线 x + 2 y − 1 6 = 0 相切， （2）设直线 l 方程为 y = k ( x − 1 ) ，即 k x − y − k = 0 ， 设圆心 C 到直线 l 的距离为 d = ( 2 5 ) 2 − 2 2 = 4 ， −2k−4−k =4 所以 k2+1 ， 24 k =0,k = 得 7k2+24k=0 ，所以 7 ， {#{QQABRYaUogAgQIIAARhCEwHaCAEQkAECCQgOAAAAMAABQBFABAA=}#}所以直线 l 的方程为 y = 0 或 y = 2 4 7 ( x − 1 ) ． 即 y = 0 或 2 4 x − 7 y − 2 4 = 0 ． 17. 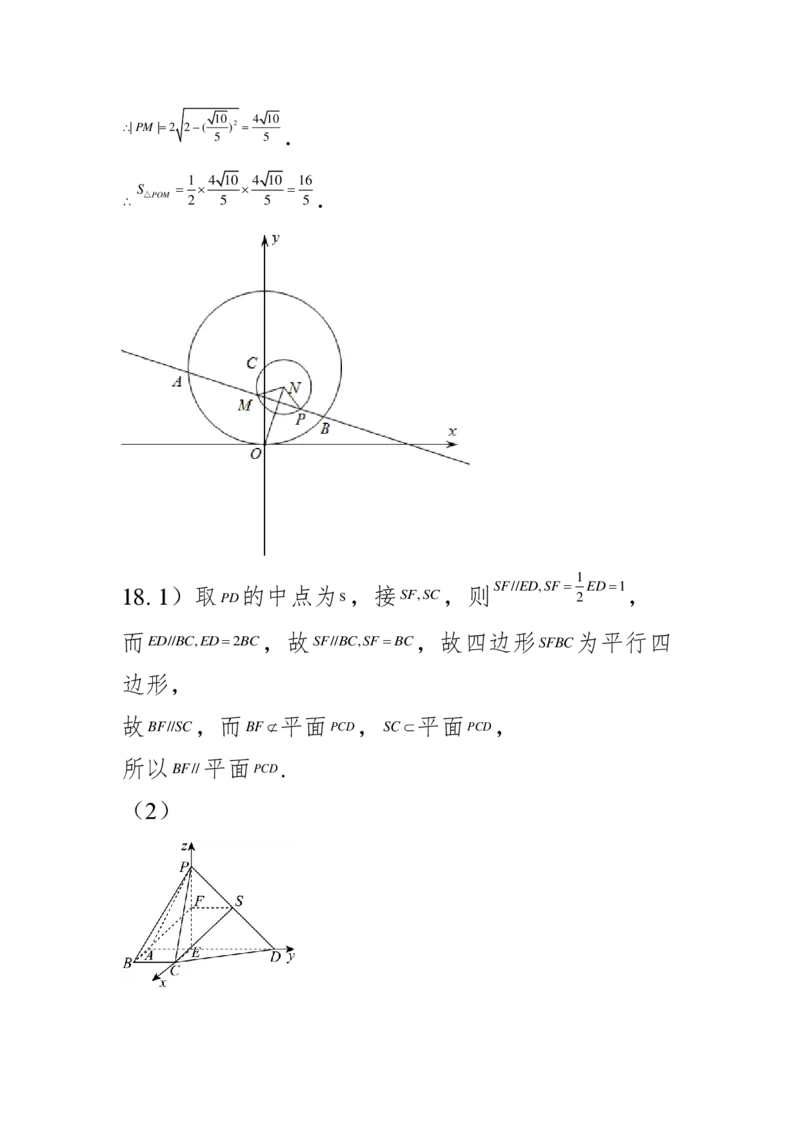（1）由圆C:x2+y2−8y=0，即𝑥2 + (𝑦 − 4)2 = 16，  圆 C 的圆心坐标为 C ( 0 , 4 ) ，半径 r = 4 ． 设 M ( x , y ) ，则 C M = ( x , y − 4 ) ， M P = ( 2 − x , 2 − y ) ． 由题意可得 C M  M P = 0 ，即 x ( 2 − x ) + ( y − 4 ) ( 2 − y ) = 0 ． 整理得 ( x − 1 ) 2 + ( y − 3 ) 2 = 2 ．  M 的轨迹方程是 ( x − 1 ) 2 + ( y − 3 ) 2 = 2 ． （2）由（1）知 的轨迹是以点 M N (1 , 3 ) 为圆心， 2 为半 径的圆， 由于 | O P |= | O M | ， 故 O 在线段 P M 的垂直平分线上， 又 P 在圆 N 上， 从而 O N ⊥ P M ． k =3 ， ON  直线 的斜率为 l − 1 3 ． 1 y−2=− (x−2) 直线 的方程为 ，即  PM 3 x + 3 y − 8 = 0 ． 则 O |−8| 4 10 = 到直线 l 的距离为 12+32 5 ． |11+33−8| 10 = 又 N 到 l 的距离为 10 5 ， {#{QQABRYaUogAgQIIAARhCEwHaCAEQkAECCQgOAAAAMAABQBFABAA=}#} | P M |= 2 2 − ( 1 5 0 ) 2 = 4 1 5 0 ．  S △ P O M = 1 2  4 1 5 0  4 1 5 0 = 1 6 5 ． 18. 1）取 P D 的中点为 S ，接 S F , S C 1 SF//ED,SF = ED=1 ，则 ， 2 而 E D //B C , E D = 2 B C ，故 S F //B C , S F = B C ，故四边形 S F B C 为平行四 边形， 故 B F //S C ，而 B F  平面 P C D ， S C  平面 P C D ， 所以 B F // 平面 P C D . 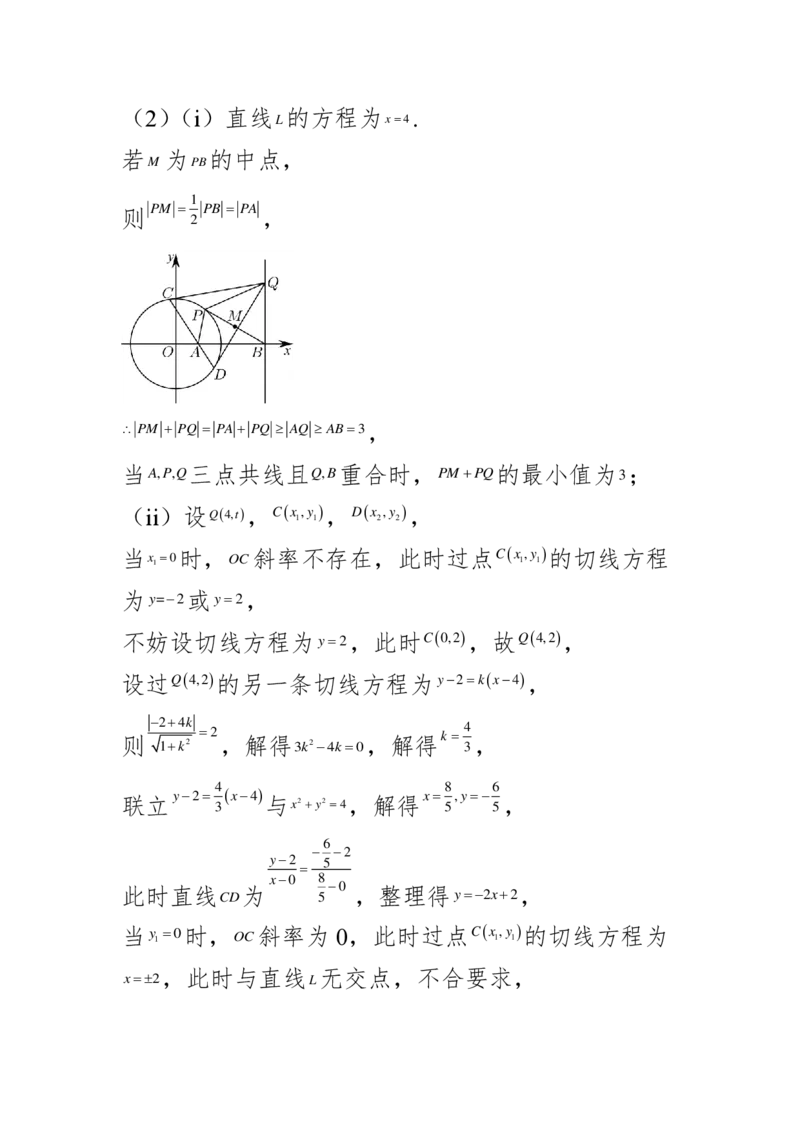（2） {#{QQABRYaUogAgQIIAARhCEwHaCAEQkAECCQgOAAAAMAABQBFABAA=}#}因为 E D = 2 ，故 A E = 1 ，故 A E //B C , A E = B C ， 故四边形 A E C B 为平行四边形，故 C E //A B ，所以 C E ⊥ 平面 P A D ， 而 P E , E D  平面 P A D ，故 C E ⊥ P E , C E ⊥ E D ，而 P E ⊥ E D ， 故建立如图所示的空间直角坐标系， 则 A ( 0 , − 1 , 0 ) , B ( 1 , − 1 , 0 ) , C ( 1 , 0 , 0 ) , D ( 0 , 2 , 0 ) , P ( 0 , 0 , 2 ) ， 则 P A = ( 0 , − 1 , − 2 ) , P B = ( 1 , − 1 , − 2 ) , P C = ( 1 , 0 , − 2 ) , P D = ( 0 , 2 , − 2 ) , 设平面 P A B 的法向量为 m = ( x , y , z ) ， 则由  m m   P P A B = = 0 0 可得  − x y − − y 2 − z 2 = z 0 = 0 ，取 m = ( 0 , − 2 ,1 ) ， 设平面 P C D 的法向量为n=(a,b,c)， 则由  n n   P P C D = = 0 0 可得  a 2 − b 2 − b 2 = c = 0 0 ，取 n = ( 2 ,1 ,1 ) ， −1 30 cosm,n= =− 故 5 6 30 ， 故平面 与平面 PAB P C D 30 夹角的余弦值为 30 19. 1）设 P ( x , y ) ，则由题意 A ( 1 , 0 ) , B ( 4 , 0 ) ， 根据题意可知 P P A B = 1 2 ，  2 P A = P B ， 2 (x−1)2+y2 = (x−4)2+y2 ， 故曲线 E 的方程为： x2+y2 =4 ； {#{QQABRYaUogAgQIIAARhCEwHaCAEQkAECCQgOAAAAMAABQBFABAA=}#}（2）（i）直线 的方程为 L x = 4 . 若 M 为 P B 的中点， 则 P M = 1 2 P B = P A ，  P M + P Q = P A + P Q  A Q  A B = 3 ， 当 A , P , Q 三点共线且 Q , B 重合时， P M + P Q 的最小值为 3 ； （ii）设Q(4,t)， C ( x 1 , y 1 ) ，D(x ,y )， 2 2 当 x 1 = 0 时， O C 斜率不存在，此时过点C(x,y )的切线方程 1 1 为 y = 2 − 或 y = 2 ， 不妨设切线方程为 y = 2 ，此时 C ( 0 , 2 ) ，故Q(4,2)， 设过 Q ( 4 , 2 ) 的另一条切线方程为 y − 2 = k ( x − 4 ) ， 则 − 2 1 + + 4 k k 2 = 2 ，解得 3 k 2 − 4 k = 0 ，解得 k = 4 3 ， 联立 y − 2 = 4 3 ( x − 4 ) 与 x 2 + y 2 = 4 ，解得 x = 8 5 , y = − 6 5 ， 此时直线 C D 为 y x − − 2 0 = − 8 5 6 5 − − 0 2 ，整理得 y = − 2 x + 2 ， 当y =0时， 1 O C 斜率为 0，此时过点C(x,y )的切线方程为 1 1 ，此时与直线 无交点，不合要求， x=2 L {#{QQABRYaUogAgQIIAARhCEwHaCAEQkAECCQgOAAAAMAABQBFABAA=}#}当 x 1  0 且 y 1  0 时， k O C = y x 1 1 ，则过点 C ( x 1 , y 1 ) 的切线方程为 y − y 1 = − x y 1 1 ( x − x 1 ) ， 整理得 y 1 y − y 21 = − x 1 x + x 21 ，即 x 1 x + y 1 y = x 21 + y 21 ， 因为 x 21 + y 21 = 4 ，故切线方程为 x 1 x + y 1 y = 4 ， 因为 Q ( 4 , t ) 在切线方程上，故 4 x 1 + ty 1 = 4 ， 设D(x ,y )，同理可得， 2 2 4 x 2 + ty 2 = 4 则直线 C D 的方程为 4 x + ty = 4 ，过定点 A 1 , 0 ， 显然 y = − 2 x + 2 也过点 A 1 , 0 ，  C D 过定点 A 1 , 0 . {#{QQABRYaUogAgQIIAARhCEwHaCAEQkAECCQgOAAAAMAABQBFABAA=}#}