数学答案_2024-2025高二（7-7月题库）_2024年12月试卷_1203云南省玉溪市一中2024-2025学年高二上学期第二次月考_云南省玉溪市一中2024-2025学年高二上学期第二次月考数学试题PDF版含答案

玉溪一中高 2026 届第三次月考 数学参考答案 一、单项选择题：本题共8小题，每小题满分5分，共40分.在每小题给出的四个选项中，只有一项符合 题目要求，选对得5分、选错得0分． 1. 抛物线 的焦点到准线的距离为（ ） A. B. C. D. 【答案】B 【解析】抛物线 的标准方程为 ，则 ，即 ， 所以抛物线 的焦点到其准线的距离为 ．故选B. 2. 直线 的斜率是（ ） A.1 B. 1 C. 3 D. 3 【答案】B 【解析】由题意得 k 2sin2102sin301. 故选B. 3. 已知圆C： 关于直线 对称，则 的值为（ ） A. 4 B.2 C. D.4 【答案】A  m 【解析】由 x2y22xmy30 ，可得圆C的圆心为 1, .  2   m 因为圆C关于直线2xy40对称，所以由圆的对称性可知，圆心 1,  在直线2xy40上，  2  m 则2 40，解得m4，故选A. 2 4. 已知 ， ， 三点不共线，点 不在平面 内， （ ）若 ， ， ， 四点共面，则 的最大值为（ ） A. B. C. 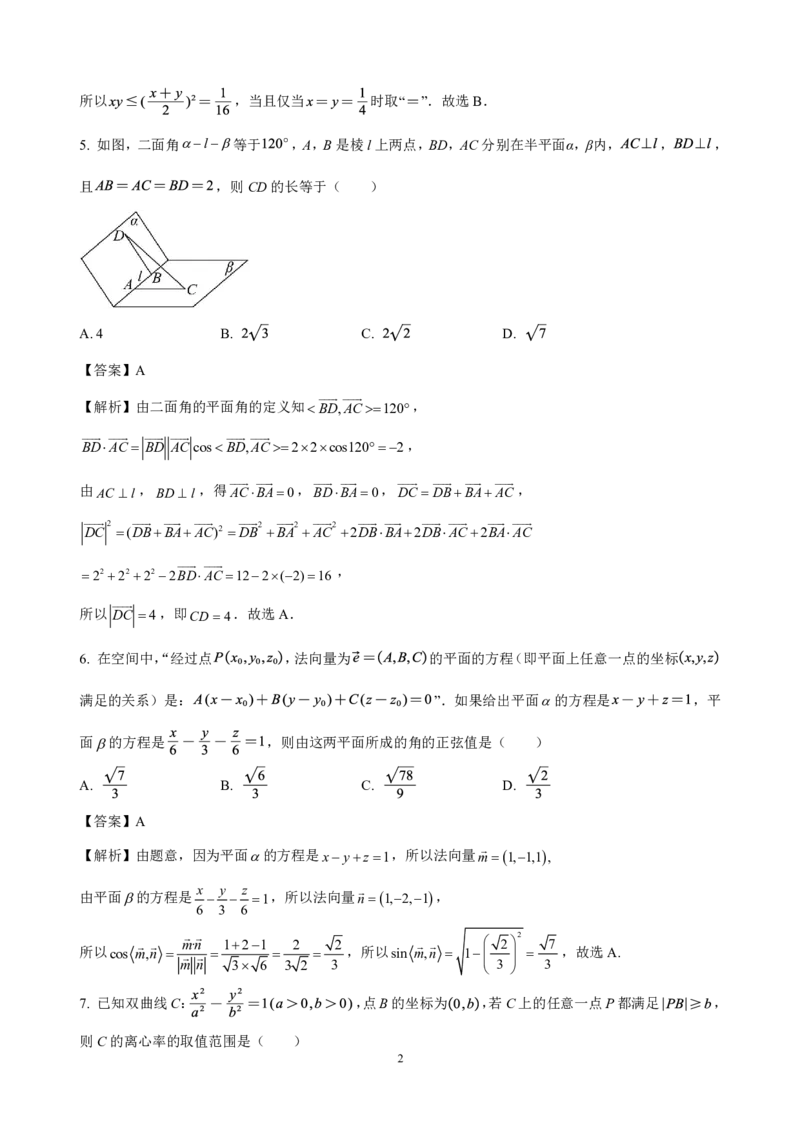D.2 【答案】B 【解析】因为 ， ， ， 四点共面，所以 ， 1所以 ，当且仅当 时取“ ”．故选B． 5. 如图，二面角l等于 ，A，B是棱l上两点，BD，AC分别在半平面α，β内， ， ， 且 ，则CD的长等于（ ） A.4 B. C. D. 【答案】A   【解析】由二面角的平面角的定义知BD,AC120，       BDAC BD ACcosBD,AC22cos1202，         由 AC l ， BDl ，得ACBA0，BDBA0，DC DBBAAC，              DC 2 (DBBAAC)2 DB 2 BA 2 AC 2 2DBBA2DBAC2BAAC   2222222BDAC122(2)16 ，  所以 DC 4，即 CD4 ．故选A． 6. 在空间中，“经过点 ，法向量为 的平面的方程（即平面上任意一点的坐标 满足的关系）是： ”．如果给出平面的方程是 ，平 面的方程是 ，则由这两平面所成的角的正弦值是（ ） A. B. C. D. 【答案】A 【解析】由题意，因为平面的方程是xyz1，所以法向量m  1,1,1, 由平面的方程是 x  y  z 1，所以法向量n  1,2,1， 6 3 6   2   m·n 121 2 2    2 7 所以cos m,n       ，所以sin m,n  1   ，故选A. m n 3 6 3 2 3  3  3 7. 已知双曲线C： ，点B的坐标为 ，若C上的任意一点P都满足 ， 则C的离心率的取值范围是（ ） 2A. B. C. D. 【答案】A x2 y2  y2 【解析】设P(x，y)，则由|PB|≥b得 x2(yb)2 b，整理得x2+y2-2by0（*），由  1得x2 a2 1  ， a2 b2  b2  c2 4a2c2 代入不等式（*）中，化简得 y2 2bya2 0恒成立，则4b2 0，即b4 a2c2，即b2 ac， b2 b2 1 5 1 5 1 5 即c2 a2 ac，可得e2e1≤0，解得 e ，又e＞1，所以1e ，故选A． 2 2 2 8. 定义：若点 在椭圆 （ ）上，则以点 P 为切点的切线方程为 ．已知椭圆C： ，点M为直线 上一个动点，过点M作椭圆C 的两条切线MA，MB，切点分别为A，B，则直线AB恒过定点（ ） A. B. C. D. 【答案】C 【解析】点M在直线x2y60上，设M(2t6,t)，A(x,y )，B(x ,y )， 1 1 2 2 x x y y x (2t6) yt 所以MA的方程为 1  1 1. 又M在MA上，所以 1  1 1 ， 3 2 3 2 x (2t6) y t x(2t6) yt ① 同理可得 2  2 1 ．由 可得AB的方程为  1 ， 3 2 3 2 ② ①② 即2x(2t6)3yt6，即(4x3y)t(12x6)0，  1 x , 所以   4x3y0, 解得   2 故直线AB恒过定点   1 , 2 .故选C. 12x60,  y 2 , 2 3  3 二、多项选择题：本题共3小题，每小题满分6分，共18分.在每小题给出的四个选项中，有多项符合题 目要求．全部选对得6分，部分选对得部分分，有选错的得0分． 9. 下列说法正确的是（ ） A. 直线 与直线 之间的距离为 B. 直线 在两坐标轴上的截距之和为 C. 将直线 绕原点逆时针旋转 ，所得到的直线为 D. 若直线 与直线 垂直，则a＝3 【答案】AC 3【解析】直线 与直线 之间的距离 ，故A正确； 对于直线 ，令 ，得 ，令 得 ， 所以直线 在两坐标轴上的截距之和为 ，故B错误； 直线 的倾斜角为 ，绕原点逆时针旋转 后，所得直线的倾斜角为 ，斜率为 ， 故C正确；若直线ax+2y1＝0与直线(a+1)x2ay+a＝0垂直，则a(a+1)4a＝0，解得a＝0或a＝3 故D不正确．故选AC． 10. 已知F是抛物线C： （ ）的焦点，直线AB经过点F交抛物线于A，B两点，则下列 说法正确的是（ ） A. 以AB为直径的圆与抛物线的准线相切 B. 若 ，则直线AB的斜率 C. 若 ， ，则 为定值p2 D. 若 ，则 的最小值为18 【答案】ACD  p  p 【解析】A：由抛物线的方程可得焦点 F ,0 ，准线方程为： x ， 2  2 设 Ax 1 ,y 1 ,Bx 2 ,y 2  ，则AB的中点 M    x 1  2 x 2, y 1  2 y 2    ，利用焦点弦的性质可得 |AB|x 1 x 2 p ， x x  p 1 1 而AB的中点M到准线的距离d  1 2   x x  p  |AB| ， 2  2 2 1 2 2  以AB为直径的圆与该抛物线的准线相切，因此A正确；  p p 1 xmy B：设直线AB的方程为 xmy ,k  ，联立  2 ，整理可得： y2 2mpy p2 0 ， 2 m  y2 2px   可得 y y 2mp,y y p2, AF 2FB,y 2y ，解得 y 2mp,y 4mp ， 1 2 1 2 1 2 2 1 1 8m2p2 p2 ，解得 m2  ，，因此B不正确，C正确； 8 (y y )2 D：若 p4，则抛物线 C: y2 8x ，不妨设x  x 0，x x  1 2 4 ， 1 2 1 2 64 4 1 |AF|4|BF|x 4x 10 4x 1042 x 1018，当且仅当 x 1,x 4 时取等号，因此 1 2 x 2 x 2 2 1 2 2 D正确．故选ACD. 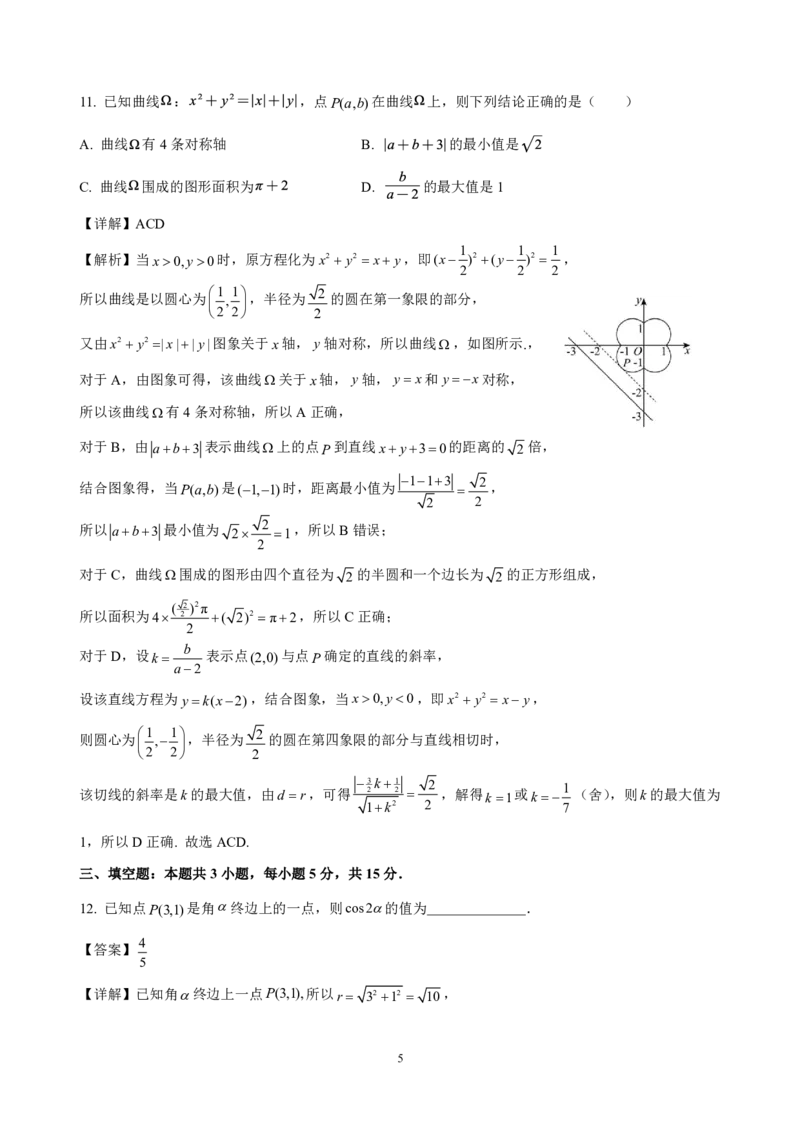411. 已知曲线 ： ，点P(a,b)在曲线 上，则下列结论正确的是（ ） A. 曲线 有4条对称轴 B. 的最小值是 C. 曲线 围成的图形面积为 D. 的最大值是1 【详解】ACD 1 1 1 【解析】当x0,y0时，原方程化为x2 y2  xy，即(x )2(y )2  ， 2 2 2 所以曲线是以圆心为   1 , 1  ，半径为 2 的圆在第一象限的部分， 2 2 2 又由x2y2 |x||y|图象关于x轴， y轴对称，所以曲线，如图所示.， 对于A，由图象可得，该曲线关于x轴， y轴，y x和yx对称， 所以该曲线有4条对称轴，所以A正确， 对于B，由 ab3 表示曲线上的点 P 到直线xy30的距离的 2 倍， 113 2 结合图象得，当P(a,b)是(1,1)时，距离最小值为  ， 2 2 所以 ab3 最小值为 2 2 1 ，所以B错误； 2 对于C，曲线围成的图形由四个直径为 2 的半圆和一个边长为 2 的正方形组成， ( 2)2π 所以面积为4 2 ( 2)2 π2，所以C正确； 2 b 对于D，设 k  表示点(2,0)与点 P 确定的直线的斜率， a2 设该直线方程为yk(x2)，结合图象，当x0,y0，即x2 y2  xy， 则圆心为   1 , 1  ，半径为 2 的圆在第四象限的部分与直线相切时， 2 2 2 该切线的斜率是k的最大值，由d r，可得  2 3k1 2  2 ，解得 k 1 或k  1 （舍），则k的最大值为 1k2 2 7 1，所以D正确. 故选ACD. 三、填空题：本题共3小题，每小题5分，共15分． 12. 已知点P(3,1)是角终边上的一点，则cos2的值为 ． 4 【答案】 5 【详解】已知角终边上一点P(3,1),所以 r 3212  10 ， 5x 3 9 4 所以cos  ，所以 cos22cos212 1 . r 10 10 5 13. 若直线 与双曲线 的左、右两支各有一个交点，则实数k 的取值范围是 ． 【答案】 【解析】当直线y＝kx+2与双曲线x2y2＝4的渐近线y＝±x平行时，k＝±1，此时直线与双曲线的其中一 支有一个交点．若直线y＝kx+2与双曲线x2y2＝4的左、右两支各有一个交点，则k的取值范围为 . 14. 已知椭圆 ，焦点为 ， （ ），过 的直线和圆 相切，并与椭圆在第一象限的图象交于点 ，且 轴，则该直线的斜率是 ， 椭圆的离心率是 . 【答案】 ； 【解析】设圆心为A，直线与圆的切点为B， 过 的直线和圆 相切的直线为 ， ， ． 将 点坐标代入 ，解得 ，即 ． 由题意可得 ，所以根据勾股定理可得 ， 由题意 ， ，故直线l的斜率 又 结合 可得 ，解 得 或 舍去 ，所以椭圆的离心率为 ．故答案为： ； ． 四、解答题：本题共5小题，共72分。解答应写出文字说明，证明过程或演算步骤． 15.（13分）已知直线l： ，圆 ． （1）若 ，求直线 截圆 所得的弦长； （2）已知直线 过定点 ，求点 的坐标及过点 的圆 的切线方程． 【答案】（1）4；（2） 或 【解析】 当 时，直线 ， 6圆 的圆心为 ，半径为 ， 则圆心 到直线 的距离为 ， 则直线 截圆 所得的弦长为 ； 对于直线 ，令 ，则 ，所以 ， 由题意易得切线的斜率存在， 则可设直线 为切点 的方程为 ，即 ， 所以 ，解得 ， 故所求切线方程为 ，即 或 ． 16.（15分）在平面直角坐标系 中，过点 的直线 与抛物线 相交于点 ， ． （1）若直线 的斜率为 ，求 的面积； （2）求证： ． 【答案】（1） ；（2）见解析 【解析】 由题意知，直线 的方程为 ， 由 ，得 ，设点 ， ，则 ， ， 所以 . 直线l的一般式方程为 ，点O到直线AB的距离 ， 所以△OAB的面积 . 证明：设 的方程为 ， 由 ，消去 得 ，设点 ， ，则 ， 所以 ，所以 ，所以 ，即 ． 17.（15分）在① ，② 这两个条件中任选一个，补充在下面问 题中，并求解（1）、（2）的答案． 7问题：在 中，三个内角A，B，C所对的边分别是a，b，c，已知_________． （1）求角C； （2）若点D满足 ，且 ，求 的面积的最大值． （注：如果选择两个条件分别解答，则按第一个解答计分．） 【答案】（1）  ；（2）3 3 3 8 【解析】(1)若选 2ab2ccosB ：由正弦定理得 2sinAsinB2sinCcosB ， ① 在 △ABC 中， sinAsinBC ，所以 2sinBCsinB2sinCcosB ， 即 2sinBcosC2cosBsinCsinB2sinCcosB ， 所以 2sinBcosC sinB ，又 B0, ，有 sinB0 ， 1  所以 cosC  ，由 C0, ，得 C  . 2 3 若选 3ccosAasinC  3b ： ② 由正弦定理得 3sinCcosAsinAsinC  3sinB ， 在 △ABC 中， sinBsinAC ， 所以 3sinCcosAsinAsinC  3sinAC 即 3sinCcosAsinAsinC  3sinAcosC 3cosAsinC ， 所以 sinAsinC  3sinAcosC ，又 A0, ，有 sinA0 ，  所以 tanC  3 ，由 C0, ，得 C  . 3  (2)不论选 或 ，均计算得 C  ， 3 由 2  A  D    D ① B  ， ② 可得 C  D  C  A    A  D  C  A   1 A  B  C  A   1 C  B  C  A    1 C  B   2 C  A  ， 3 3 3 3 两边平方可得 C  D  2  1 C  B  2  4 C  A  2  4 C  B  C  A  ， 9 9 9 1 4 4 即 1 a2 b2 abcosC ， 9 9 9 所以 9a2 4b2 2ab6ab ，当且仅当 a2b 时取“=”， 3 1 3 3 所以 ab 2 ，所以 S △ABC  2 absinC 8 . 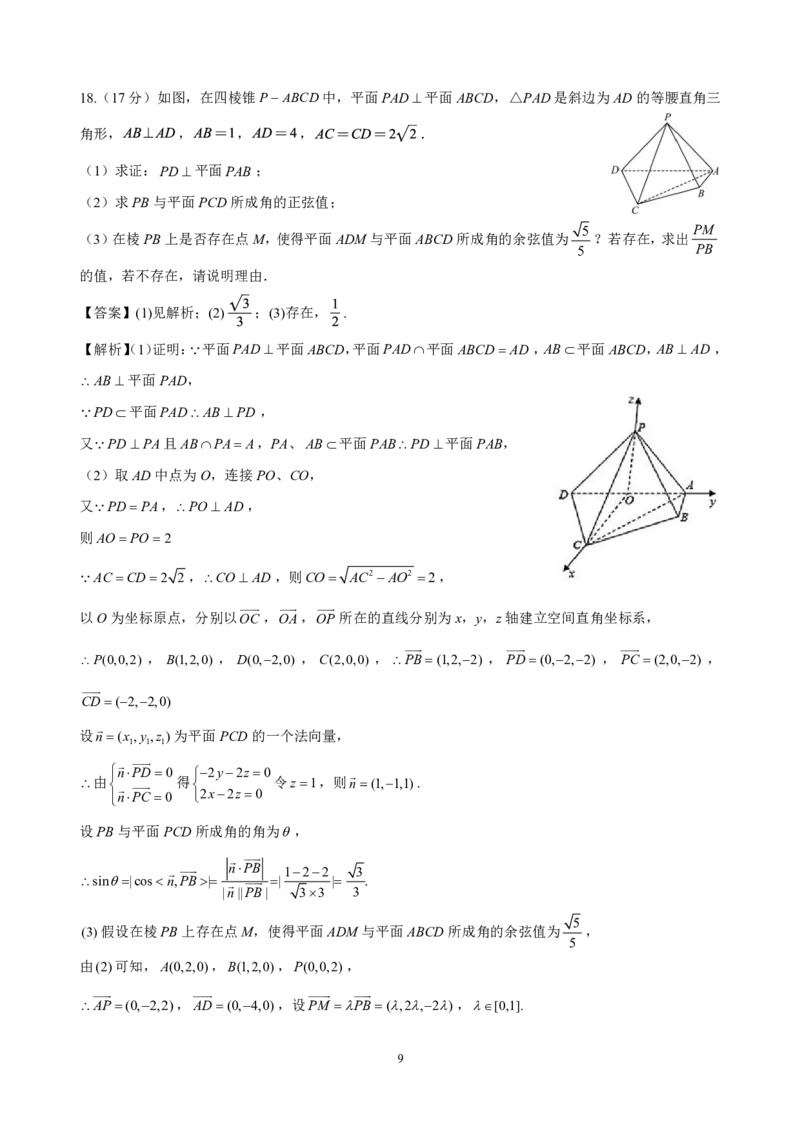818.（17分）如图，在四棱锥P ABCD中，平面PAD平面ABCD，△PAD是斜边为AD的等腰直角三 角形， ， ， ， ． （1）求证：PD平面PAB； （2）求PB与平面PCD所成角的正弦值； 5 PM （3）在棱PB上是否存在点M，使得平面ADM与平面ABCD所成角的余弦值为 ？若存在，求出 5 PB 的值，若不存在，请说明理由． 【答案】(1)见解析；(2) ；(3)存在， . 【解析】（1）证明：平面PAD平面ABCD，平面PAD平面ABCD AD ，AB平面ABCD，AB AD ， AB平面PAD， PD平面PADABPD ， 又PDPA且ABPA A，PA、AB平面PABPD平面PAB， （2）取AD中点为O，连接PO、CO， 又PDPA，PO AD， 则AOPO2 AC CD2 2，CO AD，则CO AC2AO2 2，    以O为坐标原点，分别以OC ，OA，OP所在的直线分别为x，y，z轴建立空间直角坐标系，    P(0,0,2) ， B(1,2,0) ， D(0,2,0) ， C(2,0,0) ，PB(1,2,2) ， PD(0,2,2) ， PC (2,0,2) ，  CD(2,2,0)  设n(x ,y ,z )为平面PCD的一个法向量， 1 1 1   nPD0 2y2z0  由 n  P  C  0 得 2x2z0 令z 1，则n (1,1,1). 设PB与平面PCD所成角的角为，     nPB 122 3 sin|cosn,PB|   | | . |n||PB| 33 3 5 (3)假设在棱PB上存在点M，使得平面ADM与平面ABCD所成角的余弦值为 ， 5 由(2)可知，A(0,2,0)，B(1,2,0)，P(0,0,2)，     AP(0,2,2)，AD(0,4,0)，设PM PB(,2,2)，[0,1]. 9   AM  APPM  (,22,22).  设m(x ,y ,z )为平面ADM的一个法向量， 2 2 2   nAM 0 x(22)y(22)z0 由 n    A  D  0 得 4y0 ，  则m(22,0,)，  易知平面ABCD的一个法向量为OP(0,0,2)， 设平面ADM与平面ABCD的夹角为.     mOP 2 5 1 PM 1 cos|cosm,OP|     ， ，  . m OP 2222 2 5 2 PB 2 19.（17分）已知在平面直角坐标系 中，椭圆 的中心在坐标原点 ，焦点在 轴上，焦距等于 ， 离心率为 ． （1）求椭圆 的标准方程； （2）若直线 与椭圆 交于 ， 两点，求证： 为定值； （3）记 为椭圆 的上顶点，过点 作相互垂直的两条直线 ， ，分别与椭圆 相交于 ， 两点．设 直线 的斜率为 且 ，若 ，求 的值． 【答案】（1） ；（2）见解析；（3）1或 【解析】 由已知得 ，又 ， ，又 ， 所以椭圆 的方程为 ． 依题意，设 ， ，联立直线与椭圆 有 ， 消 得： ， 当 ，即 且 时， ， ， 所以 10设 ， ，设直线 的方程为 ， 则直线 的方程为 ， 由 ，消去 得 ， 由 得 ， ， ， ， ，整理得： ， ． 或 ． 11