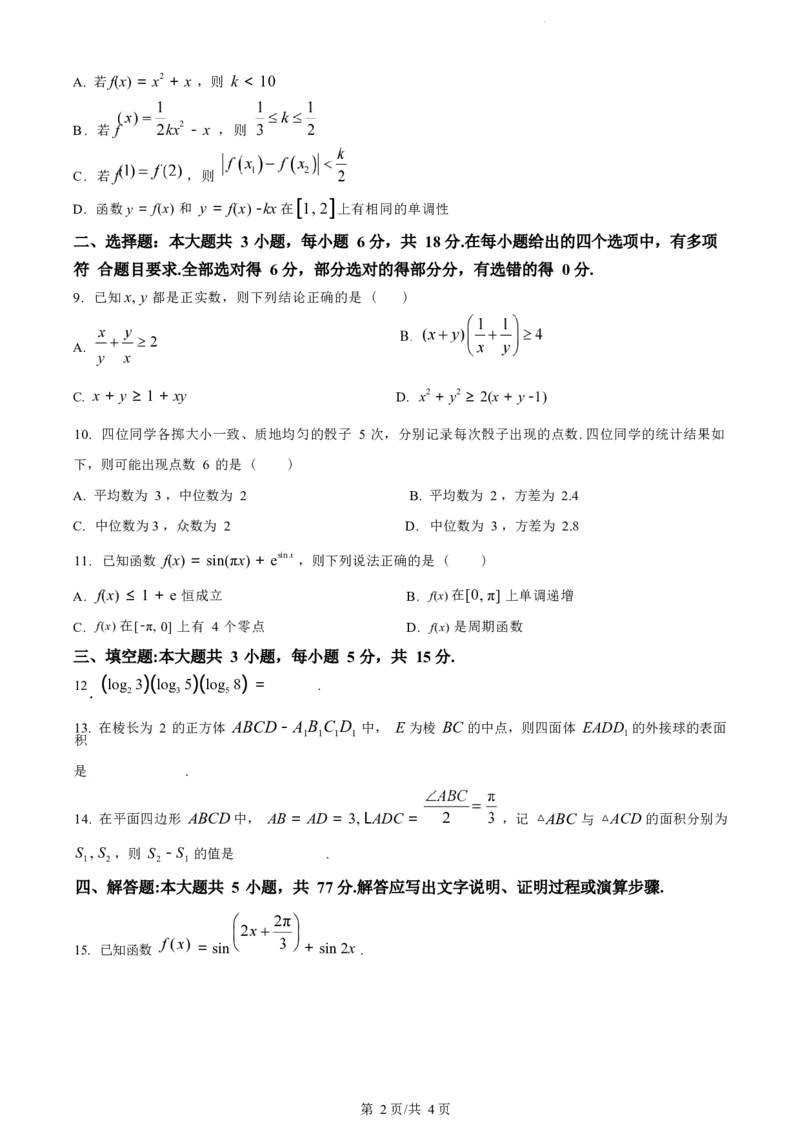文档内容
浙江省绍兴市 2023-2024 学年高二下学期 6 月期末数学试题
注意事项:
1.请将学校、班级、姓名分别填写在答卷纸相应位置上.本卷答案必须做在答卷相应位置上.
2.全卷满分 150 分,考试时间 120 分钟.
一、选择题:本大题共 8 小题,每小题 5 分,共 40 分.在每小题给出的四个选项中,只有一
项 是符合题目要求的.
= {x∣- 2 < x ≤ 2}, B = {x∣x < 2}
1. 已知集合A ,则 ( )
A. 2 ∈ B B. (C A) B = R C. A B D. A∩B ≠ ⑦
R
2. 若 z = 1+ 2i, z = 2 + i ,则 )
1 2
A. B. C. D.
3. 若函数 f(x) = 2x2 + ax -b 在 x ∈[0, 1] 上有两个不同的零点,则下列说法正确的是 ( )
A. b2 +8a > 0 B. a -b ≥ -2
C . b < 0 D. -2 ≤ a ≤ 0
- - - - -
4. 已知向量 a , 满足 | a |= 1, | |= 2, (a - ) 丄 (3a + ) ,则向量 a 与 夹角的余弦值是 ( )
B. D.
5. 已知 cos π , 则 cos 2α =
B. C. D.
6. 将编号为 1 ,2 ,3 ,4 ,5 ,6 的 6 个小球放入编号为 1 ,2 ,3 ,4 的 4 个盒子中,每个盒子至少放 1 个
小
球,则不同的放法种数是 ( )
A. 2640 B. 2160 C. 1800 D. 1560
7. 设 A, B 为两个随机事件 则P(B ∣A) = ( )
3 7 5 1
A. B. C. D.
4 12 12 4
8. 已知函数f(x) 的定义域为[1, 2],对定义域内任意的 x , x ,当 x ≠ x 时,都有 f (x ) -f (x ) < k x -
1 2 1 2 1 2 1
x ,
2
则下列说法正确的是 ( )
第 1页/共 4页A. 若f(x) = x2 + x ,则 k < 10
B. 若 f kx2 - x ,则
C. 若f ,则
D. 函数y = f(x) 和 y = f(x) -kx 在[1, 2]上有相同的单调性
二、选择题:本大题共 3 小题,每小题 6 分,共 18 分.在每小题给出的四个选项中,有多项
符 合题目要求.全部选对得 6 分,部分选对的得部分分,有选错的得 0 分.
9. 已知x, y 都是正实数,则下列结论正确的是 ( )
A.
y x
C. x + y ≥ 1 + xy D. x2 + y2 ≥ 2(x + y -1)
10. 四位同学各掷大小一致、质地均匀的骰子 5 次,分别记录每次骰子出现的点数. 四位同学的统计结果如
下,则可能出现点数 6 的是 ( )
A. 平均数为 3 ,中位数为 2 B. 平均数为 2 ,方差为 2.4
C. 中位数为3 ,众数为 2 D. 中位数为 3 ,方差为 2.8
11. 已知函数 f(x) = sin(πx) + esin x ,则下列说法正确的是 ( )
A. f(x) ≤ 1 + e 恒成立 B. f(x) 在[0, π] 上单调递增
C. f(x) 在[-π, 0] 上有 4 个零点 D. f(x) 是周期函数
三、填空题:本大题共 3 小题,每小题 5 分,共 15 分.
12 (log 3)(log 5)(log 8) = .
. 2 3 5
13. 在棱长为 2 的正方体 ABCD - A B C D 中, E 为棱 BC 的中点,则四面体 EADD 的外接球的表面
积 1 1 1 1 1
是 .
14. 在平面四边形 ABCD中, AB = AD = 3, LADC = ,记 △ABC 与 △ACD 的面积分别为
S , S ,则 S - S 的值是 .
1 2 2 1
四、解答题:本大题共 5 小题,共 77 分.解答应写出文字说明、证明过程或演算步骤.
15. 已知函数 = sin + sin 2x .
第 2页/共 4页求 f
(2)求f(x) 的单调递增区间.
16. 有A 和B 两道谜语,张某猜对 A 谜语的概率为 0.8 ,猜对得奖金 10 元;猜对B 谜语的概率为 0.5 ,猜
对得 奖金 20 元.每次猜谜的结果相互独立.
(1)若张某猜完了这两道谜语,记张某猜对谜语的道数为随机变量 X ,求随机变量 X 的分布列与期望;
(2)现规定:只有在猜对第一道谜语的情况下,才有资格猜第二道.如果猜谜顺序由张某选择,为了获得更
多的奖金,他应该选择先猜哪一道谜语?
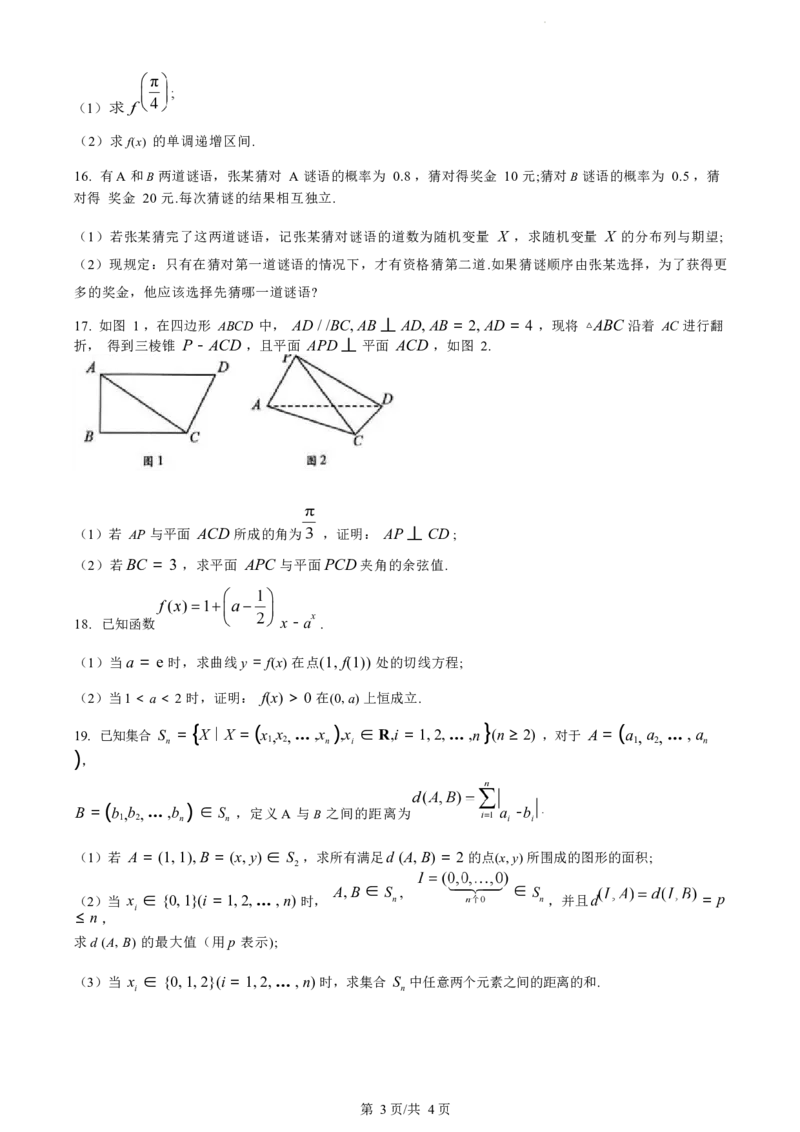
17. 如图 1 ,在四边形 ABCD 中, AD / /BC, AB 丄 AD, AB = 2, AD = 4 ,现将 △ABC 沿着 AC 进行翻
折, 得到三棱锥 P - ACD ,且平面 APD 丄 平面 ACD ,如图 2.
(1)若 AP 与平面 ACD 所成的角为 ,证明: AP 丄 CD ;
(2)若BC = 3 ,求平面 APC 与平面PCD夹角的余弦值.
x
18. 已知函数 x - a .
(1)当a = e 时,求曲线y = f(x) 在点(1, f(1)) 处的切线方程;
(2)当1 < a < 2 时,证明: f(x) > 0 在(0, a) 上恒成立.
19. 已知集合 S = {X∣X = (x ,x , … ,x ),x ∈ R,i = 1, 2, … ,n } (n ≥ 2) ,对于 A = (a , a , … , a
n 1 2 n i 1 2 n
)
,
B = (b ,b , … ,b ) ∈ S ,定义A 与B 之间的距离为 a -b
1 2 n n i i
(1)若 A = (1, 1), B = (x, y) ∈ S ,求所有满足d (A, B) = 2 的点(x, y) 所围成的图形的面积;
2
A, B ∈ S , ∈ S
(2)当 x ∈ {0, 1}(i = 1, 2, … , n) 时, n n ,并且d = p
i
≤ n ,
求d (A, B) 的最大值(用p 表示);
(3)当 x ∈ {0, 1, 2}(i = 1, 2, … , n) 时,求集合 S 中任意两个元素之间的距离的和.
i n
第 3页/共 4页第 4页/共 4页