数学试题（定）_2024-2025高二（7-7月题库）_2025年05月试卷_0519四川省遂宁市射洪中学2024-2025学年高二下学期期中考试

【考试时间:2025年5月8】 射洪中学高2023级高二下学期半期考试 数学试题 命题人: 审题人: 校对: (考试时间:120分钟 试卷满分:150分) 注意事项： 1.本试卷分第Ⅰ卷和第Ⅱ卷两部分。答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。 2.回答第Ⅰ卷时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。如需改动， 用橡皮擦干净后,再选涂其他答案标号。写在本试卷上无效。 3.回答第Ⅱ卷时,将答案写在答题卡上。写在本试卷上无效。 一、选择题:(本题共8小题共40分。在每小题给出的四个选项中,只有一项是符合题目要求的) 1.函数 f xxex的单调递增区间为( ▲ ) A.,1 B.1，0  C., D.1, 2.等差数列a 的公差为2,且a a a 10,则a a a ( ▲ ) n 1 4 6 2 5 7 A.12 B.14 C.16 D.18 3.已知函数 f  x ax3bx在x1处取得极大值6,则ab ( ▲ ) A.8 B.8 C.12 D.12 4.若函数 f xlnx a 在 2，4 上为增函数,则a的取值范围为( ▲ ) x2 A.,2 B.,2 C.,8  D.,8  5.已知S 为数列a 的前n项和,且,a 2,a  1 ,则S 的值为( ▲ ) n n 1 n1 1a 2024 n A.1009 B.1010 C.1011 D.1012 6.四人相约到射洪新时代电影院观看电影《哪吒2》,恰好买到了四张连号的电影票。若甲、乙两人 必须坐在丙的同一侧,则不同的坐法种数为( ▲ ) A.12 B.16 C.20 D.24 高二数学 第 1 页 共 4 页7.若函数 f x x2lnx在区间m,m1上不单调,则实数m的取值范围为( ▲ )  2  2 2  2   A.0,  B. 1,  C. 1,0 D. 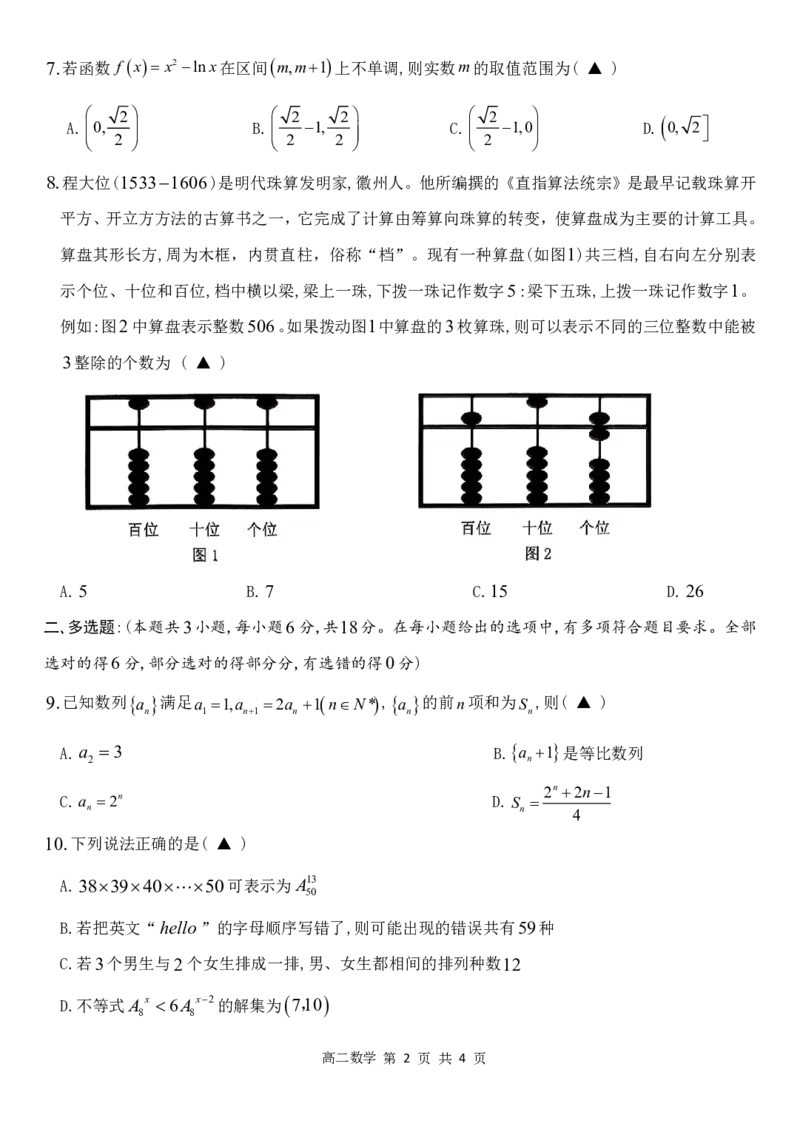0, 2         2   2 2   2  8.程大位(15331606)是明代珠算发明家,徽州人。他所编撰的《直指算法统宗》是最早记载珠算开 平方、开立方方法的古算书之一，它完成了计算由筹算向珠算的转变，使算盘成为主要的计算工具。 算盘其形长方,周为木框，内贯直柱，俗称“档”。现有一种算盘(如图1)共三档,自右向左分别表 示个位、十位和百位,档中横以梁,梁上一珠,下拨一珠记作数字5:梁下五珠,上拨一珠记作数字1。 例如:图2中算盘表示整数506。如果拨动图1中算盘的3枚算珠,则可以表示不同的三位整数中能被 3整除的个数为 ( ▲ ) A.5 B.7 C.15 D.26 二､多选题:(本题共3小题,每小题6分,共18分。在每小题给出的选项中,有多项符合题目要求。全部 选对的得6分,部分选对的得部分分,有选错的得0分) 9.已知数列a 满足a 1,a 2a 1nN*,a 的前n项和为S ,则( ▲ ) n 1 n1 n n n A.a 3 B.a 1是等比数列 2 n 2n2n1 C.a 2n D.S  n n 4 10.下列说法正确的是( ▲ ) A.38394050可表示为A13 50 B.若把英文“hello”的字母顺序写错了,则可能出现的错误共有59种 C.若3个男生与2个女生排成一排,男、女生都相间的排列种数12 D.不等式Ax 6Ax2的解集为 7，10  8 8 高二数学 第 2 页 共 4 页11.对于三次函数 f xax3bx2cxda0，给出定义: fx是函数y f x的导数, fx是函 数 fx的导数,若方程 fx0有实数解x ,则称x，f(x )为函数y f x的“拐点”.某同学经探 0 0 0 究发现:任何一个三次函数都有“拐点”；任何一个三次函数都有对称中心,且“拐点”就是对称中心， 若函数 f  x  x3ax1  aR ,则下列说法正确的是( ▲ ) A.当a 1时,函数 y f  x  拐点处的切线方程为x y10 B.当a 3时,函数 y f  x  在区间 m,m5 内存在最小值,则m的取值范围是2,1  1 2 C.若经过点 1,2 可以向曲线y f  x  作三条切线,则a的取值范围是 ，  3 3 D.对任意实数x ,直线yaxx  f x 与曲线y f  x 有唯一公共点 0 0 0 三、填空题(本题共3小题,每小题5分,共15分) 12.若C3n1C4n2,则n ▲ 。 24 24 13.已知 f x2x2ln3x,则 f1 ▲ 。 14.已知函数 f  x  x32 2x1,若过点 0,1 的两条互相垂直的直线分别与 f  x 的图象交于另 外的点A,C 和B,D,且四边形ABCD为正方形,则这两条直线的斜率之和为 ▲ 。 四、解答题:本题共5小题,共77分。解答应写出文字说明、证明过程或演算步骤。 15.(本小题满分13分) 已知函数 f  x  x2 ex。 (Ⅰ)求 f  x 的图象在点  0, f  0  处的切线方程； (Ⅱ)若g  x  f x  ( f '  x 为函数 f  x 的导函数),求g  x 在区间  0,1  上的最大值和最小值。 16.(本小题满分15分) 已知数列  a  中,a 2,S 为数列a 的前n项和,S n2 n。 n 1 n n n 1 (Ⅰ)求  a  的通项公式；(Ⅱ)若数列  b  总满足b  ,求数列b 的前n项和T 。 n n n a21 n n n 高二数学 第 3 页 共 4 页17.(本小题满分15分） 已知 f  x  xlnx,g  x  x3ax2x2. (Ⅰ)求函数 f  x  )的单调区间； (Ⅱ)若对任意的x 0, ,2f  x  g'  x 2恒成立,求实数a的取值范围。 18.(本小题满分17分) 已知数列a 的前n项和为S ,a 2,S 2S 2n1,nN*。 n n 1 n1 n S  (Ⅰ)求证:数列 n是等差数列； 2n S (Ⅱ)设b  n ,b 的前n项和为T ； n 3n n n ①求T ； ②若对任意的正整数n,不等式6T 2n恒成立,求实数的取值范围。 n n 19.(本小题满分17分) ab ab ab 对于正数a,b,且ab,定义 为a,b的对数平均值,且 ab   ,我们把上述不等 lnalnb lnalnb 2 式称为对数平均不等式。人工智能DeepSeek 给出了不等式右端的证明： a  ab ab 2ab a 2 b 1  a a (ⅰ)不妨设ab0,则  等价于 ln ,即证: ln ,令t  1,即 lnalnb 2 ab b a b b 1 b 2t1 2t1 1 4 t12 证:lnt 0 对一切t1,恒成立。记gtlnt ,则gt   0， t1 t1 t t12 tt12 所以gt在1,上单调递增，从而有gtg10证毕。 ab (Ⅰ)请参照以上方法证明: ab  lnalnb a (Ⅱ)已知函数已知函数 f  x  lnx。 x (ⅰ)讨论函数 f  x 的单调性； (ⅱ)若 f  x  f  x  2  x  x  ,证明:a2  x x ae。 1 2 1 2 1 2 (二○二五年五月印制) 高二数学 第 4 页 共 4 页