2024级高二数学期中考试答案_251222广东省汕头市金山中学2025-2026学年高二上学期期中考试（全）

2024级高二年级第一学期期中考试 数学科答案
 4 3 4 3   1
CBAD AABB 9.CD 10.ACD 11.ACD 12. 2 213.    , 3     3 ,    14.   21, 2  
15.【详解】（1）由3a 3csinB3bcosC，则3sinA 3sinCsinB3sinBcosC，
又sinAsinBCsinBcosCcosBsinC，
则有3sinBcosC3cosBsinC 3sinCsinB3sinBcosC，
即 3cosBsinC sinCsinB ，又C0,π，故sinC0，
π
则 3cosBsinB，即tanB 3，又B0,π，则B ；
3
 1   
（2）由D是AC的中点，则BD BABC ，
2
 2 1   2 1  2  2   π
则 BD  BABC   BA  BC 2 BA BC cos 
4 4 3
即 19  1 c242c  ，则c22c15c3c50，解得c3或c5（负值，舍去），
4 4
1 1 3 3 3
则S  acsin B 23  .
ABC 2 2 2 2
16.【详解】（1）由频率分布直方图得10(0.016a0.0400.0080.004)1，所以a0.032.
（2）成绩落在[50,70)内的频率为：0.160.320.48，
落在[50,80)内的频率为：0.160.320.400.88，
则第80百分位数m(70,80)，因此(m70)0.040.80.48，解得 m78，
所以成绩至少要达到78分才可以晋级.
（3）由频率分布直方图得成绩在[80,90),[90,100]的频率比为2:1，
2
因此成绩在[80,90)内抽取 64人，记为a,b,c,d，成绩在[90,100]内抽取2人，记为A,B，
3
设A“抽到的两位同学来自同一小组”，
样本空间{ab,ac,ad,aA,aB,bc,bd,bA,bB,cd,cA,cB,dA,dB,AB}，共15个样本点，
则Aab,ac,ad,bc,bd,cd,AB，共7个样本点，
7
所以选出的2人恰好来自同一小组的概率P(A) ．
15
17.【详解】（1）取CF中点H，连接OH,GH
1
∵四边形BCFE为矩形，∴点O为BF中点，∴OH //BC且OH  BC，
2
1
又∵AG BC且AG//BC，∴AGOH 且AG//OH ，
2
第 1 页 共 4 页∴四边形OHGA为平行四边形，即AO//GH ，∵GH Ì 平面GCF ，∴AO//平面GCF .
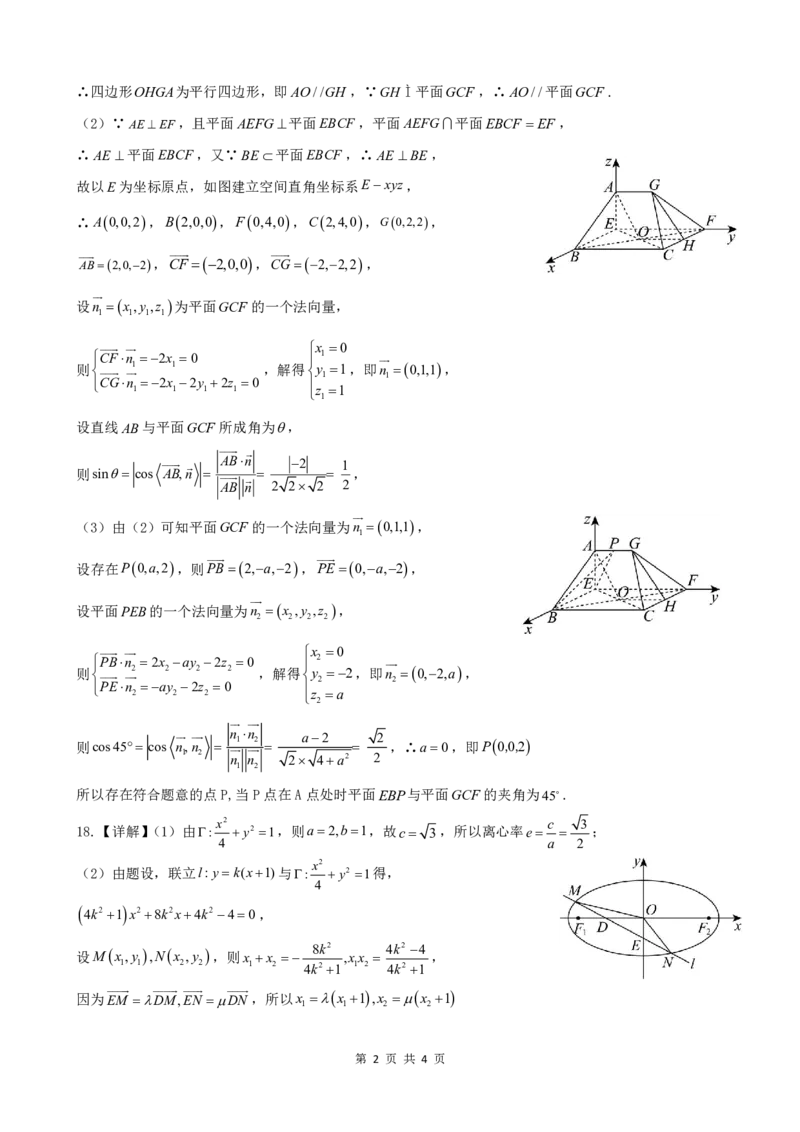
（2）∵AEEF，且平面AEFG平面EBCF，平面AEFG平面EBCF EF，
∴AE 平面EBCF，又∵BE平面EBCF，∴AE BE，
故以E为坐标原点，如图建立空间直角坐标系Exyz，
∴A0,0,2，B2,0,0，F0,4,0，C2,4,0，G0,2,2，
  
AB2,0,2，CF 2,0,0，CG 2,2,2，

设n x ,y ,z 为平面GCF的一个法向量，
1 1 1 1
  x 0
 CFn 2x 0  1 
则  1 1 ，解得y 1，即n 0,1,1，
1 1
CGn
1
2x
1
2y
1
2z
1
0 
z 1
1
设直线AB与平面GCF所成角为，
 
  ABn 2 1
则sin cos AB,n      ，
AB n 2 2 2 2

（3）由（2）可知平面GCF的一个法向量为n 0,1,1，
1
 
设存在P0,a,2，则PB2,a,2，PE0,a,2，

设平面PEB的一个法向量为n x ,y ,z ，
2 2 2 2
  x 0
 PBn 2x ay 2z 0  2 
则  2 2 2 2 ，解得y 2，即n 0,2,a，
2 2
PEn
2
ay
2
2z
2
 0 
z a
2
 
则cos45 cos n  ,n   n  1   n  2  a2  2 ，∴a0，即P0,0,2
1 2 n n 2 4a2 2
1 2
所以存在符合题意的点P,当P点在A点处时平面EBP与平面GCF的夹角为45.
x2 c 3
18.【详解】（1）由: y2 1，则a2,b1，故c 3，所以离心率e  ；
4 a 2
x2
（2）由题设，联立l:yk(x1)与: y2 1得，
4
 4k21  x28k2x4k240，
设Mx,y ,Nx ,y ，则x x 
8k2
,xx 
4k2 4
，
1 1 2 2 1 2 4k21 1 2 4k21
   
因为EM DM,EN DN ，所以x x 1,x x 1
1 1 2 2
第 2 页 共 4 页8k2
 2
x x x  x 2 4k21 2 8
 1  2 2  1 2 2  2   ；
x 1 x 1 xx x x 1 4k24 8k2 3 3
1 2 1 2 1 2  1
4k21 4k2 1
ykxm
（3）由题设，联立 ，消元得  4k21  x28kmx4m240，设Mx,y ,Nx ,y ，当
x24y2 4 1 1 2 2
Δ64k2m216  4k21  m21  0，即4k2m210时，则x x  8km ,xx  4m2 4 ，
1 2 4k2 1 1 2 4k2 1
8km 4m24 8(4k2m2m24k21)
x2x2 (x x )22xx ( )22  ，
1 2 1 2 1 2 4k21 4k21 (4k21)2
x2 x2
则 OM 2ON 2 x21 1 x21 2
1 4 2 4
2 3 x2 x2 2 24k2m2 6m2 24k2 6 2 6m2 4k2 1  6  4k2 1  ，
4 1 2  4k21 2  4k21 2
当 OM 2 ON 2为定值时，即与m2无关，故 4k210 ，得k 1 ，
2
4k21m2
此时 MN  k21 x x 24xx 4 k21  5 2m2 ，
1 2 1 2 14k2
m 2m 1 m22 m2
又点O到直线l的距离d   ，所以S  dMN  m  2m2 1，
1k2 5 MON 2 2
当且仅当 m  2m2 ，即m1时，等号成立，
经检验，此时Δ0成立，所以△MON 面积的最大值为1.
19.【详解】（1）由题可知，x1,，x2ax50即a x25  x 5 成立，
x x
令gxx 5 ,gx在  1, 5  上单调递减，在  5,  上单调递增，g  5  2 5，
x
gx

2 5,  ,a2 5，解得a2 5,a  ,2 5

．
5 1 5 1
（2）（i）原方程即为xa  x ，即a x  x ，
x x x x
 4
2x ,1 x4

令hx x 5  x 1    x
x x 6
,0x1
x
要使原方程在0,4内有两个不等实根，只需ya与yhx的图象在0,4内恰有两个交点．
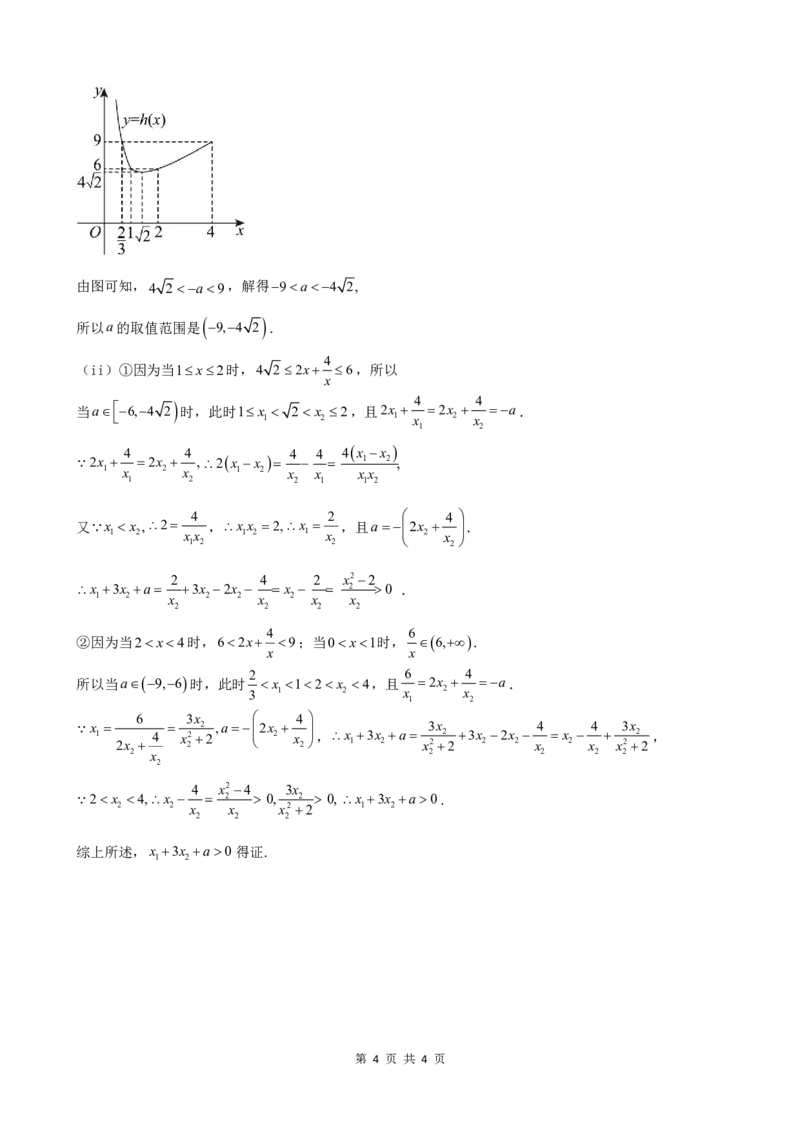
hx在  0, 2  上单调递减，在  2,4  上单调递增．h1h26,h  2  4 2,h   2 h49，
3
作如图所示的hx的图象：
第 3 页 共 4 页由图可知，4 2a9，解得9a4 2,
 
所以a的取值范围是 9,4 2 .
4
（ii）①因为当1x2时，4 2 2x 6，所以
x
 4 4
当a6,4 2 时，此时1x  2x 2，且2x  2x  a．
 1 2 1 x 2 x
1 2
4 4 4 4 4x x 
2x  2x  ,2x x    1 2 ,
1 x 2 x 1 2 x x xx
1 2 2 1 1 2
4 2  4 
又x  x ,2 ，xx 2,x  ，且a2x  ．
1 2 xx 1 2 1 x  2 x 
1 2 2 2
2 4 2 x22
x 3x a 3x 2x   x   2 0 ．
1 2 x 2 2 x 2 x x
2 2 2 2
4 6
②因为当2x4时，62x 9；当0x1时， 6,.
x x
所以当a9,6时，此时 2  x 12 x 4，且 6 2x  4 a．
3 1 2 x 2 x
1 2
6 3x  4 
x 1  2x  4  x 2 2 2 2 ,a  2x 2  x 2   ，x 1 3x 2 a x 3 2 x  2 2 3x 2 2x 2  x 4  x 2  x 4  x 3 2 x  2 2 ，
2 x 2 2 2 2
2
4 x24 3x
2 x 4,x   2  0, 2  0,x 3x a0.
2 2 x x x22 1 2
2 2 2
综上所述，x 3x a0得证.
1 2
第 4 页 共 4 页