文档内容
荆州中学2021级高三下学期第三次适应性考试
数学试题
命题人: 审题人:
一、单项选择题(本题共8道小题,每题四个选项中有且仅有一个正确答案,每小题5
分,共40分)
1.已知集合 ,其中 是实数集,集合 ,则 (
)
2.已知圆 直线 方程 则“圆 与直线 相切”是
“方程 表示的曲线为椭圆”的( )
充分非必要条件 必要非充分条件 充要条件 既非充分也非必要条件
3.同宿舍六位同学在食堂排队聚餐,其中 , , 三人两两不相邻, 和 是双胞胎,必须相邻,
则符合排队要求的方法种数为( )
4.已知 则 的值为( )
5.已知正四棱台上底面边长为 ,下底面边长为 ,体积为 ,则正四棱台的侧棱与底面所成角的正
切值为( )
6. 已知向量 满足 , , ,则 ,
A. B. C. D.
7.上周联考的数学成绩 服从正态分布 且 ,负责命题的王老师考后随
机抽取了 个学生的数学成绩,设这10个学生中得分在 的人数为 ,则随机变量 的方
差为( )8.斜率为 的直线 经过双曲线 的左焦点 ,交双曲线于 两点, 为双曲线
的右焦点且 ,则双曲线的渐近线方程为( )
A. B. C. D.
二、多项选择题(本题共3道小题,每题四个选项中至少有两个正确答案,每小题 6分,
共18分)
9. 已知 ,则( )
A. 的值为2 B. 的值为16
C. 的值为-5 D. 的值为120
10. 设△ABC的内角A,B,C的对边分别为a,b,c,恒成立条件a=3cos C,b=1. 附加条件①△ABC的面积
❑√10
取到最大值 ; 附加条件②c= .下列结论正确的是( )
2
A. B.tan C=2tan B
C.若恒成立条件和附加条件①成立,则
D.若恒成立条件和附加条件②成立,则
11.在平面直角坐标系 中,动点 与两个定点 和 连线的斜率之积等于 ,记
点 的轨迹为曲线 ,直线 : 与 交于 , 两点,则( )
A. 的方程为 B. 的离心率为
C. 的渐近线与圆 相切 D.满足 的直线 仅有1条三、填空题(本题共3道小题,每小题5分,共15分)
12.棣莫弗定理:若 为正整数,则 ,其中 为虚数
单位,已知复数 , 则 的实部为___________.
(第一个空满分2分,第二个空满分3分)
13.抛物线有如下光学性质:由焦点射出的光线经抛物线反射后平行于抛物线的对称轴;反之,平
行于抛物线对称轴的入射光线经抛物线发射后必经过抛物线的焦点.已知抛物线 的焦点为 ,
一平行于 轴的光线从点 射出,经过抛物线上的点 反射后,再经抛物线上的另一点 射出,
则直线 的斜率为___________.
14.天道酬勤,勤能补拙,努力的人得到的结果也许不尽如人意,虽然问心无愧的他们往往能平静看
待生活中的点点滴滴,后悔这个词离他们似乎很遥远,但面对不顺时,他们有时候也会反思一些细
节,情不自禁的流下悔恨的泪水。其实每个人在生活中都曾有过后悔的经历,即便是懒惰成性,不
思进取的人,遇到挫折时,他们中也会有人会反思过去的不足,即使明知悔之晚矣,也往往会流下
悔恨的泪水。某位经验丰富的班主任老师,从高一开始,一直在反复告诫自己的学生:珍惜当下,
积极进取,争做高考后无怨无悔的人,不做高考后如祥林嫂般的悔恨者。一晃三年过去了,这位班
主任老师结合学生三年的表现,调查发现,自己任教的班级勤懒生人数之比为 ,结合自己对以
前毕业于自己班的学生高考后的表现发现,勤生高考后流下悔恨的泪水的概率为0.001,而懒生高考
后流下悔恨的泪水的概率为0.020.展望本届学生高考,他清楚地知道,自己班上一定有学生会在高考
后流下悔恨的泪水,若真如该老师所料,有一位学生流下了悔恨的泪水,则这个学生恰好是一名懒
生的概率为 (结果用既约分数表示)
四、解答题(本题共5道小题,共77分)
15. (本题满分13分)
“ 数列”定义:数列 的前 项和为 ,如果对于任意的正整数 ,总存在正整数 使
则称数列 是“ 数列”。
(1)若数列 的前 项和为 求证:数列 是“ 数列”;
(2)已知数列 是“ 数列”,且数列 是首项为 ,公差小于 的等差数列,求数列
的通项公式;(3)若数列 满足: 求数列 的前 项和 。
16. (本题满分15分)
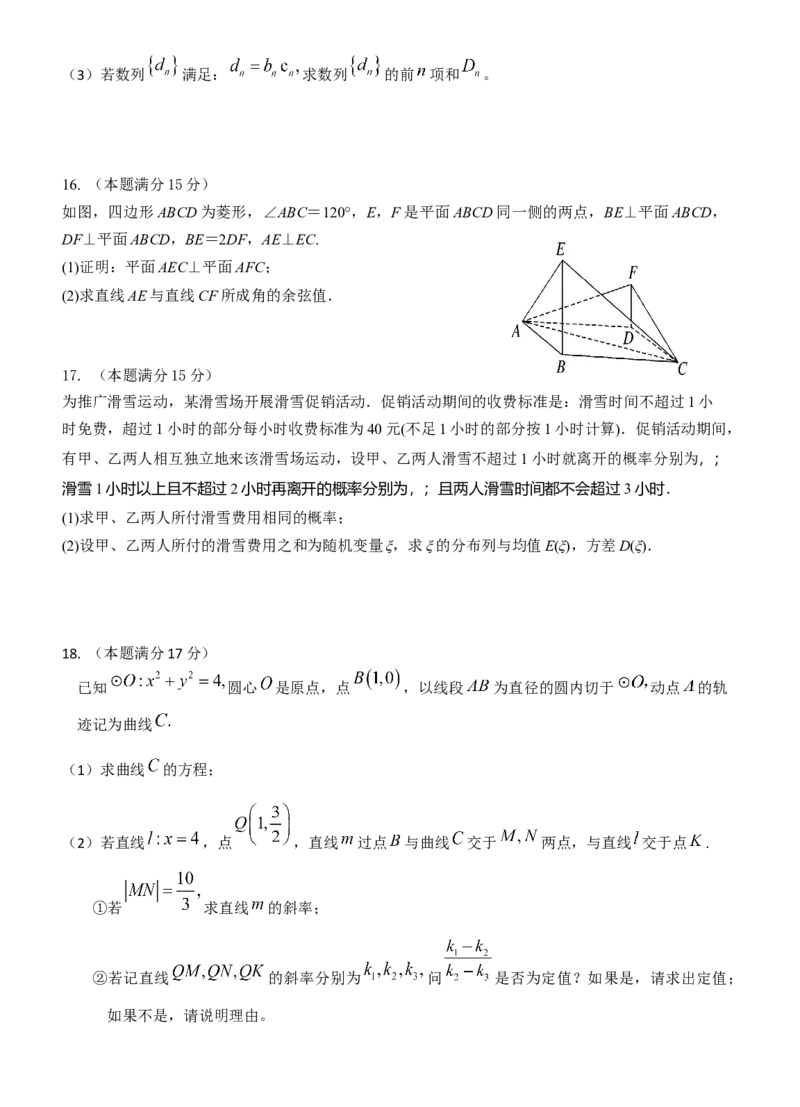
如图,四边形ABCD为菱形,∠ABC=120°,E,F是平面ABCD同一侧的两点,BE⊥平面ABCD,
DF⊥平面ABCD,BE=2DF,AE⊥EC.
(1)证明:平面AEC⊥平面AFC;
(2)求直线AE与直线CF所成角的余弦值.
17. (本题满分15分)
为推广滑雪运动,某滑雪场开展滑雪促销活动.促销活动期间的收费标准是:滑雪时间不超过1小
时免费,超过1小时的部分每小时收费标准为40元(不足1小时的部分按1小时计算).促销活动期间,
有甲、乙两人相互独立地来该滑雪场运动,设甲、乙两人滑雪不超过1小时就离开的概率分别为,;
滑雪1小时以上且不超过2小时再离开的概率分别为,;且两人滑雪时间都不会超过3小时.
(1)求甲、乙两人所付滑雪费用相同的概率;
(2)设甲、乙两人所付的滑雪费用之和为随机变量ξ,求ξ的分布列与均值E(ξ),方差D(ξ).
18. (本题满分17分)
已知 圆心 是原点,点 ,以线段 为直径的圆内切于 动点 的轨
迹记为曲线
(1)求曲线 的方程;
(2)若直线 ,点 ,直线 过点 与曲线 交于 两点,与直线 交于点 .
①若 求直线 的斜率;
②若记直线 的斜率分别为 问 是否为定值?如果是,请求出定值;
如果不是,请说明理由。19. (本题满分17分)
已知函数 ,其中 是自然对数的底数。
(1)当 时,求曲线 在点 处的切线的斜截式方程;
(2)当 时,求出函数 的所有零点;
(3)证明: 。