2024级高二数学期中考试试卷(1)_251222广东省汕头市金山中学2025-2026学年高二上学期期中考试（全）

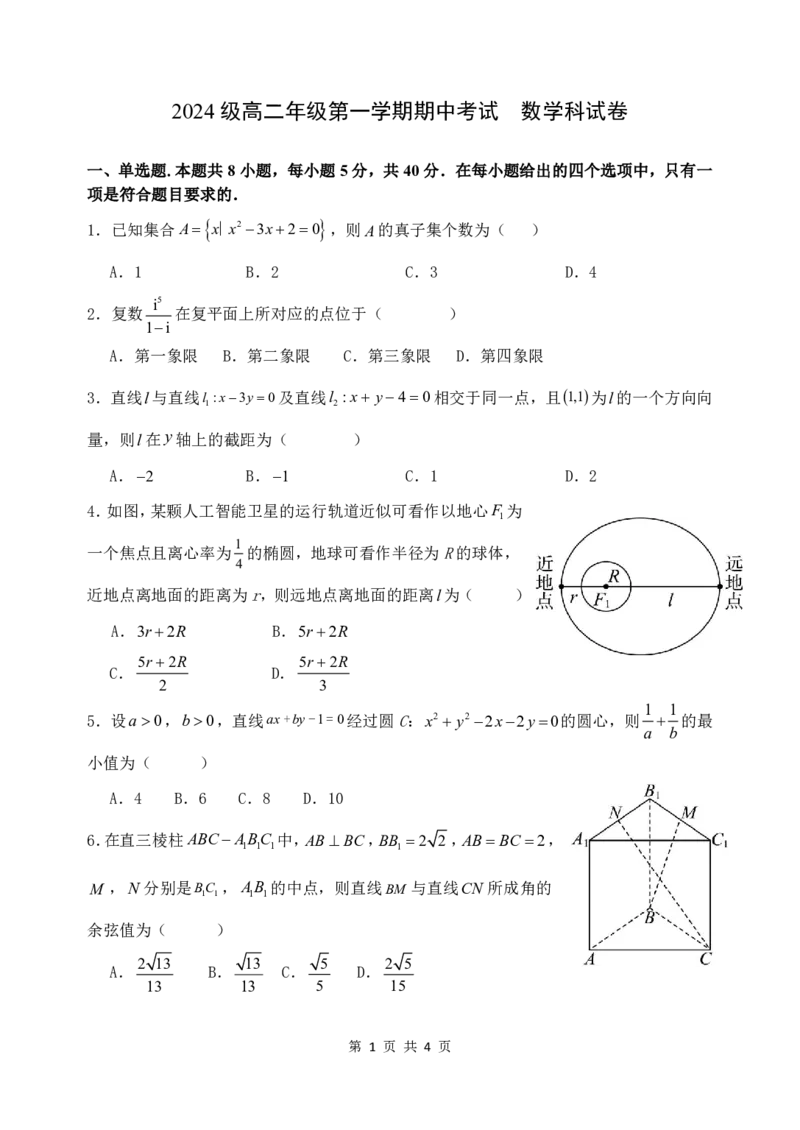
2024 级高二年级第一学期期中考试 数学科试卷 一、单选题.本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一 项是符合题目要求的． 1．已知集合A  x∣x23x20  ，则A的真子集个数为（ ） A．1 B．2 C．3 D．4 i5 2．复数 在复平面上所对应的点位于（ ） 1i A．第一象限 B．第二象限 C．第三象限 D．第四象限 3．直线l与直线l :x3y0及直线l :x y40相交于同一点，且1,1为l的一个方向向 1 2 量，则l在y轴上的截距为（ ） A．2 B．1 C．1 D．2 4．如图，某颗人工智能卫星的运行轨道近似可看作以地心F 为 1 1 一个焦点且离心率为 的椭圆，地球可看作半径为R的球体， 4 近地点离地面的距离为r，则远地点离地面的距离l为（ ） A．3r2R B．5r2R 5r2R 5r2R C． D． 2 3 1 1 5．设a0，b0，直线ax+by-1=0经过圆C：x2 y22x2y0的圆心，则  的最 a b 小值为（ ） A．4 B．6 C．8 D．10 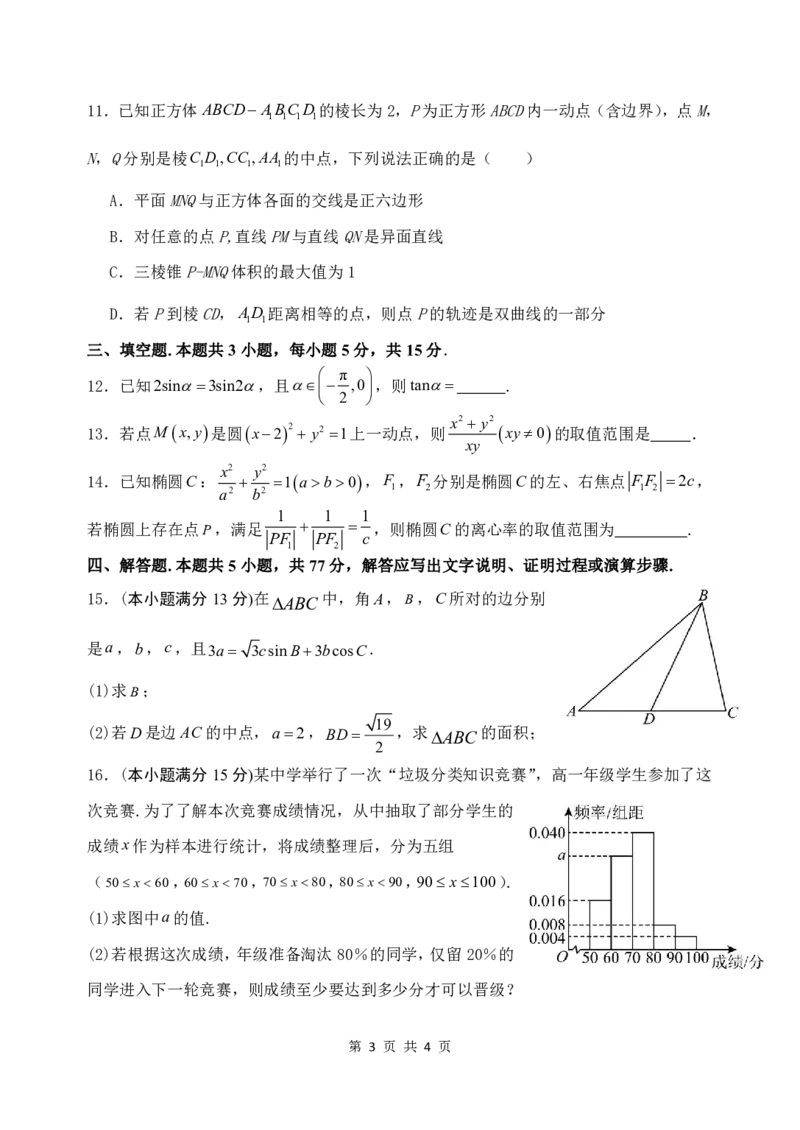6．在直三棱柱ABCABC 中，ABBC，BB 2 2，ABBC2， 1 1 1 1 M ，N 分别是BC ，AB 的中点，则直线BM 与直线CN 所成角的 1 1 1 1 余弦值为（ ） 2 13 13 5 2 5 A． B． C． D． 13 13 5 15 第 1 页 共 4 页x2 y2 7．已知双曲线C:  1m0的虚半轴长为 5 ，F 为双曲线C的左焦点，点P为 m m1 双曲线C的右支上的动点，点A的坐标为1,3，则 PF  PA的最小值为（ ） 19 A．8 B．9 C． D．10 2   8．平面内两定点M0,2和N0,2，动点Px,y，满足 PM  PN  mm 4，动点P的 轨迹为曲线E，下列命题错误的有几个（ ） ①存在m，使曲线E过坐标原点； ②曲线E关于y轴对称，但不关于x轴对称； ③若P,M,N 三点不共线，则PMN 周长最小值为 2 m4 ； ④曲线E上与M,N不共线的任意一点G关于原点对称的点为H，则四边形GMHN 的 面积不大于m. A.0个 B.1个 C.2个 D.3个 二、多选题.本题共3小题，每小题6分，共18分，在每小题给出的选项中，有多项符合 题目要求，全部选对得6分，有选错得0分，部分选对得部分分． 9．以下四个命题中，正确的是（ ） A．设A2,0，B2,0，动点P满足 ，则动点P的轨迹为双曲线 x2 y2 | |−| |= 4 B．若曲线  1表示椭圆，则2t5 5t t2 C．方程3x210x30的两根可分别作为椭圆和双曲线的离心率 x2 y2 x2 y2 D．椭圆  1与双曲线  1有相同的焦点 25 8 12 5 10．已知圆C:x22 y2 4，直线l:m1x2y1m0mR ，则（ ） A．直线l恒过定点1,1 B．当m0时，圆C上恰有三个点到直线l的距离等于1 C．直线l被圆C截得的最小弦长为2 2 D．若圆C与圆x2 y22x8ya0恰有三条公切线，则a8 第 2 页 共 4 页11．已知正方体ABCD ABCD的棱长为2，P为正方形ABCD内一动点（含边界），点M， 1 1 1 1 N，Q分别是棱CD,CC ,AA的中点，下列说法正确的是（ ） 1 1 1 1 A．平面MNQ与正方体各面的交线是正六边形 B．对任意的点P,直线PM与直线QN是异面直线 C．三棱锥P-MNQ体积的最大值为1 D．若P到棱CD，AD 距离相等的点，则点P的轨迹是双曲线的一部分 1 1 三、填空题.本题共3小题，每小题5分，共15分．  π  12．已知2sin3sin2，且 ,0，则tan .  2  x2 y2 13．若点Mx,y是圆x22 y2 1上一动点，则 xy0的取值范围是 ． xy x2 y2 14．已知椭圆C：  1ab0，F ，F 分别是椭圆C的左、右焦点 FF 2c， a2 b2 1 2 1 2 1 1 1 若椭圆上存在点P，满足   ，则椭圆C的离心率的取值范围为 . PF PF c 1 2 四、解答题.本题共5小题，共77分，解答应写出文字说明、证明过程或演算步骤. 15．(本小题满分13分)在ABC 中，角A，B，C所对的边分别 是a，b，c，且3a 3csinB3bcosC. 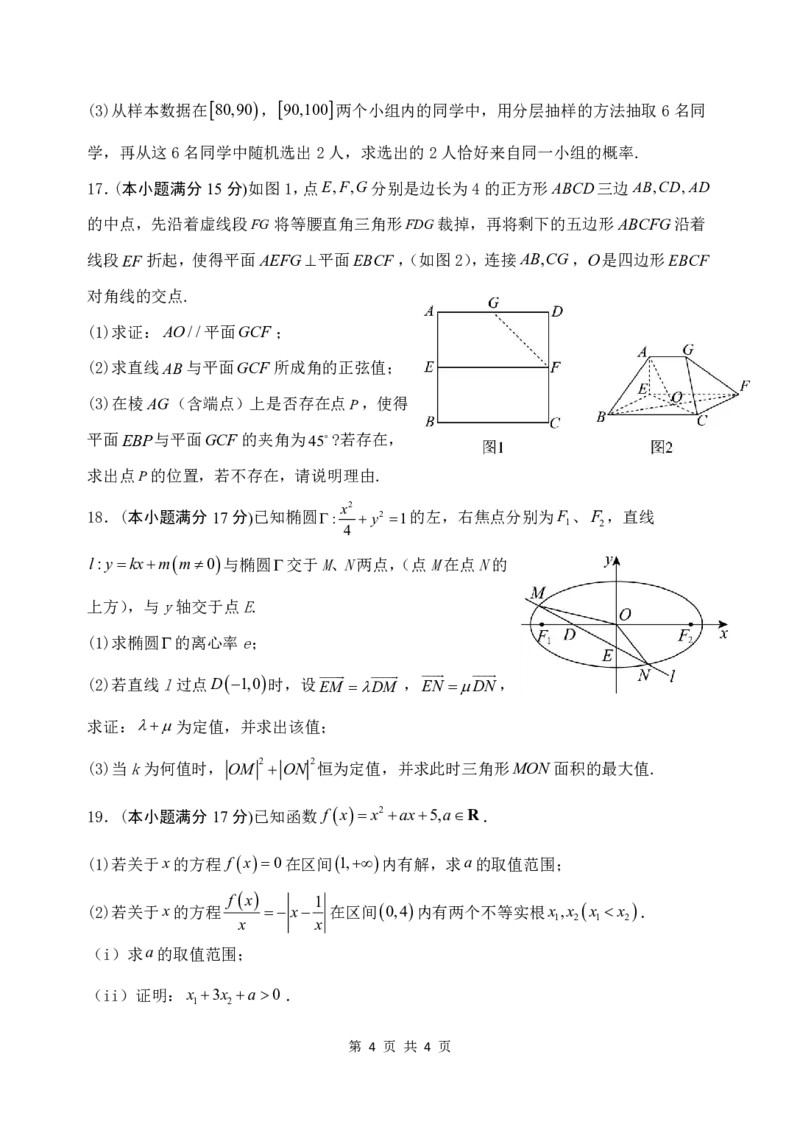(1)求B； 19 (2)若D是边AC的中点，a2，BD ，求ABC 的面积； 2 16．(本小题满分15分)某中学举行了一次“垃圾分类知识竞赛”，高一年级学生参加了这 次竞赛.为了了解本次竞赛成绩情况，从中抽取了部分学生的 成绩x作为样本进行统计，将成绩整理后，分为五组 （50x60，60x70，70x80，80x90，90 x100）. (1)求图中a的值. (2)若根据这次成绩，年级准备淘汰80％的同学，仅留20％的 同学进入下一轮竞赛，则成绩至少要达到多少分才可以晋级？ 第 3 页 共 4 页(3)从样本数据在 80,90，90,100两个小组内的同学中，用分层抽样的方法抽取6名同 学，再从这6名同学中随机选出2人，求选出的2人恰好来自同一小组的概率. 17．(本小题满分15分)如图1，点E,F,G分别是边长为4的正方形ABCD三边AB,CD,AD 的中点，先沿着虚线段FG将等腰直角三角形FDG裁掉，再将剩下的五边形ABCFG沿着 线段EF折起，使得平面AEFG平面EBCF，（如图2），连接AB,CG，O是四边形EBCF 对角线的交点. (1)求证：AO//平面GCF； (2)求直线AB与平面GCF所成角的正弦值； (3)在棱AG（含端点）上是否存在点P，使得 平面EBP与平面GCF 的夹角为45?若存在， 求出点P的位置，若不存在，请说明理由. x2 18．(本小题满分17分)已知椭圆: y2 1的左，右焦点分别为F 、F ，直线 1 2 4 l:ykxmm0与椭圆交于M、N两点，（点M在点N的 上方），与y轴交于点E. (1)求椭圆的离心率e；     (2)若直线l过点D1,0时，设EM DM ，EN DN， 求证：为定值，并求出该值； (3)当k为何值时，OM 2 ON 2恒为定值，并求此时三角形MON面积的最大值. 19．(本小题满分17分)已知函数 f xx2ax5,aR． (1)若关于x的方程 f x0在区间1,内有解，求a的取值范围； f x 1 (2)若关于x的方程  x 在区间0,4内有两个不等实根x,x x x ． x x 1 2 1 2 （i）求a的取值范围； （ii）证明：x 3x a0． 1 2 第 4 页 共 4 页