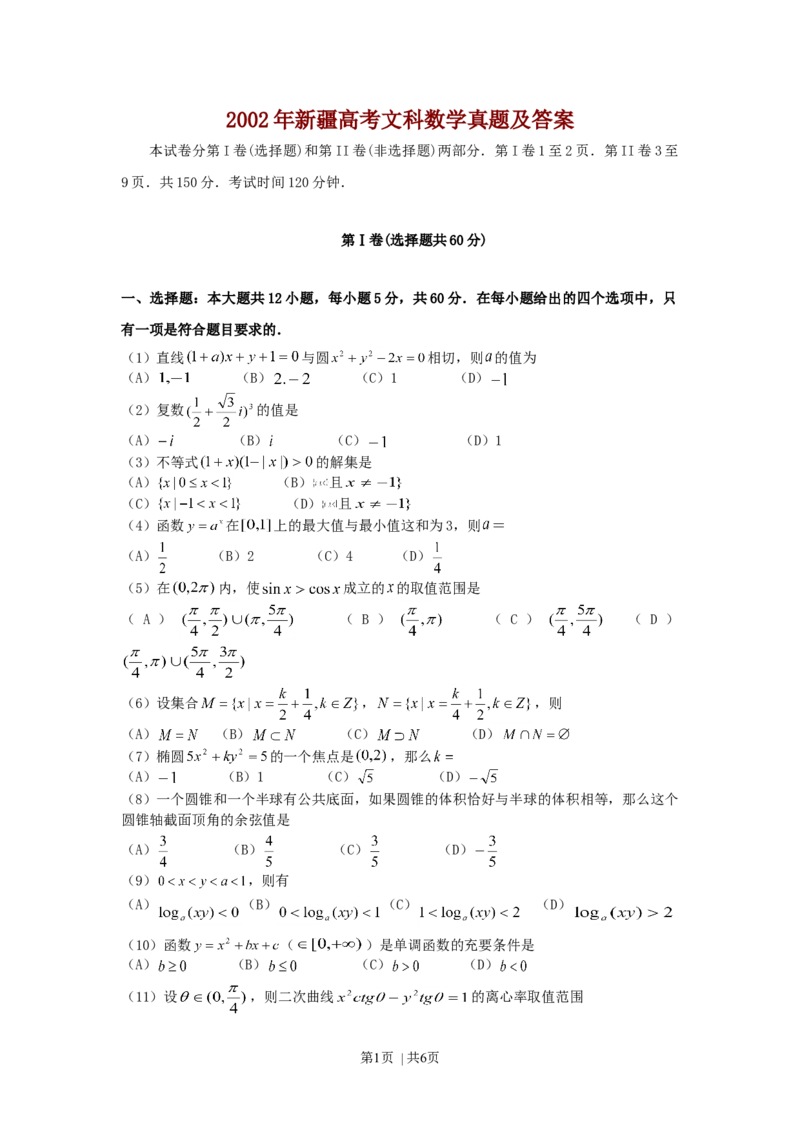文档内容
2002 年新疆高考文科数学真题及答案
本试卷分第I卷(选择题)和第II卷(非选择题)两部分.第I卷1至2页.第II卷3至
9页.共150分.考试时间120分钟.
第Ⅰ卷(选择题共60分)
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只
有一项是符合题目要求的.
(1)直线 与圆 相切,则 的值为
(A) (B) (C)1 (D)
(2)复数 的值是
(A) (B) (C) (D)1
(3)不等式 的解集是
(A) (B) 且
(C) (D) 且
(4)函数 在 上的最大值与最小值这和为3,则 =
(A) (B)2 (C)4 (D)
(5)在 内,使 成立的 的取值范围是
( A ) ( B ) ( C ) ( D )
(6)设集合 , ,则
(A) (B) (C) (D)
(7)椭圆 的一个焦点是 ,那么
(A) (B)1 (C) (D)
(8)一个圆锥和一个半球有公共底面,如果圆锥的体积恰好与半球的体积相等,那么这个
圆锥轴截面顶角的余弦值是
(A) (B) (C) (D)
(9) ,则有
(A) (B) (C) (D)
(10)函数 ( )是单调函数的充要条件是
(A) (B) (C) (D)
(11)设 ,则二次曲线 的离心率取值范围
第1页 | 共6页(A) (B) (C) (D)
(12)从正方体的6个面中选取3个面,其中有2个面不相邻的选法共有
(A)8种 (B)12种 (C)16种 (D)20种
第II卷(非选择题共90分)
二、填空题:本大题共4小题,每小题4分,共16分.把答案填在题中横线.
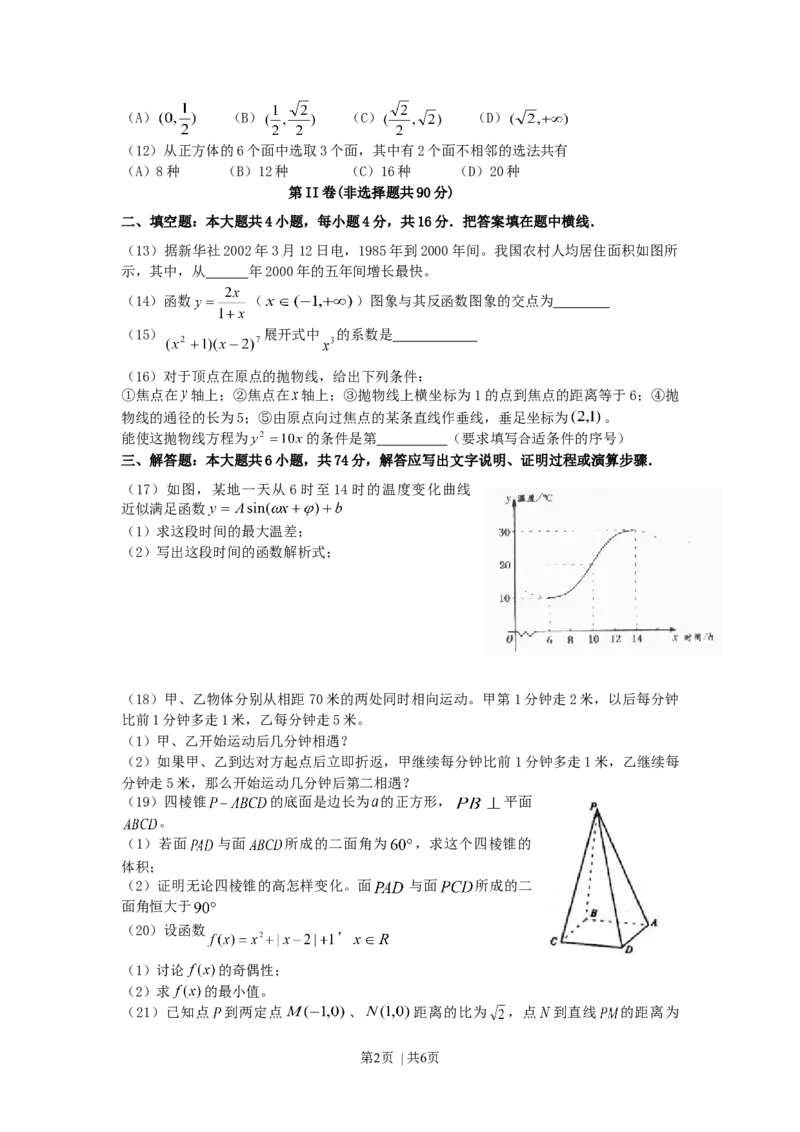
(13)据新华社2002年3月12日电,1985年到2000年间。我国农村人均居住面积如图所
示,其中,从 年2000年的五年间增长最快。
(14)函数 ( )图象与其反函数图象的交点为
(15) 展开式中 的系数是
(16)对于顶点在原点的抛物线,给出下列条件:
①焦点在 轴上;②焦点在 轴上;③抛物线上横坐标为1的点到焦点的距离等于6;④抛
物线的通径的长为5;⑤由原点向过焦点的某条直线作垂线,垂足坐标为 。
能使这抛物线方程为 的条件是第 (要求填写合适条件的序号)
三、解答题:本大题共6小题,共74分,解答应写出文字说明、证明过程或演算步骤.
(17)如图,某地一天从 6时至14时的温度变化曲线
近似满足函数
(1)求这段时间的最大温差;
(2)写出这段时间的函数解析式;
(18)甲、乙物体分别从相距70米的两处同时相向运动。甲第1分钟走2米,以后每分钟
比前1分钟多走1米,乙每分钟走5米。
(1)甲、乙开始运动后几分钟相遇?
(2)如果甲、乙到达对方起点后立即折返,甲继续每分钟比前1分钟多走1米,乙继续每
分钟走5米,那么开始运动几分钟后第二相遇?
(19)四棱锥 的底面是边长为 的正方形, 平面
。
(1)若面 与面 所成的二面角为 ,求这个四棱锥的
体积;
(2)证明无论四棱锥的高怎样变化。面 与面 所成的二
面角恒大于
(20)设函数 ,
(1)讨论 的奇偶性;
(2)求 的最小值。
(21)已知点 到两定点 、 距离的比为 ,点 到直线 的距离为
第2页 | 共6页1,求直线 的方程。
(22)(本小题满分12分,附加题满分4分)
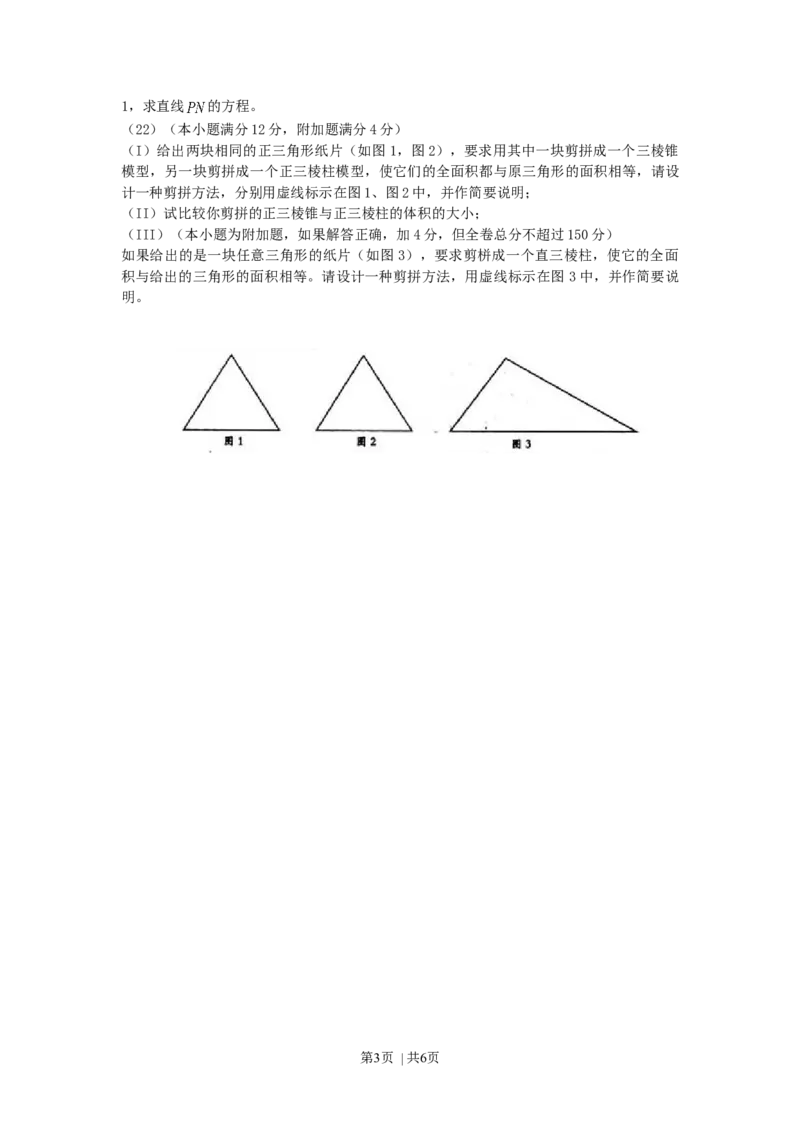
(I)给出两块相同的正三角形纸片(如图1,图2),要求用其中一块剪拼成一个三棱锥
模型,另一块剪拼成一个正三棱柱模型,使它们的全面积都与原三角形的面积相等,请设
计一种剪拼方法,分别用虚线标示在图1、图2中,并作简要说明;
(II)试比较你剪拼的正三棱锥与正三棱柱的体积的大小;
(III)(本小题为附加题,如果解答正确,加4分,但全卷总分不超过150分)
如果给出的是一块任意三角形的纸片(如图3),要求剪栟成一个直三棱柱,使它的全面
积与给出的三角形的面积相等。请设计一种剪拼方法,用虚线标示在图 3中,并作简要说
明。
第3页 | 共6页参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 D C D B C B B C D A D B
二、填空题
(13)1995 2000 (14) (15)1008 (16)②⑤
三、解答题
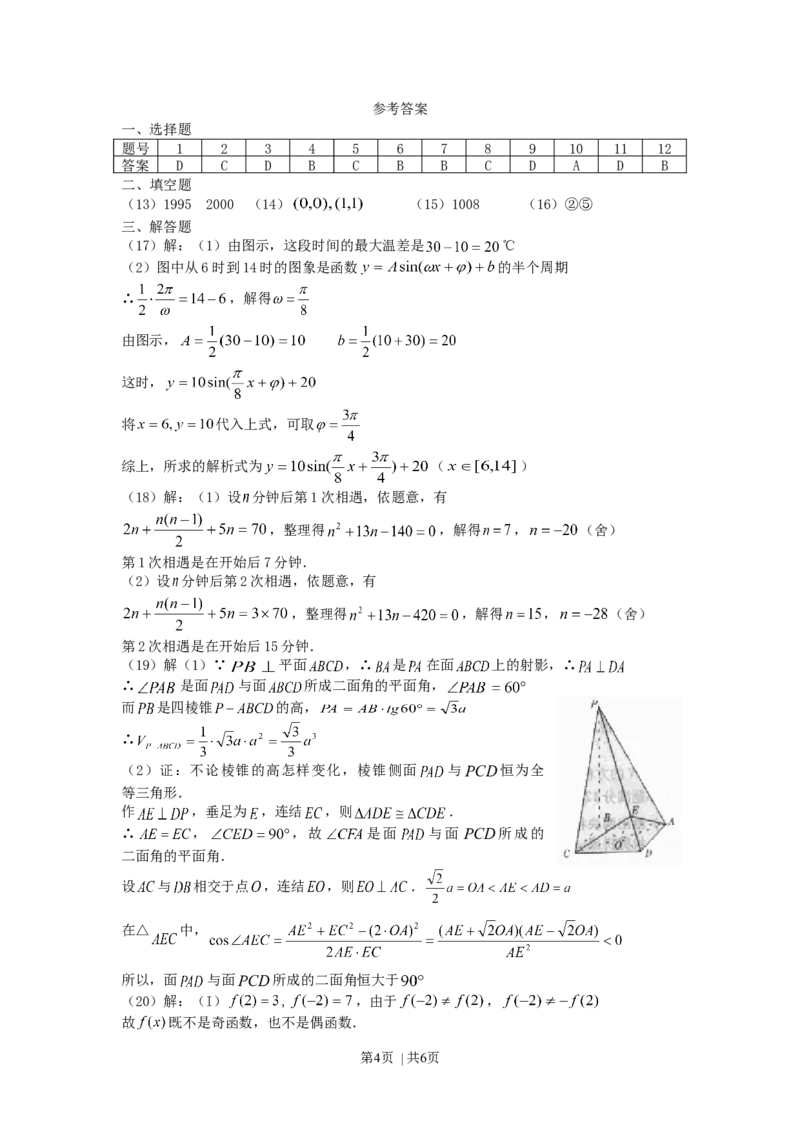
(17)解:(1)由图示,这段时间的最大温差是 ℃
(2)图中从6时到14时的图象是函数 的半个周期
∴ ,解得
由图示,
这时,
将 代入上式,可取
综上,所求的解析式为 ( )
(18)解:(1)设 分钟后第1次相遇,依题意,有
,整理得 ,解得 , (舍)
第1次相遇是在开始后7分钟.
(2)设 分钟后第2次相遇,依题意,有
,整理得 ,解得 , (舍)
第2次相遇是在开始后15分钟.
(19)解(1)∵ 平面 ,∴ 是 在面 上的射影,∴
∴ 是面 与面 所成二面角的平面角,
而 是四棱锥 的高,
∴
(2)证:不论棱锥的高怎样变化,棱锥侧面 与PCD恒为全
等三角形.
作 ,垂足为 ,连结 ,则 .
∴ , ,故 是面 与面 PCD所成的
二面角的平面角.
设 与 相交于点 ,连结 ,则 .
在△ 中,
所以,面 与面PCD所成的二面角恒大于
(20)解:(I) , ,由于 ,
故 既不是奇函数,也不是偶函数.
第4页 | 共6页(2)
由于 在 上的最小值为 ,在 内的最小值为
故函数 在 内的最小值为
(21)解:设 的坐标为 ,由题意有 ,即
,整理得
因为点 到 的距离为1,
所以 ,直线 的斜率为
直线 的方程为
将 代入 整理得
解得 ,
则点 坐标为 或
或
直线 的方程为 或 .
(22)解(I)如图1,沿正三角形三边中点连线折起,可拼得一个正三棱锥.
如图2,正三角形三个角上剪出三个相同的四边形,其较长的一组邻边边长为三角形边长
的 ,有一组对角为直角,余下部分按虚线折起,可成一个缺上底的正三棱柱,而剪出的
三个相同的四边形恰好拼成这个正三棱锥的上底.
(II)依上面剪拼方法,有 .
推理如下:
设给出正三角形纸片的边长为2,那么,正三棱锥与正三棱柱的底面都是边长为1的正三
角形,其面积为 .现在计算它们的高:
, .
所以 .
(III)如图3,分别连结三角形的内心与各顶点,得三条线段,再以这三条线段的中点为
顶点作三角形.以新作的三角形为直棱柱的底面,过新三角形的三个顶点向原三角形三边
作垂线,沿六条垂线剪下三个四边形,可心拼成直三棱柱的上底,余下部分按虚线折起,
成为一个缺上底的直三棱柱,即可得到直三棱柱.
第5页 | 共6页第6页 | 共6页