文档内容
2023—2024 学年高一第二学期开学检测考试
数学
注意事项:
1.答题前,考生务必将自己的姓名、考生号、考场号、座位号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如需改动,
用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上。写在本试卷上
无效。
3.考试结束后,将本试卷和答题卡一并交回。
4.本试卷主要考试内容:人教 A版必修第一册。
一、选择题:本大题共8小题,每小题 5分,共 40分.在每小题给出的四个选项中,只有一项是
符合题目要求的.
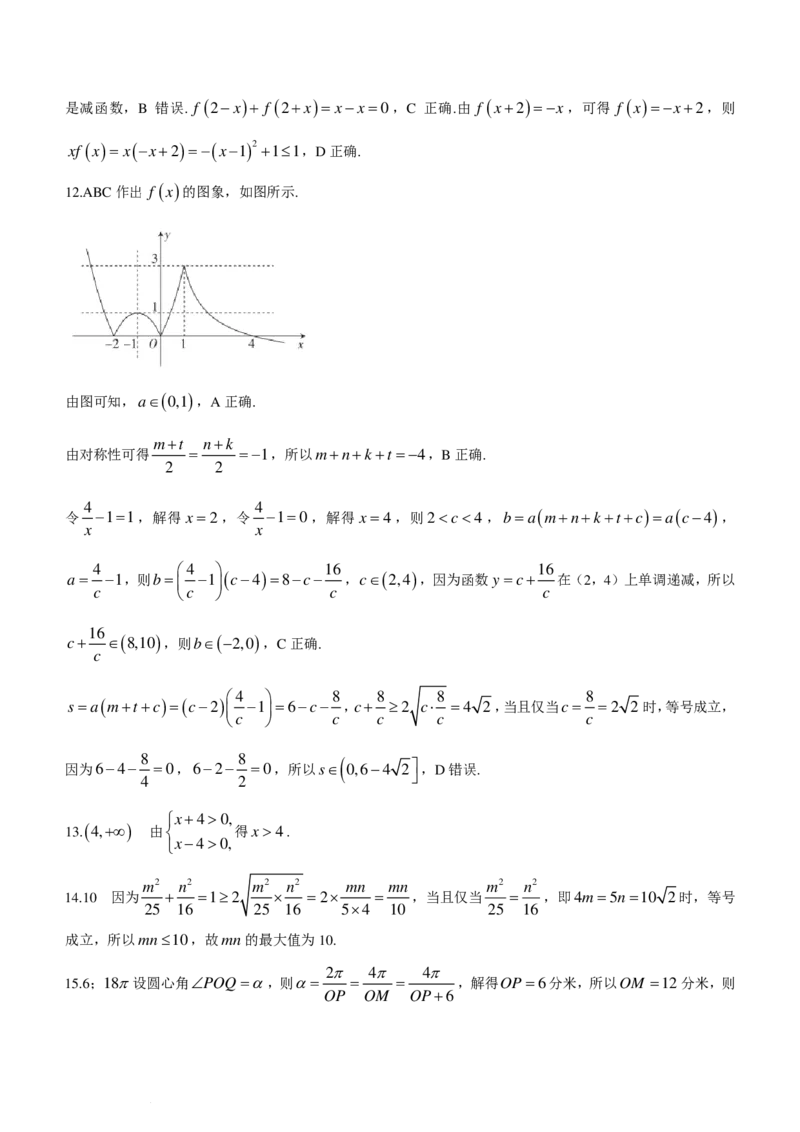
1
{ }
1.已知集合M = x −3< x<4 ,N =x x+1>0,则M N =( )
2
A.
(−3,3 )
B.
(−3,6 )
C.
(−2,4 )
D.
(−3,2 )
2.“a≥4”是“ a ≥4”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
( )
3.已知角α的终边经过点 7,7 3 ,则角α的值可能为( )
π π 2π 5π
A. B. C. D.
3 6 3 6
4.已知a =3−0.3,b=cos2,c=lg11,则( )
A.c0 )在0, 上有且只有一个最大值点(即取得最大值对应的自变量),则ω
6 3
的取值范围是( )
[ ] ( ] ( ) ( ]
A. 1,7 B. 1,7 C. 1,7 D. 4,7
( 5m−3 ) x−2m2 +1,x<1,
8.已知 f ( x )= 是R上的单调函数,则m的取值范围是( )
log x,x≥1
m
1 1 3
A.0,
(
1,2
]
B. ,
[ 2,+∞)
2 2 5
1 3 1
C. ,
( 2,+∞)
D.0,
[ 2,+∞)
2 5 2
二、选择题:本大题共4小题,每小题 5分,共 20分.在每小题给出的选项中,有多项符合题目
要求.全部选对的得 5分,部分选对的得 2分,有选错的得 0分.
9.下列命题是真命题的是( )
A.若函数 f ( x3 ) = x+2,则 f ( 8 )=4
B.“∀x∈R,x2 + x >0”的否定是“∃x∈R,x2 + x ≤0”
2
C.函数y = x3为奇函数
D.函数 f ( x )=ax−100 +log ( 2x−199 )(a >0且a≠1)的图象过定点(100,1)
a
10.若关于x的不等式ax2 −4x+2<0有实数解,则a的值可能为( )
A.0 B.3 C.1 D.-2
π 7
11. 已 知 函 数 f ( x )= Asin (ωx+ϕ) A>0,ω>0,ϕ< 的 部 分 图 象 如 图 所 示 , 若 OC = ,
2 8
tan∠NCM =2,则( )
学科网(北京)股份有限公司 π
A. f ( x )=sin πx+
8
5 3
B. f ( x )的单调递增区间为 − +k, +k ( k∈Z )
8 8
5
C. f ( x )的图象关于点 ,0对称
8
5
D. f ( x )的图象关于直线x=− 对称
8
x2 +2x ,x≤1,
12. 已 知 函 数 f ( x )= 若 m,n,k,t,c ( m1.
x
f ( m )= f ( n )= f ( k )= f ( t )= f ( c )=a,则下列结论正确的是( )
A.a∈(
0,1
)
B.m+n+k+t =−4
C.若b=mf ( m )+nf ( n )+kf ( k )+tf ( t )+cf ( c ),则b∈(−2,0 )
( )
D.若s =mf ( m )+tf ( t )+cf ( c ),则s∈ 0,6− 33
三、填空题:本大题共 4小题,每小题 5分,共 20分.把答案填在答题卡中的横线上.
13.函数 f ( x )=ln ( x+4 )−ln ( x−4 )的定义域为_____________.
m2 n2
14.若正数m,n满足 + =1,则mn的最大值为____________.
25 16
15.一扇环形砖雕如图所示,该扇环形砖雕可视为扇形OMN截去同心扇形OPQ所得的部分,已知PM =6分
米,弧MN 长为4π分米,弧 PQ长为2π分米,则OP= ____________分米,此扇环形砖雕的面积为
____________平方分米.
2x+1−1
16.若函数 f ( x )=log 在( 1,+∞)上满足 f ( f ( x )) = x恒成立,则k =____________.
2 2x +k
学科网(北京)股份有限公司四、解答题:本大题共 6小题,共 70分.解答应写出文字说明、证明过程或演算步骤.
17.(10分)
计算:
(1)2lg 5+lg2−log 27×log 2;
2 3
1
− 2
(2) 81 2 −(−sin1 )0 − ( 27 )− 3.
4
18.(12分)
已知函数h ( x )=log x(a >0且a≠1),h ( 72 )−3h ( 2 )=2.
a
2
h3x−
(1)求方程3 x =5的解集;
(2)求关于m的不等式h ( 4−m )>h ( 3m+2 )的解集.
19.(12分)
3π 3 3π
已知sin α+ = ,α∈ π, .
2 5 2
π
(1)求sin2α+ 的值;
4
α
(2)求tan 的值.
2
20.(12分)
已知函数 f ( x )=6sinaxcosax+2 3cos2ax− 3 ( a>0 )的最小正周期为π.
π
(1)将 f ( x )化简成 f ( x )= Asin (ωx+ϕ)+BA>0,ω>0,ϕ< 的形式;
3
x π 5π π 5π
(2)设函数g ( x )= f ,求函数h ( x )= gx− +g −x在 , 上的值域.
2 6 6 6 6
21.(12分)
已知某批药品在 2023 年治愈效果的普姆克系数 y(单位:pmk)与月份x ( 1≤ x≤12,x∈N )的部分统计数据
如下表:
x/月 10 11 12
普姆克系数y/pm 10240 20480 40960
(1)根据上表数据,从下列两个函数模型①y =max( m>0,a>1 ),②y =n x +m ( n>0,m>0 )中选取一
个恰当的函数模型描述该批药品在2023年治愈效果的普姆克系数y与月份x之间的关系,并写出这个函数解
学科网(北京)股份有限公司析式;
(2)用(1)中的函数模型,试问哪几个月该批药品治愈效果的普姆克系数在(1000,10000)内?
22.(12分)
已知函数 f ( x )=23x +m⋅2−3x为偶函数.
(1)求m的值;
2x x
(2)若关于x的不等式 f ≥kf − 恒成立,求k的取值范围;
3 3
10 53
(3)若 f ( c )=8−c −c+4,证明: < f ( c )< .
3 14
学科网(北京)股份有限公司2023—2024 学年高一第二学期开学检测考试
数学参考答案
1.C由题意得N = { x x>−2 } ,则M N =(−2,4 ) .
2.A由 a ≥4,解得a≤−4或a≥4,则“a≥4”是“ a ≥4”的充分不必要条件.
7 3 π
3.A由题意得tanα= = 3,又因为角α的终边在第一象限,所以角α的值可能为 .
7 3
4.D因为0lg10=1,所以b0,
8.B 若 f ( x )在R 上单调递增,则m>1, 解得m≥2 .若 f ( x )在R 上单调递减,则
5m−3−2m2 +1≤log 1,
m
5m−3<0,
1 3 1 3
00 ,则不等式
ax2 −4x+2<0有解,当a >0时,由△=16−8a >0,解得00,
13. ( 4,+∞) 由 得x>4.
x−4>0,
m2 n2 m2 n2 mn mn m2 n2
14.10 因为 + =1≥2 × =2× = ,当且仅当 = ,即4m=5n=10 2时,等号
25 16 25 16 5×4 10 25 16
成立,所以mn≤10,故mn的最大值为10.
2π 4π 4π
15.6;18π设圆心角∠POQ=α,则α= = = ,解得OP=6分米,所以OM =12分米,则
OP OM OP+6
学科网(北京)股份有限公司1 1
此扇环形砖雕的面积为 ×4π×12− ×2π×6=18π平方分米.
2 2
2x+1−1 2x+1−1 −k⋅2y −1
16.-2 设 y =log ,则 2y = ,即 2x = ①,由 f ( f ( x )) = x 得 f ( y )= x ,则
2 2x +k 2x +k 2y −2
2y+1−1 −k⋅2y −1 2y+1−1
2x = ② , 由 ① ② 可 得 = , 即 ( k+2 )22y +( k−2 ) 2y +1 =0 , 因 为
2y +k 2y −2 2y +k
22y +( k−2 ) 2y +1不恒为0,所以k+2=0,所以k =−2,经验证,符合题意.
17.解:(1)原式=lg5+lg2−3log 3×log 2=lg10−3=1−3=−2
2 3
1 − 2
4 2 1 3 2 − 1 2 1 10
(2)原式= −1−272 = −1−27 3 = −1− =− .
81 9 9 3 9
18.解:(1)由h ( 72 )−3h ( 2 )=2,得log 72−3log 2=log 72−log 8=log 9=2,
a a a a a
则a2 =9,解得a=3.
2 2
3
h
3x−
x
=3
log 3
3x−
x
=3x−
2
=5,
x
1
即3x2 −5x−2=0,解得x=2或− ,
3
2
h3x− 1
故方程3 x =5的解集为− ,2.
3
(2)因为h ( x )=log x是( 0,+∞)上的增函数,h ( 4−m )>h ( 3m+2 ),
3
4−m>0,
所以3m+2>0,
4−m>3m+2,
2 1 2 1
解得− h ( 3m+2 )的解集为 − , .
3 2 3 2
3π
sin (α−π) cos
2
−α
−sinα⋅(−sinα)
19.解:(1) f (α)= = =−tan2α,
π cosα⋅(−cosα)
sin −α cos (π+α)
2
35π 35π 5π 1
则 f =−tan2 =−tan2 =− .
6 6 6 3
学科网(北京)股份有限公司(2)由(1)知tan2θ=4,
3π
因为θ∈ π, ,所以tanθ=2.
2
方法一:
6sin2θ−5sinθcosθ
6sin2θ−5sinθcosθ=
sin2θ+cos2θ
6sin2θ−5sinθcosθ
cos2θ 6tan2θ−5tanθ 14
= = =
sin2θ+cos2θ tan2θ+1 5
cos2θ
方法二:
2 5
sinθ=− ,
5
5
cosθ=− ,
5
2
2 5 2 5 5 14
6sin2θ−5sinθcosθ=6×− −5×− ×− = .
5 5 5 5
20.解:(1)令ex +e=t,得x=ln ( t−e ),t >e,
因为 f ( ex +e ) = x+1,所以 f ( t )=ln ( t−e )+1,
所以 f ( x )=ln ( x−e )+1,x∈( e,+∞) .
(2)由题意得g ( x )=ln ( lnx )+lnx+2.
令lnx=a,由x∈
e,ee
,得a=lnx∈[ 1,e ],
g
(
x
)=h (
a
)=lna+a+2,
易得h ( a )在[ 1,e ]上单调递增,所以h ( 1 )≤h ( a )≤h ( e ),
h
(
1
)=ln1+1+2=3,
h
(
e
)=lne+e+2=3+e,
故g ( x )在 e,ee 上的值域为[ 3,3+e ] .
21.解:(1)因为函数模型①是指数型函数,其增长速度较快,函数模型②的增长速度较为缓慢,所以根据表中
学科网(北京)股份有限公司数据,应选函数模型①更为恰当.
根据题意可得x=11时,y =20480;当x=12时,y =40960.
ma11 =20480, m=10,
由 解得
ma12 =40960, a=2.
故该函数模型的解析式为y =10×2x( 1≤ x≤12,x∈N ) .
(2)函数y =10×2x在其定义域内单调递增.
令1000<10×2x <10000,
得log 100< x0,
3 3
22x +2−2x ( 2x +2−x )2 −2 2
所以k ≤ = =2x +2−x − ,
2x +2−x 2x +2−x 2x +2−x
令t =2x +2−x ≥2 2x⋅2−x =2,当且仅当x=0时,等号成立,
2
因为函数g ( t )=t− 在[ 2,+∞)上单调递增,
t
所以g ( t )≥ g ( 2 )=2−1=1,
所以k ≤1,即k的取值范围为(−∞,1 ] .
(3)证明:由 f ( c )=8−c −c+4,得8c +8−c =8−c −c+4,即8c +c−4=0,
设函数ϕ(
x
)=8x +x−4,则ϕ(
x
)在R上单调递增,
因为ϕ( log 3 )=3+log 3−4<0,
8 8
ϕ( log 3.5 )=3.5+log 3.5−4=log 3.5−0.5>log 2 2−0.5=0,
8 8 8 8
所以00,所以 f ( x )− f ( x )<0,即 f ( x )< f ( x ),
1 2 1 2
所以 f ( x )在( 0,+∞)上单调递增,则 f ( log 3 )< f ( c )< f ( log 3.5 ),
8 8
1 10
因为 f ( log 3 )=23log 8 3+2−3log 8 3 =8log 8 3+8−log 8 3 =3+ = ,
8 3 3
7 2 53
f ( log 3.5 )=23log 8 3.5 +2−3log 8 3.5 =8log 3 3.5 +8−log 9 3.5 = + = ,
8 2 7 14
10 53
即 < f ( c )< .
3 14
学科网(北京)股份有限公司