宝鸡中学2022级高三第一学期月考三考试试题-数学_2024-2025高三（6-6月题库）_2024年12月试卷_1203陕西省宝鸡市宝鸡中学2024-2025学年高三上学期12月月考

宝鸡中学 2022 级高三月考三考试试题 数学 本试卷共四大题，19小题；考试时长 120分钟，卷面满分 150分。 注意事项： 1.答卷前，考生务必将自己的姓名、班级、考场/座位号填写在答题卡上，将条形码准 确粘贴在条形码粘贴处。 2.回答选择题时，选出每小题答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑； 如需改动，用橡皮擦干净后，再选涂其它答案标号。涂写在本试卷上无效。 3.作答非选择题时，将答案书写在答题卡上，书写在本试卷上无效。 4.考试结束后，将答题卡交回。 一、单项选择题：本大题共 8 小题，每小题 5 分，共 40 分. 在每小题给出的四个选项 中，只有一个选项是正确的．请把正确的选项填涂在答题卡相应的位置上. 1.已知集合A{0,1,2,3,6}，B{x|x1A}，则ð (AB)( ) A A. {1,5} B. {3,6} C. {0,1,2} D. {0,6} 2.已知复数z满足(1i)z| 3i|，i为虚数单位，则z等于( ) 1 1 1 1 A. 1i B. 1i C.  i D.  i 2 2 2 2 1 1 3.( )m ( )n是log mlog n的( ) 2 2 2 2 A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件          4.设a，b 均为非零向量，且a (a b)，|b |2|a|，则a与b 的夹角为( )    2 A. B. C. D. 6 4 3 3 y2 5.已知双曲线x2  1(b0)的一条渐近线方程为 y  3x ，则b( ) b2 1 3 A. B. C. 3 D.3 3 3 第 页，共 页 1 5 {#{QQABLYQEggiIABAAAAgCAw0iCkAQkgGCAYgOBEAIMAAASQNABAA=}#}6.下列函数的图象不可能与直线 y  2xm，mR相切的是( ) x2 A. f(x) x2  x B. f(x)x3 ex C. f(x)lnx D. f(x) x 2x 2 7.将边长为2的正方形ABCD沿对角线AC折起，折起后点D记为D.若BD 2，则四面 体 ABCD的体积为( ) 2 2 2 A. B. C. 2 2 D. 2 3 3 3 8.已知 f(x)是定义域为R的偶函数，当x 0时， f(x)(xa)(x )2，若 f(x)有且仅有3 2 1 个零点，则关于x的不等式 f(x) f( )的解集为( ) 2 5 5 A. (,2)(2,) B. (, )( ,) 2 2 C. (,3)(3,) D. (,4)(4,) 二、多项选择题：本大题共 3 小题，每小题 6 分，共 18 分. 在每小题给出的四个选项 中，有多项符合题目要求. 全部选对得 6 分，选对但不全的得部分分，有选错的得 0 分. 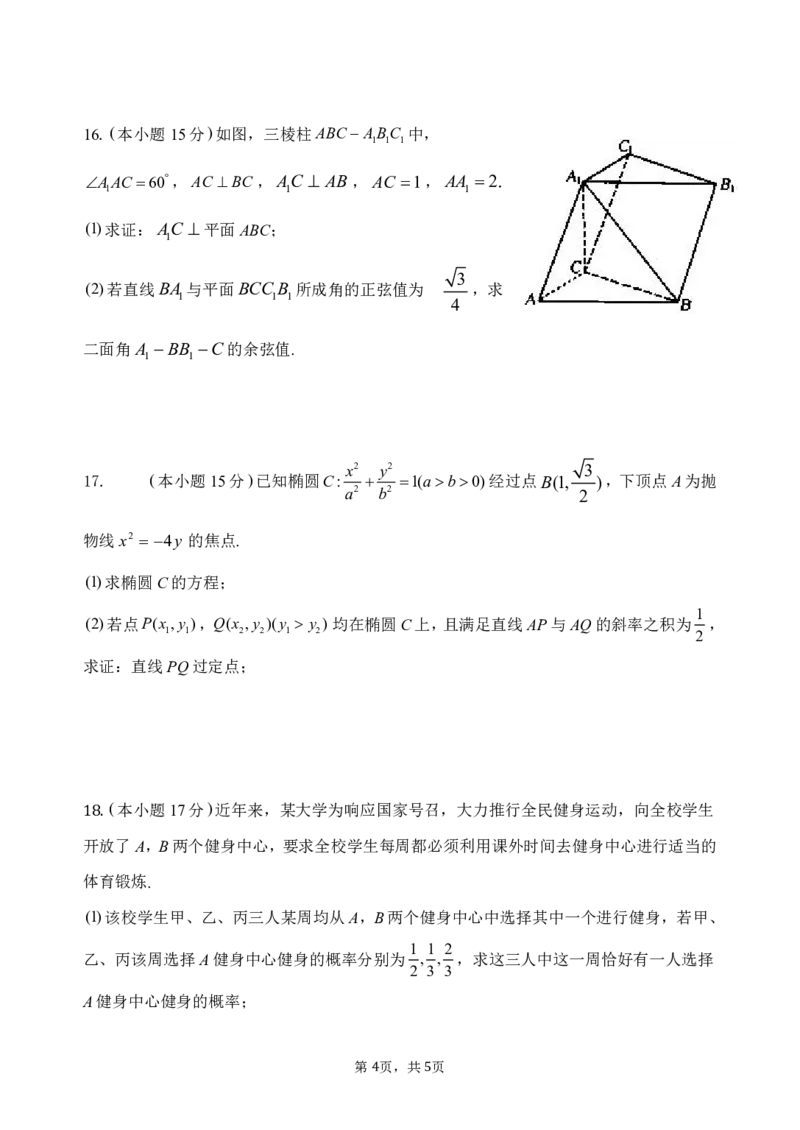9.已知 f (x)  Asin(x)(A 0, 0,0)是某个简谐运 动的函数解析式，其部分图象如图所示，则下列命题正确的是( ) A. 2  5 B.这个简谐运动的初相为 或 6 6 5 C. f(x)在[ ,3]上单调递减 2  D.将函数 f(x)的图象向左平移 个单位长度得到的图象对应的函数是偶函数 6 10.设函数 f(x)x3 x2 ax1，则( ) A.当a  1时， f(x)的极大值大于0 1 B.当a 时， f(x)无极值点 3 第 页，共 页 2 5 {#{QQABLYQEggiIABAAAAgCAw0iCkAQkgGCAYgOBEAIMAAASQNABAA=}#}C. aR，使 f(x)在R上是减函数 D. aR ，曲线y f(x)的对称中心的横坐标为定值 11.已知等比数列{a }的首项a 0，公比为q(q 1)，前n项和为S ，前n项积为T ，则 n 1 n n ( ) A.若数列{S }是递增数列，则q 1 n B.若数列{T }是递增数列，则q 1 n C.当0q1时，存在实数M，使得S M 恒成立 n D.若T T T ，则使得T 1成立的n的最大值为10 5 6 4 n 三、填空题：本大题共 3 小题，每小题 5 分，共 15 分. 1cos sin 12.已知  4，则tan______. sin 1cos 2n a 13.已知正项数列{a }满足a  a ，则 10 ______. n n1 n1 n a 6 14.在坐标平面内，横、纵坐标均为整数的点称为整点．点P从原点出发，在坐标平面内跳 跃行进，每次跳跃的长度都是5且落在整点处．则点P到达点Q(33,33)所跳跃次数的最小 值是______. 四、解答题：本题共 5 小题，共 77 分. 解答应写出文字说明、证明过程或演算步骤. 15.(本小题13分)若锐角ABC 的内角A，B，C所对的边分别为a，b，c，其外接圆的半 径为 3，且acos(BC)acosA2 3csinBcosA. (1)求角A的大小； b2 a2 (2)求 的取值范围. 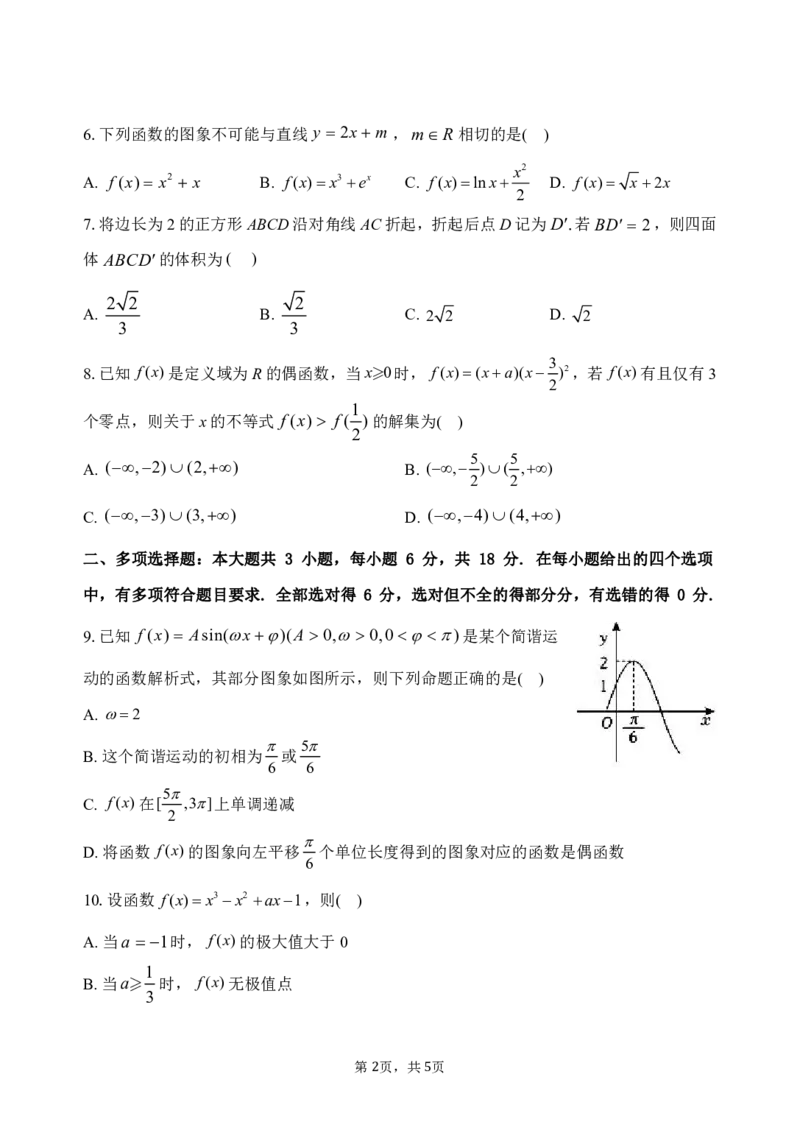b 第 页，共 页 3 5 {#{QQABLYQEggiIABAAAAgCAw0iCkAQkgGCAYgOBEAIMAAASQNABAA=}#}16.(本小题15分)如图，三棱柱ABC ABC 中， 1 1 1 AAC60，AC BC，AC  AB ， AC 1， AA 2. 1 1 1 (1)求证：AC 平面ABC； 1 3 (2)若直线BA 与平面BCC B 所成角的正弦值为 ，求 1 1 1 4 二面角 A BB C的余弦值. 1 1 x2 y2 3 17. (本小题15分)已知椭圆C:  1(ab0)经过点B(1, )，下顶点A为抛 a2 b2 2 物线x2  4y 的焦点. (1)求椭圆C的方程； 1 (2)若点P(x,y )，Q(x ,y )(y  y )均在椭圆C上，且满足直线AP与AQ的斜率之积为 ， 1 1 2 2 1 2 2 求证：直线PQ过定点； (本小题17分)近年来，某大学为响应国家号召，大力推行全民健身运动，向全校学生 1开8放. 了A，B两个健身中心，要求全校学生每周都必须利用课外时间去健身中心进行适当的 体育锻炼. (1)该校学生甲、乙、丙三人某周均从A，B两个健身中心中选择其中一个进行健身，若甲、 1 1 2 乙、丙该周选择A健身中心健身的概率分别为 , , ，求这三人中这一周恰好有一人选择 2 3 3 A健身中心健身的概率； 第 页，共 页 4 5 {#{QQABLYQEggiIABAAAAgCAw0iCkAQkgGCAYgOBEAIMAAASQNABAA=}#}(2)该校学生丁每周六、日均去健身中心进行体育锻炼，且这两天中每天只选择两个健身中 1 心的其中一个，其中周六选择A健身中心的概率为 .若丁周六选择A健身中心，则周日仍 2 1 2 选择A健身中心的概率为 ；若周六选择B健身中心，则周日选择A健身中心的概率为 . 4 3 求丁周日选择B健身中心健身的概率； (3)现用健身指数k(k[0,10])来衡量各学生在一个月的健身运动后的健身效果，并规定k 值低于1分的学生为健身效果不佳的学生，经统计发现从全校学生中随机抽取一人，其k 值低于1分的概率为0.02.现从全校学生中随机抽取一人，如果抽取到的学生不是健身效果 不佳的学生，则继续抽取下一个，直至抽取到一位健身效果不佳的学生为止，但抽取的总 次数不超过n.若抽取次数的期望值不超过23，求n的最大值. 参考数据：0.9829 0.557，0.9830 0.545，0.9831 0.535. 19.(本小题17分)已知函数 f(x)axlog x(a0,且a 1). a (1)当ae时，证明： f(x)为增函数； (2)若 f(x)存在两个极值点x ，x . 1 2 (i)求a的取值范围； (ii)设 f(x)的极大值为M，求M的取值范围. 第 页，共 页 5 5 {#{QQABLYQEggiIABAAAAgCAw0iCkAQkgGCAYgOBEAIMAAASQNABAA=}#}