文档内容
2003 年新疆高考文科数学真题及答案
一、选择题(共12小题,每小题5分,满分60分)
1.(5分)直线y=2x关于x轴对称的直线方程为( )
A. B. C.y=﹣2x D.y=2x
2.(5分)已知x∈( ,0),cosx ,则tan2x等于( )
A. B. C. D.
3.(5分)抛物线y=ax2的准线方程是y=2,则a的值为( )
A. B. C.8 D.﹣8
4.(5分)等差数列{a}中,已知a ,a+a=4,a=33,则n为( )
n 1 2 5 n
A.48 B.49 C.50 D.51
5.(5分)双曲线虚轴的一个端点为M,两个焦点为F、F,∠FMF=120°,则双曲线的离
1 2 1 2
心率为( )
A. B. C. D.
6.(5分)设函数 若f(x)>1,则x的取值范围是( )
0 0
A.(﹣1,1) B.(﹣1,+∞)
C.(﹣∞,﹣2)∪(0,+∞) D.(﹣∞,﹣1)∪(1,+∞)
7.(5分)已知f(x5)=lgx,则f(2)=( )
A.lg2 B.lg32 C. D.
8.(5分)函数y=sin(x+φ)(0≤φ≤π)是R上的偶函数,则φ=( )
A.0 B. C. D.π
第1页 | 共16页9.(5分)已知点(a,2)(a>0)到直线l:x﹣y+3=0的距离为1,则a=( )
A. B. C. D.
10.(5分)已知圆锥的底面半径为R,高为3R,它的内接圆柱的底面半径为 ,该圆柱的
全面积为( )
A.2πR2 B. C. D.
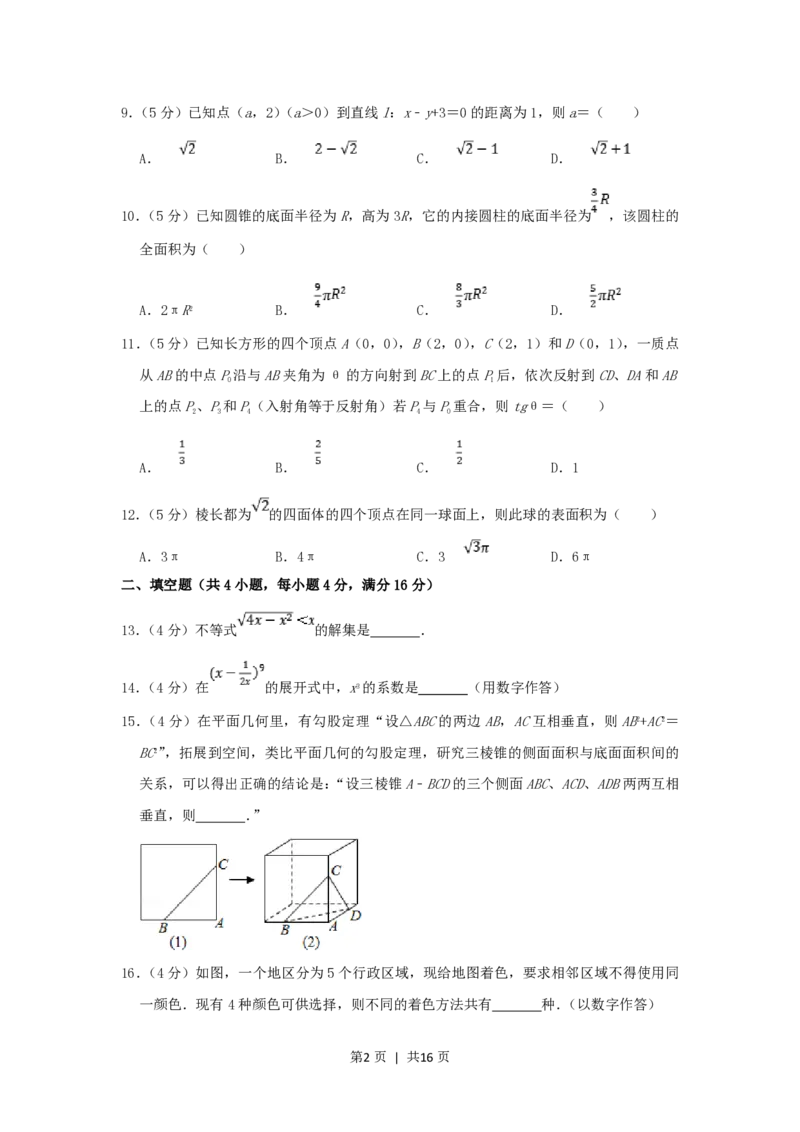
11.(5分)已知长方形的四个顶点A(0,0),B(2,0),C(2,1)和D(0,1),一质点
从AB的中点P沿与AB夹角为θ的方向射到BC上的点P后,依次反射到CD、DA和AB
0 1
上的点P、P和P(入射角等于反射角)若P与P重合,则tgθ=( )
2 3 4 4 0
A. B. C. D.1
12.(5分)棱长都为 的四面体的四个顶点在同一球面上,则此球的表面积为( )
A.3π B.4π C.3 D.6π
二、填空题(共4小题,每小题4分,满分16分)
13.(4分)不等式 的解集是 .
14.(4分)在 的展开式中,x3的系数是 (用数字作答)
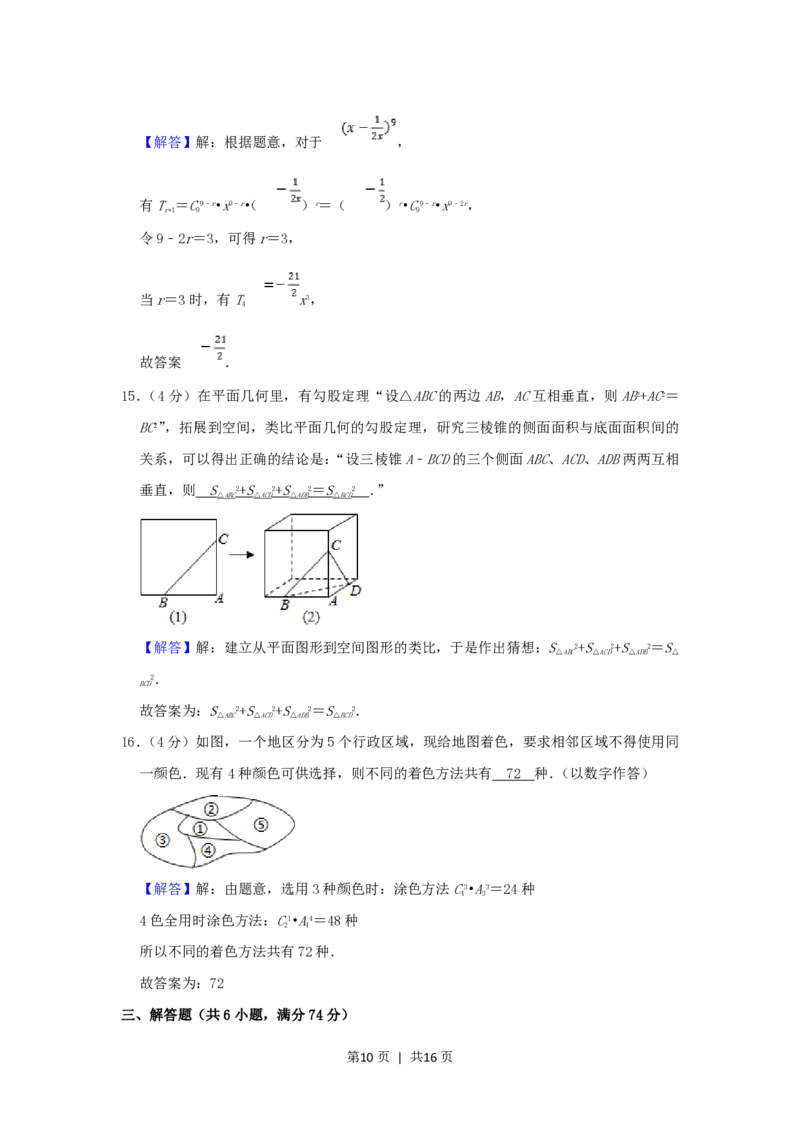
15.(4分)在平面几何里,有勾股定理“设△ABC的两边AB,AC互相垂直,则AB2+AC2=
BC2”,拓展到空间,类比平面几何的勾股定理,研究三棱锥的侧面面积与底面面积间的
关系,可以得出正确的结论是:“设三棱锥A﹣BCD的三个侧面ABC、ACD、ADB两两互相
垂直,则 .”
16.(4分)如图,一个地区分为5个行政区域,现给地图着色,要求相邻区域不得使用同
一颜色.现有4种颜色可供选择,则不同的着色方法共有 种.(以数字作答)
第2页 | 共16页三、解答题(共6小题,满分74分)
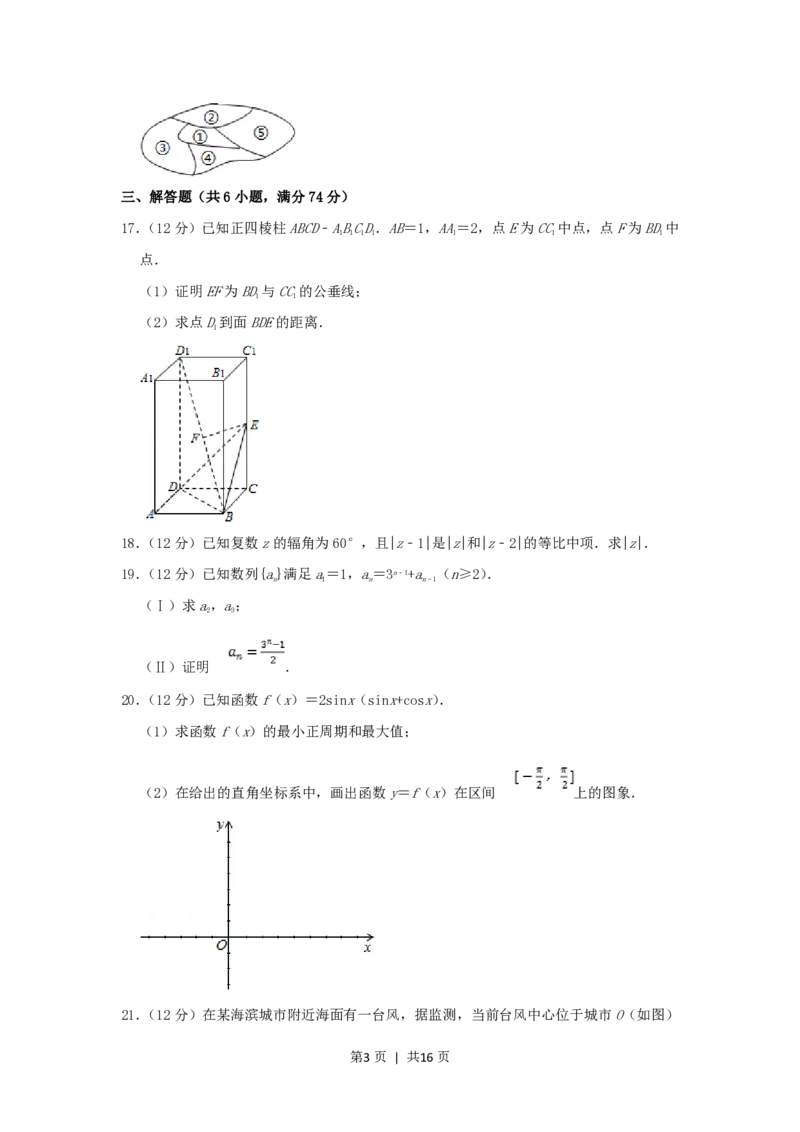
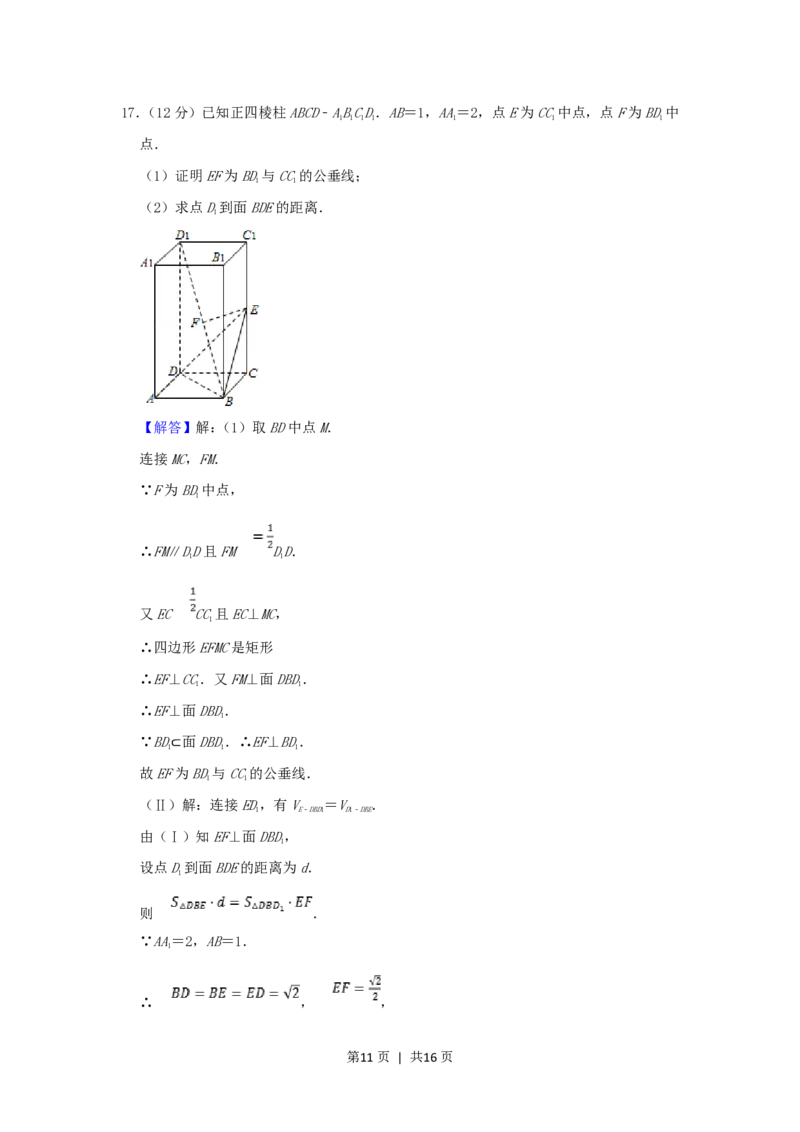
17.(12分)已知正四棱柱ABCD﹣ABCD.AB=1,AA=2,点E为CC中点,点F为BD中
1 1 1 1 1 1 1
点.
(1)证明EF为BD与CC的公垂线;
1 1
(2)求点D到面BDE的距离.
1
18.(12分)已知复数z的辐角为60°,且|z﹣1|是|z|和|z﹣2|的等比中项.求|z|.
19.(12分)已知数列{a}满足a=1,a=3n﹣1+a (n≥2).
n 1 n n﹣1
(Ⅰ)求a,a;
2 3
(Ⅱ)证明 .
20.(12分)已知函数f(x)=2sinx(sinx+cosx).
(1)求函数f(x)的最小正周期和最大值;
(2)在给出的直角坐标系中,画出函数y=f(x)在区间 上的图象.
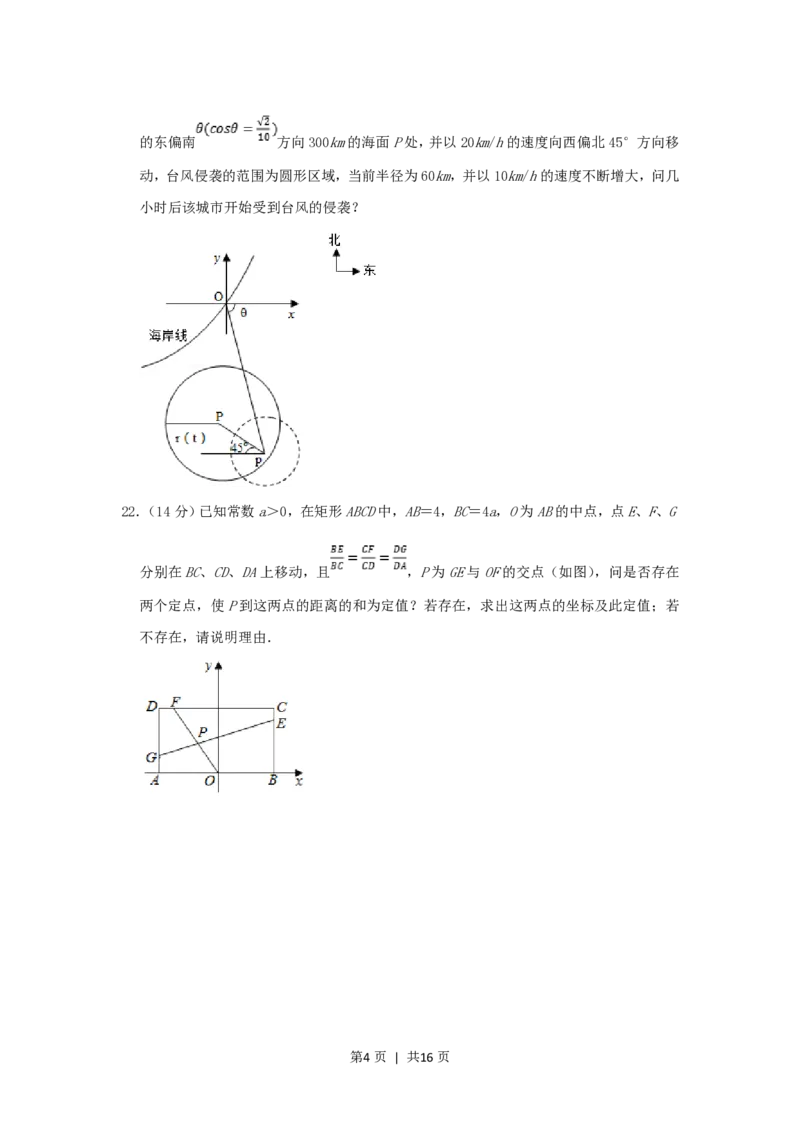
21.(12分)在某海滨城市附近海面有一台风,据监测,当前台风中心位于城市O(如图)
第3页 | 共16页的东偏南 方向300km的海面P处,并以20km/h的速度向西偏北45°方向移
动,台风侵袭的范围为圆形区域,当前半径为60km,并以10km/h的速度不断增大,问几
小时后该城市开始受到台风的侵袭?
22.(14分)已知常数a>0,在矩形ABCD中,AB=4,BC=4a,O为AB的中点,点E、F、G
分别在BC、CD、DA上移动,且 ,P为GE与OF的交点(如图),问是否存在
两个定点,使P到这两点的距离的和为定值?若存在,求出这两点的坐标及此定值;若
不存在,请说明理由.
第4页 | 共16页2003年全国统一高考数学试卷(文科)
参考答案与试题解析
一、选择题(共12小题,每小题5分,满分60分)
1.(5分)直线y=2x关于x轴对称的直线方程为( )
A. B. C.y=﹣2x D.y=2x
【解答】解:∵直线y=f(x)关于x对称的直线方程为y=﹣f(x),
∴直线y=2x关于x对称的直线方程为:
y=﹣2x.
故选:C.
2.(5分)已知x∈( ,0),cosx ,则tan2x等于( )
A. B. C. D.
【解答】解:∵cosx ,x∈( ,0),
∴sinx .∴tanx .
∴tan2x .
故选:D.
3.(5分)抛物线y=ax2的准线方程是y=2,则a的值为( )
A. B. C.8 D.﹣8
【解答】解:抛物线y=ax2的标准方程是x2 y,
则其准线方程为y 2,
第5页 | 共16页所以a .
故选:B.
4.(5分)等差数列{a}中,已知a ,a+a=4,a=33,则n为( )
n 1 2 5 n
A.48 B.49 C.50 D.51
【解答】解:设{a}的公差为d,
n
∵ ,a+a=4,
2 5
∴ d 4d=4,即 5d=4,
解得d .
∴an (n﹣1) ,
令a=33,
n
即 33,
解得n=50.
故选:C.
5.(5分)双曲线虚轴的一个端点为M,两个焦点为F、F,∠FMF=120°,则双曲线的离
1 2 1 2
心率为( )
A. B. C. D.
【解答】解:根据双曲线对称性可知∠OMF=60°,
2
∴tan∠OMF ,即c b,
2
∴a b,
第6页 | 共16页∴e .
故选:B.
6.(5分)设函数 若f(x)>1,则x的取值范围是( )
0 0
A.(﹣1,1) B.(﹣1,+∞)
C.(﹣∞,﹣2)∪(0,+∞) D.(﹣∞,﹣1)∪(1,+∞)
【解答】解:当x≤0时, ,则x<﹣1,
0 0
当x>0时, 则x>1,
0 0
故x的取值范围是(﹣∞,﹣1)∪(1,+∞),
0
故选:D.
7.(5分)已知f(x5)=lgx,则f(2)=( )
A.lg2 B.lg32 C. D.
【解答】解:令x5=2,
∴得x ,
∵f(x5)=lgx,
∴f(2)=lg lg2.
故选:D.
8.(5分)函数y=sin(x+φ)(0≤φ≤π)是R上的偶函数,则φ=( )
A.0 B. C. D.π
【解答】解:当φ=0时,y=sin(x+φ)=sinx为奇函数不满足题意,排除A;
当φ 时,y=sin(x+φ)=sin(x )为非奇非偶函数,排除B;
第7页 | 共16页当φ 时,y=sin(x+φ)=cosx,为偶函数,满足条件.
当φ=π时,y=sin(x+φ)=﹣sinx,为奇函数,
故选:C.
9.(5分)已知点(a,2)(a>0)到直线l:x﹣y+3=0的距离为1,则a=( )
A. B. C. D.
【解答】解:由点到直线的距离公式得: ,
∵a>0,
∴a .
故选:C.
10.(5分)已知圆锥的底面半径为R,高为3R,它的内接圆柱的底面半径为 ,该圆柱的
全面积为( )
A.2πR2 B. C. D.
【解答】解:设圆锥内接圆柱的高为h,则 ,解得 ,
所以圆柱的全面积为:s=2 .
故选:B.
11.(5分)已知长方形的四个顶点A(0,0),B(2,0),C(2,1)和D(0,1),一质点
从AB的中点P沿与AB夹角为θ的方向射到BC上的点P后,依次反射到CD、DA和AB
0 1
上的点P、P和P(入射角等于反射角)若P与P重合,则tgθ=( )
2 3 4 4 0
A. B. C. D.1
【解答】解:由于若P与P重合,
4 0
故P、P也都是所在边的中点,
2 3
因为ABCD是长方形,
第8页 | 共16页根据对称性可知PP的斜率是 ,
0 1
则tgθ .
故选:C.
12.(5分)棱长都为 的四面体的四个顶点在同一球面上,则此球的表面积为( )
A.3π B.4π C.3 D.6π
【解答】解:借助立体几何的两个熟知的结论:
(1)一个正方体可以内接一个正四面体;
(2)若正方体的顶点都在一个球面上,则正方体的体对角线就是球的直径.
则球的半径R ,
∴球的表面积为3π,
故选:A.
二、填空题(共4小题,每小题4分,满分16分)
13.(4分)不等式 的解集是 (2,4] .
【解答】解:∵x 0,
∴x>0,
∵不等式 ,两边平方得,
4x﹣x2<x2,
∴2x2﹣4x>0,
解得,x>2,x<0(舍去),
∵4x﹣x2≥0,
∴0≤x≤4,
∴综上得:不等式的解集为:(2,4],
故答案为(2,4].
14.(4分)在 的展开式中,x3的系数是 (用数字作答)
第9页 | 共16页【解答】解:根据题意,对于 ,
有T =C9﹣r•x9﹣r•( )r=( )r•C9﹣r•x9﹣2r,
r+1 9 9
令9﹣2r=3,可得r=3,
当r=3时,有T x3,
4
故答案 .
15.(4分)在平面几何里,有勾股定理“设△ABC的两边AB,AC互相垂直,则AB2+AC2=
BC2”,拓展到空间,类比平面几何的勾股定理,研究三棱锥的侧面面积与底面面积间的
关系,可以得出正确的结论是:“设三棱锥A﹣BCD的三个侧面ABC、ACD、ADB两两互相
垂直,则 S 2+S 2+S 2=S 2 .”
△ABC △ACD △ADB △BCD
【解答】解:建立从平面图形到空间图形的类比,于是作出猜想:S 2+S 2+S 2=S
△ABC △ACD △ADB △
2.
BCD
故答案为:S 2+S 2+S 2=S 2.
△ABC △ACD △ADB △BCD
16.(4分)如图,一个地区分为5个行政区域,现给地图着色,要求相邻区域不得使用同
一颜色.现有4种颜色可供选择,则不同的着色方法共有 72 种.(以数字作答)
【解答】解:由题意,选用3种颜色时:涂色方法C3•A3=24种
4 3
4色全用时涂色方法:C1•A4=48种
2 4
所以不同的着色方法共有72种.
故答案为:72
三、解答题(共6小题,满分74分)
第10页 | 共16页17.(12分)已知正四棱柱ABCD﹣ABCD.AB=1,AA=2,点E为CC中点,点F为BD中
1 1 1 1 1 1 1
点.
(1)证明EF为BD与CC的公垂线;
1 1
(2)求点D到面BDE的距离.
1
【解答】解:(1)取BD中点M.
连接MC,FM.
∵F为BD中点,
1
∴FM∥DD且FM DD.
1 1
又EC CC且EC⊥MC,
1
∴四边形EFMC是矩形
∴EF⊥CC.又FM⊥面DBD.
1 1
∴EF⊥面DBD.
1
∵BD⊂面DBD.∴EF⊥BD.
1 1 1
故EF为BD与CC的公垂线.
1 1
(Ⅱ)解:连接ED,有V =V .
1 E﹣DBD1 D1﹣DBE
由(Ⅰ)知EF⊥面DBD,
1
设点D到面BDE的距离为d.
1
则 .
∵AA=2,AB=1.
1
∴ , ,
第11页 | 共16页∴ .
∴
故点D到平面DBE的距离为 .
1
18.(12分)已知复数z的辐角为60°,且|z﹣1|是|z|和|z﹣2|的等比中项.求|z|.
【解答】解:设z=(rcos60°+rsin60°i),
则复数z的实部为 .
由题设|z﹣1|2=|z|•|z﹣2|,
即:(z﹣1)( 1)=|z|
∴r2﹣r+1=r ,
整理得r2+2r﹣1=0.
解得r 1,
r 1(舍去).
即|z| 1.
19.(12分)已知数列{a}满足a=1,a=3n﹣1+a (n≥2).
n 1 n n﹣1
(Ⅰ)求a,a;
2 3
(Ⅱ)证明 .
第12页 | 共16页【解答】解:(Ⅰ)∵a=1,
1
∴a=3+1=4,
2
∴a=32+4=13;
3
(Ⅱ)证明:由已知a﹣a =3n﹣1,n≥2
n n﹣1
故a=(a﹣a )+(a ﹣a )+…+(a﹣a)+a
n n n﹣1 n﹣1 n﹣2 2 1 1
.n≥2
当n=1时,也满足上式.
所以 .
20.(12分)已知函数f(x)=2sinx(sinx+cosx).
(1)求函数f(x)的最小正周期和最大值;
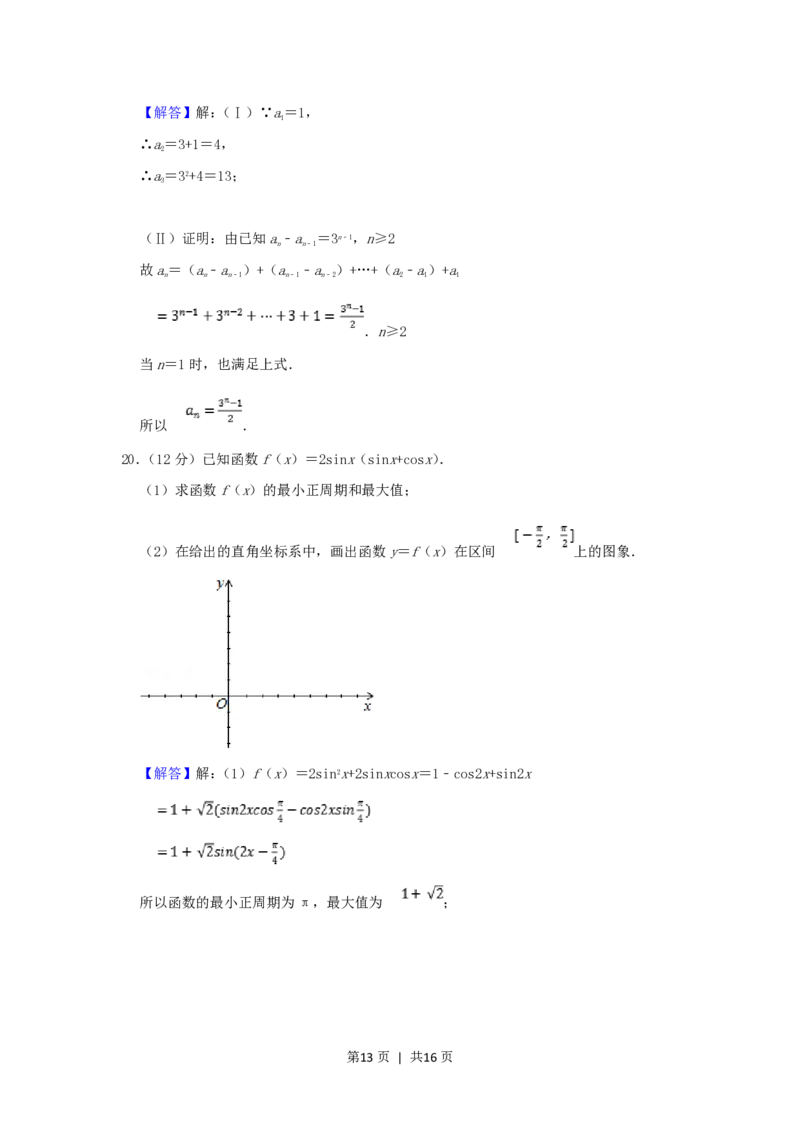
(2)在给出的直角坐标系中,画出函数y=f(x)在区间 上的图象.
【解答】解:(1)f(x)=2sin2x+2sinxcosx=1﹣cos2x+sin2x
所以函数的最小正周期为π,最大值为 ;
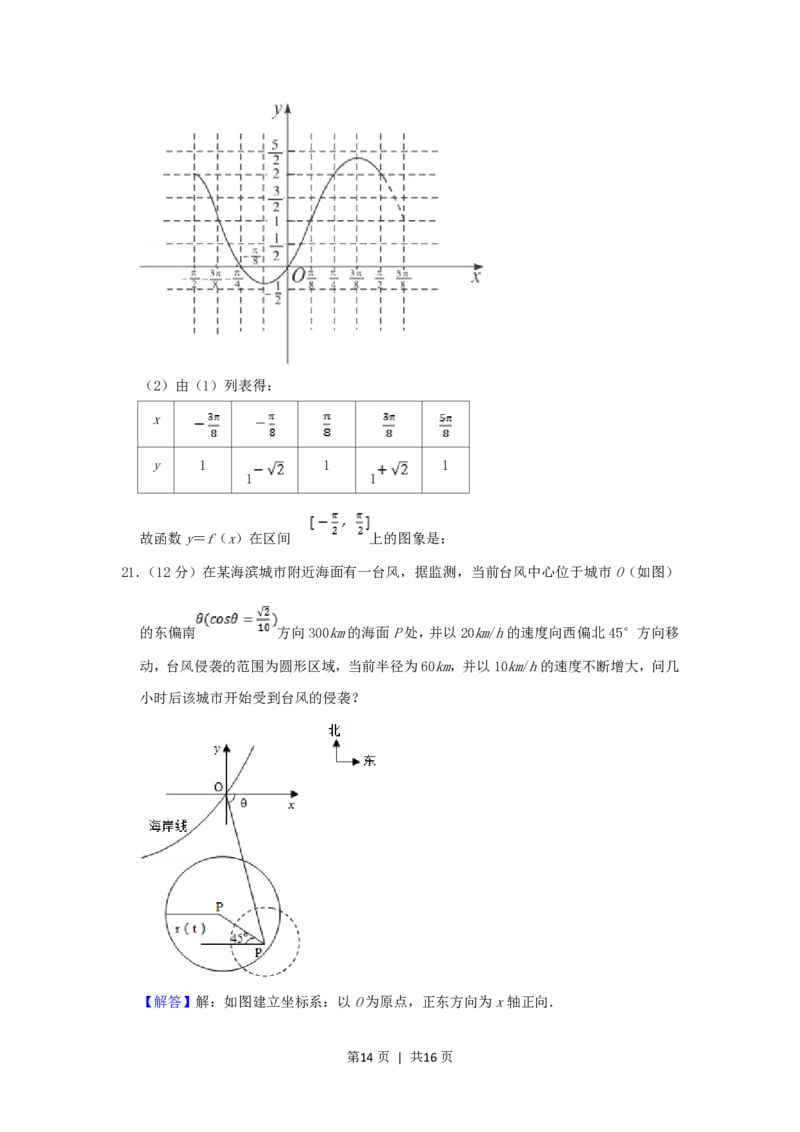
第13页 | 共16页(2)由(1)列表得:
x
y 1 1 1
1 1
故函数y=f(x)在区间 上的图象是:
21.(12分)在某海滨城市附近海面有一台风,据监测,当前台风中心位于城市O(如图)
的东偏南 方向300km的海面P处,并以20km/h的速度向西偏北45°方向移
动,台风侵袭的范围为圆形区域,当前半径为60km,并以10km/h的速度不断增大,问几
小时后该城市开始受到台风的侵袭?
【解答】解:如图建立坐标系:以O为原点,正东方向为x轴正向.
第14页 | 共16页在时刻:t(h)台风中心P(x,y)的坐标为
令(x′,y′)是台风边缘线上一点,则此时台风侵袭的区域是(x′﹣x)2+(y′﹣y)
2≤[r(t)]2,
其中r(t)=10t+60,
若在t时,该城市受到台风的侵袭,
则有(0﹣x)2+(0﹣y)2≤(10t+60)2,
即 ,
即t2﹣36t+288≤0,解得12≤t≤24.
答:12小时后该城市开始受到台风侵袭.
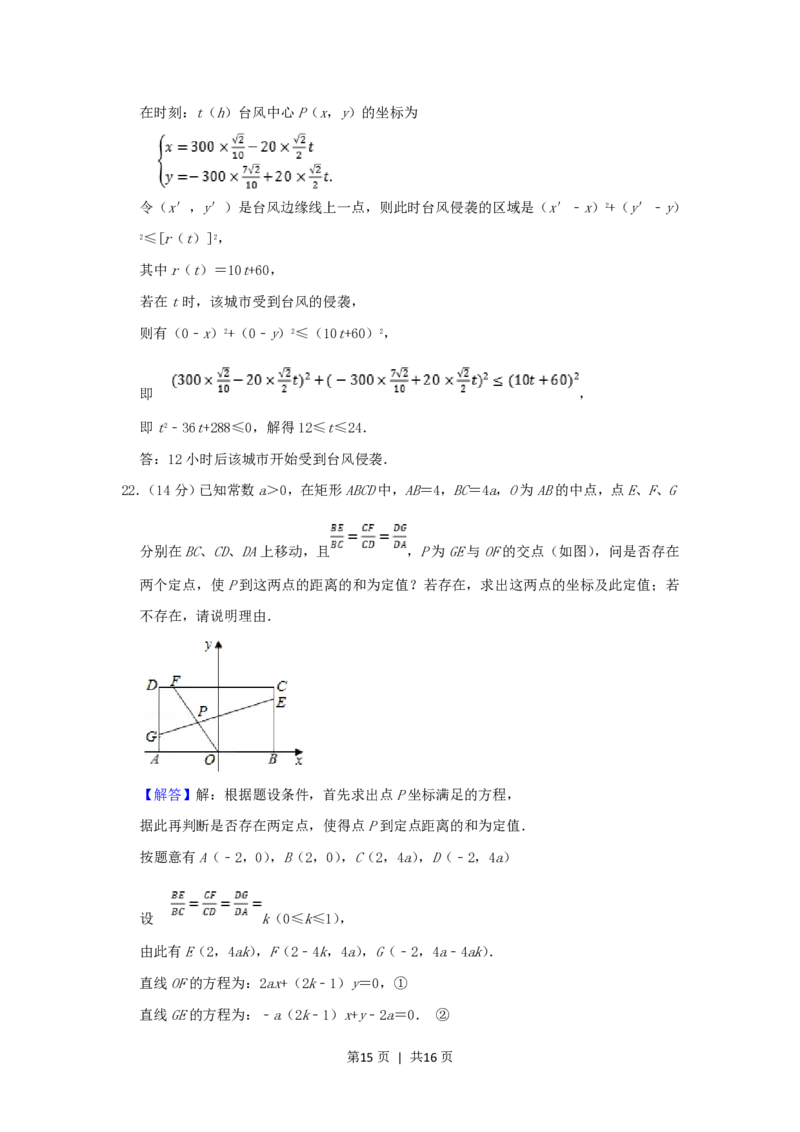
22.(14分)已知常数a>0,在矩形ABCD中,AB=4,BC=4a,O为AB的中点,点E、F、G
分别在BC、CD、DA上移动,且 ,P为GE与OF的交点(如图),问是否存在
两个定点,使P到这两点的距离的和为定值?若存在,求出这两点的坐标及此定值;若
不存在,请说明理由.
【解答】解:根据题设条件,首先求出点P坐标满足的方程,
据此再判断是否存在两定点,使得点P到定点距离的和为定值.
按题意有A(﹣2,0),B(2,0),C(2,4a),D(﹣2,4a)
设 k(0≤k≤1),
由此有E(2,4ak),F(2﹣4k,4a),G(﹣2,4a﹣4ak).
直线OF的方程为:2ax+(2k﹣1)y=0,①
直线GE的方程为:﹣a(2k﹣1)x+y﹣2a=0. ②
第15页 | 共16页从①,②消去参数k,
得点P(x,y)坐标满足方程2a2x2+y2﹣2ay=0,
整理得 .
当 时,点P的轨迹为圆弧,所以不存在符合题意的两点;
当 时,点P轨迹为椭圆的一部分,点P到该椭圆焦点的距离的和为定长;
当 时,点P到椭圆两个焦点 的距离之和为定值
;
当 时,点P到椭圆两个焦点 的距离之和
为定值2a.
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布
日期:2019/8/13 16:20:20;用户:黄熠;邮箱:huangyi12388@163.com;学号:716378
第16页 | 共16页