文档内容
2024-2025 学年度春学期期中联考试卷
高二数学
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目
要求的。
1. 下列求导数运算正确的是( )
1
A.(2x)′=2x B.(log x)'=
2 x
C.(e2x)′=2e2x D.(cosx)′=sinx
2. 某书架的第一层放有7本不同的历史书,第二层放有6本不同的地理书.从这些书中任取1本历史书
和1本地理书,不同的取法有( )
A.13种 B.42种 C.67种 D.7种
3. 已知f(x)=x2(x﹣k)的一个极值点为2,则实数k=( )
A.2 B.3 C.4 D.5
4. 某射手射击时击中目标的概率为0.7,设4次射击击中目标的次数为随机变量 ,则P( ≥1)等于(
)
ξ ξ
A.0.9163 B.0.0081 C.0.0756 D.0.9919
2025
5. 若(2x﹣1)2025=a +a x+a x2+…+a x2024+a x2025,则∑ a =( )
0 1 2 2024 2025 i
i=1
A. 2 B.﹣1 C.1 D.﹣2
6. 如图所示的一圆形花圃,拟在A,B,C,D区域种植花苗,现有3种不同颜色的花
苗,每个区域种植1种颜色的花苗,且相邻的2块区域种植颜色不同的花苗,则不同
的种植方法总数为( )
A.12 B.18 C.24 D.30
7. 若直线y=ex+a与曲线y=lnx+b相切,则a2+b2的最小值为( )
1
A.4 B.1 C. D.2
2
8. 已知函数f(x)的定义域为(﹣∞,+∞),f′(x)为f(x)的导函数,函数y
=f′(x)的图象如图所示,且f(﹣2)=1,f(3)=1,则不等式f(x2﹣6)
>1的解集为( )
A.(2,3) B.(-√2,√2)
C.(2,3)∪(﹣3,﹣2) D.(﹣∞,-√2)∪(√2,
+∞)二、选择题:本题共3小题,每小题6分,共18分。在每小题给出的选项中,有多项符合要求。全部选
对的得6分,部分选对的得部分分,有选错的得0分。
9. (多选)下列说法正确的是( )
A.用简单随机抽样的方法从含有50个个体的总体中抽取一个容量为5的样本,则个体m被抽到的概
率是0.1
B.数据5,8,10,12,13的第40百分位数是8
C.已知数据x
1
,x
2
,⋯,x
10
的极差为6,方差为2,则数据2x
1
+1,2x
2
+1,⋯,2x
10
+1的极差和方差
分别为12,8
D.若随机变量X服从正态分布N( ,σ2),P(X<﹣2)=P(X>4)=0.14,则P(1<X<4)=
0.36
μ
10. (多选)下列说法正确的是( )
A.随机变量 表示重复抛掷一枚骰子n次中出现点数是3的倍数的次数,则随机变量 服从二项分布.
B.有一批产品共有N件,其中M件为次品,采用有放回抽取方法, 表示n次抽取中出现次品的件数
ξ ξ
(M<N) ,则随机变量 服从二项分布.
ξ
C.有一批种子的发芽率为70%,任取10颗种子做发芽试验,把试验中发芽的种子的个数记为X,则
ξ
随机变量X服从超几何分布.
D.某班级有男生25人,女生20人,选派4名学生参加学校组织的活动,其中女生人数记为X,则随
机变量X服从超几何分布.
11. (多选)已知函数f(x)为定义(﹣∞,0)∪(0,+∞)上的奇函数,若当x<0时,xf '(x)﹣f
(x)<0,且f(1)=0,则( )
A.2f(e)>ef(2)
B.当m<2时,f(m)>mf(1)
C.3f(﹣ )+ f(3)<0
D.不等式f(x)>0解集为(﹣1,0)∪(1,+∞)
π π
三、填空题:本题共3小题,每小题5分,共15分。
12. 5555被8整除的余数为______.
13. 现有一质地均匀的正方体骰子(六个面分别标着数字1~6),连续投掷两次,记m,n分别为第一次、
第二次投掷后朝上的点数,设离散型随机变量X=|m﹣n|, 则P(X=1)的值为________.
14. 设h′(x)为h(x)的导函数,若h′(x)在区间D上单调递减,则称h(x)为D上的“凸函数”.
π
已知函数f(x)=﹣sinx+ax2+ax.若f(x)为[0, ]上的“凸函数”,则实数a的取值范围是
2
四、解答题:本题共5小题,共77分。解答应写出文字说明、证明过程或演算步骤。
15. (13分)已知函数f(x)=x3+ax2+bx(a R,b R),其图象在点(1,4)处的切线方程为y=4.
(1)求函数f(x)的解析式;
∈ ∈
(2)求函数f(x)在区间[0,5]上的最值.1
16. (15分)在(2√x- ) 6 的展开式中,求:
√x
(1)求常数项、及此项的二项式系数;
(2)求奇数项的二项式系数的和;
(3)求系数绝对值最大的项.
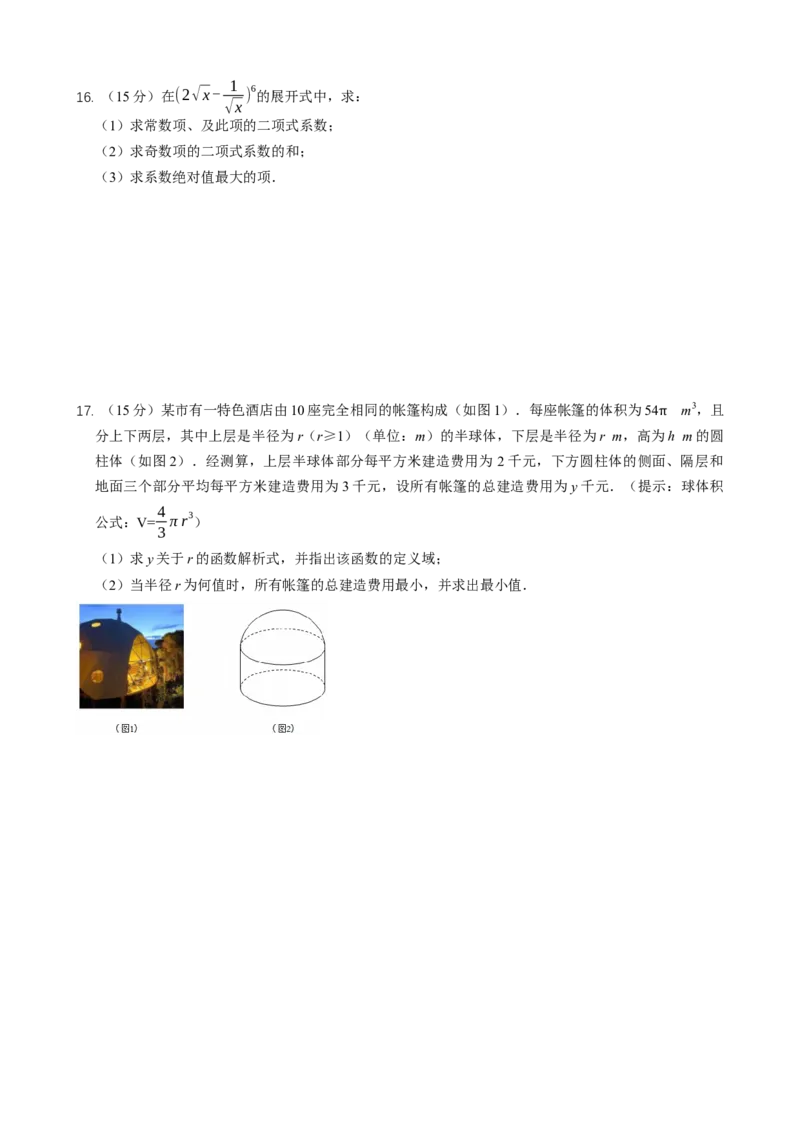
17. (15分)某市有一特色酒店由10座完全相同的帐篷构成(如图1).每座帐篷的体积为54 m3,且
分上下两层,其中上层是半径为r(r≥1)(单位:m)的半球体,下层是半径为r m,高为h m的圆
π
柱体(如图2).经测算,上层半球体部分每平方米建造费用为 2千元,下方圆柱体的侧面、隔层和
地面三个部分平均每平方米建造费用为3千元,设所有帐篷的总建造费用为y千元.(提示:球体积
4
公式:V=
πr3
)
3
(1)求y关于r的函数解析式,并指出该函数的定义域;
(2)当半径r为何值时,所有帐篷的总建造费用最小,并求出最小值.2
18. (17分)甲、乙两位同学进行乒乓球比赛,经过大数据分析,每局比赛甲获胜的概率约为 ,乙获胜
3
1
的概率约为 .
3
(1)若比赛为三局两胜制,
(i)设比赛结束时比赛场次为X,求X的分布列与数学期望;
(ii)求乙最终获胜的概率;
(2)若比赛为五局三胜制,已知甲最终获胜了,求在此条件下进行了5局比赛的概率.
19. (17分)已知函数f(x)=ex﹣ax﹣1.
(1)当a=1时,求f(x)的单调区间与极值;
(2)讨论f(x)的单调性;
(3)当a=1时,设g(x)=f(x)﹣x2, 证明:g(x)在(0,+∞)上存在唯一的极小值点x
0,
3
且g(x )>- .(参考数据:e3≈20.09.)
0 42024-2025 学年度春学期期中联考试卷
高二数学(评分细则)
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 C B B D A B D C
二.多选题(共3小题)
题号 9 10 11
答案 ACD ABD ACD
三.填空题(共3小题)
题号 12 13 14
答案 7 5 1
(-∞,- ]
18 2
四.解答题(共5小题)
15.已知函数f(x)=x3+ax2+bx(a R,b R),其图象在点(1,4)处的切线方程为y=4.
(1)求函数f(x)的解析式;
∈ ∈
(2)求函数f(x)在区间[0,5]上的最值.
【解答】解:(1)由f(x)=x3+ax2+bx(a R,b R)可得:f′(x)=3x2+2ax+b,
所以f(x)在点(1,4)处切线的斜率为k=f′(1)=3+2a+b,
∈ ∈
因为f(x)在点(1,4)处切线方程为y=4,
所以切线的斜率为0,且f(1)=4,
{f '(1)=0 {3+2a+b=0
所以 ,即 ,…………………………………………………………4分(各2分)
f(1)=4 1+a+b=4
解得a=﹣6,b=9,
所以f(x)=x3﹣6x2+9x;……………………………………………………………………..6分
(2)由(1)知f(x)=x3﹣6x2+9x,
则f′(x)=3x2﹣12x+9=3(x﹣1)(x﹣3),………………………………………………8分
令f′(x)=0得x=1或3,
所以在(0,1)上f′(x)>0,f(x)单调递增,
在(1,3)上f′(x)<0,f(x)单调递减,
在(3,5)上f′(x)>0,f(x)单调递增,
在x=1处,f(x)取得极大值f(1)=4,在x=3处f(x)取得极小值f(3)=0,………..11分
又因为f(0)=0=f(3),f(5)=53﹣6×52+9×5=20>f(1),
所以f(x)在[0,5]上的最大值为20,最小值为0.……………………………………………13分
1
16.在(2√x- ) 6 的展开式中,求:
√x(1)求常数项,及此项的二项式系数;
(2)求奇数项的二项式系数的和;
(3)求系数绝对值最大的项.
1
【解答】解:展开式的通项公式为T =Cr (2√x) 6-r (- ) r= C r ⋅26-r ⋅(-1) rx3-r ,r=0,
r+1 6 √x 6
1,…,6,
………………………3分
(1) 由通项公式可得常数项为第4项即r=3时,为-160,……………….…………………….5分
其二项式系数为C 3=20;………………………………………………………………….…..7分
6
(2)奇数项的二项式系数和为25=32,………………………………………………………………..9分
(3)展开式的各项的系数的绝对值为S =C r ⋅26-r,r=0,1,…,6,
r+1 6
{Cr ⋅26-r≥Cr-1 ⋅27-r
设第r+1项的系数绝对值最大,则 6 6 ,…………………………………………11分
Cr ⋅26-r≥Cr+1 ⋅25-r
6 6
4 7
解得 ≤r≤ ,则r=2,………………………………………………………………………………..13分
3 3
所以系数的绝对值最大的项为T =C2 ⋅24 (-1) 2x=240x.…………………………………….……..15分
3 6
17.某市有一特色酒店由10座完全相同的帐篷构成(如图1).每座帐篷的体积为54 m3,且分上下两
层,其中上层是半径为r(r≥1)(单位:m)的半球体,下层是半径为r m,高为h m的圆柱体(如
π
图2).经测算,上层半球体部分每平方米建造费用为 2千元,下方圆柱体的侧面、隔层和地面三个
部分平均每平方米建造费用为 3千元设所有帐篷的总建造费用为 y千元.(提示:球体积公式:V=
4
πr3)
3
(1)求y关于r的函数解析式,并指出该函数的定义域;
(2)当半径r为何值时,所有帐篷的总建造费用最小,并求出最小值.
2 54 2
【解答】解:(1)由题意可得 πr3+πr2h=54π,所以h = - r,……….……………………..3
3 r2 3
分54 2 54
所以y=(2 r2×2+2 r2×3+2 rh×3)×10=100 r2+60 r•( - r),即y=60 ×(r2+ );
r2 3 r
π π π π π π
……….…….6分
54 2
因为r≥1,h>0,所以 - r>0,则1≤r<3√33,所以定义域为{r|1≤r<3√33},……….……..8分
r2 3
54
(2) 设f(r)=r2+ ,1≤r<3√33,
r
54
则f′(r)=2r - ,令f′(r)=0,解得r=3,……….………………….……………...10分
r2
当r [1,3)时,f′(r)<0,f(r)单调递减;
当r∈ (3,3√33)时,f′(r)>0,f(r)单调递增,
所以
∈
当r=3时,f(r)取极小值也是最小值,……….……..……….………………….……………...12分
且f(r) =27 , 总费用最小值为1620 ,……….……..……….…………………………………..14分
min
答:当半径r为3m时,建造费用最小,最小为1620 千元.……….……..……….…………….......15分
π π
π
2
18.甲、乙两位同学进行乒乓球比赛,经过大数据分析,每局比赛甲获胜的概率约为 ,乙获胜的概率约
3
1
为 .
3
(1)若比赛为三局两胜制,
(i)设比赛结束时比赛场次为X,求X的分布列与数学期望;
(ii)求乙最终获胜的概率;
(2)若比赛为五局三胜制,已知甲最终获胜了,求在此条件下进行了5局比赛的概率.
【解答】解:(1)(i)由题意可知,X所有可能的取值为2,3,……………………………………1分
2 2 1 2 5
则P(X=2)=( ) +( ) = ,………………………………………………………………………3分
3 3 9
2 1 4
P(X=3)=C1× × = ,…………………………………………………………………………5分
2 3 3 9
所以X的分布列为:
X 2 3
P 5 4
9 9
5 4 22
所以E(X)=2× +3× = ;…………………………………………………………………….7分
9 9 9
1 2 1 2 1 7
(ii)乙最终获胜的概率P=( ) +C1×( )×( )×( )= ;………………………………10分
3 2 3 3 3 27
(2)设事件A=“甲最终获胜”,事件B=“共进行了5场比赛”,
2 1 2 2 1 2 8 8 16 64
则P(A)=( ) 3+C1×( )×( ) 2× +C2×( ) 2×( ) 3= + + = ,……………13分
3 3 3 3 3 4 3 3 27 27 81 811 2 2 3 16
P(AB)=C2×( ) ×( ) = ,………………………………………………………..……………16分
4 3 3 81
16
P(AB) 81 1
故P(B|A)= = = .………………………………………………………………………17分
P(A) 64 4
8119.已知函数f(x)=ex﹣ax﹣1.
(1)当a=1时,求f(x)的单调区间与极值;
(2)讨论f(x)的单调性;
(3)当a=1时,设g(x)=f(x)﹣x2, 证明:g(x)在(0,+∞)上存在唯一的极小值点x
0,
3
且g(x )>- .(参考数据:e3≈20.09.)
0 4
【解答】解:(1)当a=1时,f(x)=ex﹣x﹣1,所以f′(x)=ex﹣1…………………1分
当x<0时,f′(x)<0;当x>0时,f′(x)>0,
所以f(x)在(﹣∞,0)上单调递减,在(0,+∞)上单调递增,…………………..…3分
所以当x=0时,函数f(x)有极小值f(0)=0,无极大值.…………………………….5分
(2)函数f(x)=ex﹣ax的定义域为R,f′(x)=ex﹣a.
对a进行讨论,分两种情况:
当a≤0时,f′(x)=ex﹣a>0恒成立,∴f(x)在R上单调递增;
当a>0时,由f′(x)>0,解得:x>lna;由f′(x)<0,解得:x<lna.
∴f(x)在(﹣∞,lna)上单调递减,(lna,+∞)上单调递增.
综上所述:当a≤0时,f(x)在R上单调递增;………………………………………… .7分
当a>0时,f(x)在(﹣∞,lna)上单调递减,(lna,+∞)上单调递增.…………….9分
(3) 当a=1时,g(x)=ex﹣x﹣1﹣x2,g'(x)=ex﹣2x﹣1,
令m(x)=ex﹣2x﹣1,则m'(x)=ex﹣2.……………………… ……………................….10分
当x (0,ln2)时,m(x)<0,m(x)单调递减;
当x (ln2,+∞)时,m(x)>0,m(x)单调递增,
∈
又因为m(ln2)=eln2﹣2ln2﹣1=1﹣2ln2<0,……………..................................................... .12分
∈
3
3
m(0)=0且m( )=e2-4>0,
2
3
所以存在唯一的x ∈(ln2, ),使得m(x )=0,即ex 0-2x -1=0①.………………..14分
0 2 0 0
当x (0,x )时,m(x)<0, 即g'(x)<0,g(x)单调递减,
0
当x∈ (x
0
,+∞)时,m(x)>0,即g'(x)>0,g(x)单调递增,
所以 ∈x
0
是 g(x)在(0,+∞)上唯一的极小值点.…….......................................................... .16分
3 3 3
则g(x )=ex 0-x -1-x2 ,由①可知g(x )=-x2+x >-( ) 2+ =- .………….....17分
0 0 0 0 0 0 2 2 4
声明:试题解析著作权属所有,未经书面同意,不得复制发布日期:2025/4/10 21:18:34;用户:郭静;邮箱:13961667196;学号:39485445