辽宁协作校2023-2024学年高三下学期三模数学试卷_2024年5月_01按日期_18号_2024届辽宁协作校高三下学期三模_辽宁协作校2023-2024学年高三下学期三模数学

姓名：__________________考生考号：__________________ 2023-2024 学年度下学期高三第三次模拟考试试题 数学 命题人：旅顺中学 王莹 沈阳二中 牛大伟 时间：120分钟 试卷满分：150分 注意事项： 1.答题前，考生务必将自己的姓名，准考证号填写在答题卡上。 2.答选择题时，选出每小题答案后，用铅笔把答题卡对应题目的答案标号涂黑。如需改动，用 橡皮擦干净后，再选涂其他答案标号。答非选择题时，将答案写在答题卡上。写在本试卷上 无效。 3.考试结束后，将本试卷和答题卡一并交回。 一、选择题：本题共 8小题，每小题 5 分，共 40 分.在每小题给出的四个选项中，只有一项是 符合题目要求的. 1．若全集U  R，A x|x2 ，B   y| y ex,xR  ，则下列关系正确的是（ ） A．A B B．B A C．BC A D．C A B U U 2．已知复数z在复平面上对应的点为 m,1 ，若iz 2，则实数m的值为（ ） A．0 B．1 C．1 D．1或1 3．已知正实数a，b，则“a2b2”是“a2 4b2 2”的（ ）条件. A．充分不必要 B．必要不充分 C．充分必要 D．既不充分也不必要   4．已知平面非零向量a，b满足 a  b ，且 2a 3b b，则 a,b （ ）    A． B． C． D．0 6 4 3 5．在调查对某大型活动满意度比例为0.9的人员中抽取10人，设当中持有满意态度的人数为X ，随机变 量Y 2X 3，则Y 的方差D  Y 的值为（ ） A．21 B．6.6 C．3.6 D．4.8 6．已知对数函数 f  x log x，函数 f  x 的图象上所有点的纵坐标不变，横坐标扩大为原来的3倍，得 a 到函数g  x 的图象，再将g  x 的图象向上平移2个单位长度，所得图象恰好与函数 f  x 的图象重合， 则a的值是（ ） 3 2 3 A． B． C． D． 3 2 3 3 学科网（北京）股份有限公司x2 y2 7．设点F ，F 分别为椭圆C:  1的左、右焦点，点P是椭圆C上任意一点，若使得PF PF m 1 2 8 4 1 2 成立的点P恰好有4个，则实数m的值可以是（ ） A．0 B．2 C．4 D．6 8．已知数列 a 中各项均为正数，且a2 a a  n1,2,3, ，给出下列四个结论： n n1 n1 n ①对任意的nN*，都有a 1 n ②数列 a 可能为常数列 n ③若0a 2，则当n2时，a a  2 1 1 n ④若a 2，则数列 a 为递减数列 1 n 其中正确结论有（ ）个 A．1 B．2 C．3 D．4 二、选择题：本题共 3小题，每小题 6分，共 18分.在每小题给出的选项中，有多项符合题目 要求.全部选对的得 6分，部分选对的得部分分，有选错的得 0分. 9．关于二项式 3x1 5的展开式，下列说法正确的是（ ） A．第三项系数为270 B．x2的系数为90 C．二项式系数和为25 D．系数和为25 10．已知max  x ,x , ,x 表示x ，x ， ，x 这n个数中最大的数.能说明命题“a，b，c，dR， 1 2 n 1 2 n max  a,b max  c,d max  a,b,c,d ”是假命题的对应的一组整数a，b，c，d 值的选项有（ ） ．．． A．1，2，3，4 B．3，1，7，5 C．8，1，2，3 D．5，3，0，1 11．已知双曲线C:x2 y2 1及直线l: y kx1，若l与C交于A，B两点，O是坐标原点，且△AOB 的面积为 2，则实数k的值可能为（ ） 3 5 6 A．0 B． C． D． 2 2 2 三、填空题：本题共 3小题，每小题 5分，共15分. 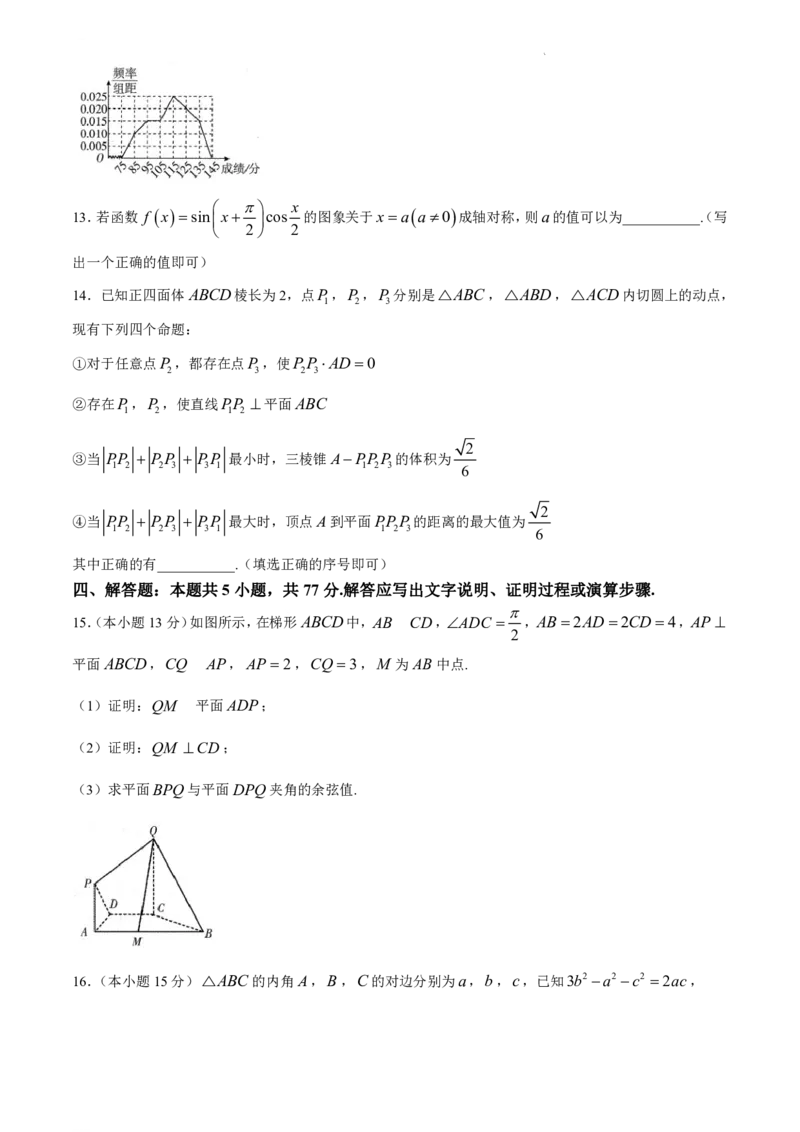12．某同学将全班某次数学考试的成绩整理成频率分布直方图后，将每个小矩形上方线段的中点连接起来， 并将小矩形擦去，得到频率分布折线图（如图所示）.已知该同学绘制频率分布直方图时确定的极差为60， 组距为10，据此估计此次考试成绩的平均数是___________. 学科网（北京）股份有限公司  x 13．若函数 f  x sinx cos 的图象关于xa  a0 成轴对称，则a的值可以为___________（. 写  2  2 出一个正确的值即可） 14．已知正四面体ABCD棱长为2，点P，P ，P 分别是△ABC，△ABD，△ACD内切圆上的动点， 1 2 3 现有下列四个命题： ①对于任意点P ，都存在点P ，使PP AD0 2 3 2 3 ②存在P，P ，使直线PP 平面ABC 1 2 1 2 2 ③当 PP  PP  PP 最小时，三棱锥APPP 的体积为 1 2 2 3 3 1 1 2 3 6 2 ④当 PP  PP  PP 最大时，顶点A到平面PPP 的距离的最大值为 1 2 2 3 3 1 1 2 3 6 其中正确的有___________.（填选正确的序号即可） 四、解答题：本题共 5小题，共 77分.解答应写出文字说明、证明过程或演算步骤.  15．（本小题13分）如图所示，在梯形ABCD中，AB CD，ADC  ，AB2AD2CD4，AP  2 平面ABCD，CQ AP，AP 2，CQ 3，M 为AB 中点. （1）证明：QM 平面ADP； （2）证明：QM CD； （3）求平面BPQ与平面DPQ夹角的余弦值. 16．（本小题15分）△ABC的内角A，B，C的对边分别为a，b，c，已知3b2 a2 c2 2ac， 学科网（北京）股份有限公司2 2CB  . 3 （1）求角B； 1 （2）若a2，设P，Q分别是边AB、BC上的动点（含端点），且S  S .当 PQ 取得最小 △BPQ 2 △ABC 值时，求点B到直线PQ的距离. 17．（本小题15分）已知函数 f  x  x  1eax  ，其在x1处的切线斜率为12e. （1）求a的值； （2）若点 m,n 在函数 f  x 的图象上，求 f  m  f  n 的取值范围. 18．（本小题17分）为进一步培养高中生数学学科核心素养，提高创造性思维和解决实际问题的能力，某 省举办高中生数学建模竞赛.现某市从M ，N 两个学校选拔学生组队参赛，M ，N 两个学校学生总数分 别为1989人、3012人.两校分别初选出4人、6人用于组队参赛，其中两校选拔的人中各有两人有比赛经验， 按照分层抽样从M ，N 两个学校初选人中共选择5名学生组队参赛，设该队5人中有参赛经验的人数为X . （1）求随机变量X 的分布列及数学期望E  X ； （2）各市确定5人组队参赛，此次比赛规则是：小组内自行指定一名同学起稿建立模型，之后每轮进行两 人单独交流.假设某队决定由A起稿建立模型，A从其他四名成员中选择一人B进行交流，结束后把成果交 由B，然后B再从其他包括A在内的四个成员中选择一人进行交流……每一个环节只能是两名成员单独交 流，每个小组有20次交流机会，最后再进入评委打分环节.现该市选定甲、乙、丙、丁、戊五人参赛，其中 1 甲、乙两人有参赛经验.在每次交流中，甲、乙被同伴选为交流对象的概率均为 ，丙、丁、戊被同伴选为 3 交流对象的概率相等，比赛由甲同学起稿建立模型. ①求该组第三次交流中甲被选择的概率； ②求第n次交流中甲被选择的概率 n20,nN  .  19．（本小题17分）设抛物线C的方程为 y2 4x，M 为直线l:xm  m0 上任意一点，过点M 作 抛物线C的两条切线MA，MB，切点分别为A，B（A点在第一象限）.  3 （1）当M 的坐标为 1, 时，求过M ，A，B三点的圆的方程；  2 （2）求证：直线AB 恒过定点； （3）当m变化时，试探究直线l上是否存在点M ，使△MAB为直角三角形，若存在，有几个这样的点， 说明理由；若不存在，也请说明理由. 学科网（北京）股份有限公司